基于离散演化映射的DC/DC变换器混合逻辑动态建模

段翔兮，佃松宜，郑万里

（四川大学电气信息学院，成都610065）

0 引 言

DC/DC变换器因其体积小、重量轻以及高效率和可靠性等优点，被广泛应用于数据传输与信息通信、航空航天、工业仪器、医疗设备、高压直流输电以及智能电网等领域，是电力电子技术研究的一个热点［1］。DC/DC变换器的建模是各项研究的基础，建立兼顾精确度和复杂度的模型是其分析设计的关键环节［2-4］。

离散时间模型已经成为DC/DC变换器非线性动力学分析和数字控制器设计的首选模型［5］。通常建模方法主要有状态空间平均法、精确离散映射和近似离散迭代映射，但分别有忽略了开关特性不能真实的反映其动态特性［6-7］；运算量非常大而难以适用于数字控制场合［8］；消去了矩阵指数和积分进行了大量近似，使得模型的动力学性质明显偏离了实际电路动力学行为的缺点［5］。离散演化映射建模方法基于哈密顿理论［9］，既保留了DC/DC变换器的动力学行为又兼顾了模型的精确度和复杂度［10］，目前此方法大多应用于机电系统，应用于开关功率变换器领域的建模分析非常少［11］，仅文献［9］采用拉格朗日力学变分积分建立了Boost电路的离散演化映射模型，模型计算量小、精确度高，但是未考虑DC/DC变换器的混杂特性。由于离散的开关动作，DC/DC变换器是一个典型的连续（或离散）时间状态变量和离散事件相互作用的混杂系统［12］。文献［13］采用ν步离散法建立了DC/DC变换器在CCM模式下的分段仿射模型；文献［14］对CCM模式下的Boost变换器进行了混合逻辑动态建模，但文献［13-14］都未建立系统在DCM模式下的模型，不能完整的描述系统的各个工作状态。文献［15］引入混杂动态系统和切换线性系统的概念，研究了PWM DC/DC变换器的能控性和能观性；文献［16］利用混杂系统理论对基本DC/DC电路在CCM和DCM工作模式下进行了建模，运用最小二乘法对模型进行参数辨识，但文献［15-16］建立的连续时间模型并未离散化，不适用于数字控制［8］。

本文将哈密顿原理和混杂系统理论有效的结合起来。针对Buck变换器，先依据哈密顿原理，采用变分积分器对其各个工作状态直接离散化，得到在CCM和DCM模式下的离散演化映射模型。然后基于混杂系统理论，将CCM和DCM模式统一起来，建立了Buck变换器的混合逻辑动态模型，以描述系统的动态特性、切换规律和约束关系。

1 离散变分原理和混合逻辑动态系统

1.1 离散变分原理

离散变分原理的主要思想来源于处理力学的变分性质，在离散化的情况下保持这种变结构，并以一阶（或更高阶）直接离散化欧拉-拉格朗日方程。变分原理可以很容易的从连续的拉格朗日函数得到离散化的欧拉-拉格朗日方程［17］。

1.2 混合逻辑动态系统

MLD理论是一种应用于混杂系统建模的重要理论，主要思想是通过计算逻辑变量和混杂系统的约束构成不等式，从而确定系统的工作状态。它能描述诸如分段仿射系统、约束线性系统、有限状态机等一大类系统［18］。混杂系统的通用MLD模型如图1所示，图1中的MLD模型统一描述了连续时间动力学系统和离散事件动力学系统，并通过数字—模拟（D/A）和模拟—数字（A/D）两类接口获得不同动力学系统间的相互联系。其中Xc、δo、δi等都是设定的辅助逻辑变量，在模型中采用布尔量进行表示，Zi为辅助变量。

2 Buck变换器的离散演化映射模型

2.1 Buck变换器的工作模态

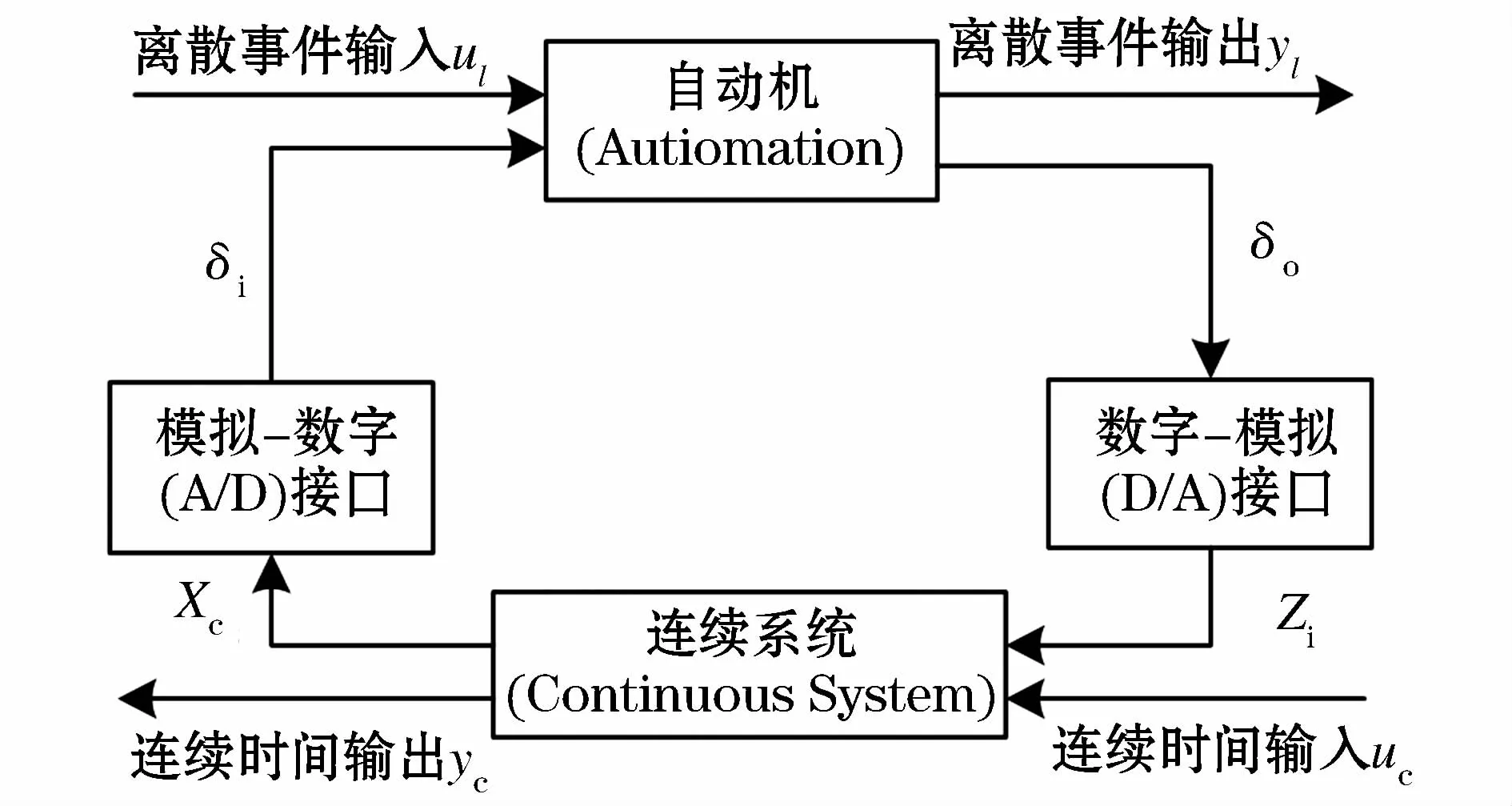
图1 通用MLD模型Fig.1 General MLD model

根据Buck变换器电感电流的连续和断续情况，工作模式可分为连续模式（CCM）和断续模式（DCM）。工作在DCM时分为三种模态（模态1～模态3），工作在CCM时只有两种模态（模态1～模态2），各个工作模态的等效电路如图2所示。

图2 Buck变换器及其等效电路图Fig.2 Buck converter and its equivalent circuit diagram

2.2 在CCM模式下Buck变换器的离散演化映射模型

在开关功率变换器系统中，首先需要确定一个合适的初始开关位置参数u（即工作模态），u=0时，开关管闭合，u=1时，开关管关断。然后分别定义Tu和Vu为电路系统的动能和势能。用Fu表示电路的瑞利耗散函数，Vu，nc为非保守的势函数［17］。对于Buck变换器，可得到以下表达式：

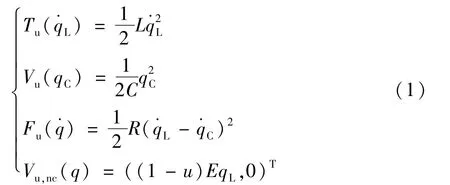
式中qL为电感中的循环电荷；qC为存储在输出电容中的电荷分别为电感电流和电容电流；常数参数L为电感；C为电容；R为负载电阻值；E为直流电源值，一个非保守的拉格朗日函数定义如下：

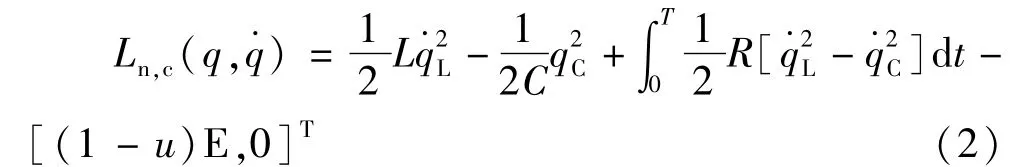
式中Ln，c是指保守的拉格朗日函数。运用参数法离散拉格朗日函数，可得离散的保守拉格朗日函数：

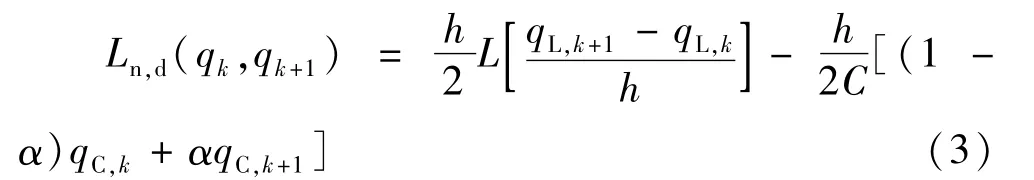
非保守力项表示为：

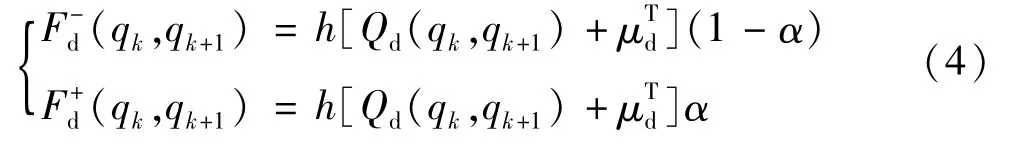
采用单点正交法则近似，最终耗散力可表示为：

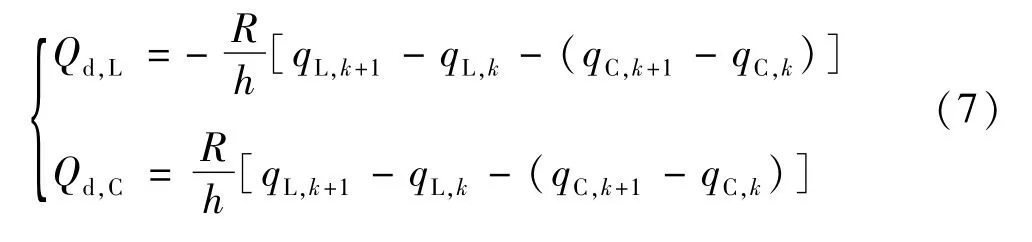
选取自由参数α=1/2（即中点法则单步积分子），位置的迭代计算规则如下式所示：

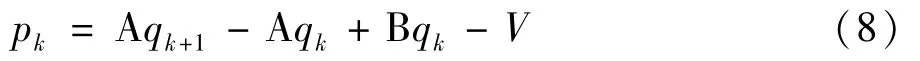
其中 pk=（pL，k，pC，k）T和 qk=（qL，k，qC，k）T，此外

根据式（8）首先获得qk+1的迭代表达式：

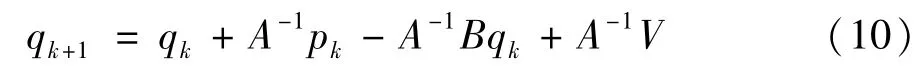
最终得到qk+1的标量形式：

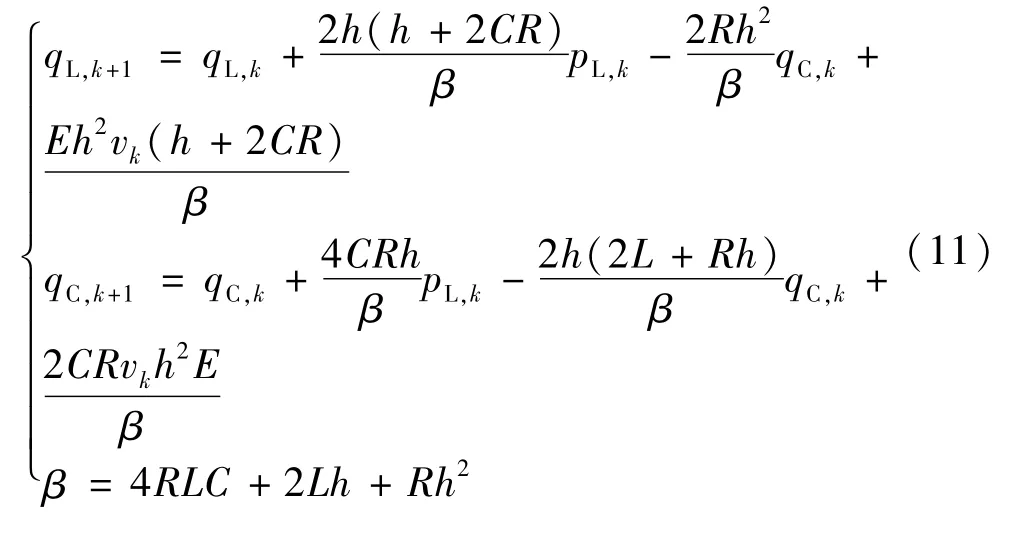
式中vk=1-uk，表示开关位置参数。下一时刻的动量方程表达式进行更新：

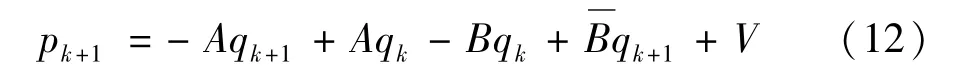
那么，通过计算（12）式，动量方程的迭代规则可表示如下：

在Buck变换器的离散演化映射模型中，第一个状态变量为电感中的循环电荷qL，则输入电流表示为第二个状态变量被定义为输出电容的电压，表示为x2=qC/C。最终，得到Buck变换器离散演化映射模型，其中 x1，k+1=pL，k+1，x2，k+1=qC，k+1，x1，k=pL，k为输入电流，x2，k=qC，k为输出电容电压。模型如下：

2.3 在DCM模式下Buck变换器的离散演化映射模型

在DCM模式下，对于Buck变换器可得以下表达式：

按上述步骤计算得到Buck变换器在DCM模式下的离散演化映射模型：

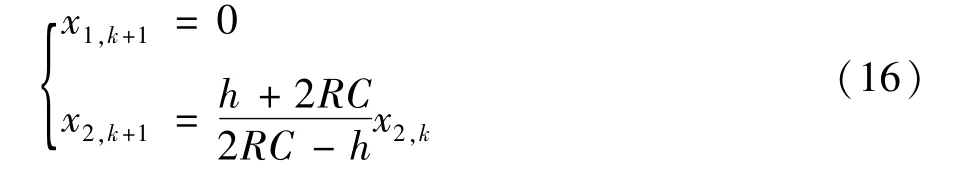
3 基于离散演化映射的MLD模型

在MLD理论的框架下，模型包含动力学系统的所有运行模态，xk+1=Aaxk+BaE为三种不同模态下的系数模型表达式，a=1，2，3表示模态1，2，3。各状态量沿用之前定义，系数矩阵为：

ul∈{0，1}，当ul为1时，开关管处于闭合状态，当ul为0时，开关管处于断开状态。通过前面对Buck变换器的运行机制分析可知，当变换器工作于DCM状态时，电感电流幅值不大于0，则可推导只有当ul＾iL≤0=1满足时，变换器才工作于DCM状态，则得到Buck变换器的混杂自动机模型（见图3）。

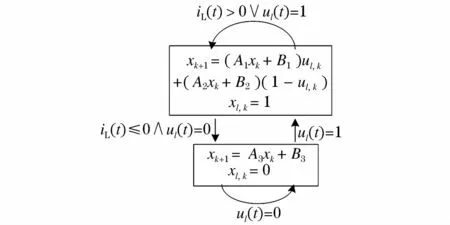
图3 Buck变换器的混杂自动机模型Fig.3 Hybrid automata model of a Buck converter

为了简单起见，定义辅助逻辑变量xl∈{0，1}。当为0时，表示开关管处于关断状态且电感电流幅值不大于0，当为1时，表示开关管处于闭合状态或电感电流幅值大于0。基于上述定义，为便于构造MLD模型，可先将变换器的动力学系统模型在分段仿射理论的框架下进行描述：

将iL≤0状态转化为布尔量进行描述，定义δ1，k∈{0，1}，表示：

这一定义的功能，类似前面所述的模拟-数字（A/D）端口的运行机理。δ1，k同图 1中的布尔量 δi相同。自动切换规则可以全部依靠逻辑变量进行定义：

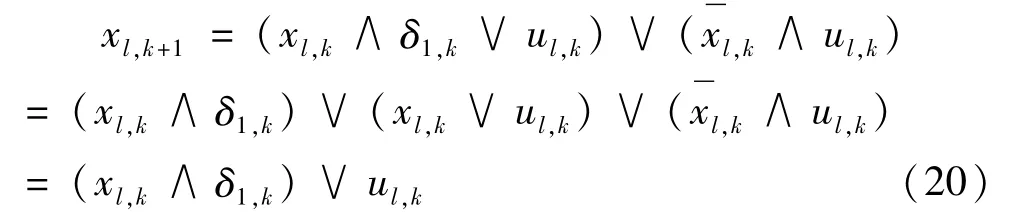
将式（20）转化成线性的表述形式，定义一个新的辅助逻辑变量 δ2∈{0，1}，δ2，k=1↔xl，k=1∧δ1，k=1被改写为 xl，k+1=δ2，k∨ul，k。延续同样的方法，定义新的辅助逻辑变量 δ3∈{0，1}，δ3，k=δ2，k∨ul，k，最终得到 xl，k+1的线性表述形式：xl，k+1=δ3，k。但 δ2，k与 xl，k和δ1，k间的关系仍然是非线性，可用下述不等式组将其转化为线性形式描述：

同样的思路，得到 δ3，k同 δ1，k和 vl，k的线性关系：

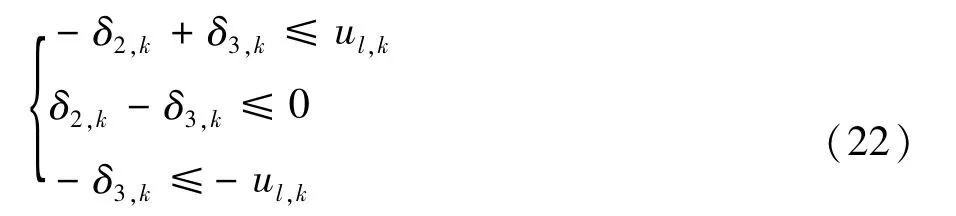
将新定义的辅助逻辑变量代入式（18），得到：

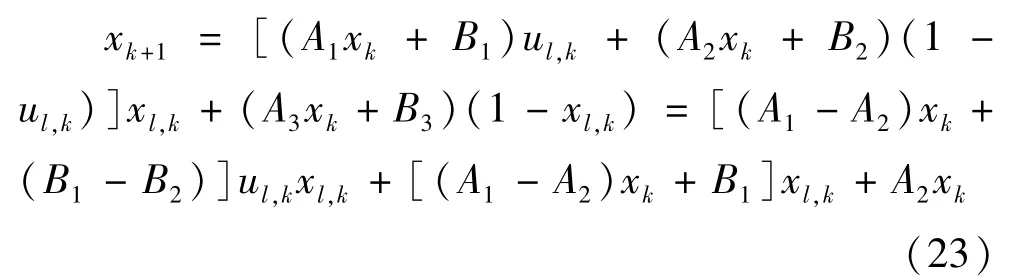
但式（23）又产生了 ul，kxl，k这组非线性形式，因此定义辅助逻辑变量 δ4∈{0，1}，δ4，k=ul，kxl，k，则可得到线性的不等式组：

为了表示图1中的数字-模拟（D/A）模块，定义新的辅助变量z1和z2：

综合式（23）和式（25），可得到如下表达式：

式（26）中描述了图1中的连续动力学系统模块。考虑到变换器实际运行中对输入状态量和输出状态量的限制，可将（25）中非线性的表达式转化为线性的混合整数不等式组：

式中 Mzi和 mzi，其中 i∈{1，2}，表示 zi的最大和最小值。通过上述步骤，将式（21）的分段仿射系统形式转化为式（27）的带有约束的线性系统形式。根据MLD理论，将系统的动力学模型表示为：

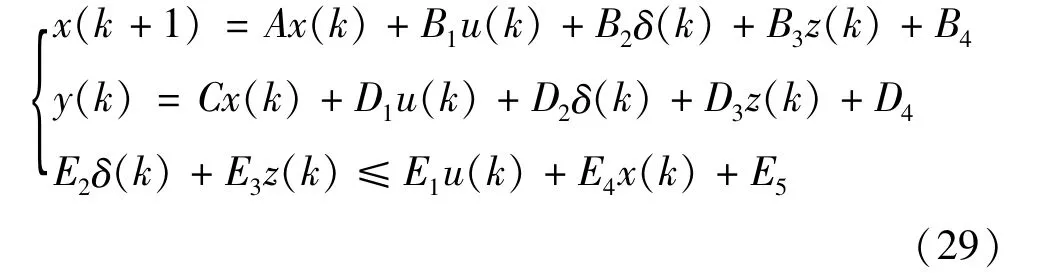
通过给定状态变量xk和逻辑变量Uk的初始状态，计算不等式组求得辅助逻辑变量δk和辅助变量Zk，确定工作模态，更新xk+1和yk输出，到此，完成一个采样周期的迭代运算。

4 仿真结果及分析

基于Matlab软件搭建模拟电路，仿真参数的设置为输入 DC 50 V，电感 L=0.05 H，电容 C=680μF，负载R=23Ω，采样时间h为10μs，开关周期Ts为10μs，采集电感电流和输出电压作为状态量。将Buck变换器的MLD模型同模拟电路进行对比，采用开环仿真验证模型的正确性。MLD模型和近似离散迭代模型采用m程序基于C语言进行编写，并进行对比，分析模型的精确度。

在0.2 s的时间内，实际电路、近似离散模型和基于演化映射的MLD模型的电感电流的波形如图4所示。

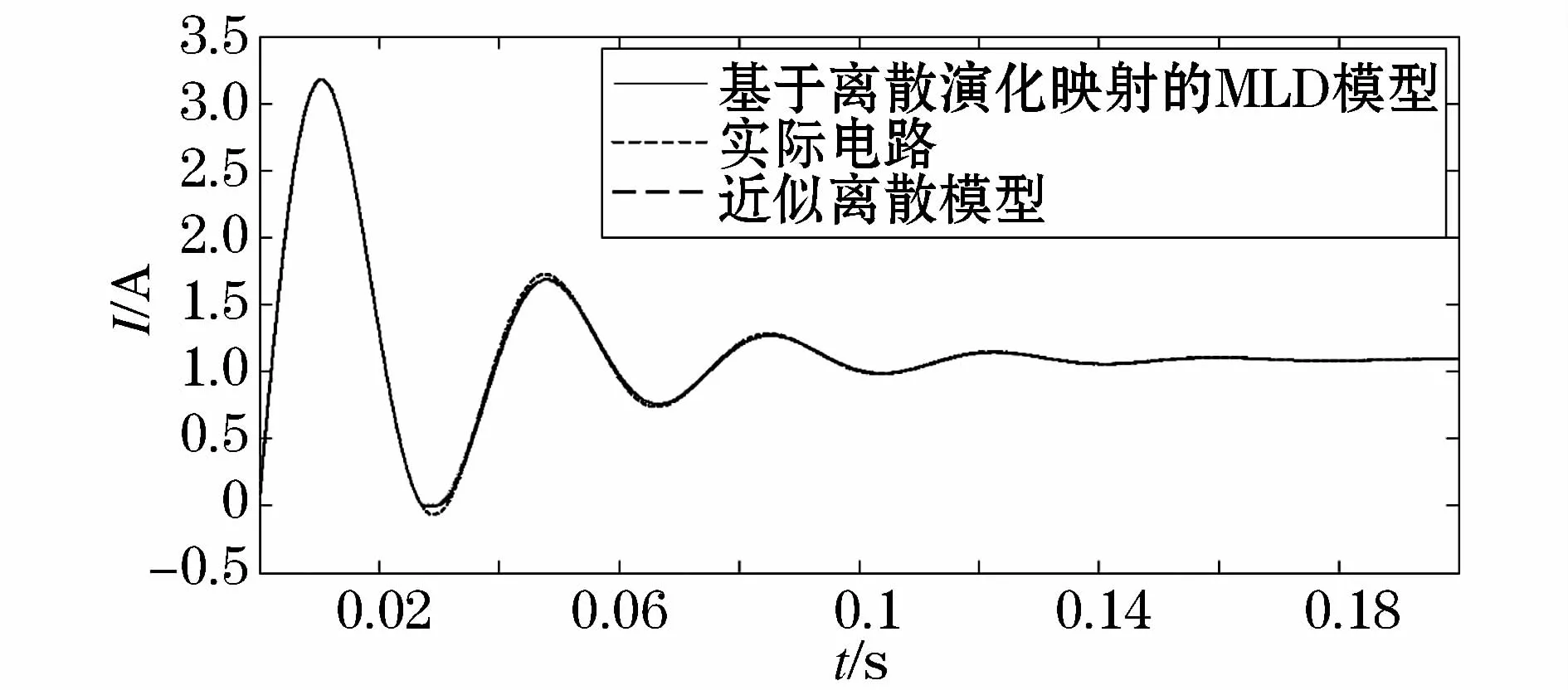
图4 电感电流对比Fig.4 Inductor current in contrast

通过对电感电流不稳定状态下的输出波形放大得到如图5所示的波形。

图5 电感电流局部放大对比Fig.5 Inductor current zoom in contrast

当电感电流等于0时，变换器进入DCM模式，对进入DCM模式的区域放大，如图6所示。

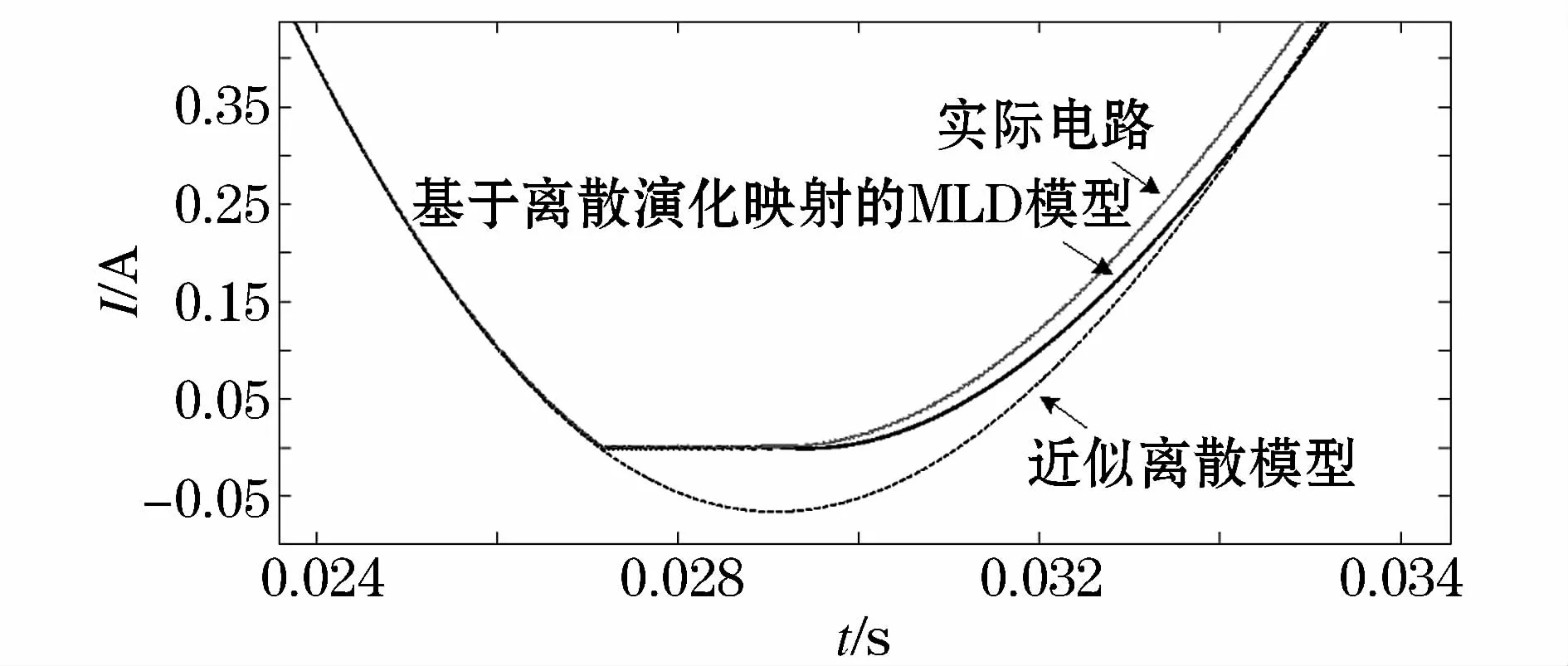
图6 进入DCM模式时电感电流放大对比Fig.6 Inductor current zoom in contrast in DCM

当系统进入稳定状态时，电感电流的输出波形如图7所示。

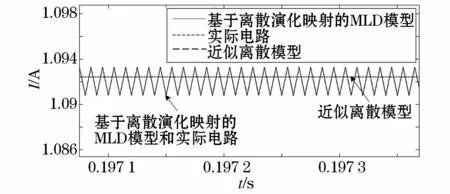
图7 稳态下电感电流放大对比Fig.7 Inductor current of steady-state zoom in contrast

在0.2 s的时间内，实际电路、近似离散模型和基于演化映射的MLD模型的输出电压波形如图8所示。

通过对输出电压不稳定状态下的波形放大得到如图9所示的波形，对稳定状态下的输出电压波形放大见图10。

仿真结果分析：

（1）通过与实际电路的电感电流和输出电压进行对比，可得所建立的基于离散演化映射的MLD模型是正确的；

图8 输出电压对比Fig.8 Output voltage in contrast

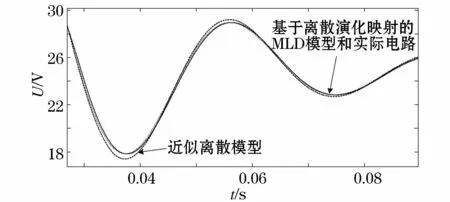
图9 输出电压局部放大对比Fig.9 Output voltage partial zoom in contrast

图10 稳态下输出电压局部放大对比Fig.10 Output voltage of the steady-state partial zoom in contrast

（2）模型复杂度明显小于精确离散映射模型，计算量小；

（3）相比于近似离散迭代模型，MLD模型与实际电路电流和电压更加接近，精确度更高；

（4）从图6可以看出，当电感电流等于0时，变换器进入DCM模式，此时近似离散模型明显偏离实际电路，而MLD模型能够很好的跟踪实际电路的电感电流，完整的描述了系统的各个工作模态；

（5）实际电路中电感充放电导致电流波动等原因形成高频纹波，这一现象为DC/DC变换器固有的高频动态特性。从图7可以看出，MLD模型保留了DC/DC变换器固有的高频动态特性，完整的反映了稳态下电流高频纹波的幅值与频率；

（6）通过局部放大图10可以看出，MLD模型与实际电路的输出电压信号的跟踪精度达到了小数点后4位。

5 结束语

针对Buck变换器，先依据哈密顿原理，采用变分积分器对其直接离散化，得到在CCM和DCM模式下的离散演化映射模型。然后基于混杂系统理论，将CCM和DCM模式统一起来，建立了Buck变换器的MLD模型。通过仿真验证和分析，证明了该方法的有效性，模型完整的描述了系统的各个工作状态。与精确离散模型和近似离散模型相比，基于离散演化映射的MLD模型计算量小且精确度高，还反映了稳态下电感电流纹波这一动态特性。基于离散演化映射的MLD模型的建立为下一步变换器的非线性动力学行为分析和数字控制器的设计做好了铺垫。