基于扩展相分量法的OPGW系统接地短路电流计算
2017-12-20钟成苏汉金志杰杜帅兵
钟成,苏汉,金志杰,杜帅兵
(1.国网河北省电力公司,石家庄050021;2.国网河北省电力公司衡水供电公司,河北衡水053000)
0 引 言
我国大部分110 kV及以上电压等级的架空输电线路采用双OPGW线配置,目前的趋势是用光纤复合OPGW线逐步代替普通地线。相较于传统地线而言,光纤复合OPGW线阻抗值更小,故障时,短路电流通过其分流的比例更大。架空输电线路可以分解为由档距为单位形成的大规模电力网络。所形成的大规模的电力网络需要考虑的因素很多,从相导线角度来看的话,包括架空输电线路的换位信息和线路两侧系统的参数等;从OPGW线的角度来看的话,包括OPGW是否逐塔接地运行,是否分段绝缘运行和是否经阻抗接地等多种运行方式等情形;从电力杆塔的角度来看的话,包括杆塔的级数、杆塔的型号和杆塔接地电阻等参数;进一步还包括相线和OPGW线之间、各OPGW线之间的互感影响等。这些都从一定程度上造成了线路运行状况的复杂化[1-5]。
通过广泛的调研发现,为了计算发生单相接地时短路电流在OPGW线上的分布,目前存在以下三种方法[6-12]:采用简化计算方法时,没有考虑相线和OPGW线之间的磁耦合作用,也未不考虑架空输电线路的运行方式,OPGW线上的短路电流以线路出口变电站母线短路电流的一定百分比分流,此百分比多是基于工程经验。此种方法虽然简单,但是忽略的重要因素太多,导致计算结果粗糙,可信度较低。有研究者采用序分量法计算,但是序分量法应用的一个重要前提是系统的三相参数对称,实际线路运行状况复杂,对称的条件更难满足,导致计算结果保守。基于相分量的计算方法则能充分反映出输电线路的复杂运行状况,对三相系统参数对称性没有要求,导线之间的互感、架空地线的不同运行方式等因素均能体现。因此,面对线路和架空地线复杂的运行方式,相分量法在计算架空地线上短路电流的应用中越来越广泛。文章在传统相分量法的基础上,并对其进行了改进,采用扩展相分量法,即将相导线和OPGW线作为一个整体,同时考虑两者之间的相互作用,将相导线和OPGW线在分析模型上采用一致的模型来进行分析。
通过该模型对短路电流分布情况进行量化计算和EMTP算例验证,对比验证了文章计算结果的正确性。最后,应用文中的扩展相分量模型对某条220 kV的实际线路进行计算,得到OPGW线每级档距上的短路电流,并总结其分布规律。这有助于实际工程中对OPGW线的选型和校验。
1 架空输电线路扩展相分量法模型
图1所示为架空输电线路的运行示意图。图中展示了由三相输电导线和两条OPGW线组成的系统。下面对图中参数的具体含义进行逐一表述:Ea,Eb分别表示OPGW线上的感应电动势,用Za,Zb分别表示OPGW线的自阻抗,用Ia,Ib分别表示OPGW线上的分布的电流。为了反映出OPGW线在水平方向和垂直方向上的运行方式,文章用部分有特定含义的电阻进行表示。在水平方向上,用电阻r1,r2来表示OPGW线是否处于分段绝缘的运行方式;在垂直方向上,用k1,k2来表示OPGW线在杆塔处的接地方式,具体有包括逐塔接地的方式和单点接地的方式。对r1,r2,k1,k2的值进行设置就能反映出其具体复杂的运行方式,当 r1,r2,k1,k2的值为0时,即认为连接和接地,当 r1,r2,k1,k2的值为无穷大时,即认为不连接和不接地。Fault表示发生接地短路点。
下面将介绍基于扩展相分量法的数学计算模型。将架空输电线路的电源和线路的数学模型连接起来,并将图1中的各级档距上的阻抗进行矩阵化表示,就能得到完整的考虑OPGW线的架空输电线路模型,假设线路一共有n档,如图2所示。
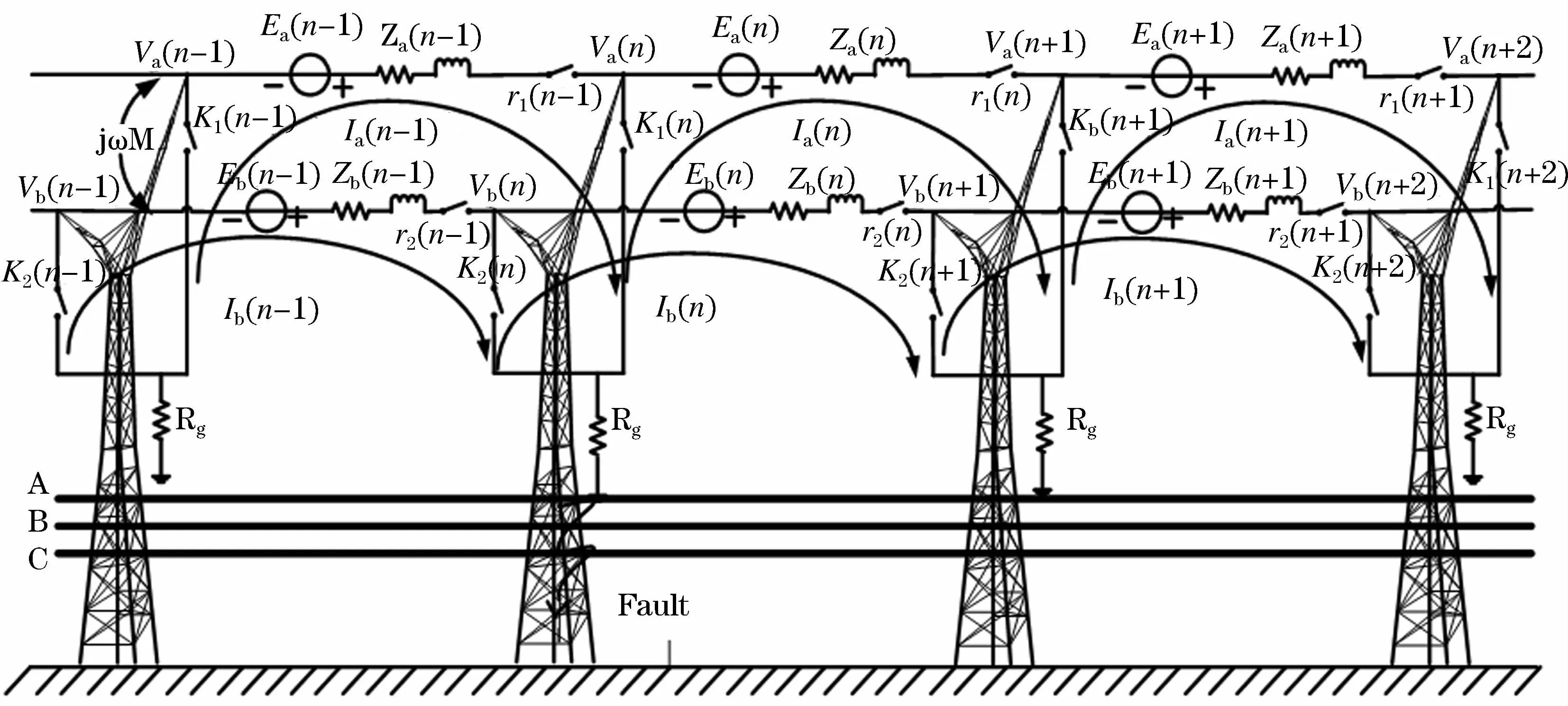
图1 线路运行示意图Fig.1 Schematic diagram of transmission line operation
为了方便分析,对全线上每级档距进行编号。设定电源所在的那一级档距为第1级,线路中的第k级档距上的纵向电压源用Ek来表示。用Eeq来表示线路电源的等效的电动势矩阵。当该级档距不是连接电源,或者该级网孔为负荷时,不难得到Ei=0(i≠1);当该级档距连接的是线路的终端电源时,不难得到E1=Eeq,Zdo=Zeq。进一步,根据基尔霍夫电压定律,在每级档距上,能够列写出相关的网孔回路方程:
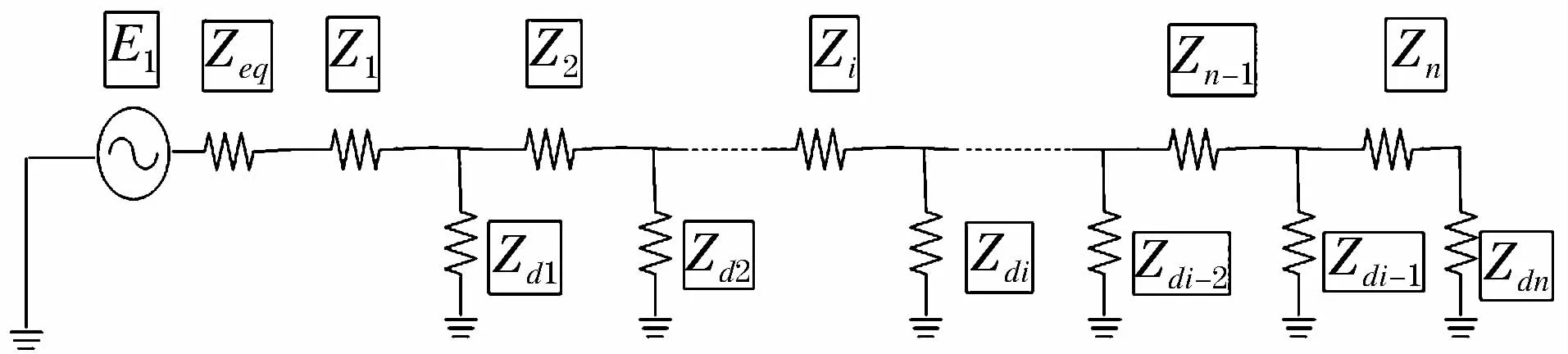
图2 架空输电线路扩展相分量法计算模型Fig.2 Calculation model of the improved phase componentmethod in OPGM

写成矩阵:

式(2)中,I的含义为:

式(2)中,E的含义为:
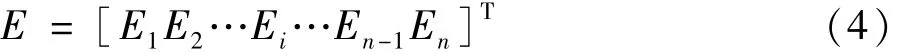
下面对式(2)~式(4)中相关的矩阵进行解释。式中I表示的是纵向电流,其中的元素Ii是一个块矩阵。Ii的矩阵规模为y×1的列向量,是由第i级档距上的电流组成;上式中的E表示的整条输电线路上的纵向电压块矩阵。Ei的矩阵规模是大小为y×1的列向量,是由第i级档距上的各条导线上的纵向电压组成。需要说明的是,除了和电源相连的档距上的纵向电压中Ei不是一个元素全为0的矩阵,在整条输电线路其他档距上的纵向电压是一个元素全为0的矩阵。
其中Z是块三对角矩阵,即:
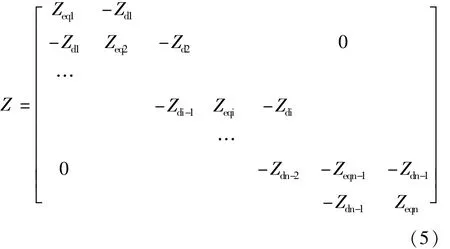
式中 Zeqi=Zdi-1+Zi+Zdi(1≤i≤n)。
由以上的分析不难得到,如果整条输电线路的档距级数是n的话,那么Z就是一个矩阵规模为y×n的块三角矩阵。在比较普遍的情况下,一条输电线路的档距级数可能在数十级甚至能够达到数百级的规模。这时,该块三角矩阵的阶数就会是一个比较大的情况。如果使用Gauss消去法来进行处理上述方程组的话,整体的计算效率和速度都不会很快。但是可以应用“追赶法”对其进行求解。因为,该块三角矩阵有高度稀疏,并且是对角占优的特点。
我们注意到,“追赶法”对块三角矩阵的化简可以很大程度上提高计算速度和计算效率,因为其对运算次数的减少效果显著,是解决大型矩阵很好的方法[13-14]。正如上文所述,对求解文中所提到的应用扩展相分量法来计算OPGW线上短路电流分布的求解具有很好的适应度。
下面将介绍将块三角矩阵进行“追赶法”分解的步骤,将该块三角矩阵进行LU分解后,其中L和U的表达式如下:

式中 Gi、Di、Pi皆是 y×y阶的子矩阵;Oi是 y×y阶的单位矩阵。原方程可以写成:

用待定系数法可以确定L和U中的非零元素。
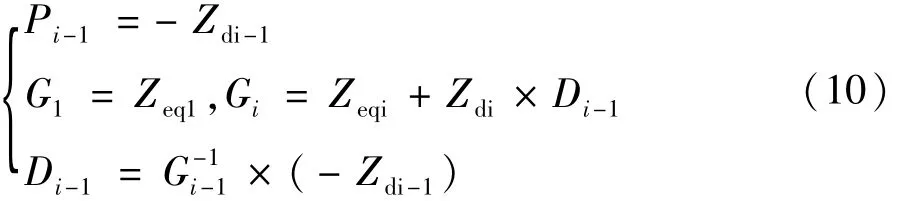
式中 i=2,3,…,n。
所以有:
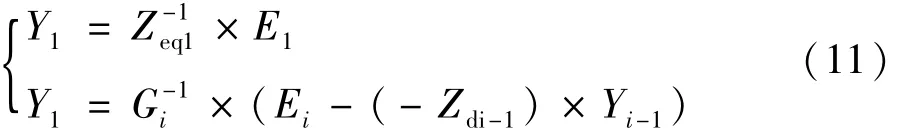
式中 i=2,3,…,n。
再由Y=UI求得:

式中 i=n-1,n-2,…,1。
随着i从1到n的变化,式(11)中Yi展示的是块三角矩阵从小到大的求解过程,其对应着“追赶法”的“追”过程;随着i从n到1的变化,式(12)中E′i展示的是块三角矩阵从大到小的求解过程,其对应着“追赶法”的“赶”过程。通过上述的求解,我们不难得到:

架空输电线路每一级档距上的短路电流的分布都能通过以上的求解过程进行计算。
2 算例验证
某电网110 kV单回线双端电源输电线路的结构示意图如图3所示。该架空输电线路全线长10 km,共35级杆塔,每级档距取平均值0.3 km,相关参数已在图3中标示。

图3 线路结构示意图Fig.3 Structure schematic diagram of transmission line
在输电线路发生接地短路后,故障相线上的短路电流容易得到,但是在OPGW线上的短路电流几乎没有进行过相关测量。为了验证计算结果的正确性,文章将上述算例的计算结果和电力系统仿真软件EMTP的仿真结果进行对比。EMTP是行业内认可度很高的故障分析软件,EMTP的仿真模型中元件参数均和算例保持一致。需要说明的是,文章基于相分量模型的计算结果时故障后短路电流的稳态值,取EMTP仿真结果的稳态值与其比较,从而达到验证的目的。
下面对建立EMTP仿真模型时的注意点进行说明。EMTP模型中的单相接地短路故障发生器由分相元件、开关和接地电阻组成,0.1 s时开关闭合,模拟A相发生接地短路,1 s后开关断开,故障消除。这样设置保证了足够的时间得到发生接地短路后的电流数据,短路电流采用电流元件进行监测。LCC线路模块能够自定义相线和OPGW线的数目,通过对该模块参数的设置,仿真模型中各导线之间互感的作用能够很好地体现,1个LCC模块表示1级档距。图4所示的是线路元件LCC模块参数设置第一部分,采用5导线模型,即三相单回线和两条OPGW线,根据算例实际情况,线路是否换位、大地电阻率、档距长度等可在此设置。
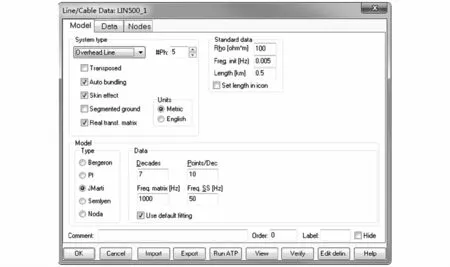
图4 线路LCC模块参数设置1Fig.4 Parameter setting part of LCC 1
图5所示的是LCC模块参数设置第二部分,此部分影响重大。根据相线和OPGW线的型号、线路的实际塔型设置元件的参数。其中,三相导线编号依次为1~3,OPGW编号为4,JBL编号为5;Rout表示导线的半径;Resis表示导线单位长度的直流电阻值;Horiz表示以中间相为参考时的水平距离;Vtower表示导线在杆塔处的垂直距离;Vmid表示导线在档距中央是的垂直距离;Separ表示分裂导线之间的距离;NB表示导线分裂数。为保证仿真结果的准确性,所有的参数均需进行正确的设置。点击View后能够对设置的塔型进行预览,顶部是两条OPGW线,下方是三条相导线,同时和塔型CAD图进行校准。每档的OPGW线和相线上的电流均采用电流元件进行监测,采集故障后的数据。

图5 线路LCC模块参数设置2Fig.5 Parameter setting part of LCC 2
当在输电线路的中部5 km,即18号档距处发生单相接地短路时,A相的短路电流计算结果如表1所示,短路点的短路电流由两端电源提供,分别见表1中的S侧提供的短路电流和M侧提供的短路电流。从表1中能够看出,对于本算例中的双端电源线路,EMTP仿真结果和文中计算结果在一个比较理想的范围内,相差0.5%左右。说明了基于文中计算方法得到的相线上接地短路电流的分布是可靠的。

表1 单相接地短路电流的比较Tab.1 Comparison of single-phase to ground fault current
进一步对OPGW线上的电流分布情况进行验证,由于OPGW线的逐塔接地,使得全线每级档距段的OPGW线上电流值也不相同。表2表示仿真和文中计算得到的光纤复合OPGW线OPGW和普通OPGW线JLB上短路电流。
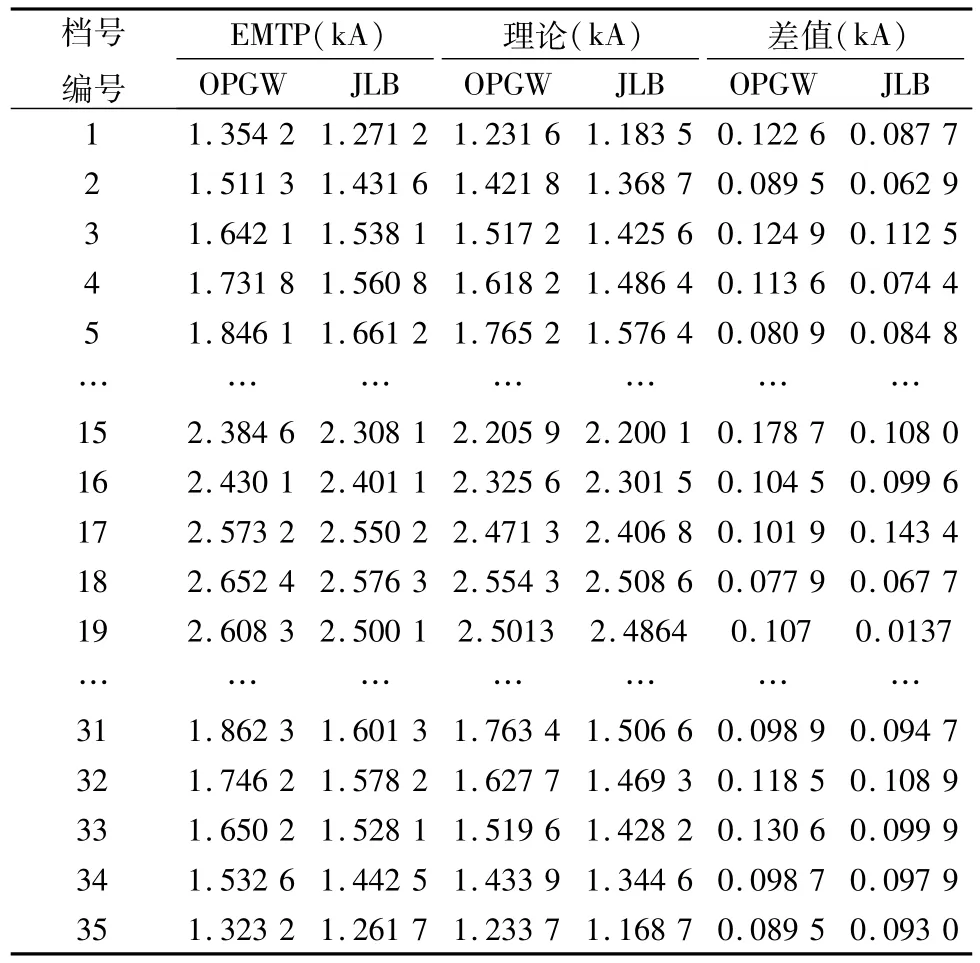
表2 OPGW和JLB每档上电流的比较Tab.2 The comparison of current on OPGW and JLB
通过对OPGW线和JLB两条OPGW线,EMTP和计算结果的对比发现:在发生短路的18号档距处,档距上的短路电流相差不大,差值分别为0.077 9 kA和0.067 7 kA。随着从短路点到线路首末两端档距的推移,仿真结果和计算结果的差值变大,但在可接受的范围内。两者误差产生的原因在于计算时两条OPGW线之间的互感影响也考虑了进来,但在LCC模块中只有相线对OPGW线的影响。注意到,在短路点附近档距上导线短路电流是全线档距中最大的,对OPGW线的挑战最为严峻,和EMTP仿真差别不大可说明文章提出的计算方法得到的结果是可靠的。综合以上分析,EMTP仿真结果和文中的计算结果在相线和OPGW线上短路电流的分布情况都有很好的吻合,从而验证了文章算法的正确性。
需要说明的是,若只用EMTP进行仿真,面对输电线路的几十级甚至上百级杆塔,需要对每级杆塔和各导线参数都要进行繁琐的设置,才能得到准确的仿真结果,计算时间和成本不容忽视[15]。依托文中计算方法的而开发架空输电线路单相接地短路电气量分布计算软件,计算中可设定塔型后调用,和EMTP相比较,计算效率显著提升,并已在相关工程项目中应用。
3 实际线路上的应用
某110 kV线路单回线运行,线路长度为7.8 km,导线为 JL/G1A-400/35-48/7钢芯铝绞线,单位长度电抗为0.416Ω/km,架空地线为OPGW-24B1-100,OPGW线电抗为0.216Ω/km。
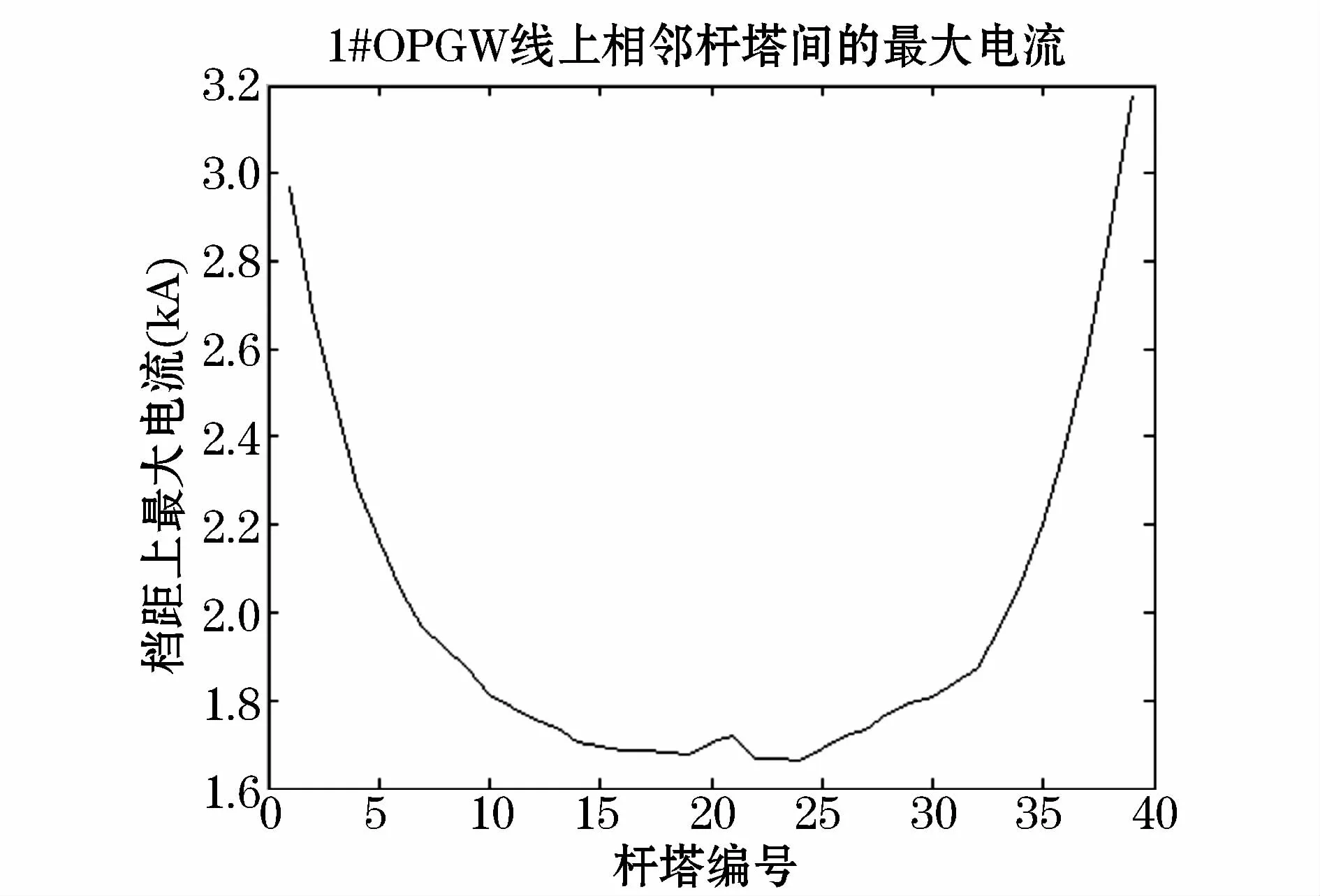
图6 线路逐塔短路时1#OPGW线上电流分布Fig.6 Fault current distribution on OPGW1
逐塔故障时,1#OPGW线上的最大电流分布如图6所示,2#OPGW线上的最大电流分布如图7所示。根据图6和图7,可以对OPGW线上短路电流的分布情况进行分析。随着发生接地短路的杆塔从线路首端向线路末端变化,OPGW线上最大短路电流也逐渐经历从一个最大值向最小值分布的过程。这与线路两端电源的供流有关,同时在发生接地短路的杆塔处的相邻档距上OPGW线的短路电流必然最大,在此处应考虑对OPGW线的分流水平。对每一级档距OPGW线短路电流的校验需要重点考虑与该级档距相连的杆塔处发生接地短路,此种状况是考验最为严峻的情形。
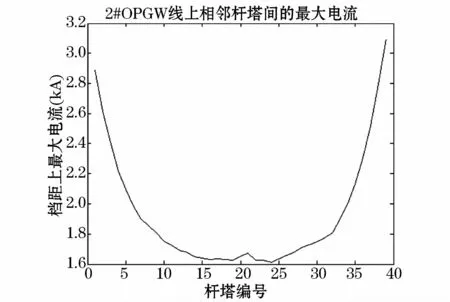
图7 逐塔短路时2#OPGW线上电流分布Fig.7 The fault current distribution on OPGW2
4 结束语
文章针对架空输电系统的单相接地短路故障,充分考虑了三相导线和双OPGW线的复杂运行方式,更适用于双端电源、双OPGW线和多相线配置的输电线路上发生单相接地短路时,短路电流在OPGW线中的分布计算。利用上述方法,也能计算出发生单相接地短路时,OPGW线的分流系数。基于文中方法而开发出的计算软件,已经在实际工程中应用,取得了良好的工程效应,能够得出文章的研究内容在变电站设计,输电线路的建设等工程实际中有重要意义的结论。
