磁性元件近场磁耦合仿真分析

，，

(国网福建省电力有限公司漳州供电公司，福建 漳州 363000)

磁性元件近场磁耦合仿真分析

胡钦俊，陈婉纯，黄靖

(国网福建省电力有限公司漳州供电公司，福建 漳州 363000)

磁性元件如电感、共模电感、变压器等均是功率变换器中的重要组成部分，它们的摆放位置与布线方式都有可能影响其对电磁干扰噪声的抑制作用。由于功率变换器越来越小型化，高功率密度化，其元器件放置都十分紧凑，各元器件间存在着近场耦合效应。本文分析了磁性元件间近场磁耦合机理并通过实验来验证仿真所得到的磁性元件间近场磁耦合参数的准确性。

磁性元件;磁耦合;仿真

1 引言

磁性元件如电感、共模电感、变压器等均是功率变换器中的重要组成部分，它们的摆放位置与布线方式都有可能影响其对电磁干扰噪声的抑制作用。由于功率变换器越来越小型化，高功率密度化，其元器件放置都十分紧凑，各元器件间存在着近场耦合效应[1-4]。近场耦合主要分为磁场耦合与电场耦合，而磁性元件间的耦合方式主要以磁场耦合为主，主要是表现在共模电感之间、共模电感与电容回路的寄生电感之间以及共模电感与主电路其它磁性元件之间[5-8]。

2 磁性元件的外部磁场分析

磁性元件在空间中漏磁场的交链是各元件间存在近场磁场耦合的主要原因，本节通过三维电磁场仿真软件HFSS分析了共模电感、变压器的磁性元件在空间的磁场分布情况及对其他磁性元件的影响。

2.1 共模电感器共模电感分量磁场分布

图2是根据某实际共模电感的尺寸(如图1所示)进行建模的HFSS三维仿真模型图，其中黄色部分为绕组，灰色部分为铁氧体磁环，通过对共模电感设置方向相同的电流激励并进行仿真来得到共模电感周围的磁场分布，仿真得到的共模电感周围的磁场强度的幅值如图3所示。

图1 共模电感实物图

图2 共模电感三维仿真模型图

图4是共模电感与其他磁性元件的磁路等效图，其中Rcm1和Rcm2为共模电感磁环中左右两部分的等效磁阻，Rg1、Rg2为空气回路的等效磁阻，R为其他磁性元件的等效磁阻。由于共模电感通入等大同相的共模电流激励，根据叠加定理可得，这两个共模电流激励产生的磁势对其他磁性元件产生的磁通等大反相，刚好抵消，因此共模电感共模分量产生的磁场基本不影响其周围的磁性元件。

图3 共模电感周围磁场强度分布图

图4 共模电感对外磁路等效图

2.2 共模电感器差模电感分量磁场分布

图5和图2的模型是一样，只是所赋电流激励的方向不一样，图5中共模电感中通入方向相反的电流激励来仿真其在差模电流下的磁场分布。仿真得到的共模电感周围的差模磁场的分布如图6所示。

共模电感的差模磁路等效图如图7所示，其中Rdm1和Rdm2为共模电感磁环中左右两部分的等效磁阻，Rg为磁环中间的空气等效磁阻，Rg1、Rg2为磁环外从磁环到其他磁性元件的空气回路等效磁阻，R为其它磁性元件的等效磁阻。共模电感通入等大反相的差模电流激励，根据叠加定理可得，共模电感两个差模电流激励产生的磁势对其他磁性元件产生的磁通等大同向，是叠加的关系，因此共模电感差模分量产生的磁场会影响其周围的磁性元件。

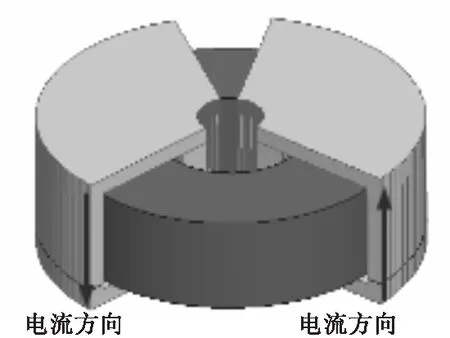
图5 共模电感差模分量三维仿真模型图

图6 共模电感周围磁场强度分布图

图7 磁路等效电路

2.3 变压器外部磁场分布

图8为PCB变压器的三维仿真模型图，其基本结构为原边5匝，副边3匝，原边为铜箔绕制而成，副边为PCB绕组。其实际工作时的电流方向如图8(a)中红色直线所示。

变压器外部磁场的分布图如图9所示，可以看到变压器对外还是存在一定的磁场泄漏，这个泄漏的磁场会影响到其周围的磁性元件。

变压器往外泄漏的磁场是由于变压器原边和副边绕组在窗口外面等效的一匝线圈引起的，如图8(b)所示。该变压器对外等效的磁路图如图10所示，其中Rg1、Rg2为原边绕组等效一匝漏磁从变压器原边窗口到其他磁性元件的空气回路等效磁阻，Rg3、Rg4为副边绕组等效一匝漏磁从变压器副边窗口到其他磁性元件的空气回路等效磁阻，R为其他磁性元件的等效磁阻。可以看到变压器原边和副边绕组对外产生磁势的方向是叠加的，因此变压器工作时，会影响到周围其他磁性元件。

图8 变压器三维仿真模型图

图9 变压器周围磁场强度分布图

图10 变压器外部的磁路等效图

3 磁性元件的近场耦合解耦

3.1 近场耦合的原理

磁场耦合模型可以通过互感M来表示，因而在EMI滤波器的电感与电容的近场耦合模型中表现为一个受控电压源的形式，如图11所示，图中电流I为流过干扰源的电流。

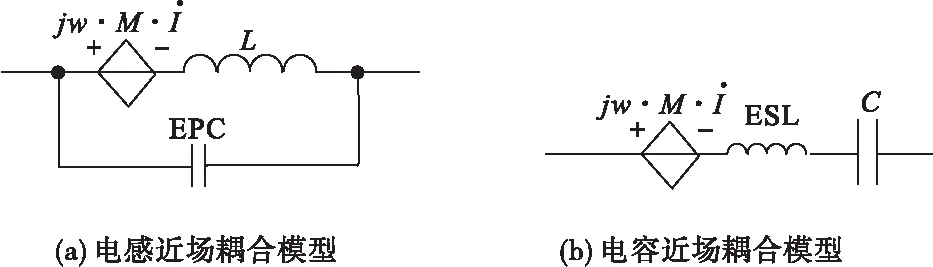
图11 电感与电容近场耦合模型

3.2 近场耦合解耦原理

由于EMI滤波器有多个磁性元件与电容元件，它们间的耦合关系也更为复杂，不利于对其相互影响的分析。可以根据电路原理，先将存在耦合关系的元器件进行解耦，再分析其近场耦合效应，如图12～16所示为基本电路原理的解耦方法。

图12 电感正耦合解耦示意图

图13 电感负耦合解耦示意图

图中两个电感L1与L2存在互感M，分别为正耦合和负耦合。通过公式可以实现电路的解耦。

(1)

(2)

3.3 共模电感与X电容的T型近场耦合解耦

由于EMI滤波器往往是带有两个共模电感与X电容的T型结构，如图14所示。其中，M1为L1与L3间的互感，M2为L1与L4间的互感，M3为L2与L3间的互感，M4为L2与L4间的互感，M5为L1与X电容ESL间的互感，M6为L3与X电容ESL间的互感，M7为L4与X电容ESL间的互感，M8为L2与X电容ESL间的互感。假设共模电感与X电容寄生电感ESL为正向耦合。

同样利用电路解耦方法，可以将图14所示电路解耦为图15所示。

由于L1与L4、L2与L3没有共同的节点，不能通过简单的电路解耦方法进行解耦。先将电路中已解耦的参数忽略，得到图16，其中，i1、i2、i3、i4为共模电感四个绕组上的电流。

图14 T型滤波器近场耦合示意图

图15 T型滤波器近场耦合部分解耦示意图

图16 共模电感绕组无共同节点的近场耦合模型

根据互感原理可得公式:

(3)

假设

(4)

将互感的影响通过受控源表示，则图16可以变为图17所示。

图17 共模电感绕组无共同节点的近场耦合简化模型

由于EMI滤波器的对称性，认为i1=i2，i3=i4，M2=M3，将公式化简为：

(5)

从公式(5)即可实现图17的解耦，如图18所示。

图18 共模电感绕组无共同节点的近场耦合解耦模型

通过上述方法，即可实现Τ型电路的完全解耦，如图19所示。同时，可以得到每条支路的近场耦合电感值。

4 磁性元件间近场耦合的仿真及测试方法

磁性元件间的近场耦合测量方法有三种：(1)互感测量法；(2)网络分析仪法；(3)仿真法。

图19 T型滤波器近场耦合完全解耦模型

4.1 仿真法提取共模电感间近场耦合参数

HFSS是一个功能强大的电磁场仿真软件，广泛应用于各种工程电磁场领域。它基于麦克斯韦微分方程，采用有限元离散的方式，将工程电磁场的计算转变为矩阵求解，其具有易于操作与仿真准确等特点，这里使用HFSS的三维模型来进行两共模电感近场耦合的仿真。

如图20所示为实验样机的EMI滤波器结构图。根据EMI滤波器的放置方式，在HFSS软件中建立其三维模型，如图21所示。由于共模电感绕组较多，且绕制并不均匀。为了便于建模并准确的模拟实际电感，共模电感模型的绕组采用单匝绕制，在计算互感时，将得到的结果再乘以匝数。

图20 实验滤波器放置示意图

图21 三维模型

仿真EMI滤波器的磁耦合参数必须为共模电感模型赋激励电流源，在HFSS仿真模型中设置对应的电流方向，如图22红色箭头所示。

图22 共模电感模型电流方向

图23 HFSS仿真的存在耦合的两器件原理图

由于用HFSS软件仿真得到的结果是S、Y、Z参数，这里可以根据仿真得到的Z参数来计算得到两器件间的互感，这是因为如图23所示，对于两个存在近场耦合的器件，可以把它们看做是一个二端口网络，这个二端口网络满足公式(8)、(9)，其中:

(6)

(7)

(8)

因此，

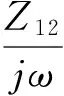
(9)

将仿真得到的共模电感CM1与CM2之间的Z参数，如图24所示，带入公式(9)中得到两共模电感间的近场耦合参数，如表1所示。

根据表1的仿真结果可以看到，M1、M2、M3、M4的数值基本差不多，按照3.3小节的T型滤波器近场耦合的解耦模型，由于解耦后，两共模电感中间的X电容的寄生电感为0.263μH，导致两共模电感中间X电容的谐振频率变小，降低EMI滤波器对差模的抑制能力，同时影响共模电感差模分量的互感参数与差模分量相比较小，可以忽略不计。

图24 EMI滤波器近场耦合仿真结果

M165.57M265.75M365.44M465.99

4.2 互感测量法

若两磁性元件距离较近，耦合系数较大，可以用互感测量法来测得两者间的耦合系数。如图25所示，通过将干扰体与被干扰体按如图26(b)、(c)的方式进行串接，即正、反串，并分别测量两种情况的电感。再通过一定的计算得到耦合电感M。

图25 互感测量法

“正串”时，如图25(b)：

Ltest1=L1+L2+2M

(10)

“反串”时，如图25(c)：

Ltest2=L1+L2-2M

(11)

则干扰体与被干扰体的互感为：

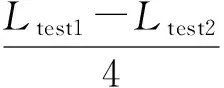
(12)

如图26所示，样机中两共模电感距离很近，因此可以采用互感测量法来得到两共模电感间的近场耦合参数M。通过仿真可知M13、M23、M14、M24的数值很接近，因此假设M13=M23=M14=M24=M。根据上面两电感间互感的推导方法可将图26的电路图解耦为图27所示的电路图，因此：

图26 互感测量法测量两共模电感间的互感测试图

图27 互感测量法测量两共模电感间的互感的解耦电路图

Ldm1=2LCM1-2M1

(13)

Ldm2=2LCM2-2M2

(14)

Ltest=2LCM1-2M1+2LCM2-2M2+8M

(15)

(16)

通过阻抗分析仪测得Ldm1为2.034μH，Ldm3为1.995μH，Ltest=4.571μH，根据公式(16)可得，M为0.068μH，而通过仿真法得到的两共模电感间的互感M的平均值为0.0657μH，两者误差约为3.4%。因此，通过HFSS软件仿真得到的共模电感间的近场耦合参数是可行的。

5 结论

本文首先分析了共模电感与变压器在工作时的磁场泄露情况及对其他磁性元件的影响，通过分析可以看到，在实际工作时，共模电感的差模分量的磁场对外界有着较大的磁场干扰，而共模分量的磁场对外界影响则较小；变压器原副边对外界均有着一匝回路，这一匝回路同样对外界其它磁性元件会产生干扰。其次，分析了磁性元件间近场磁耦合机理并通过电路解耦原理对共模电感器与X电容的T型近场耦合进行解耦，其解耦后会在X电容上产生一个互感与X电容本身的ESL进行叠加，叠加后会使得滤波器的高频滤波性能变差。最后通过三维电磁场仿真软件HFSS仿真得到共模电感间的磁耦合参数，并用实验验证仿真得精度。

[1] 李龙涛.开关电源传导 EMI 建模和模型有效性评估[D].哈尔滨工业大学,2012.

[2] 王拓.开关电源传导EMI仿真分析[J].通信电源技术,2008,25(5):15-18.

[3] 张煜,陈庆彬,陈为,等.开关电源传导电磁干扰仿真研究[C]//中国电源学会第二十届学术年会论文集,2013:1205-1209.

[4] 孟进,马伟明,张磊,等.开关电源变换器传导干扰分析及建模方法[J].中国电机工程学报,2005,25(5):49-54.

[5] 马垠飞.开关电源传导EMI的预测研究[D].河北:河北工业大学,2012.

[6] 陈庆彬,陈为.开关电源中变压器共模传导噪声抑制能力的评估方法[J].中国电机工程学报,2012(18):73-79.

[7] 陈庆彬.开关电源磁性元件传导EMI特性及滤波器近场耦合特性研究与应用[D].福州：福州大学，2012.

[8] 许珂.电力电子装置共模电磁干扰分析及抑制技术研究[D].重庆:重庆大学,2012.

ArtificialAnalysisofNearFieldMagneticCouplingoftheMagneticElements

HUQin-jun,CHENWan-chun,HUANGJing

(Zhangzhou Power Supply Company,Zhangzhou 363000,China)

Magnetic elements such as,inductance,common-mode inductcence,transformer and so on are important parts of power transformers.Their setting places and wiring ways can affect the inhibitory action on electromagnetic interferference noise.As power inverter is more and more miniaturization and high power density,their elements are compactly placed.The near field coupling effect exists among vaouris elements.The paper analyzes the near field magnetic coupling mechanism between magnetic elements and verified correctness of the near field mugnetic coupling parameters between the magnetic elements by experiment.

magnetic element;magnetic coupling;parameter correctness

1004-289X(2017)03-0035-07

TN624

B

2016-12-27