DLS-Ⅱ型负压计在测定土壤水势中的应用研究

，， ，

(河北省环境地质勘查院，河北 石家庄 050021)

DLS-Ⅱ型负压计在测定土壤水势中的应用研究

张志飞，胡现振，郭强，张辉军

(河北省环境地质勘查院，河北 石家庄 050021)

负压计是测定土壤水基质势的仪器，安装及操作简便。DIS-Ⅱ型负压计作为负压计的一种，具有其独特的优点，现已在作物生长、陆地水文循环、土壤水分运移等研究领域得到了广泛应用。本文通过对DLS-Ⅱ型负压计的结构及原理的研究，进一步推求负压计的起算零点和量程，并给出验证负压计可靠性的方法。对试验过程中浅层负压计水银柱随气温升高而下降及注水时拔出铝铆钉集气瓶冒水问题进行了探讨。通过对试验数据的分析，结果表明DLS-Ⅱ型负压计应用效果比较理想。

DLS-Ⅱ型负压计；土壤水势；起算零点；量程；可靠性；应用效果

负压计(又称张力计)是测定土壤水基质势的仪器，也是土壤水研究中唯一能观测能量的一种仪器[1]。由于其结构简单，易于制造、安装及操作简便，适宜在田间使用，目前，负压计已成为测定土壤水基质势的常规仪器[2]。国内外常用的负压计有不同种类，从压力传导方式上可分为水传与气传两种，在压力测定上有表头式、水银式、水柱式、压力传感器式等等，每一种负压计又可分为若干种[1,3,4]。DLS-Ⅱ型负压计是负压计的一种类型，属水银式负压计,由中国科学院地理科学与资源研究所于2006年研制[5]。DLS-Ⅱ型负压计除具有负压计的一般特点外，还具有其独特的优点，现已广泛应用于作物生长、陆地水文循环、土壤水分运移等研究领域[6,7,8]。

然而，目前尚未见关于DLS-Ⅱ型负压计的深入研究成果。试验过程中，DLS-Ⅱ型负压计是否处于正常状态，影响着测定结果的准确性，甚至决定着试验的成败。所以，清晰了解负压计的结构、原理、特征及在使用过程中可能遇到的问题，及时判断和掌握仪器的运行状况，确保负压计始终正常运行，对试验来说至关重要。

1 DLS-Ⅱ型负压计结构及原理

1.1 结构及原理

DLS-Ⅱ型负压计主要由多孔陶土管，集气室和水银压力计联接而成[5](图1)。多孔陶土管是仪器的感应部件，它是由具有均匀微细孔隙的陶土材料制成的。当陶土管充满水后，管壁便形成张力相当大的水膜，在一定的压差范围内，水分和溶质可以通过管壁，而气体则不能通过，即所谓透水不透气[4,9]。把陶土管埋入土壤后，其内的自由水便通过陶土管的孔隙与土壤水连接，产生水力上的联系。当陶土管内的水势与土壤水的水势不相等时，水便由水势高处向水势低处流动，直至两个系统的水势平衡为止。平衡后水银压力计显示的读数值，经过换算就可得到当时陶土管所在位置土壤水的基质势。

与陶土管相连接的是加水管和导压软管，加水管深入到陶土管内腔的最底部，导压软管处于内腔顶部，这样在注水排气时便很容易将陶土管内的气体排出。导压软管的另一端连接集气瓶底部的一个接口。集气瓶安装在负压计的最高位置，可使陶土管与导压管内产生的气体自动升至集气瓶内，即通过导压软管实现陶土管向集气瓶的负压传递。集气瓶底部的另一个接口与水银测压管相连，水银测压管底端位于水银槽的水银内。集气瓶内的负压将会引起水银柱的上升。在注水完成后，用铝铆钉和橡皮塞分别将加水管口和集气瓶口进行封堵，整个负压计便成为一个封闭系统，陶土管产生的负压值将会完全反映在水银柱的高度上，由水银柱高度值便可求出陶土管所处位置的土壤水基质势1。

水银柱高度表示的是由负压计系统本身高差引起的高度和土壤基质吸力引起高度的和值，土壤水基质势需要通过计算才能得到，计算公式为：

φ=12.6(h+Δh)-H(cmH2O)

换算成压力标准计量：

φ=[12.6(h+Δh)-H]/10.2(kPa)

其中，Φ为土壤基质势，即负压值(kPa)；h为水银柱上升的高度(cm)；H为陶土管中间与水银槽中水银面之间的距离；△h为水银柱上升后，水银槽中的水银面下降的高度(cm)；当水银的面积较大时△h很小，可取△h=0。

1.2 DLS-Ⅱ型负压计的特点

DLS-Ⅱ型负压计具有以下特点：陶土管埋设时不破坏土壤结构；测量采用水银压力计，具有较高精度；设有加水管和集气瓶，容易除气，可一次更换陶土管里的水；导压管采用软管，软管埋设可远离测点进行观测，避免了水沿硬管壁快速入渗和人为破坏测点环境的影响；陶土管长期埋在土壤里内壁如有污垢，不需要挖出即可清洗；测试过程不受任何土质影响，只要水势一样，作物生长状态就一样；整个土壤剖面上负压计的读数在同一观测板上实现,可以很清楚的看到整个土壤剖面基质势的变化趋势；制作简单，操作也简单，价格便宜，测读方便，可定点定位连续测定。

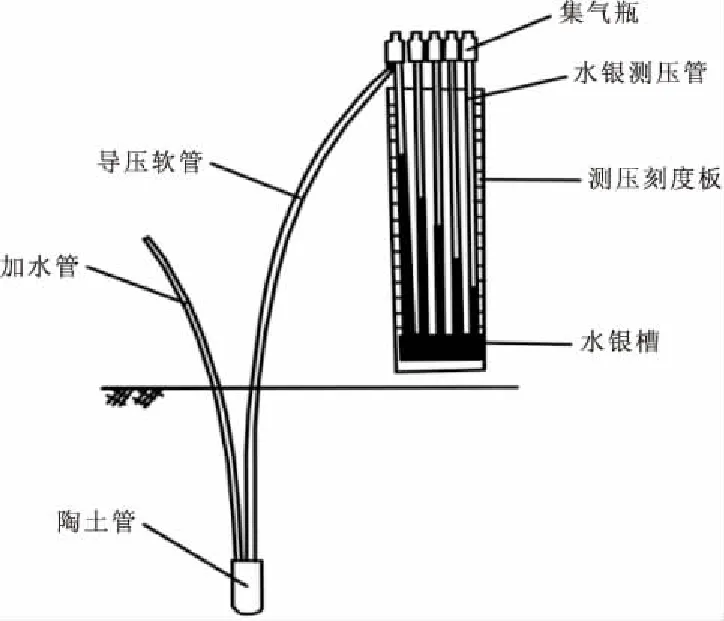
图1 DLS-Ⅱ型负压计结构图

2 起算零点的计算确定

DLS-Ⅱ型负压计的观测板安装在地面以上，多孔陶土管埋设在地面以下。由于水银槽中水银液面与陶土管之间存在高度差，即使在土壤水基质势为零时，在压力差的作用下水银测压管中水银柱亦会上升一定的高度，此高度值所在的位置即为起算零点。当水银柱高度低于起算零点时，说明负压计系统尚未达到稳定状态；当水银柱高度高于起算零点时，超出起算零点的部分则是由土壤基质吸力引起的，此值表征了土壤基质势的大小。起算零点的计算有两种方法：负压力平衡法和压强平衡法。

2.1 负压力平衡法

负压力平衡计算公式为：

ρw(H+h)=ρH(a+Δa)

(1)

式中：H为土壤水分压力(cm)；h(=a+△a+b)为多孔陶土管的中部到水银柱的高度(cm),其中，a为从零点到水银柱的高度(cm)，△a为由于水银上升造成水银槽中水银下降的部分(cm)，b为从零点到多孔陶土管的中部的高度(cm)；ρω为水的比重(1)；ρH为水银的比重(13.6)，各值如图2所示。

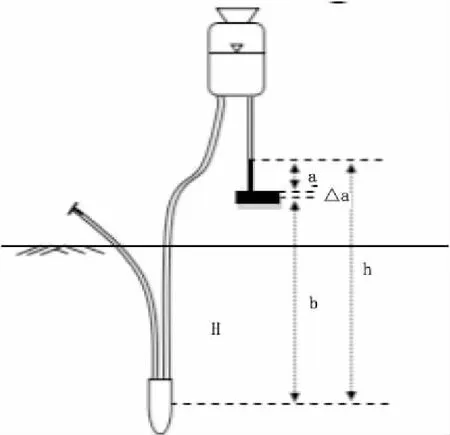
图2 负压力平衡法计算示意图

因为水银槽直径比管径大得多，可设△a=0，则h=a+b，式(1)可写成

ρw(H+a+b)=ρHa

(2)

取ρω=1，ρH=13.6则

H=(ρH-ρw)a-b=(13.6-1)a-b

(3)

所以

H=12.6a+b

(4)

取土壤水分压力为零(H=0)，则可求得起算零点值。从(4)可知：

a0=b/12.6

(5)

2.2 压强平衡法

利用压强平衡计算起算零点时，假定多孔陶土管处土壤基质势为零，即不受到土壤基质势的作用，仅考虑由负压计系统本身的压强差所引起的水银柱高度。在有些地区，地下水位埋深较浅，在试验期间，多孔陶土管很可能会处于地下水位以下，因此，分为地下水位处于陶土管以下和地下水位处于陶土管以上两种情况分别进行计算。

1)地下水位处于陶土管以下图3 (a)

多孔陶土管一侧由压强平衡得：

P′+ρwg(a+h+H)=P0

(6)

水银槽一侧由压强平衡得：

P′+ρwga+ρHgh=P0

(7)

联立式(6)、(7)，并化简得起算零点计算公式：

h=H/12.6

(8)

式中：P＇为集气瓶中空气压强；P0为大气压强；ρω为水的密度；ρH为水银密度；g为重力加速度；a为水银柱顶端至集气瓶中水面的高度；h为水银柱上升高度；H为多孔陶土管中间至水银槽中水银面的高度。

2)地下水位处于陶土管以上图3 (b)

由示意图可知，当陶土管位于地下水位以下时，陶土管一侧的压强平衡式为:

P′+ρwg(a+h+H)=P0+ρwgx

(9)

水银槽一侧由压强平衡得：

P′+ρwga+ρHgh=P0

(10)

联立式(9)、(10)，并化简得起算零点计算公式：

h=(H-x)/12.6

(11)

式中：x为地下水面至多孔陶土管中间的距离，其余符号的含义同1)。

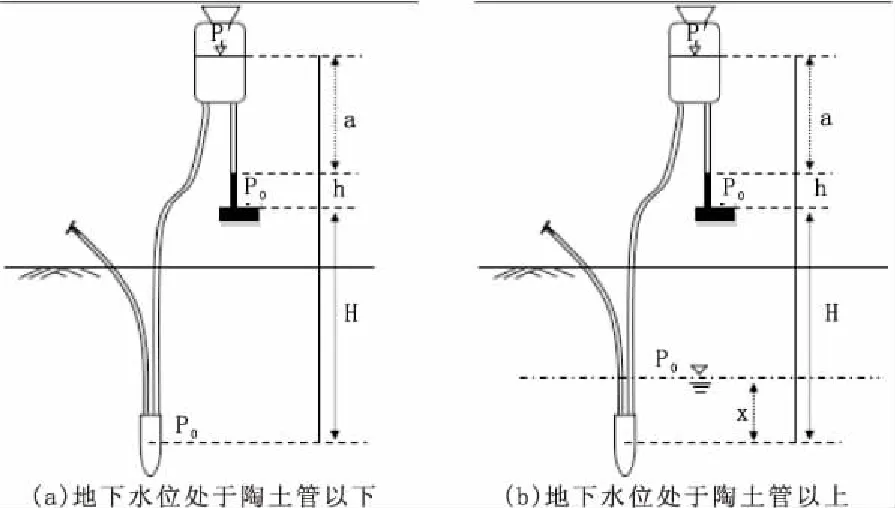
图3 压强平衡法计算示意图

3 负压计量程

DLS-Ⅱ型负压计的量测系统为直管水银压力计[5],土壤基质势的大小通过水银柱上升高度显示。而水银柱能够上升的最大高度由当地的大气压决定，不同地区、不同海拔高度、不同温度条件下的大气压强大小不一，所以不同地区的负压计量程有所不同。大气压强大越大，所支持的水银柱上升高度越高，则负压计的量程越大。反之，量程越小。此外，直管水银压力计的量程还受陶土管埋置深度的影响。由于水银槽中水银面与陶土管之间存在一定的高差，此高度差亦会引起水银柱的上升一定高度，即负压计起算零点。起算零点越高，则负压计能够量测的范围越小。因此起算零点以上至当地大气压能够支持的水银柱高度区间即为负压计的量程。

R=H0-a0

式中：R为负压计量程(cm)；H0为当地大气压所能支持的水银柱高度(cm)；a0为起算零点(cm)。标准大气压为值为101.325 kPa，由DLS-Ⅱ型负压计所量测土壤基质势的绝对值最大值一般均小于此值。

图4 埋深160cm负压计起算零点理论值与观测值对比图

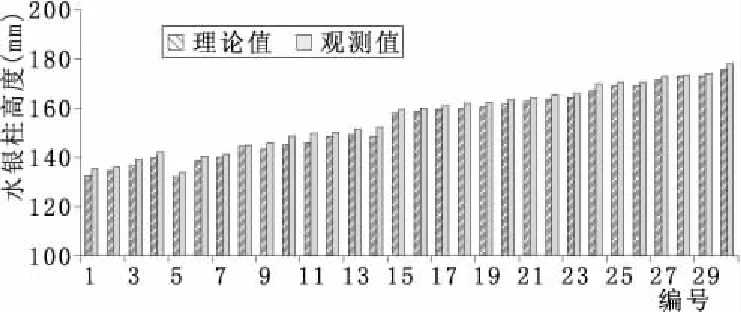
图5 埋深180 cm负压计起算零点理论值与观测值对比图

4 负压计可靠性验证

负压计的关键部件是多孔陶土管，它的性能和质量决定着由负压计测定的土壤水势的准确性，进而影响着研究成果的水平。因此，在试验时很有必要对所使用的负压计的可靠性进行验证，以确保所测结果准确无误。上面已经讨论了起算零点的确定，那么就可以通过起算零点观测值与理论值的比较，验证负压计的可靠性。多孔陶土管在非饱和土壤和空气中均会受到表面张力作用而使得测量值高于起算零点，利用起算零点进行验证需要消除这种作用，使水银柱理论观测值等于起算零点。由于饱和土壤的基质势为零，因此可以在土壤处于饱和状态时对负压计进行验证(在安装前进行验证时，则可以将陶土管浸没在水中)。

笔者在野外试验过程中，有一段时间为农灌期，地下水位埋深较浅，埋设于160 cm、180 cm、200 cm深度的陶土管处于地下水位以下，则观测值应等于起算零点。因此，我们利用这一时间段不同水位埋深所对应的观测值对三种深度陶土管的可靠性进行了验证。

以上利用随机选择的30组不同地下水位埋深和所对应的水银测压管观测值，并通过公式(11)计算出起算零点理论值，分别对埋深160 cm、180 cm、200 cm的负压计进行了验证。从三支负压计理论值和观测值对比来看，其差值在1～4 mm之间，且观测值均高于理论值。分析可知，此误差为外部因素引起的系统误差，原因是所测的地下水位埋深值和陶土管埋深值均存有一定的误差。所以，在此微小误差范围内，完全可以认为试验所使用的负压计是可靠的。

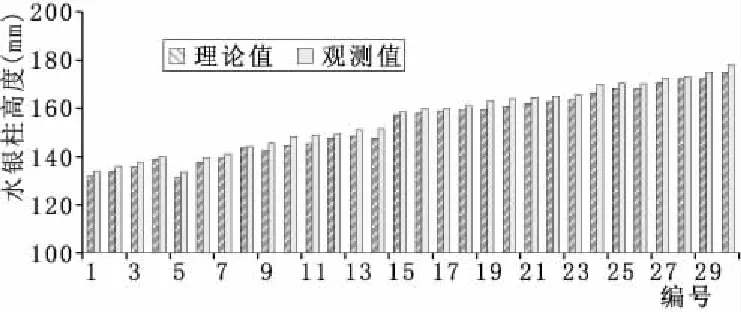
图6 埋深200 cm负压计起算零点理论值与观测值对比图

5 试验过程中的问题探究

5.1 温度较高时，水银柱下降现象

由于试验需要我们对负压计进行了加密观测,每2个小时观测一次。在观测过程中发现，在上午10点以后，随着气温逐渐升高，埋设深度为10 cm、20 cm、30 cm负压计的水银柱出现了下降现象，直至下午3-4点水银柱才开始回升，观测数据见表1。

此种现象引起了我们的关注和思考，直观判断，随着气温的升高，土壤水分不断蒸发，含水率降低，土壤水基质势增大，负压计水银柱应该上升。但实际并非如此。原因在于土壤不同深度处温度不同，在温度场的温度梯度作用下，包气带中的气态水会通过孔隙向温度低的方向运移，使温度较低区域的土壤含水量增加[10]，基质势减小，进而使得负压计水银柱高度下降。在大气温度较高时，一般在地表以下5～40 cm深度范围内为温度低值区[11]，其上下部分土壤温度均高于此区域，在温度梯度的作用下，气态水分会在此聚集、凝结，因此，埋设深度为10 cm、20 cm、30 cm负压计的水银柱出现了下降现象。

5.2 注水排气时，拔出铝铆钉集气瓶冒水现象

DLS-Ⅱ型负压计用水作为压力传导介质，由于陶土管中的水势一般会高于土壤水势，水就会由水势高处向水势低处流动，陶土管中的水便不断流进土壤，直到两个系统的水势达到平衡为止。因此，需要定期为负压计注水排气。在注水时有个很明显的现象，当拔出封堵加水管的铝铆钉的同时，会有相当数量的水从导压软管中冒出，进入到集气瓶中，而且，土壤越干、水银柱上升越高冒出水量越大。

对此现象，笔者做了初步的分析研究。负压计是一个气体封闭系统，陶土管也只透水不透气。当陶土管中的水不断进入土壤后，负压计系统内将形成一定的负压，此负压将反应到集气瓶中。在土壤干燥情况下，负压计中水量消耗较多，集气瓶中会形成较大的负压值，当拔出铝铆钉后，封闭系统便与大气连通，在较大气压差作用下，加水管、陶土管和倒压软管中的水将被压入集气瓶，从而产生集气瓶冒水现象。详细的论证,尚需进一步的试验研究。

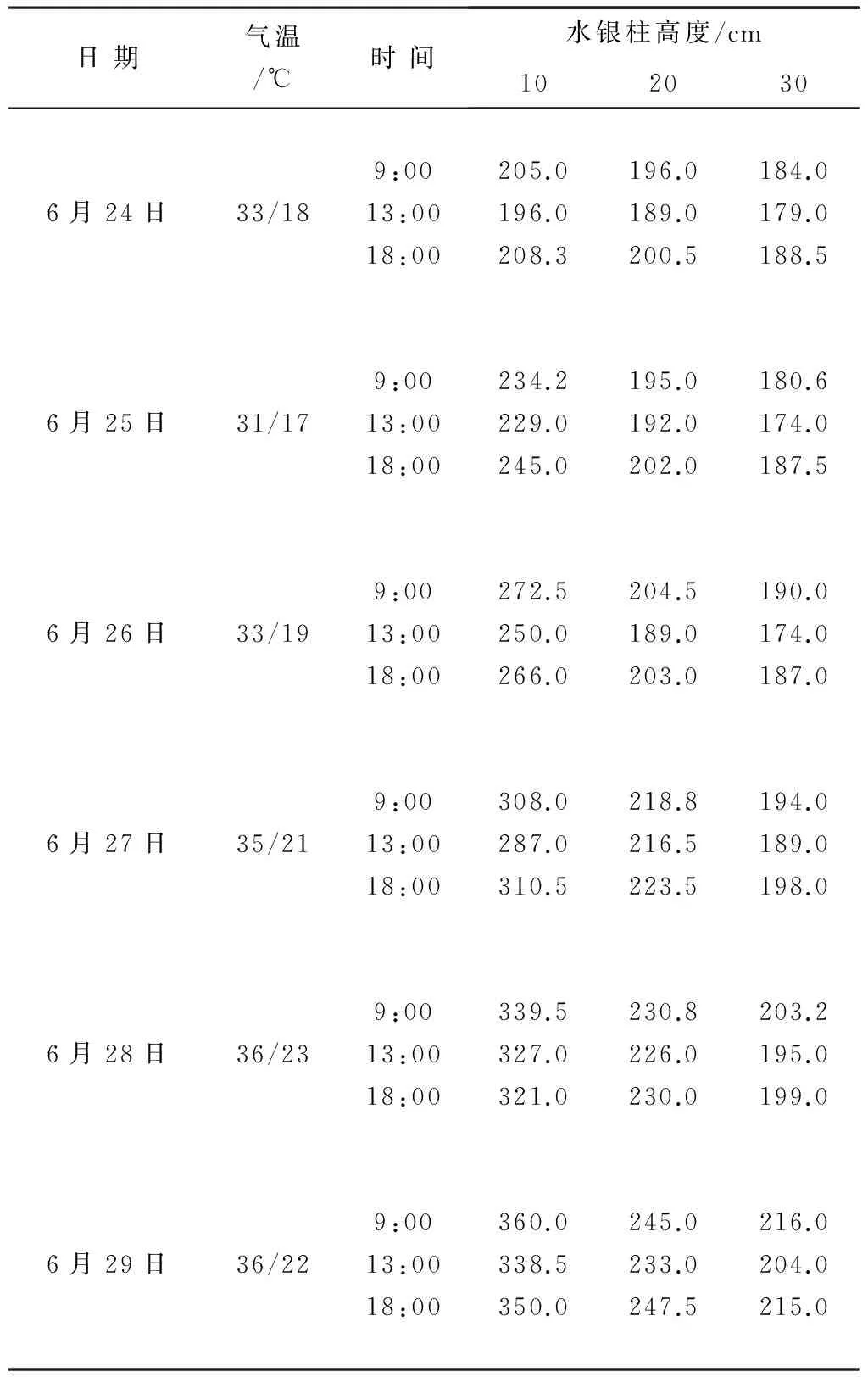
表1 埋深10 cm、20 cm、30 cm负压计

6 应用效果

应用DLS-Ⅱ型负压计在宁夏中宁县试验点进行了原位试验，取得了较好的效果。试验点陶土管的埋设深度为10 cm、20 cm、30 cm、40 cm、50 cm、60 cm、70 cm、80 cm、90 cm、100 cm、120 cm、140 cm、160 cm、180 cm、200 cm。试验期间，根据灌溉和天气变化情况及试验需要，每天进行了不同频次的观测，并将每次观测的数据进行了整理计算，绘制出了土壤剖面水势分布曲线，这些曲线均较好的反映出了土壤剖面水势变化情况。

试验期间6月19日-21日试验点出现了一个间断降雨过程，图7便是由DLS-Ⅱ型负压计所测得的此降雨过程的土壤剖面水势分布曲线。从图上可以清晰的看到本次降雨过程土壤剖面水势的变化。在降雨前，土壤剖面处于蒸发状态，在降雨之初，地表土壤逐渐湿润，土壤水势增加，表层土壤水势曲线逐渐右移(如曲线19..08、19..20、20..08)。在湿润锋以上，土壤水势梯度∂ψ/∂z>0,土壤水分不断下渗，而在湿润锋以下，土壤水势梯度∂ψ/∂z<0，土壤水分仍然向上运移，所以在湿润锋处形成一个收敛型零通量面(ZFP(C))[3](如曲线20..14)。随着降雨的进行,土壤表层水势不断增大，湿润锋逐渐下移，ZFP(C)也逐渐向下发育。此过程曲线有力的证明了正确使用DLS-Ⅱ型负压计所取得的效果。

图7 试验点6月19日—21日土壤剖面水势分布曲线

7 结语

负压计是测定土壤水基质势的重要仪器，在土壤水分运动的研究中得到了广泛的应用。在试验过程中如果对负压计的结构和原理能够很好的了解和掌握，对遇到的一些问题和现象有充分的认识，那么负压计使用将会得心应手。对负压计系统的透彻理解和熟练运用不仅可以保障试验的顺利进行，而且可以取得较好的试验效果。

[1]刘昌明.水文水资源研究理论与实践.刘昌明文选.北京市：科学出版社.2004.222-225.

[2]刘荣豪,裴亮.土壤水基质势研究进展[J]. 节水灌溉.2012.(6):34-36.

[3]荆恩春,费瑾,张孝和,等.土壤水分通量法实验研究[M].北京:地震出版社.1994.

[4]荆恩春，张孝和，等.WM-1型负压计(系统).水文地质工程地质研究所所刊.1990(6).

[5]中国科学院地理科学与资源研究所.一种土壤水分张力计:中国专利.CN200520110647.6[P].2006-08-23.

[6]窦超银,康跃虎,万书勤.地下水浅埋区重度盐碱地覆膜咸水滴灌水盐动态试验研究[J]. 土壤学报.2011.48(3):524-532.

[7]姚素梅,康跃虎,刘海军.喷灌与地面灌溉冬小麦根系生长和分布的比较研究[J].水资源与水工程学报.2010.21(4): 1-5.

[8]穆文彬.华北平原农田层状土壤水分运动试验及数值模拟[D].华北水利水电学院.2012.

[9]中国科学院南京土壤研究所水分组.土壤湿度计的原理与应用[J]. 土壤.1976.(4):228-233.

[10]万力,曹文炳,周训,等.包气带中温度变化对水分分布影响的实验研究[J]. 水文地质工程地质.2004.(03):25-28.

[11]戴长雷,邓柏旺,李治军.包气带垂向含水率日变化特征试验研究[J]. 黑龙江水专学报.2009.36(2):16-20.

[12]方正三,蔡文寬,王庚雄.负压计(土壤湿度计)的原理、构造设计及其应用[J]. 土壤通报.1964.(03):33-40.

[13]Richards,L.A.,Methods of Measuring Soil Moisture Tension,Soil Science，1949.68(01):95-112.

ApplicationofDLS-IInegativepressuremeterindeterminationofsoilwaterpotential

ZHANGZhi-fei，HUXian-zhen，GUOQiang，ZHANGHui-jun

(Hebei Environmental Geology Exploration Institute, Hebei,Shijiazhuang 050021, China)

Negative pressure meter is an instrument for determining soil water potential, and it is easy to install and operate. As one of the negative pressure meters, DIS- II negative pressure meter has its unique advantages. It has been widely used in the fields of crop growth, land hydrological cycle, soil water transport and other fields. In this paper, the structure and principle of DLS- II negative pressure meter are studied. The starting zero and range of the negative pressure meter are further deduced, and the method to verify the reliability of the negative pressure meter is given. In the test process, the shallow negative pressure gauge mercury column drops with the increase of temperature and the problem of water pumping out of the aluminum rivet collection cylinder during water injection is discussed. Through the analysis of the experimental data, the results show that the application of DLS- II negative pressure meter is ideal.

DLS- II negative pressure meter；soil water potential；zero starting point；range；reliability；application effect

S152.7+1

A

1004-1184(2017)05-0167-04

2017-04-26

张志飞(1982-)，男，河北邢台人，工程师，主要从事水文地质、工程地质及环境地质方面工作。