水库下游悬移质泥沙沿程恢复研究进展

，，，

(1.长江科学院 水利部江湖治理与防洪重点实验室，武汉 430010;2.湖南省水利水电勘测设计研究总院，长沙 410007)

水库下游悬移质泥沙沿程恢复研究进展

贺方舟1,2，朱勇辉1，郭小虎1，陈栋1

(1.长江科学院 水利部江湖治理与防洪重点实验室，武汉 430010;2.湖南省水利水电勘测设计研究总院，长沙 410007)

2017,34(12):1-6

水库下游悬移质泥沙沿程恢复是河流泥沙动力学研究的难点问题之一。对该问题的研究有助于推动学科发展，解决工程实践中的有关问题。针对此现状，归纳总结了平衡及不平衡输沙条件下悬移质浓度垂线分布、悬移质沿程恢复的天然河道实测资料分析和恢复饱和系数等方面的研究成果，认为在不平衡输沙条件下悬移质泥沙垂线分布研究及实测数据的获取、分析等方面还存在一定的不足。在此基础上，提出有必要进一步开展水库下游悬移质泥沙沿程恢复研究，特别是利用精准的测量仪器，开展科学合理、系统全面的水槽试验是丰富该研究成果的必要手段。

悬移质泥沙；不平衡输沙；悬移质浓度垂线分布；恢复饱和系数；研究进展

1 研究背景

自然河流发育演变过程中，悬移质泥沙起着极为重要的作用。冲积平原河流中悬移质的数量往往是推移质的数百倍，山区河流中前者也是后者的数10倍[1]。近年来，我国在大江大河上修建了众多水利工程。水库向下游输水输沙过程中，存在水体含沙量由非平衡向平衡状态转变并伴随着水体挟带泥沙做功、克服各类阻力做功等能量重新分配和转化过程。在实际中，水库的运用使得坝下游下泄的水流含沙量明显减少，水体泥沙组成变细。官厅水库蓄水后，3 a内永定河下游含沙量减少到蓄水前的1/10[2]。丹江口水库建成后也存在同样的情况[3]。水流含沙量降低导致水流挟沙能力处于次饱和状态，悬移质含沙量将会沿程恢复，带走河道中的泥沙，从而导致水库下游河道长距离冲刷，使得河势剧烈调整，可能对下游的防洪、航运、水资源利用、水生态环境等带来一系列不利影响。

研究不平衡输沙条件下的悬移质浓度垂线分布和沿程变化规律有助于进一步了解河流泥沙输移规律，而基于二维恒定流条件下的水槽试验能对已有公式进行检验，或改进相关系数，使相关条件下系数选取更加细化，从而提高模拟精度，仍有实际意义。

2 悬移质含沙量垂线分布理论

20世纪以来，国内外众多学者在对悬移质含沙量垂线分布的研究中取得了一系列成果，现简述如下。

2.1 平衡输沙条件下悬移质含沙量垂线分布研究

奥布莱恩-劳斯[4]于20世纪30年代首先基于扩散方程，对水流条件采用了二维恒定均匀流假定后，提出了Rouse公式,即

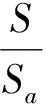
(1)

式中:S为距床面y处的悬沙浓度；Sa为y=a点处悬沙浓度；h为水深；ω为泥沙沉速；κ为卡曼常数；U*为床底摩阻流速。

Rouse公式在实际应用中精度尚可，使用较广泛。但公式存在计算后水面含沙量为0及床面含沙量为无穷大2个问题。针对这些不足，学者们对Rouse公式推导过程中的相关参数进行了改进。

张瑞瑾[1]、陈永宽[5]、冷魁等[6]、张红武等[7]、Lane等[8]、Chiu等[9]对流速公式进行了改进，建立了不同形式的含沙量垂线分布计算式。

Vanoni[10]、Van Rijn[11]对泥沙扩散系数εs进行了改进，探究了扩散系数εs与动量交换系数εm的比例关系。王兆印等[12]根据管道悬移质试验资料，认为β=εs/εm=1.3。倪晋仁等[13]探讨了影响泥沙扩散系数εs的因素，认为泥沙的物理属性对εs都有明显影响，传统理论描述泥沙颗粒垂线分布时仍有不足，动理学将在描述悬浮泥沙运动中具有应用前景。

倪晋仁等[14]考虑Richardson等[15]的群体沉速公式，张小峰等[16]考虑黏性流体的非滑移条件，通过改进泥沙颗粒沉速，分别得到新的悬移质含沙量沿垂线分布的计算式。

学者们也从修正悬浮指标Z的角度对含沙量垂线分布公式进行了研究。Einstein等[17]提出“扩散理论的第二近似解”，导出了测量悬浮指标Z测与计算悬浮指标Z计的理论关系。此后Monts等[18]、谢鉴衡等[19]也做过相应研究，从结果来看Z测与Z计之间的关系仍有待明确。

倪晋仁等[20]在研究固液两相流运动中关于悬移质含沙量分布问题时，借鉴了相似理论，提出了悬移质含沙量垂线分布的统一形式，即

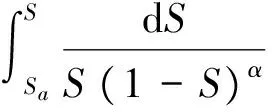
(2)

式中：n为反映固液两相特性对颗粒跳跃特征长度影响的指数；α是含沙水体中沉速公式ω=ω0(1-S)α的指数;ω0为清水中泥沙沉速。

式(2)可以描述Ⅰ型(含沙量自水面向河底先小到大，再由大变小，在河底不远处达到最大)和Ⅱ型(含沙量自水面向河底逐渐增大)含沙量垂线浓度分布。但该文献并未能给出Ⅰ型和Ⅱ型含沙量分布划分的临界条件。

其他学者提出了如重力理论[21]、随机理论[22]、混合理论[23]等一系列理论，丰富了平衡输沙状态下悬移质浓度垂线研究成果。倪晋仁等[20]对上述理论进行了研究，认为各家理论虽有不同，但导出的公式都与扩散理论得出的公式近似，且都可以视作上述统一公式(式(2))的特殊情况。

2.2 不平衡输沙条件下悬移质含沙量垂线分布研究

水流在输沙过程中，水体的含沙量往往达不到平衡，处于次饱和或过饱和的不平衡输沙状态。二维恒定均匀流不平衡输沙条件下的泥沙扩散方程为

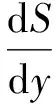
(3)

式中qs为垂线上单位面积扩散的沙量和沉降沙量的差值。

由于不平衡输沙条件下qs的调整规律目前尚无成熟的资料和研究成果，致使不平衡输沙条件下悬移质垂线浓度分布研究进展较为缓慢。

近年来，韩其为等[24]从平衡条件下的悬移质泥沙扩散方程出发，认为qs/εs与泥沙的重力作用和紊动扩散作用的对比关系及输沙的非饱和程度有关，推导出不平衡输沙条件下悬移质泥沙垂线分布公式为

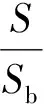
(4)

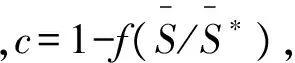
在上式中需要求得底部含沙量Sb。韩其为等[24]经分析认为在冲刷和淤积条件下Sb应当分别满足图1所示情况。

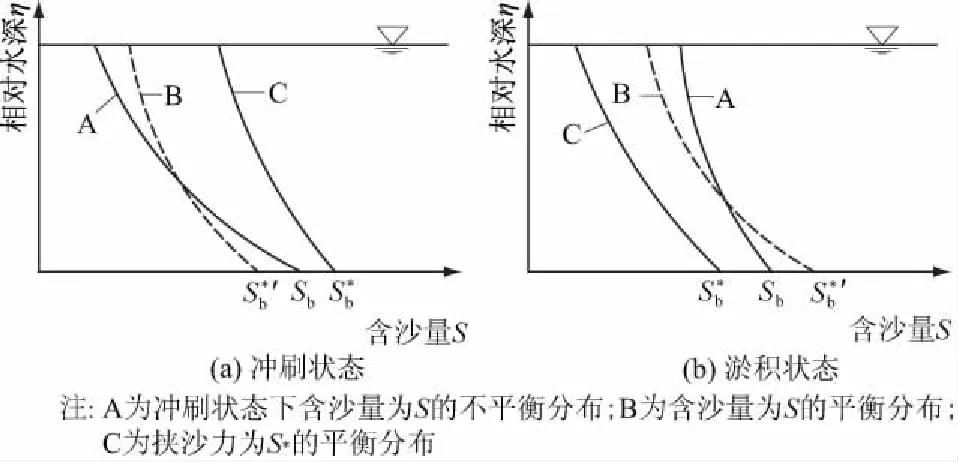
图1 含沙量垂线分布示意图

则底部含沙量Sb与Sb*′及Sb*的关系为

Sb=μSb*′+(1-μ)Sb*。

(5)

式中：Sb*′为平均含沙量垂线平衡分布底部含沙量；Sb*为挟沙能力分布底部含沙量；μ为加权系数，0≤μ≤1。

经过分析得出底部含沙量的计算式为

(6)

其中，

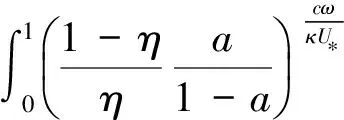
将式(6)代入式(4)得到指数形式的不平衡输沙含沙量垂线分布公式，即

(7)

韩其为开创了不平衡输沙条件下研究悬移质垂线分布的新途径，但在公式推导的过程中，引入的平均含沙量垂线平衡分布是不存在的物理量，是否合适值得商榷；其次，对悬浮指标ω/(κU*)在计算平均含沙量垂线分布和挟沙能力平衡条件下的垂线分布时采用的值相同。最后，方程虽给出了c的求解方法，但公式中加权系数μ的值如何确定也需要进一步加以研究[25]。

3 悬移质泥沙沿程恢复研究进展

水库修建后，清水下泄常引起坝下游河道长时间和长距离冲刷，在此过程中水体悬移质含沙量将沿程恢复。当前研究主要包括天然河道水沙情况实测资料研究和恢复饱和系数研究2方面内容。

3.1 实测资料研究成果

钱宁等[26]、谢鉴衡[27]认为水库下游长距离冲刷现象是由水流挟沙力沿程增加导致的，其根本原因是床沙粒径沿程变细。尤联元等[28]指出水库下游河道纵向冲刷不断下移的一个重要原因是沿程悬沙和床沙间的不断交换，冲刷距离的长短与床沙组成的沿程变化状况以及流量的大小有关。韩其为[29]认为含沙量恢复距离很长与河床组成沿程变化以及前期冲刷和其他因素导致的水力因子变化有关，并认为由于床沙组成的沿程变细，悬移质泥沙与床沙粗细颗粒之间不断的置换使悬移质级配沿程变细，引起挟沙能力沿程的缓慢增加，从而导致细颗粒泥沙发生长距离恢复。李义天等[30]根据实测资料分析指出，床沙补给不足是导致细颗粒泥沙发生长距离恢复的根本原因。

黄悦等[31]认为建库后下游河道含沙量增加的过程为含沙量的恢复过程；韩其为[32]则从含沙量与挟沙力的关系出发，认为含沙量向挟沙力靠拢的过程为含沙量的恢复过程，并认为此过程中含沙量与挟沙力始终存在一定的距离，因此这种恢复与挟沙力沿程不变条件的恢复饱和是不一样的。

卢金友[33]根据葛洲坝水利枢纽修建后实测资料分析得到，葛洲坝下游长江河道发生沿程冲刷至1994年冲刷影响已基本结束，且仅限于松滋口以上河段。陈建国等[34]分析三门峡水库下游实测资料得到，水库下游含沙量恢复的距离随水库下泄流量的增加而增加。沈磊等[35]利用实测资料分析认为，水库下游低流量级与高流量级含沙量恢复速度较快，而中水流量级含沙量恢复速度较慢。综上可见，对水库下游悬移质泥沙恢复的研究虽取得了一定的成果，但还缺少一致认可的观点，对其中一些机理的认识也有待加深。

3.2 恢复饱和系数研究成果

在实际河道冲刷计算时，常引入包含恢复饱和系数α的一维超饱和输沙方程进行计算研究，其表达式为

(8)

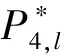
恢复饱和系数在不同研究成果中有不同的物理意义。窦国仁[36]将α解释为泥沙沉降概率，其值<1，计算式为

α=0.5+Φ(u/σ) 。

(9)

其中,

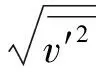
张啟舜[37]采用一定简化条件下的边界条件由立面二维扩散方程的分析解导出α恒>1。且在一定范围内，清水冲刷时α可由990.000降至3.970；淤积时，α可由1.005增至3.500。

周建军等[38]在其二维悬沙数学模型研究中，沿水深方向积分得到α的计算公式为

α=R/4+β12/R。

(10)

式中：β1为加权因子；R为Rouse数。

韩其为[39]认为α是河床近底泥沙含量与垂线平均含沙量的比值。还有研究[40]认为在水流条件一定的情况下含沙量处于次饱和、饱和、超饱和状态时的垂线平均含沙量差别较大，而底部含沙量差别较小，因此对应的恢复饱和系数的值也不同。韩其为[39]建议α在淤积时的经验取值为0.25，冲刷时取1。陆永军[41]建议冲刷时α=1.5，淤积时α=1.0。对于黄河等输沙为细沙的河流来说，因泥沙的有效沉速更小，使得α的取值更小。黄河水利科学研究院梁国亭模型[42]认为α的取值必须由河段实测资料率定得到。梁国亭根据资料率定出黄河小北干流在淤积时α为0.01，冲刷时为0.02；洛河淤积时α为0.1，冲刷时为0.3；渭河淤积时α为0.1，冲刷时为0.5。清华大学王兴奎模型[42]取α的值为0.25。

刘金梅等[43]在研究床沙粗化对不平衡输沙的影响过程中认为若假定床沙组成不变，对中沙和细沙，α分别取4.63和3.84；考虑表层床沙细化后，α取0.9和0.6(Vsy=0.6 mm/min)或0.6和0.4(Vsy=0.4 mm/min)，其中Vsy为床沙交换速率。其后刘金梅等[44]基于其所建立的不平衡输沙立面二维数学模型，计算了不同情况含沙量扩散恢复过程，总结了冲刷时恢复饱和系数的预报公式和变化规律。

在沉沙池设计中，研究人员基于一维超饱和输沙方程，通过分析实测资料得到了一系列成果。

赵志贡等[45]基于数学分析，论证了一维超饱和输沙法恢复饱和系数α与准静水沉降法修正系数K互为倒数，建立了恢复饱和系数与水流挟沙力的联系。引黄济青沉沙池设计中[46]以泥沙粒径划分α的取值：当d>0.03 mm时，α=0.072；d<0.03 mm时，α=0.170。

相关学者[47-52]分析实测泥沙资料，拟合了适合不同泥沙条件下恢复饱和系数α的计算式，可以概括为恢复饱和系数与水流紊动条件、泥沙沉速、比降等因素相关，其通用形式可以归纳为

αl=KJa(ω/U*)b(1/S0,l)c。

(11)

式中：K为综合经验系数；a，b，c均为待定系数；J为比降；S0,l为第l组泥沙含沙量。

黎运棻[47]根据大禹渡、打渔张、禹门口、人民胜利渠等沉沙池实测资料，分析得到

αl=6.644×10-5J-0.61(ω/U*)-0.62。

(12)

相关学者对非均匀悬移质恢复饱和系数的研究也取得了一定成果。葛华[53]研究了三峡水库蓄水后荆江河段的实测水沙资料，认为水库下游非均匀沙恢复饱和系数的数量级可达10-3～10-1，且一般随着泥沙粒径增大而减小，随河床冲刷历时的增加和床沙粗化程度提高而呈递减趋势。黄仁勇等[54]在对三峡库区初期运用的研究中对不同粒径组的恢复饱和系数进行了研究。张红武等[7]通过引入泥沙非饱和系数和附加系数的概念，对分组沙河床变形方程进行改造，给出了平衡含沙量(相对于恢复饱和系数)的理论计算公式。韦直林等[55]认为恢复饱和系数反映了各种因素对河床变形速率及含沙量恢复饱和速率的影响，给出了分组沙恢复饱和系数的经验关系式。

近期韩其为等[56]分析了扩散方程常见的6种边界条件[24]，基于泥沙运动随机理论提出了底部恢复饱和系数的概念，认为恢复饱和系数是底部恢复饱和系数和>1的含沙量分布系数的乘积，并建立了非均匀沙不平衡输沙时的恢复饱和系数表达式,即

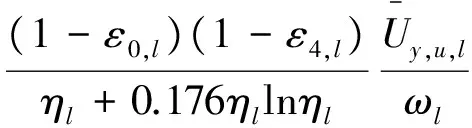
(13)

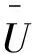
4 研究存在的问题与展望

4.1 存在的问题

综上所述，当前对水库下游悬移质泥沙沿程恢复研究取得了一定的成果，其中部分已应用于工程实践，但仍然存在若干关键问题与困难有待解决与克服。

(1) 悬移质泥沙恢复过程情况复杂，研究难度较大。平衡输沙条件下的悬移质浓度垂线分布研究已积累较多成果，但不平衡输沙条件下的相关研究成果尚少，也有待实际应用的检验。

(2) Rouse公式及其相关改进公式是基于二维恒定流均匀流假定得到的，而实际水流情况通常不能满足假定条件。其次，Rouse公式研究对象虽然是悬移质泥沙，但床沙是否均匀、是否有粗化过程或不同粒径的隐蔽-暴露作用都会影响到Rouse公式用于某单一粒径组时的准确性。

(3) 针对恢复饱和系数的研究仍有关键问题待解决。从理论研究看，一维超饱和输沙方程带有特殊性，也存在难以满足实际水流条件的情况；从已有水文资料研究看，各条河流的水流条件千差万别，也不一定完全满足假定条件，泥沙输运过程也就无法用简化条件下得到的参数准确表达出来，从而导致各家得出的恢复饱和系数α值差别较大。

(4) 相关数据的获取和分析还有待加强。前期研究虽积累了大量天然河道实测资料，但与资料对应时刻的实际冲淤情况并不都清楚。同时受限于挟沙力研究水平，当时的含沙量与挟沙能力的差别也难以给出确切的判断。天然河道水沙过程的研究，限于量测技术原因，对垂线含沙量分布情况(特别是近底处泥沙浓度)、河道来沙过程和冲淤变化情况也暂时无法直接进行实时测量，获取数据的精度也有待提高。

4.2 展 望

在未来研究中为克服上述不足，应从以下几个方面开展研究工作。

(1) 收集翔实的实测水文资料。对天然河道实测资料的分析有助于了解来水来沙情况，更好地分析掌握河道冲淤变化规律。

(2) 开展全面、系统、精确的水槽试验研究。水槽试验影响因素相对可控，能够进行单一变量变化下的试验研究。应开展均匀沙和非均匀沙条件下次饱和(并区分床沙有无补给情况)、超饱和、平衡输沙等来沙条件下的水槽试验，获取不同工况组合时的测量数据。此外在水槽试验的基础上如能开展水动力条件更加复杂的悬移质输沙试验并得到相关数据，可能对悬移质含沙量沿程恢复理论研究的推进大有裨益。

(3) 采用先进测量仪器，获取更为精确的测量数据。试验中应当尽可能多地使用先进可靠的量测仪器，尽可能多地布设测量点。测量流速、垂线泥沙浓度尤其是近底泥沙浓度的仪器精度应尽可能高且有实时监测的功能。通过设计合理的试验方案和精准可靠的测量手段，对比分析不同工况下的试验数据，以构建相关物理参数表达式，建立不平衡输沙条件下悬移质泥沙沿程分布研究的理论体系。

5 结 语

水库下游悬移质泥沙沿程恢复研究对推动河流动力学发展、解决实际工程建设面临的相关问题具有重要意义。目前对不平衡输沙条件下的悬移质浓度垂线分布和沿程分布的研究均取得了一定的成果，部分已应用于实践。但限于实测资料的可靠性和量测手段的不足，仍有众多问题有待解决。要突破研究瓶颈，应当开展系统、科学、精确的水槽试验研究，配合先进的测量仪器来获取翔实可靠的数据，以利于建立悬移质泥沙沿程恢复研究的理论体系。

[1] 张瑞瑾.河流泥沙动力学[M]. 北京:水利水电出版社, 1989.

[2] 水利水电科学研究院河渠研究所. 官厅水库建成后永定河下游的河床演变[M]. 北京：水利电力出版社, 1960.

[3] 潘庆燊, 曾静贤, 欧阳履泰. 丹江口水库下游河道演变及其对航道的影响[J]. 水利学报, 1982，(8)：56-65.

[4] ROUSE H. Modern Conceptions of the Mechanics of Fluid Turbulence[J]. Angewandte Chemie International Edition, 1937, 51(9):2124-2128.

[5] 陈永宽. 悬移质含沙量沿垂线分布[J]. 泥沙研究, 1984, (1)：33-42.

[6] 冷 魁,王明甫.明渠高含沙水流含沙量沿垂线分布的试验研究[J]. 泥沙研究,1989,(1)：8-16.

[7] 张红武,江恩慧.黄河高含沙洪水模型的相似率[M].郑州:河南科技出版社, 1994.

[8] LANE E W, KALINSKE A A. Engineering Calculations of Suspended Sediment[J]. EOS Transactions American Geophysical Union, 1941, 22(3):603-607.

[9] CHIU C L, JIN W, CHEN Y C. Mathematical Models of Distribution of Sediment Concentration[J]. Journal of Hydraulic Engineering, 2000, 126(1):16-23.

[10] VANONI V A. Transportation of Suspended Sediment by Water[J]. American Society of Civil Engineers, 1946, 111(6):67-102.

[11] RIJN L C V. Sediment Transport, Part II: Suspended Load Transport[J]. Journal of Hydraulic Engineering, 1984, 110(11):1613-1641.

[12] 王兆印, 钱 宁. 粗颗粒高含沙两相紊流运动规律的实验研究[J]. 中国科学, 1984, 27(8): 766-773.

[13] 倪晋仁, 梁 林. 水沙流中的泥沙悬浮(Ⅱ)[J]. 泥沙研究, 2000，(1):13-19.

[14] 倪晋仁, 惠遇甲. 悬移质浓度垂线分布的各种理论及其间关系[J]. 水利水运工程学报, 1988, (1): 83-97.

[15] RICHARDSON J F, ZAKI W N. Sedimentation and Fluidisation: Part I[J]. Chemical Engineering Research & Design, 1997, 75(Supp.):35-53.

[16] 张小峰, 陈志轩. 关于悬移质含沙量沿垂线分布的几个问题[J]. 水利学报, 1990, (10): 41-48.

[17] EINSTEIN H A, CHIEN N. Second Approximation to the Solution of the Suspended Load Theory[R].Berkeley: University of Caliafomia,1954.

[18] MONTES J S, ARTHUR T I. Interaction of Two-Dimensional Turbulent Flow with Suspended Particles[M]. Massachusetts: School of Engineering, Massachusetts Institute of Technology, 1973.

[19] 谢鉴衡, 周履泰. 关于扩散理论含沙量沿垂线分布的悬浮指标[J]. 武汉水利电力学院学报, 1981, (3): 1-9.

[20] 倪晋仁, 王光谦, 张红武. 固液两相流基本理论及其最新应用[M]. 北京:科学出版社, 1991.

[21] 张瑞瑾. 论重力理论兼论悬移质运动过程[J]. 水利学报, 1963, (3):13-25.

[22] YALIN M S. On the Distribution of Sediment in a Two-dimension Flow over a Mobile Bed[C]∥Stochastic Hydraulics: Proceedings of the First International Symposium on Stochastic Hydraulics. Pittsburgh, PA: University of Pittsburgh, May 31—June 2, 1971.

[23] MCTIGUE D F. Mixture Theory for Suspended Sediment Transport[J]. Journal of the Hydraulics Division, 1981, 107(6):659-673.

[24] 韩其为, 陈绪坚, 薛晓春. 不平衡输沙含沙量垂线分布研究[J]. 水科学进展, 2010, 21(4): 512-523.

[25] 赵连军, 吴国英, 王嘉仪. 不平衡输沙含沙量垂线分布理论研究展望[J]. 水力发电学报, 2015,34(4):63-69.

[26] 钱 宁, 张 仁. 河床演变学[M]. 北京：科学出版社, 1987.

[27] 谢鉴衡. 河床演变及整治[M]. 北京：水利水电出版社，1997.

[28] 尤联元，金德生. 水库下游再造床过程的若干问题[J]. 地理研究, 1990，9(4):38-48.

[29] 韩其为. 水库淤积[M]. 北京：科学出版社, 2003.

[30] LI Yi-tian, CHEN Fei. Non-uniform Sediment Transport Downstream from Reservoir[J].Transactions of Tianjin University,2008,14(4):263-270.

[31] 黄 悦, 黄煜龄. 三峡水库下游河床冲刷趋势探讨[J]. 长江科学院院报, 1998，15(3):7-10.

[32] 韩其为. 三峡水库运行后城汉河段会只淤不冲吗?—对“关于三峡工程对城陵矶防洪能力影响有关研究的讨论”的讨论[J]. 水利发电学报, 2006，25(6):79-90.

[33] 卢金友.荆江三口分流分沙变化规律研究[J]. 泥沙研究, 1996，(4)：54-61.

[34] 陈建国,周文浩,袁玉萍. 三门峡水库典型运用时段黄河下游粗细泥沙的输移和调整规律[J].泥沙研究, 2002，(2)：15-22.

[35] 沈 磊，姚仕明，卢金友.三峡水库下游河道水沙输移特性研究[J]. 长江科学院院报, 2011，28(5)：75-82.

[36] 窦国仁. 潮汐水流中的悬沙运动及冲淤计算[J]. 水利学报, 1963，(4)：15-26.

[37] 张啟舜. 明渠水流泥沙扩散过程的研究及其应用[J]. 泥沙研究, 1980, (1): 37-52.

[38] ZHOU Jian-jun, LIN Bing-nan. 2-D Mathematical Model For Suspended Sediment—PartⅠ：Model Theories and Validations[J]. Journal of Basic Science and Engineering, 1995, 3(1): 78-97.

[39] 韩其为. 非均匀悬移质不平衡输沙的研究[J]. 科学通报, 1979, 24(17): 804-808.

[40] 赵明登, 李义天. 二维泥沙数学模型及工程应用问题探讨[J]. 泥沙研究, 2002，(1):66-70.

[41] 陆永军, 袁美琦. 潮汐河口二维动床紊流模型[J]. 水科学进展, 1998, 9(2): 151-158.

[42] 钱意颖,曲少军,曹文洪，等. 黄河泥沙冲淤数学模型[M]. 郑州：黄河水利出版社, 1998.

[43] 刘金梅,王士强.河流冲刷过程中表层床沙粗化对不平衡输沙的影响[J].水科学进展,2000,11(3):229-234.

[44] 刘金梅, 王光谦, 王士强. 沙质河道冲刷不平衡输沙机理及规律研究[J]. 水科学进展, 2003, 14(5): 563-568.

[45] 赵志贡, 荣晓明. 沉沙池设计中恢复饱和系数α计算模型研究[J]. 灌溉排水学报, 2005, 24(5): 60-62.

[46] 山东省水利勘测设计院.水电站沉沙池悬移质泥沙分组沉降计算[R].济南：山东省水利勘测设计院，1993.

[47] 黎运棻. 沉沙池沿程分组悬移质含沙量变化的基本计算式及αi值[J]. 山西水利科技, 2005, (3): 5-7.

[48] 张应龙. 荆江放淤实验工程实测资料分析[J]. 泥沙研究, 1981, (3): 82-90.

[49] 杨晋营. 沉沙池超饱和输沙法恢复饱和系数研究[J]. 泥沙研究, 2005, (3): 42-47.

[50] 彭嘉玉, 姜乃迁. 黄河小北干流放淤中泥沙恢复饱和系数研究[J]. 人民黄河, 2011, 33(6): 30-31.

[51] 吴 均, 刘焕芳, 宗全利，等. 一维超饱和输沙法恢复饱和系数的对比分析[J]. 人民黄河, 2008, 30(5): 25-27.

[52] 史传文, 罗全胜. 一维超饱和输沙法恢复饱和系数α的计算模型研究[J]. 泥沙研究, 2003, (1): 59-63.

[53] 葛 华. 水库下游非均匀沙恢复饱和系数特性[J]. 武汉大学学报(工学版), 2011, 44(6): 711-714.

[54] 黄仁勇, 李 飞, 张细兵. 三峡水库运用初期库区水沙输移数值模拟[J]. 长江科学院院报, 2012, 29(1): 7-12.

[55] 韦直林，赵良奎.黄河泥沙数学模型研究[J].武汉大学学报(工学版),1997，(5):21-25.

[56] 韩其为, 陈旭坚. 恢复饱和系数的理论计算方法[J]. 泥沙研究, 2008, (6): 8-16.

Research Advances in Recovery of Suspended SedimentConcentration Downstream of a Reservoir

HE Fang-zhou1,2, ZHU Yong-hui1, GUO Xiao-hu1, CHEN Dong1

(1.Key Laboratory of River Regulation and Flood Control of Ministry of Water Resources, Yangtze River Scientific Research Institute, Wuhan 430010, China; 2.Hunan Hydro & Power Design Institute, Changsha 410007, China)

Recovery of suspended sediment concentration along the river downstream of reservoir is a core subject in river dynamics research. The research in this area helps to push the advances of river dynamics and solve problems in engineering application. In this article, the research achievements of vertical distribution of sediment concentration under equilibrium and non-equilibrium transport conditions are summarized. The observed data of suspended sediment concentration recovery along natural channels and the research results of recovery saturation coefficient are also concluded. Research on vertical distribution of sediment concentration under non-equilibrium state is still defective. The methods of observed data acquisition and data analysis also need to be improved. Finally, scientific and systematic flume experiments with accurate measuring instruments should be conducted in further studies.

suspended sediment; non-equilibrium sediment transport; vertical distribution of sediment concentration; coefficient of recovery saturation; research advances

2016-09-06；

2016-10-27

国家重点研发计划项目(2016YFC0402305)；国家自然科学基金重点项目(51339001)；水利部公益性行业科研专项经费项目(201401011)；中央级公益性科研院所基本科研业务费项目(CKSF2017041/HL，CKSF2016268/HL)；“十二五”国家科技支撑计划课题(2013BAB12B02)；国家自然科学基金青年科学基金项目(51609011)

贺方舟(1991-)，男，湖南衡阳人，助理工程师,硕士，研究方向为水力学及河流动力学，(电话)13507425895(电子信箱)hfzwenming@qq.com。

10.11988/ckyyb.20160909

TV142.3

A

1001-5485(2017)12-0001-06

(编辑：黄 玲)