一种改进的电力线通信OFDM自适应比特分配算法
2017-12-20吴素园李玲欣
申 敏,吴素园,李玲欣
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.重庆邮电大学 新一代宽带移动通信重点实验室,重庆 400065)

一种改进的电力线通信OFDM自适应比特分配算法
申 敏1,2,吴素园1,李玲欣1
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.重庆邮电大学 新一代宽带移动通信重点实验室,重庆 400065)
针对低压电力线信道的频率选择性衰落等特点,在总功率和峰值功率限制下提出一种低复杂度的自适应比特分配算法。该算法首先对子载波进行分组以降低计算复杂度,组内子载波将采用相同的调制方式。然后采用注水算法解决连续比特输入问题,将其得到的位向量取整后作为贪婪算法的初始比特分配向量,证明了位向量的有效性。根据得到的初始向量在每个子载波上进行比特增加贪婪操作或比特移除贪婪操作。仿真结果表明从初始比特向量开始,每个子载波上最多只需进行一次比特增加或移除操作即可达到最佳吞吐量。与其他传统算法相比,在不同数量子载波、不同总功率约束等限制条件下,所提算法能在保证系统吞吐量的同时使其计算复杂度有效降低。
电力线通信(PLC);峰值功率;比特分配;低复杂度算法
0 引 言
近年来,电力线通信(power line communication, PLC)凭借不需要额外布线的优势受到了越来越多的关注。逐渐成为智能电网、自动计量架构、家庭自动化等一些领域的研究热点[1]。如何降低设备复杂度及提高数据传输速率是当前亟待解决的问题之一。在OFDM(orthogonal frequency division multiplexing)系统中,当发送端已知信道状态信息时,可以采用自适应比特分配技术在不同限制条件下对子载波进行比特和功率分配。进而改善系统性能和提高频带利用率[2]。
目前已有许多国内外学者对低压电力线中自适应比特分配问题进行了研究探索[3-10]。文献[3]中提到的传统贪婪算法是最佳的离散比特分配,但是该算法是对每个子载波进行比特分配操作,其实现复杂度非常高。文献[4]基于turbo编码的纠错能力,利用对数似然比提出一种新的度量约束,并将其应用到脉冲噪声环境中进行比特分配。文献[5]利用电力线信道的特点,将主频周期分为多个时隙,在主频周期平均功率值一定的条件下使得每个时隙中的功率值不同,然后在此基础上进行比特分配。文献[6]给出了一种频谱压缩资源分配方案,考虑了相邻子信道之间的相关性。在有线通信系统例如ADSL(asymmetric digital subscriber line)和PLC中,为了确保与其他无线电系统的兼容性,需要考虑频谱屏蔽限制(例如峰值功率限制)。尽管上述文献研究了总功率一定下的离散比特分配问题,但是峰值功率限制问题没有被完全解决。在考虑峰值功率限制问题方面,文献[7]提出一种次优算法(sub-optimal algorithm,SOA),该方法通过补偿连续速率最大化的解给出离散速率最大化解,引入变量α使得对应于补偿后的整数比特加载所需总功率尽可能接近允许的总功率。文献[8]表明传统比特增加贪婪算法(greedy-based bit-adding, GBA)对于离散比特分配问题能产生全局最佳解,然而该算法复杂度是总功率的递增函数。文献[9]中提到在总功率和峰值功率限制下采用比特移除贪婪算法(greedy-based bit-removing, GBR),其在计算成本方面的性能是总功率的递减函数。文献[10]在功率约束限制条件下,考虑了PLC中符号间干扰与载波间干扰,提出一种新的离散比特初始化方法,但是文中没有证明其最优性。
本文在总功率和峰值功率约束下,提出一种改进的低复杂度比特分配算法。该设计思想首先对相邻子载波进行分组划分,然后通过注水算法解决相关连续比特输入速率最大化问题,将其得到的位向量取整后作为贪婪算法中的一个有效比特分配向量,并证明了该位向量的有效性,最后根据得到的初始比特向量进行比特增加贪婪操作或比特移除贪婪操作。
1 系统模型
1.1 系统结构图
低压电力线物理层如图1所示。接收端采用信道估计算法估计出子载波的信道状态信息,进而得到子载波的信噪比,通过反馈信道传递给发送端。在发送端,用于PLC数据传输的信息比特经过加扰、turbo卷积编码、交织后,根据自适应调制算法确定OFDM每个子载波不同的调制方式,并将自适应调制方式通过帧控制符号发送给接收端。
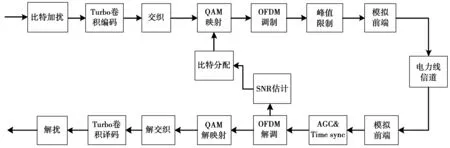
图1 PLC物理层过程框图Fig.1 Physical layer process of PLC
本文参考国家电网提出的PLC协议,OFDM调制采用1 024点离散傅里叶逆变换来实现。此外,为了遵循频率监管机构的要求,512个子载波中只有411个可用于数据传输,涵盖直流到12.5 MHz频段。为了减少接收端的复杂度,采用合适的循环前缀来消除符号间干扰(inter symbol interference,ISI)和载波间干扰(inter carrier interference,ICI)。在模拟前端模块之前,插入峰值限制模块来减少峰均功率比,最后,信号耦合到电力线信道中进行传输。在接收端,信号经过模拟前端后送入到自动增益模块和时间同步模块,本文假定这2个模块均是理想的。接着去循环前缀和进行OFDM解调,即1 024点离散傅里叶变换(discrete fourier transform,DFT)。假设循环前缀完全消除了ISI和ICI,系统可实现完全同步;然后将DFT变换后的数据送入到QAM(quadrature amplitude modulation)解映射模块,根据信道状态信息与接收到的自适应调制信令完成解调、解交织、Turbo卷积译码以及解扰,重构和估计发送比特。本文设定信道估计是理想的,且不考虑信道状态信息与自适应调制信息的传输误差。
1.2 信道模型
本文采用多径PLC信道模型进行电力线通信仿真,其传输函数为[11]
(1)
(1)式中:i代表路径数,1为最短路径;gi为路径i的加权因子;a0,a1代表衰减参数;k为衰减因子指数,典型值在0.5到1之间;di表示路径i的长度;τi表示路径i的延时。
2 自适应比特分配算法
PLC系统中每个OFDM符号上有用子载波数高达成百上千,对每个子载波进行比特分配处理会使信令负荷非常庞大。本文所提算法首先将连续子载波进行分组以降低计算复杂度,被分到同一个组中的子载波可以作为一个共同体对待,组内子载波采用相同的比特分配。算法步骤分为两部分:①对子载波进行子带划分,根据总功率和峰值功率限制给出比特分配约束条件;②由注水算法解决目标函数的解得到整数位向量作为贪婪算法的初始比特分配,然后根据得到的初始比特分配进行比特增加贪婪操作或比特移除贪婪操作。
2.1 基于子带的离散比特分配问题
设电力线OFDM系统中有用子载波总数为N,划分为L组,组内宽度n=N/L,组内子载波参考其SNR(signal noise ratio)均值SNRmean采用相同的比特分配。在峰值功率和总功率限制下最大化系统的传输速率,建立速率自适应比特分配约束条件为
(2)
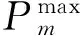
此外,有如下定义
(3)
(3)式中,⎣」表示向下取整。(3)式分别表示子带m在峰值功率限制下的最大比特数、实际所能承载的最大有效比特数以及最大有效功率的大小。故(2)式可以重写为
(4)
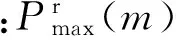
2.2 离散比特分配算法
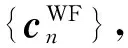
(5)
用bWFR表示WF算法得到的整数比特向量,PWFR为其对应的功率大小
(6)
通过解方程(7)得到总功率和峰值功率约束下的解[7]。
(7)
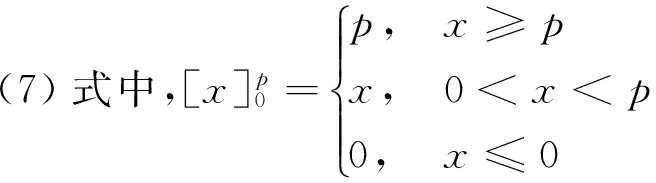
(8)
文献[3]中定义了用于比特/功率分配的有效位向量。其定义如下:若不存在这样的子载波对,使得从其中一个子载波上移除一个比特所得到的功率增量可以用于在另一个子载波上添加一个比特,则该位向量是有效的。接下来证明本文所提算法中bWFR是一个有效位向量。证明如下。
采用WF算法解决连续比特分配问题得到子载波n上功率和容量大小为
(9)
(9)式中:K1是(7)式的解,且K2=lb(K1/Γ)。
经过取整操作得到的比特数与对应的功率分配分别为
(10)

场景1:
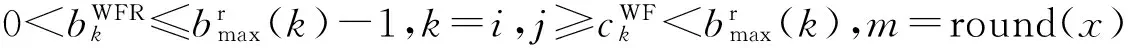
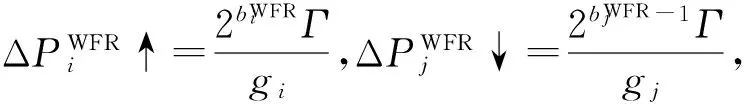
场景2:


场景3:
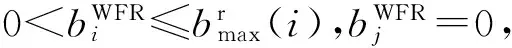
在所有情况下都不存在从某个子载波移除一个比特到另一个子载波而减少总的所需功率,故bWFR是一个有效位向量。
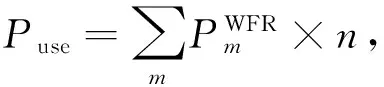
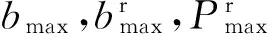
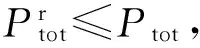
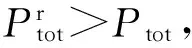
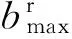
ⅱ)若Puse>Ptot,采用比特移除贪婪算法[9]在还没有达到0比特的子载波上移除比特。
3 复杂度和仿真分析
3.1 运算复杂度分析
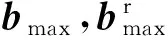

表1 算法操作次数Tab.1 Number of algorithm operations
由表1可以看出,GBA与GBR算法复杂度分别和LBA,LBR有关,而LBA随着允许的总功率增加而增加,LBR随着允许的总功率增加而减少,因此GBA与GBR算法分别是允许的总功率的递增和递减函数,且2种算法都是对每个子载波进行处理,复杂度都较高。SOA算法复杂度主要取决于Ls与Lr的大小,文献[7]中已证明该算法复杂度较传统算法有所降低。此外,本文所提算法第一步是先进行子载波分组,通过减少子载波总数降低了复杂度,然后采用文献[7]中提到的注水算法获得初始比特分配,该分配过程所需迭代次数即Ls大小,仿真结果表明初始比特分配后,每个子载波最多只需进行一次比特增加/移除操作,相较于SOA算法需要迭代找到合适的α值来实现最佳吞吐量,所提算法复杂度得到进一步降低。后续仿真结果将给出不同算法总运行时间的对比。
3.2 仿真结果分析
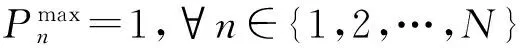

表2 仿真参数Tab.2 Simulation parameters
图2为不同分组长度下本文所提算法与GBA和GBR算法的系统平均吞吐量对比。图2中,当分组长度为2或4时,使用本文所提算法得到的吞吐量与GBA和GBR算法得到的几乎相同。随着分组长度增加,本文所提基于子带划分算法获得的吞吐量呈现减少趋势。分析可知,当组内的子载波数增加时,其确定的组内平均信噪比与各个子载波真实信噪比差异越大,导致系统性能降低,但分组长度增加减少了信道和信令信息传输次数,因此,系统复杂度也会降低。图2还表明,随着允许的总功率逐渐增大,其吞吐量呈现平缓趋势。这是因为在峰值功率限制下,一旦系统所需最大有效总功率小于或等于允许的总功率,各个子载波上分配的比特数是一个固定值,该值是其在峰值功率限制下所能达到的最大值。考虑到分组长度增加使得系统复杂度降低,本文采用分组长度为4的比特分配算法用于后面算法的对比分析。
图3和图4分别对比了4种算法下系统的吞吐量与使用的总功率。可以注意到使用本文算法得到的吞吐量与最佳分配算法得到的几乎相同(见图3),此外,由GBA算法、GBR算法与本文算法得到的比特/功率分配总是相同的(见图4),这也证实了本文算法的最优性。同时注意到SOA算法得到的吞吐量略微降低,这是由于该算法的最终比特分配取决于最后固定α所需的迭代次数。当迭代次数增加时,该算法几乎能收敛到最佳吞吐量。

图2 不同算法下系统平均吞吐量对比Fig.2 Achieved throughput comparison
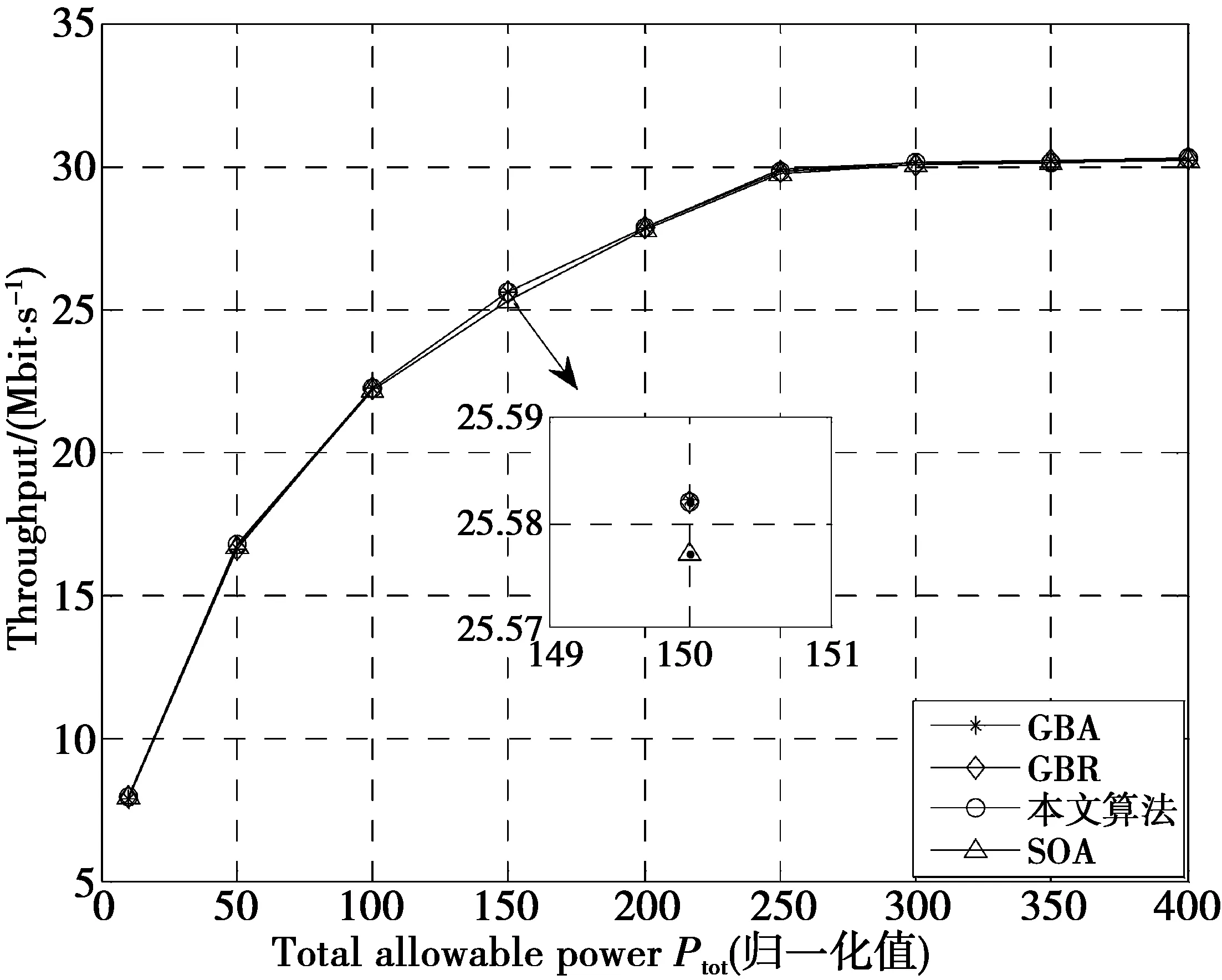
图3 不同算法下系统平均吞吐量对比Fig.3 Achieved throughput comparison
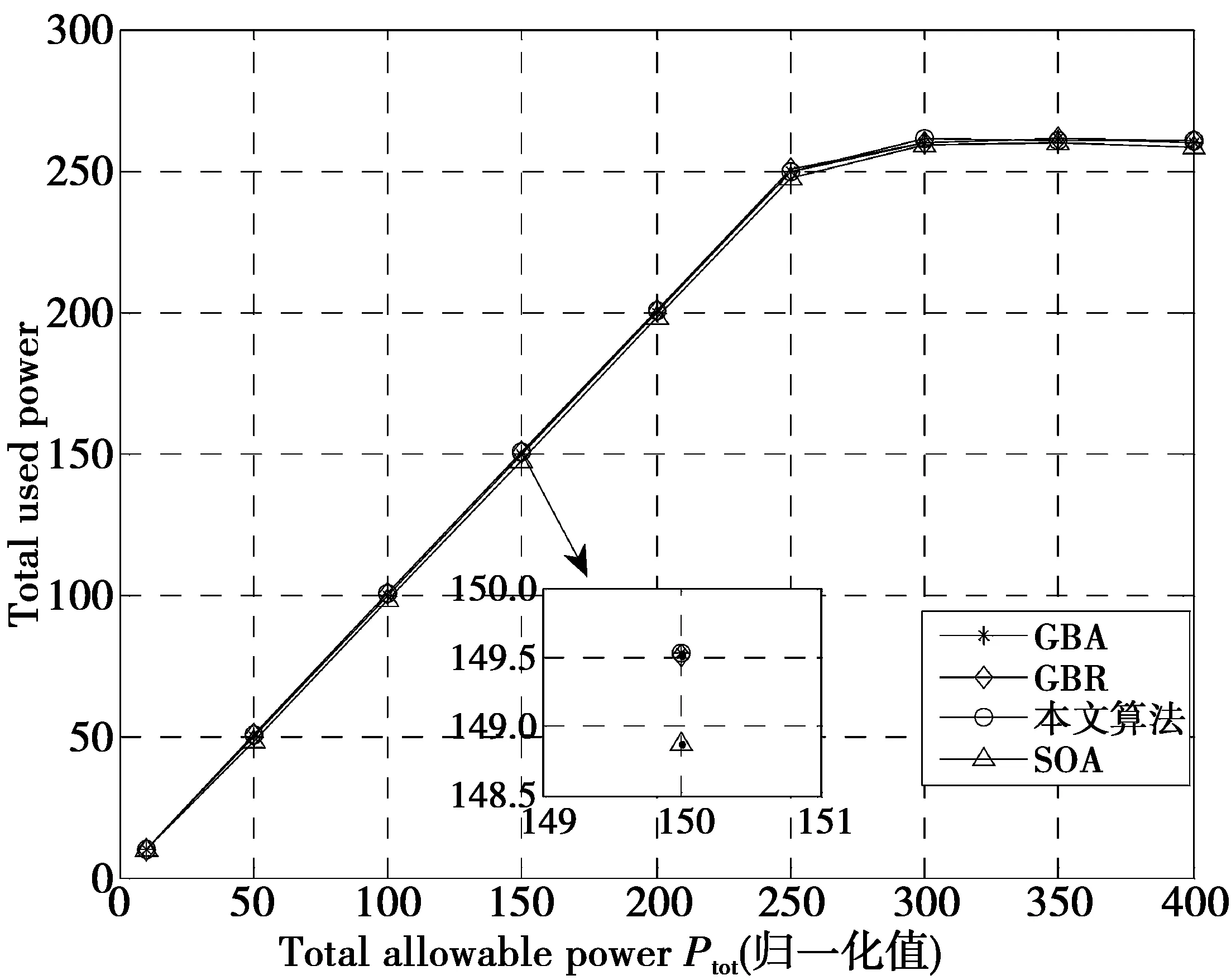
图4 不同算法下系统总使用功率对比Fig.4 Total used power comparison
图5比较了不同算法所需总运行时间,由图5中可以看出,GBA算法与GBR算法的性能指标分别是总功率Ptot的递增和递减函数。当Ptot较大时,GBR算法性能优于GBA算法性能,反之则GBA算法性能优于GBR算法性能。这是由于2种算法的初始比特分配不同导致的,GBA算法初始比特分配为0,每次迭代时在所需功率增量最小的子载波上增加1个比特。GBR算法初始比特分配为其所能达到的最大值,每次迭代时在所需功率增益最大的子载波上移除1个比特。此外,本文所提算法与SOA算法的总运行时间随着Ptot变化几乎不变,且本文算法复杂度低于SOA算法复杂度,与GBA和GBR算法相比其复杂度明显降低。

图5 不同算法下总运行时间对比Fig.5 Total run-time comparison
图6为固定Ptot为100(P0Δf归一化值)时,算法所需运行时间与子载波数分别为128,256,408间的关系。注意到本文所提算法的开销总是优于GBA,GBR与SOA算法,且随着子载波数增加,本文所提算法复杂度降低越大。从分析可知,由于GBA算法与GBR算法是对每个子载波进行处理,因此当子载波数增加时,GBA算法与GBR算法复杂度会增大。而本文所提算法第一步对子载波进行分组,降低了复杂度,又采用有效的初始位向量作为贪婪算法的初始比特分配,仿真表明,经过初始比特分配后,每个子载波上最多只需进行一次比特增加或比特移除操作,因此,随着子载波数增加,本文所提算法复杂度变化较小。
4 结束语
本文在PLC信道环境下,提出一种改进的低复杂度速率自适应比特分配算法。已证明该算法的最优性,其处理包括先对子载波进行分组操作,然后采用注水算法解决连续比特分配问题,将其得到的位向量取整后作为贪婪算法初始比特分配向量,并且证明了该位向量的有效性,其次仿真表明初始比特分配完成后,每个子载波上最多只需加载或移除一个比特。此外,本文所提算法在分组长度为4时可实现吞吐量与最优分配算法几乎相同,且在不同数量子载波、不同总功率约束等限制条件下,该算法的复杂度都较参考算法复杂度有所降低。
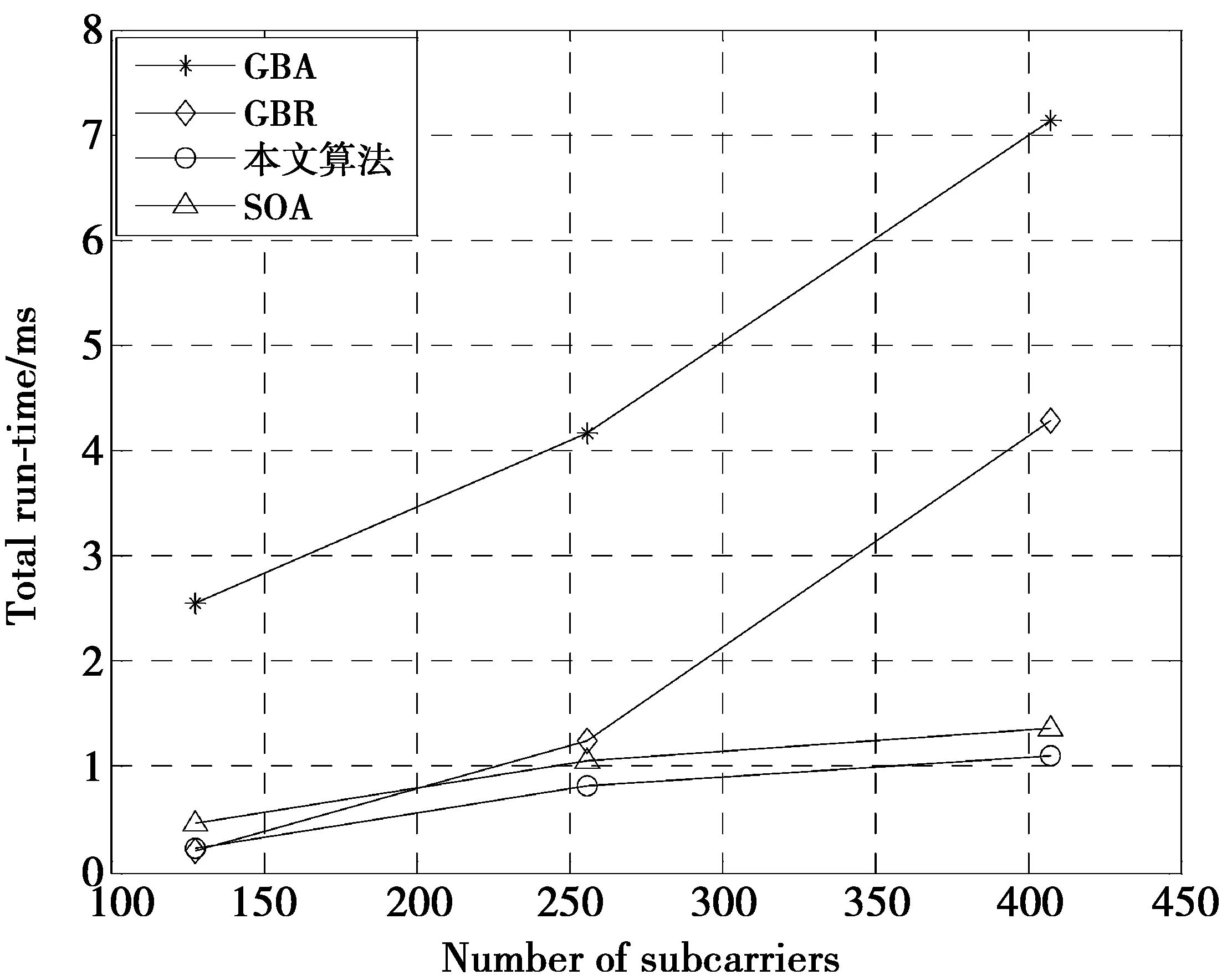
图6 不同子载波下总运行时间对比Fig.6 Total run-time vs number of subcarriers
[1] ANCILLOTTI E,BRUNO R,CONTI M.Review:The role of communication systems in smart grids:Architectures,technical solutions and research challenges[J].Computer Communications,2013,36(17-18):1665-1697.
[2] WU Z, ZHOU X, YANG Q, et al. An adaptive bitload OFDM system for Low Voltage Power Line communication[C]//Solid-State and Integrated Circuit Technology (ICSICT), 2014 12th IEEE International Conference on. Guilin: IEEE, 2014: 1-3.
[3] CAMPELLO J. Optimal discrete bit loading for multicarrier modulation systems[C]//Information Theory, 1998. Proceedings. 1998 IEEE International Symposium on. Cambridge, MA: IEEE, 1998: 193.
[4] GUERRINI E, GUERRIERI L, VERONESI D, et al. LLR-based Bit-loading Algorithm and its Applications to HomePlug AV over OPERA Power-line Channels with Impulsive Noise[J]. Journal of Communications, 2009, 4(7): 454-462.
[5] TUNC M A, PERRINS E, LAMPE L. Optimal LPTV-aware bit loading in broadband PLC[J]. IEEE Transactions on Communications, 2013, 61(12): 5152-5162.
[6] COLEN G R, OLIVEIRA L G, VINCK A J H, et al. A Spectral Compressive Resource Allocation Technique for PLC Systems[J]. IEEE Transactions on Communications, 2017, 65(2):816-826.
[7] BACCARELLI E, FASANO A, BIAGI M. Novel efficient bit-loading algorithms for peak-energy-limited ADSL-type multicarrier systems[J]. IEEE Transactions on Signal Processing, 2002, 50(5): 1237-1247.
[8] BACCARELLI E,BIAGI M.Optimal integer bit-loading for multicarrier ADSL systems subject to spectral-compatibility limits[J].Signal Processing,2004,84(4):729-741.
[9] PAPANDREOU N, ANTONAKOPOULOS T. Bit and power allocation in constrained multicarrier systems: the single-user case[J]. EURASIP Journal on Advances in Signal Processing, 2008,(1): 1-14.
[10] VO T N, AMIS K, CHONAVEL T, et al. Achievable throughput optimization in OFDM systems in the presence of interference and its application to power line networks[J]. IEEE Transactions on Communications, 2014, 62(5): 1704-1715.
[11] ZIMMERMANN M, DOSTERT K. A multipath model for the powerline channel[J]. IEEE Transactions on Communications, 2002, 50(4): 553-559.
[12] HASHMAT R, PAGANI P, CHONAVEL T, et al. Analysis and modeling of background noise for inhome MIMO PLC channels[C]//Power Line Communications and Its Applications (ISPLC), 2012 16th IEEE International Symposium on. Beijing: IEEE, 2012: 316-321.
The National Science and Technology Major Project of China(2016ZX03002010-003)
AnimprovedbitallocationalgorithmforPLC-OFDMsystem
SHEN Min1,2,WU Suyuan1,LI Lingxin1
1.School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R. China; 2. Key Lab of New Generation Broadband Mobile Communication Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R. China)
To adapt to frequency selective fading of low-voltage power line, a new low-complexity adaptive bit loading algorithm is proposed under the total power and peak power constraints. Firstly, the subcarriers are grouped to reduce the computational complexity, the subcarriers in the group will use the same modulation scheme. And then the water-filling algorithm is used to solve the related continuous-input rate maximization problem, the rounding bit vector is used as the initial bit allocation vector of the greedy algorithm, this paper theoretically proves the validity of the bit vector. Finally, according to the initial vector, greedy-based bit-adding operations or greedy-based bit-removing operations are exploited on each subcarrier. The simulation results show that the optimized throughput, starting from the initial bit vector, is achieved by adding or removing bits on each subcarrier at most once. Compared with many algorithms in the literature, the proposed algorithm can guarantee the achievable throughput with significant reduction of computation cost under the different numbers of subcarriers and different total power constraints.
power line communication(PLC); peak power; bit loading; low-complexity algorithm
10.3979/j.issn.1673-825X.2017.06.004
2016-09-11
2017-09-11
吴素园 526044828@qq.com
国家科技重大专项基金资助项目(2016ZX03002010-003)
TN915
A
1673-825X(2017)06-0732-07

申 敏(1963 -),女,重庆人,教授、博士生导师,主要研究方向为通信核心芯片、协议与系统应用技术。E-mail: shenmin@cqupt.edu.cn。
吴素园(1992 -),女,湖北荆州人,在读硕士研究生,主要研究方向为PLC系统自适应比特分配算法。E-mail: 526044828@qq.com。

李玲欣(1993 -),女,重庆人,在读硕士研究生,主要研究方向为PLC系统导频设计算法研究。E-mail: 361247104@qq.com。
(编辑:张 诚)
