MIMO系统中基于条件数阈值的格基约减信号检测算法
2017-12-20周围,曾雪,樊鹏
周 围,曾 雪,樊 鹏
(1.重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065; 2.重庆邮电大学 光电工程学院,重庆 400065)

MIMO系统中基于条件数阈值的格基约减信号检测算法
周 围1,2,曾 雪1,樊 鹏2
(1.重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065; 2.重庆邮电大学 光电工程学院,重庆 400065)
在多输入多输出系统中,最大似然(maximum likelihood,ML)检测算法性能最优但复杂度很高,最小均方误差(minimum mean-square error, MMSE)检测算法复杂度低但其性能较差。较高的信道矩阵条件数会给信号检测算法的误码率性能带来不利影响。针对这些问题,提出一种基于信道矩阵条件数阈值的信号检测算法来提升高条件数下传统检测算法的性能。该算法通过比较信道矩阵的条件数与预先设定的条件数阈值,选取相应的检测算法:当条件数低于阈值时,采用复杂度较低的LLL(lenstra-lenstra-lovasz)约减的MMSE(LLL-MMSE)算法来减少计算量;当条件数高于阈值时,采用基于排序分组的ML与LLL-MMSE联合的检测算法,通过增加一定的计算量来保证检测性能。对不同阈值下的误码率性能进行了仿真,结果表明算法的性能明显优于传统的LLL-MMSE检测算法,并且通过预先设定条件数阈值可以使得算法在性能和复杂度之间获得较好的平衡,最终达到优化检测算法性能的目的。
多输入多输出;格基约减;矩阵条件数;阈值;LLL
0 引 言
在多输入多输出(multiple-input multiple-output,MIMO)无线通信系统中,最大似然(maximum likelihood,ML)[1]信号检测算法的检测性能是最优的,但是由于该算法的复杂度会伴随着并行传输符号数以及信号星座规模的增加而呈现出指数增长关系,因而在许多实际环境中是无法实现的。线性检测算法中的迫零(zero-forcing, ZF)[2]检测算法及最小均方误差(minimum mean-square error, MMSE)[3]检测算法尽管具有较低的计算复杂度,但因其不能达到全分集,在性能上与最优检测有较大的差距。格基约减(lattice reduction,LR)[4]算法是一种能够对信道矩阵进行预处理的算法,将其与其他算法相结合,不仅可以很好地提升检测算法的性能,而且能明显降低算法的复杂度。在现有的格基约减算法中,LLL(lenstra-lenstra-lovasz)算法[5]能够使矩阵条件数得到有效降低,故在线性检测时,可以通过利用LLL算法来达到有效降低信道矩阵的条件数的目的,以此来提高算法的检测性能。
另一方面,当信噪比较高时,信道矩阵的条件数[6]会对MIMO系统的容量产生决定性的影响;而当信噪比相同时,信号的检测性能也会因不同的信道矩阵而产生十分明显的差别。文献[7]中提出一种基于矩阵条件数阈值的格基约减辅助K-best信号检测算法,该算法在信道状态较好,即信道矩阵条件数较小的情况下不使用格基约减算法,只有在信道状态较差,即条件数大于设定阈值的情况下,才使用格基约减来降低矩阵条件数,可以在对检测算法性能没有过大影响的前提下显著地降低因采用格基约减而带来的额外计算复杂度。文献[8]提出一种带约束条件的LLL格基约减检测算法,虽然这种算法在接近最优检测(ML检测)性能基础上,能够有效地降低算法的计算复杂度,但是在信道矩阵条件数较低时,即信道条件状态良好的条件下,仍然存在计算冗余这一现象。鉴于此,本文提出了一种新的基于条件数阈值的检测算法,其核心思想是:在已知信道状态的无线MIMO系统中,当信道矩阵条件数较低时,在接收端使用基于LLL约减的MMSE(LLL-MMSE)信号检测算法;而当信道矩阵条件数较高时,在接收端采用基于排序分组的ML和LLL-MMSE联合的信号检测算法。该方法能够保证在条件数较小时,采用简单的算法从而使计算复杂度有效降低;当条件数较高时,通过增加一定的计算量来保证系统的检测性能,从而使得算法在性能和复杂度之间获到较好的平衡,最终达到优化检测算法的目的。
1 MIMO系统信号模型
MIMO系统结构框图如图1所示。对于一个MIMO系统,其发射天线数为Nt,接收天线数为Nr,那么系统信号模型可表示为
y=Hx+n
(1)
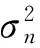
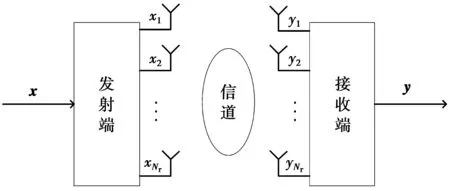
图1 MIMO系统结构框图Fig.1 MIMO system model
2 传统检测算法
2.1 最大似然检测算法
ML算法是对星座图中所有的节点进行遍历搜索,因此,具有较高的可靠性,且该算法性能最优。该算法的检测原理是:先推算出接收信号与所有可能的发射信号值之间的欧式距离,找到其中最小的欧式距离并将其所对应的发射信号值当做是对原始发射信号x的估计值,其原理表达式为
‖y-Hx‖2
(2)
(2)式中:Ω表示在系统发射端所采用的调制方式下由全部的发射符号构成的集合;‖·‖2表示对向量进行取二范数操作。
2.2 最小均方误差检测算法
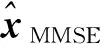
‖Gy-x‖2}
(3)
(3)式中,E{·}表示取{·}的统计平均。
MMSE检测算法的加权矩阵为
GMMSE=(HHH+σ2I)-1HH
(4)
(4)式中:I表示Nt×Nt维的单位矩阵;σ2=E[|ni|2]表示噪声功率。
将加权矩阵GMMSE和接收信号y相乘可得
(5)
滤波后,即进行硬判决得到信号的估计值
(6)
(6)式中,Q(·)表示硬判决运算。
3 格基约减
设b1,b2,…,bm∈n为一组线性无关的向量,其中,n表示复数域上的n维向量空间。集合表示以(b1,b2,…,bm)为基的格,其中,m称为格的维数。若m=n,则格L称为满秩的[9]。如果=Z,即格中元素取自于复整数环,则称之为整格。一个格可以用不同的基来表示。格基约减就是在对格上的问题进行处理时,争取找到符合一定条件的一组基以便于解决相关的问题,这组基就表示为格的一组约减基。格基约减的基本原理[10]如(7)式所示
H′=HT
(7)
(7)式中:H′是一个长度更短而且正交性更好的矩阵,利用矩阵T对矩阵H进行转化。在初始化时,定义单位矩阵T,进行格基规约,因为T是幺模矩阵,H的维数没变化,相当于对H进行了列初等变换。在MIMO系统中对信道矩阵H进行LLL约减,即对H进行QR分解(H=QR)后可得上三角矩阵R,进行满足(8)式和(9)式2个条件的约减,其中,rk,l为R的第k行第l列元素。
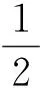
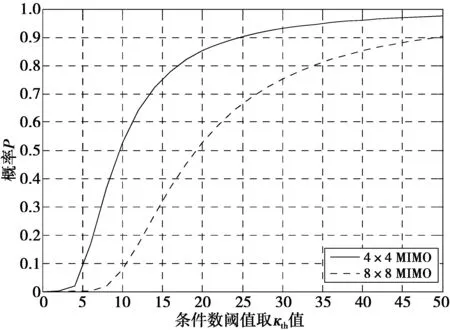
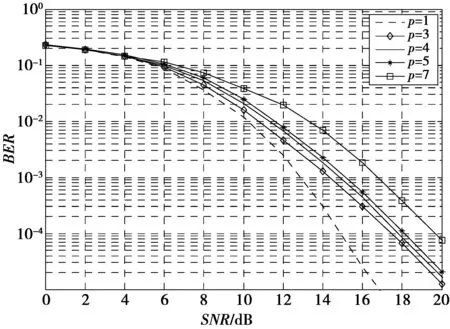
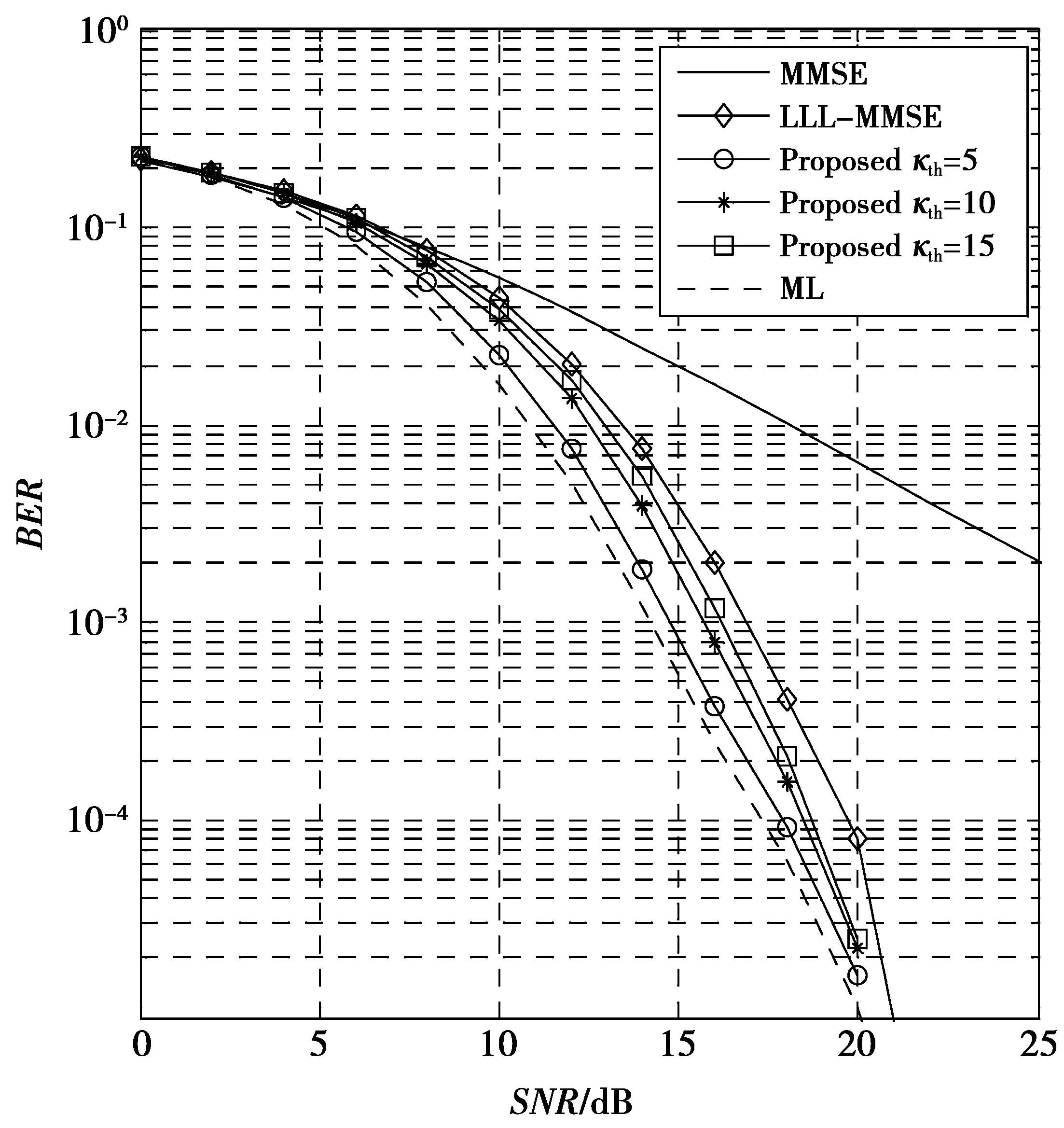
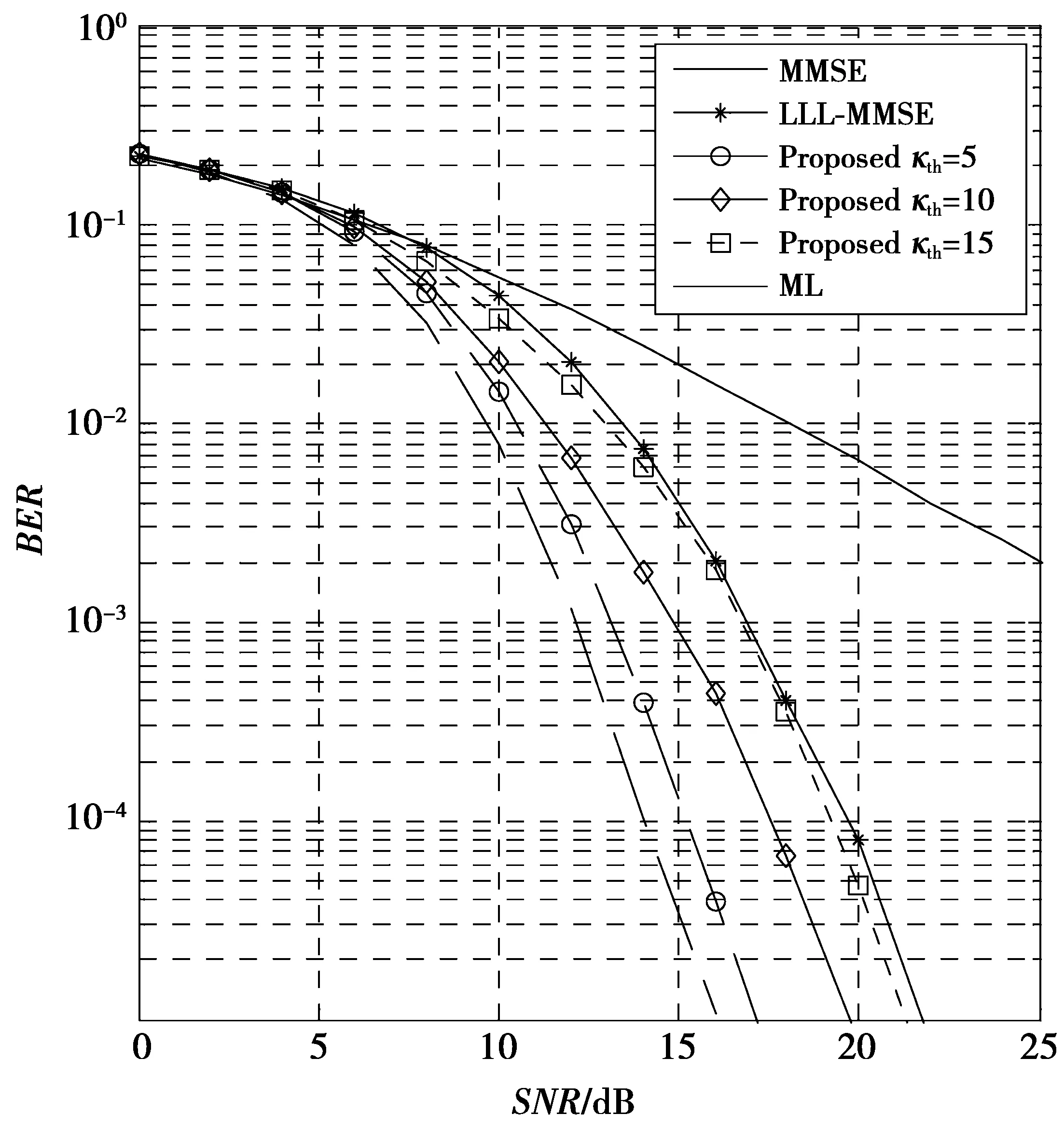
1≤k (8) δ|rl-1,l-1|2≤|rl,l|2+|rl-1,l|2, l=2,…,Nt(1/4<δ≤1) (9) 则可称H是满足参数δ的LLL约减,并且通过LLL约减得到的新基H′与原始格基H相比具有更低的条件数,即格基约减可以降低矩阵的条件数。图2 是4×4矩阵在格基约减前后的条件数的概率密度函数分布图。可以看出,经过格基约减后的信道矩阵,其条件数较小的概率远远大于大条件数的概率,即经过格基约减后的MIMO系统信号检测性能会有所改善。 图2 概率密度函数分布Fig.2 Probability density function distribution 文献[11]中给出了对于限定条件为Nt=Nr的情况下,信道矩阵条件数的概率密度函数公式为 (10) (10)式中,κ表示信道矩阵条件数。 本文提出的改进算法利用了LLL算法降低信道矩阵条件数来提升线性算法检测性能的特性,结合条件数阈值κth来选择不同的算法:当κ大于κth时,使用基于排序分组的ML /LLL-MMSE联合的算法;当κ小于κth时,采用LLL-MMSE算法。其发送信号的估计如(11)式 (11) Pr{κ>κth}=1-pκth (12) (12)式中:pκth表示选取基于LLL-MMSE算法的概率,也表明本文算法同LLL-MMSE算法的复杂度相等的概率。(12)式中Pr{κ>κth}=1-pκth取决于κ的分布。根据(10)式,对于限定的条件Nt=Nr,由条件数概率密度函数公式可得 (13) 即条件数阈值的累积概率为 (14) 由(14)式可推出条件数阈值的表达式为 (15) MIMO系统中信号检测性能受信道矩阵条件数的影响很大,而LLL算法作为一种检测前的预处理方法能够有效地降低信道矩阵的条件数,能够改善条件数较大时格基约减算法的检测性能。本文提出基于排序分组的ML /LLL-MMSE联合的检测算法,用来提升LLL算法的性能。具体算法步骤如下。 1)分组:计算矩阵H每一列的二范数,依据每列的二范数大小降序排序,划分为H1,H22个子矩阵,有y=Hx+n=H1x1+H2x2+n; 2)ML:遍历x2的所有可能性,假设有M种可能性; 4)判决:将所检测出的x1及x2的结果相结合,可以得到关于x解的集合xm,m=1,2,…,M,最后通过欧氏距离判决。 首先对矩阵H=[h1,h2,…,hNt]的每一列进行二范数计算,并且按照每列的二范数大小降序排序,假设‖h1‖2≥‖h2‖2≥…≥‖hP‖2≥‖hP+1‖2≥…≥‖hNt‖2。信道列向量的二范数的大小与信道的质量成正比,当二范数大,即信道的质量越好,此时应当选取LLL-MMSE检测算法;当二范数小,即信道的质量越差,此时应当选取ML检测算法。将信道矩阵分为子矩阵H1和子矩阵H2,对子矩阵H1的选取步骤如下。 1)所有可能的Nr×P维子矩阵集合记为HP,其中,P≤Nt; 2)对集合HP里面的矩阵进行LLL约减,可以得到相应的约减基集合,记为BP; (16) (16)式中:P为格生成矩阵B的列数;bi为格生成矩阵B的第i列;det(·)表示对(·)执行取行列式操作。对于格生成矩阵B而言,有0≤δ(B)≤1; 子矩阵H2就是在信道矩阵H中去除子矩阵H1中的列后所得矩阵。 对本文算法的检测性能进行仿真:假定收发端相互独立,接收端已经理想同步且信道状态信息为已知,用户的发射功率为1,传输中的每个噪声均为服从均值为0的独立同分布加性高斯白噪声,信道模型采用瑞利信道,仿真次数为105次,考虑条件数阈值为κth=5,κth=10和κth=15。图3是在8×8 MIMO中采用QPSK调制方式且κth=10时,对参数P={1,3,4,5,7}取不同值时的检测算法性能对比图,可以看出,参数P越小,算法的检测性能越好,反之参数P越大,算法的检测性能越低。然而当性能越好时,复杂度随着P的减小而大幅度增大,所以本文在此基础上选择P=Nt/2来对算法的复杂度和性能进行一个平衡,并对算法的性能进行仿真。 图3 不同参数P的检测算法误比特率Fig.3 BER performance of different parameters P 图4和图5分别表示为4×4 MIMO系统中采用QPSK调制方式下的不同检测算法性能比较和8×8 MIMO系统中采用QPSK调制方式下的不同检测算法性能比较,图6所示为4×4和 8×8 MIMO系统中选取LLL-MMSE检测算法的概率,通过分析不同MIMO系统中各检测算法误码率性能仿真图(图4、图5)可知:本文算法检测性能较传统MMSE算法检测性能而言有了显著的改善;同时,在相同的天线配置数目的MIMO系统中,条件数阈值的设定越小,即对信道质量的要求越高,系统的性能就会越好。图6表示在不同的MIMO系统下选取LLL-MMSE算法的概率,由图6可知:在天线配置相同的条件下,增大条件数阈值的同时选取LLL-MMSE检测算法的概率也随之增加。这表明了在低信道矩阵条件数下,即信道质量较好的情况下选择LLL-MMSE检测算法;反之,在高信道矩阵条件数下,即信道质量较差的情况下,使用基于排序分组的ML/LLL-MMSE联合的检测算法。即条件数阈值越小,采取基于排序分组的ML/LLL-MMSE联合的检测算法的概率就越大,算法复杂度增加,性能也越好。因此,在实际中对条件数阈值的选取,可根据不同业务类型(如语音、图像、数据等)对误码率的要求进行抉择。首先由所要求误码率的高低决定选取LLL-MMSE算法的概率pκth,再通过pκth由(15)式或图6选取相应的条件数阈值κth。 图4 4×4MIMO中各检测算法误比特率比较Fig.4 Comparison of the BER of different detection algorithms in 4×4MIMO 图5 8×8MIMO中各检测算法误比特率比较Fig.5 Comparison of the BER of different detection algorithms in 8×8MIMO 本文提出了一种基于信道矩阵条件数阈值的信号检测算法,首先将MIMO系统接收端信道矩阵的条件数计算出来,然后在给定的条件数阈值前提下,依据不同的条件数数值来选取相应的检测算法:在信道矩阵条件数低于阈值时,在接收端使用LLL-MMSE信号检测算法;而当信道矩阵条件数高于阈值时,在接收端采用基于排序分组的ML和LLL-MMSE联合的检测算法。仿真结果表明,本文算法通过预先设定条件数阈值从而使得算法在性能和复杂度之间获得了较好的平衡,最终达到了优化检测算法性能的目的。 图6 不同系统中选取LLL-MMSE算法的概率Fig.6 Probability of selecting LLL-MMSE algorithm in different systems [1] ZHANG Kangli, XIONG Chunlin, CHEN Bin, et al. A Maximum Likelihood Combining Algorithm for Spatial Multiplexing MIMO Amplify-and-Forward Relaying Systems[J]. IEEE Transactions on Vehicular Technology, 2015, 64(12):5767-5774. [2] YOU Weizhi, YI Lilin, HU Weisheng. A hybrid dynamic QRDM and ZF detection algorithm for MIMO-OFDM systems[C]// IEEE International Conference on Wireless Communications, Networking and Mobile Computing. Shanghai: IEEE, 2012: 1-4. [3] LI Xueru, EMIL Bjornson, LARSSON E G, et al. A Multi-Cell MMSE Detector for Massive MIMO Systems and New Large System Analysis[C]// Global Communications Conference (GLOBECOM). San Diego: IEEE, 2015:1-6. [4] JIANG Hua, SHEN Lizhen, WANG Tianjing. Improved lattice reduction-aided linear precoding in MIMO systems with limited feedback[J]. Electronics Letters, 2016, 52(13): 1183-1185. [5] WEN Qingsong, MA Xiaoli. Efficient Greedy LLL Algorithms for Lattice Decoding[J]. IEEE Transactions on Wireless Communications, 2016, 15(5): 3560-3572. [6] RADOSS L A, GUÉDON O, ALEXANDER E, et al. Condition number of a square matrix with i.i.d. columns drawn from a convex body[J]. Proceedings of the American Mathematical Society, 2012, 140(3): 987-998. [7] ROGER S, GONZALEZ A, ALMENAR V. Lattice-Reduction-Aided K-Best MIMO Detector based on the Channel Matrix Condition Number[C]//2010 4th International Symposium on Communications, Control and Signal Processing, ISCCSP. Limassol: IEEE, 2010:1-4. [8] NAJAFI H, DAMEN M O. Lattice-Reduction-Aided Conditional Detection for MIMO Systems[J]. IEEE Transactions on Communications, 2014, 62(11):3864-3873. [9] SONG Y, LIU C, LU F, et al. An improved detection algorithm based on Lattice reduction for MIMO system[C]// IEEE, International Symposium on Personal, Indoor, and Mobile Radio Communication. Washington: IEEE, 2014:285-289. [10] YONG S C, JAE K K, WON Y Y, et al. MIMO-OFDM Wireless Communications with MATLAB[M]. Singapore: John Wiley & Sons Pte Ltd, 2010:299-302. [11] EDELMAN A. Eigenvalues and Condition Numbers of Random Matrices[D]. Cambridge: Massachusetts Institute of Technology, 1989. The Foundation and Frontier Research Project of CQ CSTC(CSTC2015icyjA40040) LatticereductionaidedsignaldetectionalgorithmbasedonconditionnumberthresholdinMIMOsystems ZHOU Wei1,2, ZENG Xue1, FAN Peng2 1. Chongqing Key Laboratory of Mobile Communications Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R.China;2. College of Optoelectronic Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R.China) In multiple-input multiple-output(MIMO) systems,the ML detection algorithm has optimal performance but has high complexity, and the MMSE detection algorithm has lower complexity but its performance is poor. The higher condition number of channel matrix has bad effects on the detection performance of signals. Aimed at these problems, this paper provides a signal detection algorithm based on the condition number threshold of channel matrix, which can enhance the performance of traditional detection algorithm when the condition number is high. The algorithm selects the corresponding detection algorithm by comparing the condition number of channel matrix with the preset threshold: When the condition number is lower than the threshold, the algorithm chooses the LLL-MMSE algorithm which has lower complexity to reduce computational load; when the condition number is higher than the threshold, it chooses the sorted and grouped detection algorithm which combines ML and LLL-MMSE , ensuring the detection performance by increasing a certain amount of computational load. Through the simulation of the BER performance of the algorithm in different thresholds, results show that the proposed algorithm can outperform the traditional LLL-MMSE detection algorithm obviously. By presetting the threshold of the condition number, the algorithm can achieve a better balance between performance and complexity, and finally realize the optimizing of the performance of detection algorithm. multiple-input multiple-output; lattice reduction; condition number of matrix; threshold; lenstra-lenstra-lovasz 10.3979/j.issn.1673-825X.2017.06.001 2016-10-17 2017-10-27 曾 雪 zengxue 1992@126.com 重庆市基础与前沿研究计划项目(CSTC2015icyjA40040) TN929.5 A 1673-825X(2017)06-0711-06 周 围(1971 -),男,重庆合川人,教授,博士,硕士生导师,主要研究领域:无线移动通信技术、通信系统及信号处理、智能天线技术等。E-mail:zhouwei@cqupt.edu.cn。 曾 雪(1992 -),通信作者,女,重庆渝北人,硕士研究生,主要研究方向为无线移动通信技术以及信号检测技术。E-mail:zengxue1992@126.com。 樊 鹏(1991 -),男,四川遂宁人,硕士研究生,主要研究方向为无线移动通信技术以及信号检测技术。 (编辑:张 诚)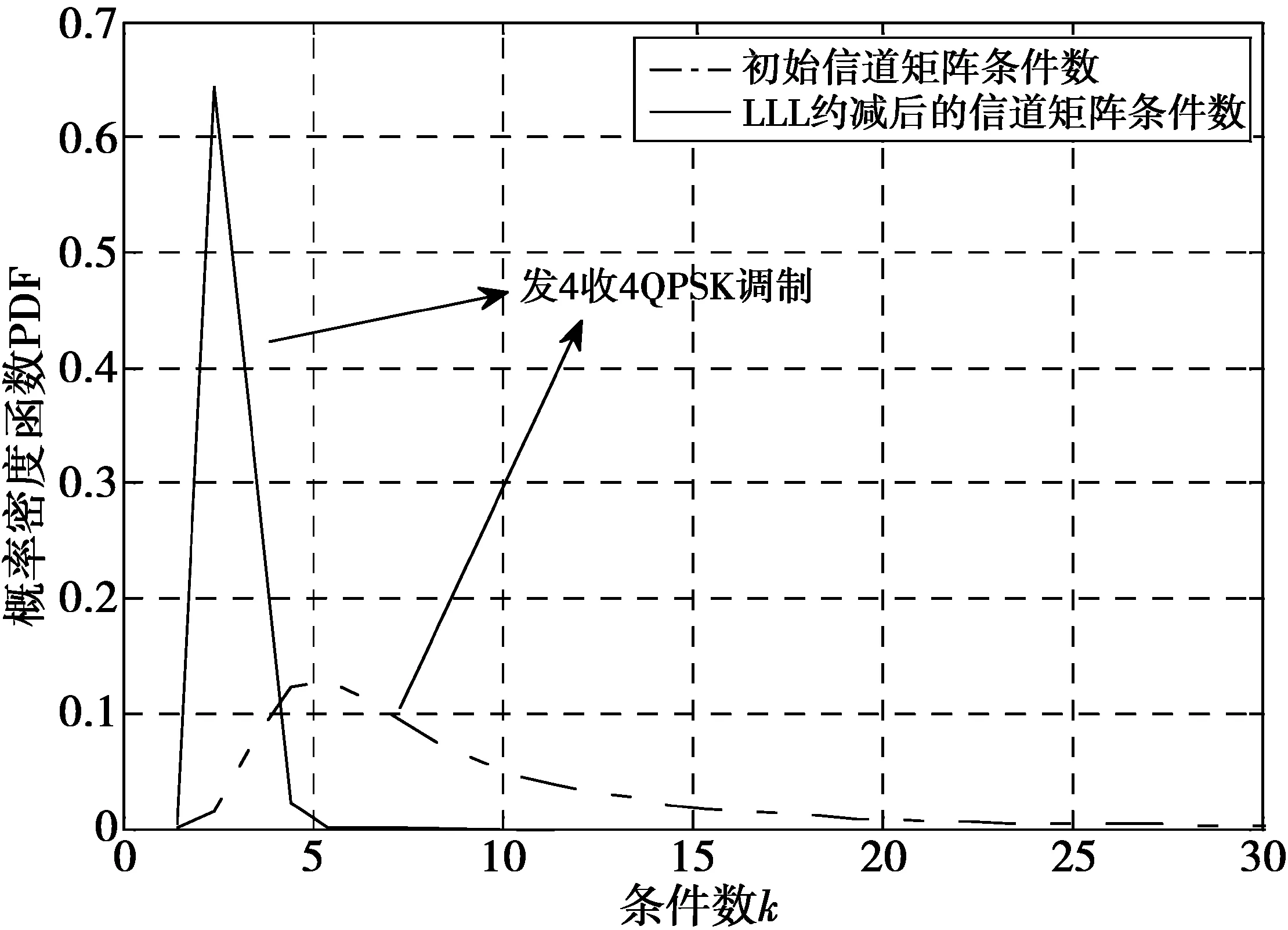
4 基于条件数阈值的改进算法
4.1 条件数阈值的选取
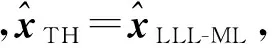

4.2 基于排序分组的ML和LLL-MMSE联合的检测算法
4.2.1 对子矩阵H1的选取
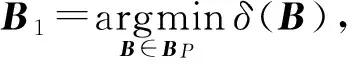
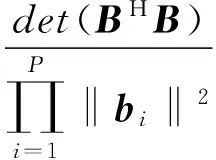
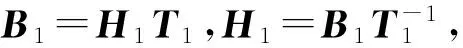
4.2.2 对子矩阵H2的选取
5 仿真结果及分析
6 总 结