复杂板件的隔声量仿真方法

赵蔷薇，贾尚帅，吴 宏，隋富生

（1.中车唐山机车车辆有限公司技术研究中心，河北 唐山 063035；2.声学研究所 中国科学院大学，北京 100190）

复杂板件的隔声量仿真方法

赵蔷薇1，贾尚帅1，吴 宏2，隋富生2

（1.中车唐山机车车辆有限公司技术研究中心，河北 唐山 063035；2.声学研究所 中国科学院大学，北京 100190）

针对波纹板、加筋板等复杂结构的隔声量仿真分析，提出一种分频段的仿真分析方法，获得复杂板件较为准确的隔声量仿真结果。在中频区域，采用考虑边界条件及阻尼损耗因子的有限元法对复杂板件进行仿真分析；而对一阶频率之前的低频区域，即刚度控制区域，采用等效法进行复杂板件的仿真分析；为了提高高频区域的计算效率，对其采用统计能量法计算隔声量。全频段的综合隔声量仿真结果与实验结果非常吻合，验证分频段仿真方法的有效性。

声学；复杂板件；分频段；有限元法；等效法；统计能量法

近年来，我国的高铁事业飞速发展，高铁的运行速度也日渐提升。随着高铁运行速度的增加，高铁的噪声问题变得尤为突出，车内噪声问题严重地影响了车内的舒适度，成为制约高铁运行速度的关键因素之一，对车体结构的优化设计是降低车内噪声问题的关键。

波纹板铝型材为高铁车体结构的主要组成部分；不锈钢加筋板为地铁车体结构的主要组成部分。因此对波纹板、加筋板等复杂板件的隔声特性展开研究十分重要。前人已经有一定的理论研究基础，辛锋先等通过空间谐波法与虚功原理获得了波纹板的隔声量结果，但理论结果与实验结果存在一定差异，并且没有考虑波纹板结构的边界条件[1–2]。

本文将介绍一种适用于波纹板、加筋板等复杂板件的隔声量仿真方法，通过在不同频段区域采用不同的仿真方法，来获取复杂板件的全频段隔声量仿真结果，得到的仿真结果与实验测试结果非常吻合，为复杂板件的隔声优化设计奠定基础。

首先对波纹板、加筋板等复杂板件进行实验测试，获得其隔声量实验数据及模态实验数据；然后对复杂板件采用不同的仿真方法，得到相应的隔声量仿真结果；最后对各方法的结果进行综合，获得复杂板件的全频段隔声量仿真结果。本文将以波纹板为例来进行仿真方法的详细介绍，并利用该方法进行加筋板的隔声量仿真分析，从而验证方法的可行性。

1 实验测试

首先对波纹板进行隔声量测试，波纹板的截面如图1所示。测得的波纹板隔声量结果如图2所示。

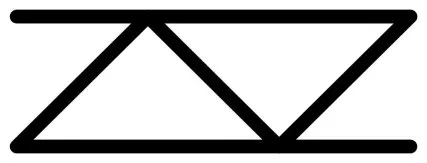
图1 波纹板铝型材的截面图

图2 波纹板的隔声量实验结果

同时，对波纹板进行模态测试，得到板件的模态频率等参数，波纹板的模态频率结果见表1。

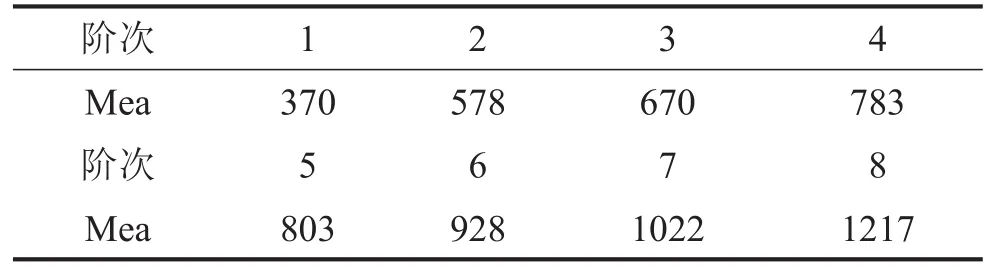
表1 波纹板的实验模态频率/Hz

2 有限元法

2.1 边界条件的确定

有限元法为仿真分析的经典方法，该方法基于CAE模型计算节点响应，考虑模态特性，得到的结果较为准确。

利用有限元法进行隔声量分析前，需确定波纹板的边界条件，将波纹板的CAE模型导入有限元软件中，分别施加固支边界(Clamped)与简支边界(Pinned)进行仿真计算[3]。得到波纹板固支边界下与简支边界下的模态仿真结果见表2。

表2 波纹板的仿真模态频率/Hz

通过对比模态频率的实验结果与仿真结果，可以看出，在进行波纹板隔声量仿真时，波纹板的边界条件可近似为固支边界条件。

2.2 CAE模型仿真

基于固支边界条件，利用有限元法对波纹板进行隔声量仿真分析，获得波纹板的隔声量仿真结果，并与实验结果进行对比，结果如图3所示。

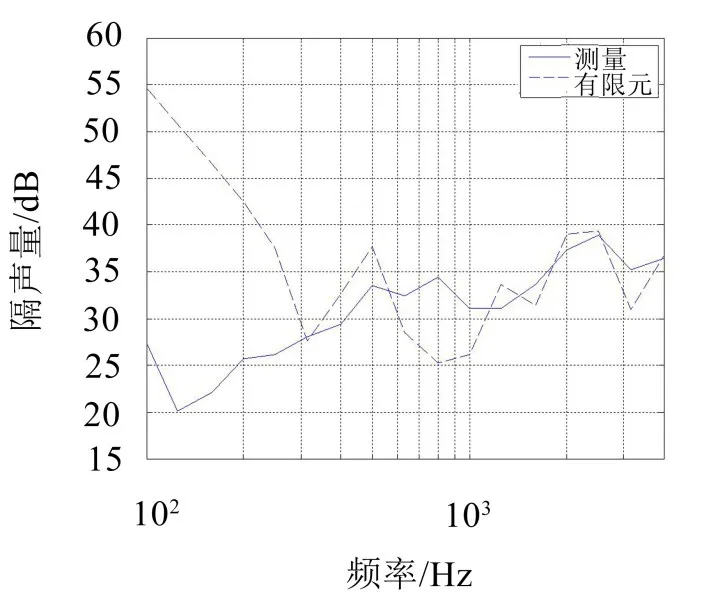
图3 基于有限元法和实验测试的波纹板隔声量结果对比图

从图3可以看出，有限元法获得的隔声量仿真结果与实验结果在两个区域有较大的差异，分别为630 Hz到1 250 Hz的中频区域以及315 Hz以下的低频区域。由于中频区域为质量控制区与阻尼控制区，因此未考虑到波纹板阻尼损耗因子的影响是导致该区域差异较大的原因。

2.3 阻尼修正

基于波纹板的模态测试数据，应用希尔伯特包络法求得波纹板1/3倍频程的阻尼损耗因子见表3。

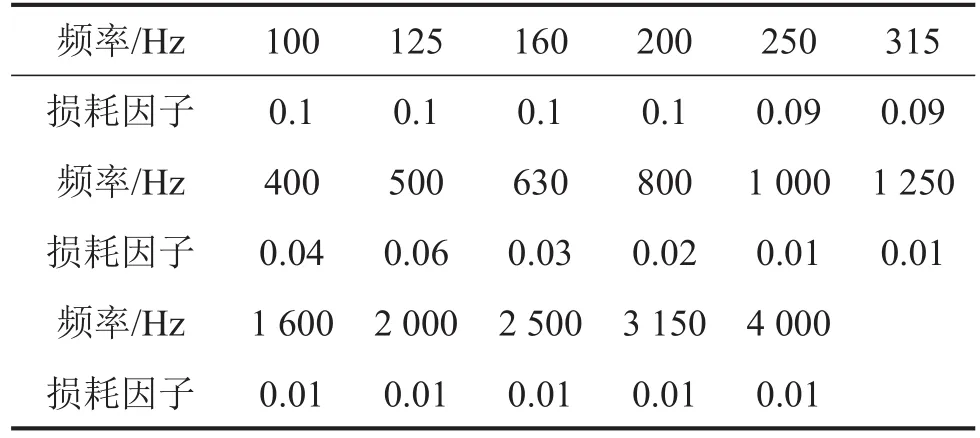
表3 波纹板的阻尼损耗因子

将阻尼损耗因子设置到有限元仿真模型中，重新对波纹板的隔声量进行仿真计算，得到阻尼修正后的波纹板隔声量仿真结果，与实验结果对比如图4所示。

从图4可以看出，阻尼修正后630 Hz到1 250 Hz的中频区域差异明显变小。这说明通过有限元法对复杂板件进行隔声量仿真时，不仅需要确定板件的边界条件，同时还需要考虑阻尼损耗因子的影响。

3 等效法

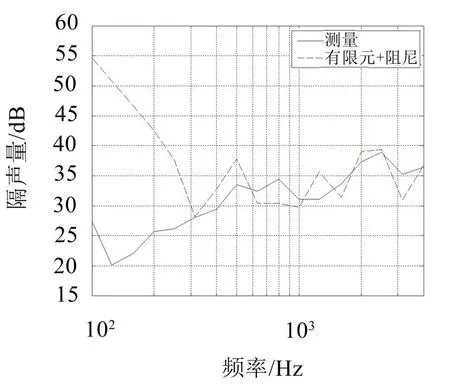
图4 阻尼修正后的隔声量结果对比图

从图4可以看出，考虑阻尼损耗因子后，315 Hz以下的低频区域的隔声量仿真结果与实验结果还是有很大的差异，这是由于波纹板的1阶频率为370 Hz，而有限元法是基于模态信息来求解板件隔声量的，因此利用有限元法在1阶频率以下的低频区域不能得到准确的仿真结果。

板件隔声量的低频区域为刚度控制区，因此采用力学等效的方式，利用等效法来对波纹板进行隔声量仿真分析，将波纹板等效为实心三明治板，表面板不变，中间层等效为各向异性介质，等效示意图如图5所示。

图5 铝型材结构等效示意图

波纹芯层等效为各向异性介质，主要是对模量、泊松比、密度进行等效。波纹芯层尺寸参量见图6。

图6 中间层波纹板几何参数

已有研究[4]表明等效参数可表示为以下形式。

弹性模量等效公式如下

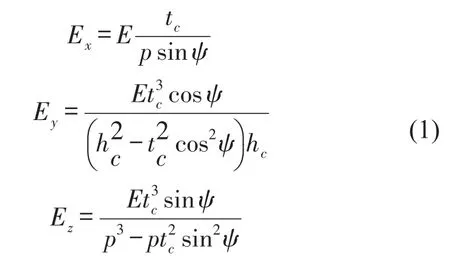
剪切模量等效公式如下

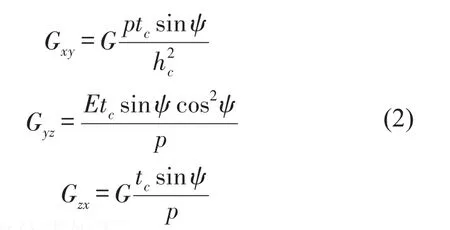
泊松比等效公式如下

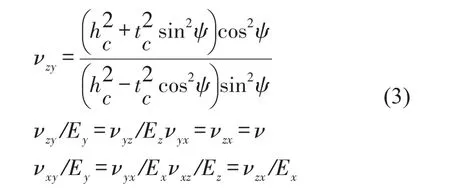
等效质量公式如下

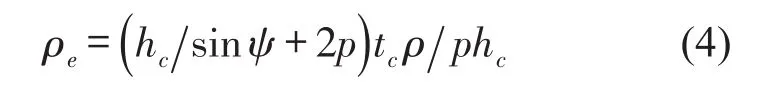
通过上述等效公式，计算中间层的各项参数。利用等效模型进行仿真分析，获得波纹板隔声量仿真结果，与实验结果对比如图7所示。

图7 基于等效法和实验测试的波纹板隔声量结果对比图

从图中可以看出，利用等效法获得的隔声量仿真结果在315 Hz以下的低频区域与实验结果基本吻合，随着频率的提高，等效法的仿真结果与实验结果差异变大。因此对于复杂板件，在一阶频率之前的低频区域可利用等效法进行仿真分析，可获取较为准确的隔声量仿真结果。

4 统计能量法

有限元法对板件中高频区域的隔声量仿真结果较为准确，但是随着计算频率的提高，网格质量的要求变高，导致计算的时间急剧增加。

统计能量法基于能量的角度计算，常用来计算高频响应，计算速度快，高频结果也较准确，因此为了提高板件仿真计算的效率，采用统计能量法来获取板件高频区域的隔声量仿真结果。

基于波纹板的CAE模型在仿真软件中建立SEA模型，对SEA模型进行仿真计算，获得波纹板的隔声量仿真结果，与实验结果对比如图8所示。

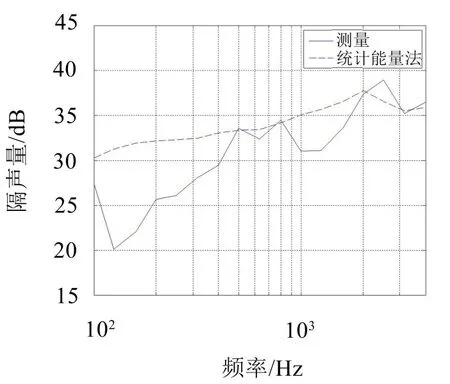
图8 基于统计能量法和实验测试的波纹板隔声量结果对比图

从图中可以看出，2 000 Hz以上的高频区域的隔声量仿真结果与实验结果基本一致，而随着计算频率的下降，仿真结果与实验结果差异变大。因此对于复杂板件，在2 000 Hz以上的高频区域可利用统计能量法来进行仿真分析，可以高效获取板件较为准确的隔声量仿真结果。

5 方法总结与验证

5.1 方法总结

结合上述三种仿真方法，在315 Hz之前的低频区域运用等效法进行仿真计算；在315 Hz到2 000 Hz的中频区域运用有限元法进行仿真计算；在2 000 Hz以上的高频区域运用统计能量法进行仿真计算，得到波纹板的综合仿真计算结果，并与实验结果进行对比，结果如图9所示。

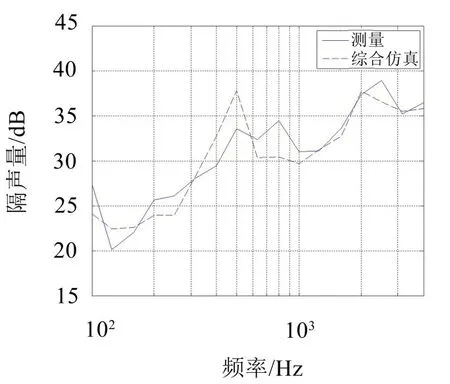
图9 波纹板综合的隔声量结果对比图

从图中可以看出根据综合的仿真分析方法得到的隔声量仿真结果与实验测试结果基本吻合，分频段的仿真方法获得了波纹板较为准确的全频段隔声量仿真结果。

5.2 方法验证

基于上述的分频段仿真方法，对地铁车体上的加筋板进行隔声量的仿真分析。得到地铁车体底架不锈钢板与侧墙钢板的隔声量仿真结果，并与实验结果对比，结果如图10、图11所示。

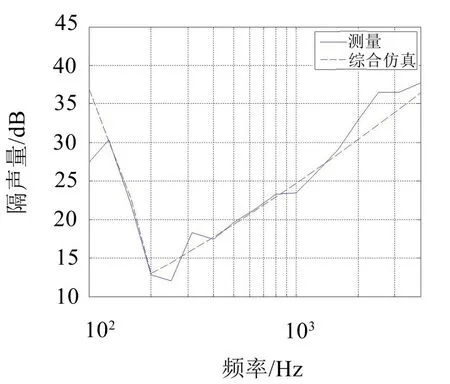
图10 底架不锈钢板综合的隔声量结果对比图

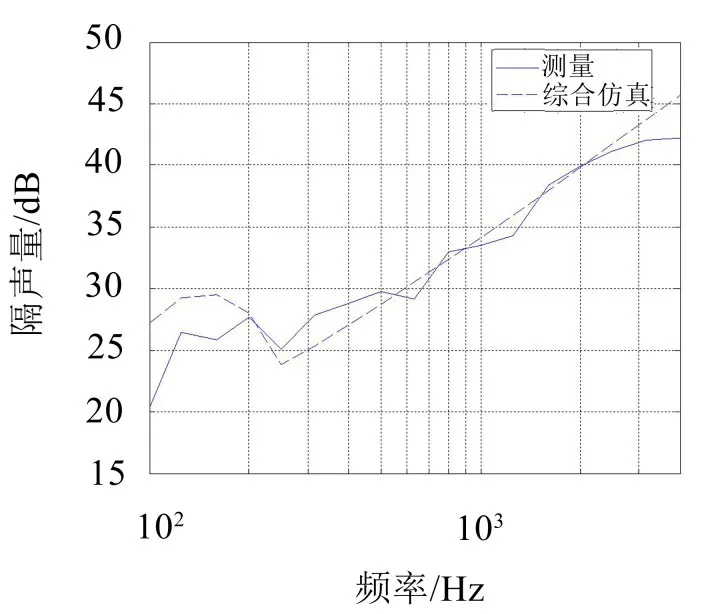
图11 侧墙钢板综合的隔声量结果对比图

从以上两张图可以看出，利用分频段的仿真方法得到地铁加筋板的隔声量仿真结果与实验结果非常一致，验证了分频段方法的有效性。

6 结语

本文对波纹板、加筋板等复杂板件进行了隔声量仿真分析，获得了板件较为准确的隔声量仿真结果。以波纹板为例，详细介绍了仿真方法的过程，在不同频段所采用的不同的仿真方法：在中频区域，采用考虑边界条件及阻尼损耗因子的有限元法；对一阶频率之前的低频区域，采用等效法；在高频区域，采用统计能量法，最终获得的波纹板隔声量仿真结果与实验结果非常吻合。同时将该方法应用到加筋板的隔声量仿真分析，同样获得了准确的仿真结果，验证了该方法的可行性，为复杂结构进一步的仿真优化奠定了基础。

[1]辛锋先，卢天健，陈常青.轻质金属三明治板的隔声性能研究[J].声学学报，2008，33(4)：340-347.

[2]SHEN C,ZIN F X,LU T J.Theoretical model for sound transmission through finite sandwich structureswith corrugated core[J].International Journal of Non-Linear Mechanics,2012,47(10):1066-1072.

[3]詹福良，徐俊伟.Virtual.Lab Acoustics声学仿真计算从入门到精通[M].西安：西北工业大学出版社，2013：22-24.

[4]王红霞，王德禹，李喆.三角形夹芯板夹心层的等效弹性常数[J].固体力学学报，28(2)：178-182.

[5]PANG YUET YAN,ORRENIUS ULF,STEGEMANN BERT,et al.Modelling sound transmission through floor structures in trains based on extruded profiles[C].Proceedings of the Vibro-Acoustic Users Conference,2004.

[6]张海澜.理论声学[M].北京：高等教育出版社，2012.

Simulation Method of Sound Insulation for Complex Panels

ZHAO Qiang-wei1,JIA Shang-shuai1,WU Hong2,SUI Fu-sheng2
(1.Product Technology Research Center,CRRC Tangshan CO.Ltd.,Tangshan 063035,Hebei China;2.Institute ofAcoustics,University of ChineseAcademy of Sciences,Beijing 100190,China)

A simulation analysis method based on frequency division is proposed.Simulation analysis of the sound insulation for complex panels is done by using this method.The accurate simulation results of sound simulation for the complex panels are obtained.In the intermediate frequency region,considering the boundary condition and loss factor,the FEM method is used for the simulation analysis.While in the low frequency region below the first-order natural frequency,which is the stiffness control region,the equivalent method is adopted for the simulation.To raise the computational efficiency in the high frequency region,the SEA method is applied.The simulation results of the overall sound insulation in the whole frequency range are all in good agreement with the experimental results,which verifies the validity of the frequency division method.

acoustics;complex panels;frequency division;finite element method;equivalent method;statistical energy method(SEA)

TH113.1

A

10.3969/j.issn.1006-1355.2017.06.018

1006-1355(2017)06-0090-04+125

2017-04-17

赵蔷薇（1985-），女，河北省廊坊市人，工学硕士，工程师，主要研究方向为轨道车辆振动噪声研究。

吴宏，男，博士生。E-mail:whdx1234@163.com