一种基于遗传算法的RSC码盲识别方法
2017-12-20张立民吴昭军钟兆根
张立民,吴昭军,钟兆根
1.海军航空大学 信息融合所,烟台 264001 2.海军航空大学 电子信息工程系,烟台 264001
一种基于遗传算法的RSC码盲识别方法
张立民1,吴昭军2,*,钟兆根2
1.海军航空大学 信息融合所,烟台 264001 2.海军航空大学 电子信息工程系,烟台 264001
针对目前递归系统卷积(RSC)码盲识别算法容错性差、计算量大的问题,提出了基于遗传算法的RSC多项式参数盲识别算法。首先根据RSC码特殊的编码结构,构建了基于遗传算法的识别模型,将结果向量的码重作为适应度函数,然后推导出了不同误码率条件下平均码重的理论值,实现了算法中最优门限的获得。该算法容错性能较好,并且最大计算量只与初始种群的规模、遗传代数的上限以及输出路数成正比。最后仿真验证表明,理论推导的码重分布情况能够与仿真结果较好地吻合,并且在误码率高达0.06的情况下,各种寄存器个数下的RSC码参数识别率接近于0.9。
RSC码;遗传算法;适应度函数;最优门限;盲识别
由于Turbo码在交织长度足够长且交织关系随机时,其容错性能能够逼近香侬限[1],所以被广泛运用于卫星通信、深空探测等领域[2],且成为3G、4G通信系统的信道编码标准之一。在Turbo码中,递归系统卷积(Recursive Systematic Convolutional,RSC)码是其主要的分量编码器,正确识别出RSC码的编码多项式,对于Turbo码交织器的识别具有重要意义[3-4]。
目前针对RSC码盲识别的传统算法主要有:解线性方程组方法、欧几里得算法、快速双合冲算法和Walsh-Hadamard变换等[5]。基于有限域中解线性方程组方法,利用码元之间线性约束关系来构建方程组[6],但当存在误码时,线性关系将遭到破坏导致识别失效,所以这种方法的容错性能较差。欧几里得算法[7]和快速双合冲算法[8]能够实现卷积码快速盲识别,但算法的容错性能不好。Walsh-Hadamard变换[9]在实现RSC码盲识别上具有极强的容错性能,但是算法的实质是一个穷举算法,计算量随着移位寄存器个数呈指数增加。Debessu等[10]首次提出了基于期望最大化(Expectation Maximization,EM)算法的RSC参数的盲识别方法,该方法在很低的信噪比下,编码参数的盲识别率能够达到很高,但在实际运用中,算法极易陷入局部极小值,导致算法识别错误。此外,还有许多算法基于软判决信息来识别,如文献[11],其容错性能较好但是计算量太大。目前RSC码盲识别算法存在计算量大、容错性能差等缺点,还需进一步对其进行深入研究。
基于此,本文充分利用遗传算法的迭代选优功能,对RSC码进行识别分析。该方法最大计算量仅与种群规模、遗传代数上限和码率有关,同时具有较好的容错性能。仿真结果表明:在误码率(Bit Error Rate, BER)达到10-2数量级时,各种寄存器个数下的RSC码参数的识别率能够达到0.9以上。
1 识别模型的建立
RCS码,其编码结构中,存在着反馈部分,能够有效避免各路低重量的码字与高重量的码字配对,常常作为Turbo码分量编码器,从而达到优良的纠错性能。图1所示为RSC码的编码结构[12]。

C1(D)=I(D)
(1)

(2)
其中:m为寄存器个数,设信息码元长度为L,则有
I(D)=I0+I1D+…+IL-1DL-1
(3)
(4)
(5)
将式(2)同乘以分母多项式,在二元域中相加,可以得到式(6),实际应用中I(D)可用式(1)替代。
C2(D)(g10+g11D+…+g1mDm)⊕
I(D)(g20+g21D+…+g2mDm)=0
(6)
式中:⊕表示二元域中的异或运算。利用式(6),将截获的码元在一个码元约束长度下,展开成卷积的形式,得到

图1 RSC码编码结构Fig.1 Encoding structure of RSC code

(7)
式中:ci,j为第2路码元构建的分析矩阵中的第i行、第j列元素;Ii,j为第1路信息码元构建的分析矩阵中的第i行、第j列元素;t=L/(m+1),符号·表示向下取整。当多项式参数识别正确时,无误码条件下,截获的信息码元应满足式(7),这是推导遗传算法适应度函数的核心。
本文假定RSC码的码率、码字起点已经完成了识别。文献[13]针对该问题进行了详细的说明,并提出了基于矩阵分析的识别算法,该算法具有较强的工程实用性。所以本文研究的重点在于仅仅依靠截获的码元序列识别出生成多项式的系数,从而最大概率地满足式(7)。本文提出了基于遗传算法的盲识别方法,该方法能够有效地识别出生成多项式的系数。
2 RSC码识别算法
2.1 算法原理
根据遗传算法的思想[14-15],在RSC码的识别过程中,将待识别的多项式参数{g10,g11,…,g1m,g20,g21,…,g2m}序列作为一个基因个体。首先随机生成一组种群,然后通过适应度函数进行筛选,选出优良个体再进行遗传,从而实现基因个体的寻优,而筛选出来的最优基因即待识别的多项式参数。由于多项式参数就是0、1序列,所以基因编码方式可以为其本身,避免了基因编码与解码的复杂性。
2.1.1 适应度函数选取
由式(7)可知,所得结果为t×1的列向量,正确的多项式参数能够使得该向量的码重为0;反之,列向量中1为随机分布,码重近似为t/2。当存在误码情况时,遗传过程中最佳基因个体一定能够使得列向量的码重最小,即以最大的概率满足整个方程组的成立。不妨设第i代中第j个个体基因序列为Si,j,含错方程结果t×1的列向量为bi,j,即
(8)

则可以得到
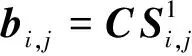
(9)
定义向量bi,j码重为向量中元素为1的个数,表示为weight(bi,j),则最优的个体的选择应满足:
(10)
从而得到适应度函数为f(i,j)=weight(bi,j)。
2.1.2 最佳门限的选择
分析式(9),当Si,j为正确多项式参数时,在含误码情况下,不妨设误码率为Pe,其编码约束关系不能够成立,取式(9)中一个编码方程为例,即
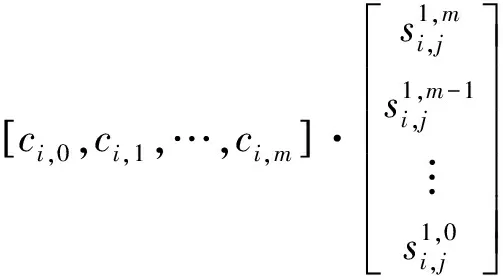
(11)
将式(11)进一步展开,得到

(12)
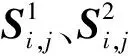
(13)

当Pe较小时,可以直接用k=1的情况近似代替。
求解出P后,weight(bi,j)服从均值为tP、方差为tP(1-P)的二项式分布,在该情况下,估计的多项式为实际的编码多项式。
当Si,j为不正确的多项式时,对应的向量bi,j相应位置行上元素为1的概率为1/2,故得到weight(bi,j)的分布列为
weight(bi,j)~
{B(tP,tP(1-P)) 当Si,j正确时
B(t/2,t/4) 当Si,j不正确时
(14)
当向量bi,j的行数t足够大时,weight(bi,j)近似服从正态分布,由此可进一步计算算法中的最优门限值。
不妨设Si,j为不正确多项式的事件为H1,Si,j为正确的事件为H0,D0为事件H0的观测空间,D1为事件H1的观测空间,设定虚警概率P(D0|H1)为0.001,最优门限为Λ。则
(15)
(16)
2.2 算法具体步骤
基于遗传算法的思想,将生成多项式系数作为个体基因来设置种群。在已经确定出适应度函数以及最优门限的条件下,可以得到RSC码盲识别算法的基本过程为:首先,随机确定出一定规模的种群,种群个体基因为RSC码生成多项式的系数;然后,通过个体之间随机的交叉配对繁殖以及基因突变产生子代;最后,通过适应度函数进行筛选,确定优良个体,继续进行遗传繁衍,直到适应度函数值大于门限值或是遗传的代数超出设置的遗传代数上限时,算法识别过程结束。具体步骤为:
步骤1以多项式的系数0、1序列作为基因的编码方式,随机产生一个规模数量为M的种群。
步骤2将产生的种群个体最大程度地进行两两随机配对交叉繁衍,以概率Pc将种群个体进行变异,从而产生出新的子代,并将新的子代与父代相结合,形成更大规模的种群。
步骤3将截获的码元按码率分成2路,并将每路码元按顺序按行排列成t×(m+1)的矩阵I、C,按照式(9)计算种群每个个体的适应度函数值。
步骤4将适应度函数值按从小到大的顺序进行排列,选取前M个个体,作为新一个种群,重复步骤1,直到某一代的最小适应度函数值小于最佳门限Λ或是遗传代数大于设定的遗传代数G,识别算法结束,输出最佳基因个体,即识别的多项式参数。
参数识别算法的具体流程图如图2所示。
整个算法虽然是在码率为1/2时推导出来的,但是同样适用于码率为1/n的情况。识别方法为:首先按照码率为1/2的方式,识别出反馈多项式与第1个前项多项式参数,然后利用识别出来的反馈多项式参数,同样按照码率为1/2的算法依次识别出第2个,第3个,直到第n-1个前向多项式参数,从而完成1/n的RSC码盲识别。
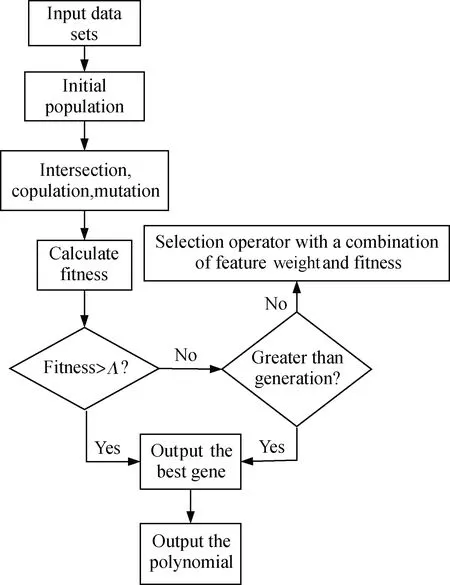
图2 参数识别算法流程图Fig.2 Flow chart of algorithm for parameters recognition
2.3 计算复杂度分析
假定算法初始种群规模数为M,遗传代数上限为G,RSC码码元寄存器个数为m,输出码元路数为n,设截获的码元序列所构成的数据矩阵C、I均为t×(m+1)大小的矩阵。按照文献[5]对运算量的定义,有限域中加法与乘法定义为1次运算,实数域中加法为1次运算,乘法为4次运算。按照2.2节中的识别步骤,可得到本文算法的计算复杂度complex为
complex=2n(m+1)tMG
(17)
从计算复杂度的表达式来看,算法的复杂度主要来源于种群规模数量以及设定的最大遗传代数,二者都是可以人为控制的。当寄存器个数较小时,可以减少M与G来实现计算量的减小。
3 仿真验证
3.1 不同误码下,结果向量码重分布
在最优门限的推导过程中,对结果向量bi,j的码重分布作了理论的推导,不同误码率条件下,将仿真结果与推导的理论结果作比较。为了反映出统计特性,仿真时设定截获的码元为10 000个。在编码多项式正确时,选取(7,5)、(13,17)、(25,37)、(45,67)代表了4种寄存器个数的多项式,在不同误码率下,将bi,j平均码重的理论值与仿真值对比;当编码多项式不正确时,选择(27,13)多项式为不正确多项式,而(25,37)为正确多项式,同样将bi,j的平均码重理论值与仿真值对比,误码率设定为0~0.5,间隔取值为0.01,得到的结果向量码重随误码率变化的理论与仿真结果如图3所示。
从仿真结果与理论值对比来看,可得出结论:当多项式参数正确时,理论值与仿真值相一致,二者相当接近;当多项式不正确时,结果向量bi,j的码重理论值为1 000,而仿真结果正好在1 000附近来回波动,说明理论推导结果正确。综上所述,2.1.2节中的码重分布理论推导结果能够反映实际的情况。

图3 仿真结果与理论结果对比Fig.3 Comparison of simulation and theoretic results
3.2 寄存器个数对进化速度的影响
由于寄存器个数越多,生成多项式系数就越大,反映在种群个体的基因序列上就越复杂。设定初始种群数目为每种编码器所有可能个体总数的2/3(如寄存器个数为3的情况,所有可能的个体总数为23×2,初始种群数目可设定为42),分别在寄存器个数为2、3、4、5下,研究优良个体进化的速度,设定误码率为0.01,得到在不同寄存器个数下,优良基因进化速度结果如图4所示。
从仿真的结果来看,寄存器个数对于进化速度影响较为明显,当编码器中寄存器的个数等于2时,优良个体的占有率在第5代就达到了峰值;而寄存器个数为5时,遗传代数则需要大于25代才能达到峰值。说明寄存器个数越多,优质基因越难寻得。从曲线变化趋势上来看,一旦出现优质个体基因,那么种群个体急剧向优质个体进化。故对于寄存器个数较多的编码多项式估计,可以选择采用增加初始种群规模,增加进化代数上限来克服,但是同时也增加了识别的时间。

图4 不同寄存器个数下的优良基因进化速度Fig.4 Evolution speed of excellent genetic with different number of registers
3.3 算法的容错性分析
3.3.1 寄存器个数对算法的影响
仿真选取的RSC码编码形式主要有:RSC(2,1,2)、RSC(2,1,3)、RSC(2,1,4)、RSC(2,1,5) 4种;寄存器个数分别为:2、3、4、5;多项式的形式为(7,5)、(13,17)、(25,37)、(45,67);多项式的表示方式为八进制。设定截获的码元数目为1 000个, 设定初始种群数目与3.2节的方法一致,配对方式为最大程度的两两随机配对交叉,变异概率为0.05。为提高算法的实时性,设定遗传代数上限为20代,误码率为0~0.2,间隔取值为0.01,采用蒙特卡罗仿真,统计在不同误码率条件下,参数正确识别率结果如图5所示。
从识别结果上看,算法的容错性能较强,在寄存器个数较少时,尤为明显。但是当寄存器个数增加时,算法的容错性下降,主要原因为寄存器个数越多,误码出现在寄存器个数内的概率就越大,造成结果向量的对应行位置不为0,以至码重增加导致误判。
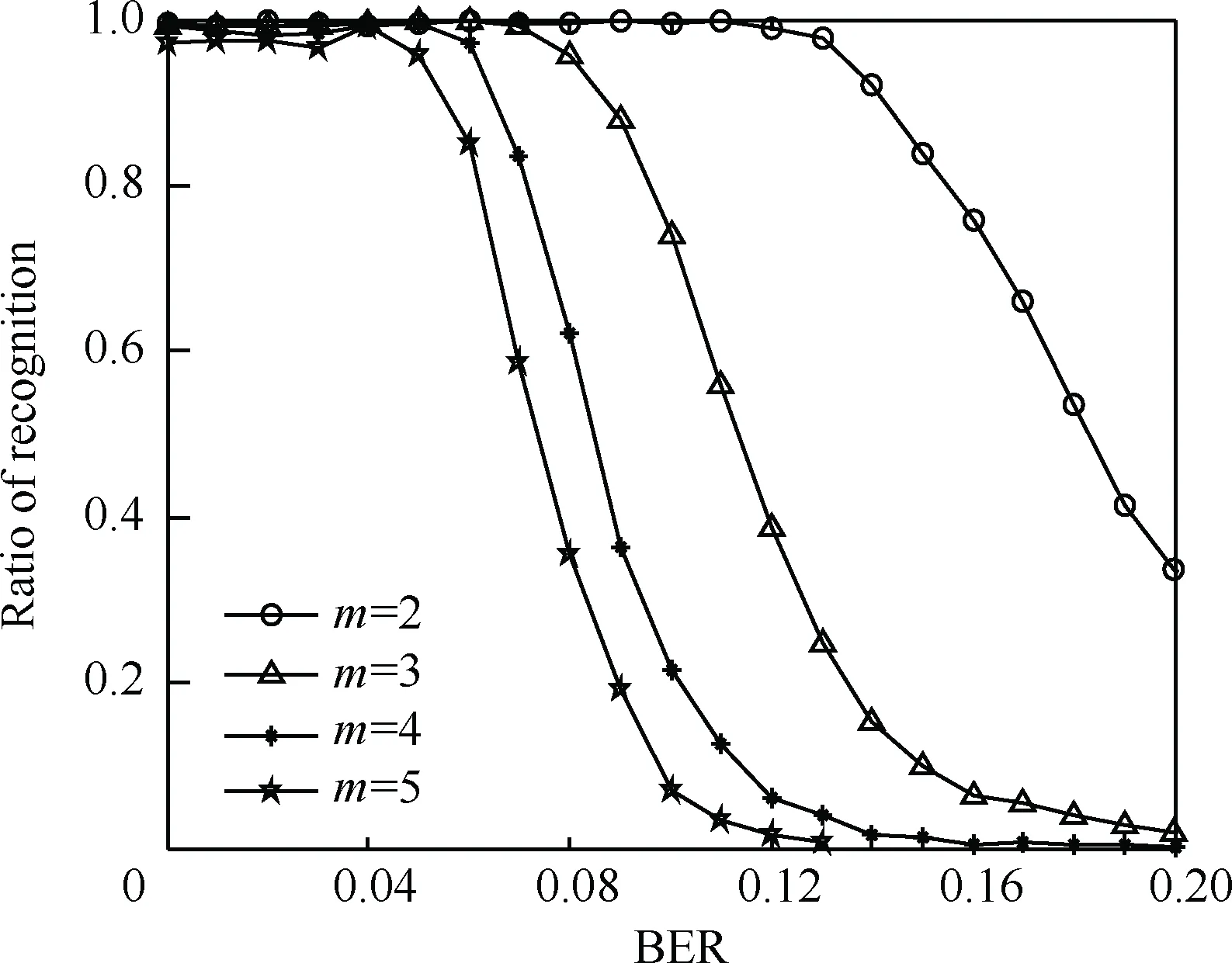
图5 寄存器个数对算法性能的影响Fig.5 Performance of algorithm with different number of registers
3.3.2 估计的寄存器个数对算法的影响


图6 估计的寄存器个数对算法的影响Fig.6 Performance of algorithm with different estimated number of registers
从图6中可以看出,算法的性能随着寄存器个数增加而下降,但是与图5相比,其下降的幅度并不大,4条曲线相对比较接近。分析其主要原因为:虽然估计的寄存器个数增加了,但是却导致多维度空间中多解的出现,使得遗传算法更容易找到正确解。
3.3.3 截获码元长度对算法的影响
仿真选取的RSC码生成多项式为(13,17),其寄存器个数为3,设定截获的码元长度L为500、1 000、1 500、2 000,误码率的变化范围为0~0.15,间隔取值为0.01,蒙特卡罗仿真次数为1 000次,统计在不同误码率下多项式的正确识别率,实验结果如图7所示。
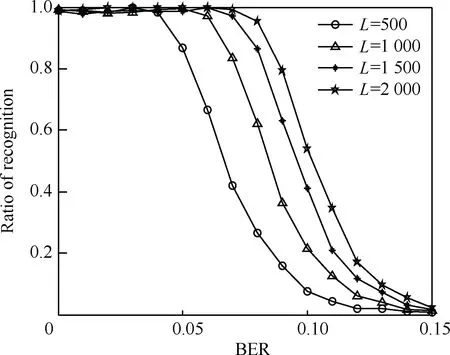
图7 截获码元长度对算法性能的影响Fig.7 Performance of algorithm with different lengths of intercepted code
从仿真结果来看,截获码元长度对于算法的影响较为明显,随着截获码元的增加算法的容错性能得到了提高,但是计算的复杂度也增加了。同时从图7中还能得到,随着截获码元的进一步增大,识别性能曲线逐步接近,提高不大。
3.3.4 种群规模与遗传代数对算法的影响
同样选取(13,17)为实际编码多项式,设定截获的码元长度为1 000,在固定的最大遗传代数为20的情况下,种群规模为50、100、170;同时,在固定的种群规模为170时,最大遗传代数为1、3、5、20;误码率变化范围为0~0.2,间隔取值为0.01,蒙特卡罗试验次数为1 000,得到如图8所示的结果。

图8 种群规模与遗传代数对算法的影响Fig.8 Performance of algorithm with different populations and genetic generations
从得到的实验结果来看,种群规模对于算法的识别性能影响较大,在低误码率的条件下,当种群规模较小时,识别率曲线会出现震荡现象,随着误码率的增加,种群规模的影响渐渐消失;最大遗传代数的影响不是特别明显,除了遗传代数为1的情况,不管是在低误码率还是在高误码率的情况下,其识别性能差距不大,如代数为3、5、20的性能曲线没有太大区别。由此可知,在实际应用该算法时,可以根据实际的信道情况来选择种群规模以及最大遗传代数,如在低误码率条件下,可选择较大的种群规模和较小的遗传代数;在高误码率条件下,选择较小的种群规模和较小的遗传代数,从而实现计算量的减少,提高算法的实时性。
3.4 与其他算法的比较
首先与本文算法作比较的是经典的Walsh-Hadamard变换,仿真中选取的多项式与3.3.1节中一致,误码率变化范围为0~0.2,间隔取值为0.01,蒙特卡罗试验次数为1 000,得到本文算法与Walsh-Hadamard变换性能比较结果如图9所示,实线为本文算法,虚线为Walsh-Hadamard变换。
从仿真结果上来看,在寄存器个数较少时,本文算法要远远好于Walsh-Hadamard变换;而当寄存器个数增多时,本文算法的性能渐渐劣于Walsh-Hadamard变换。究其主要原因为:Walsh-Hadamard变换实质是一种穷举算法,能够将所有解的情况考虑进去;而遗传算法主要是通过基因交叉、变异来寻优,实现参数的估计,不可避免地使有些情况下正确的解漏掉,导致参数识别失败。
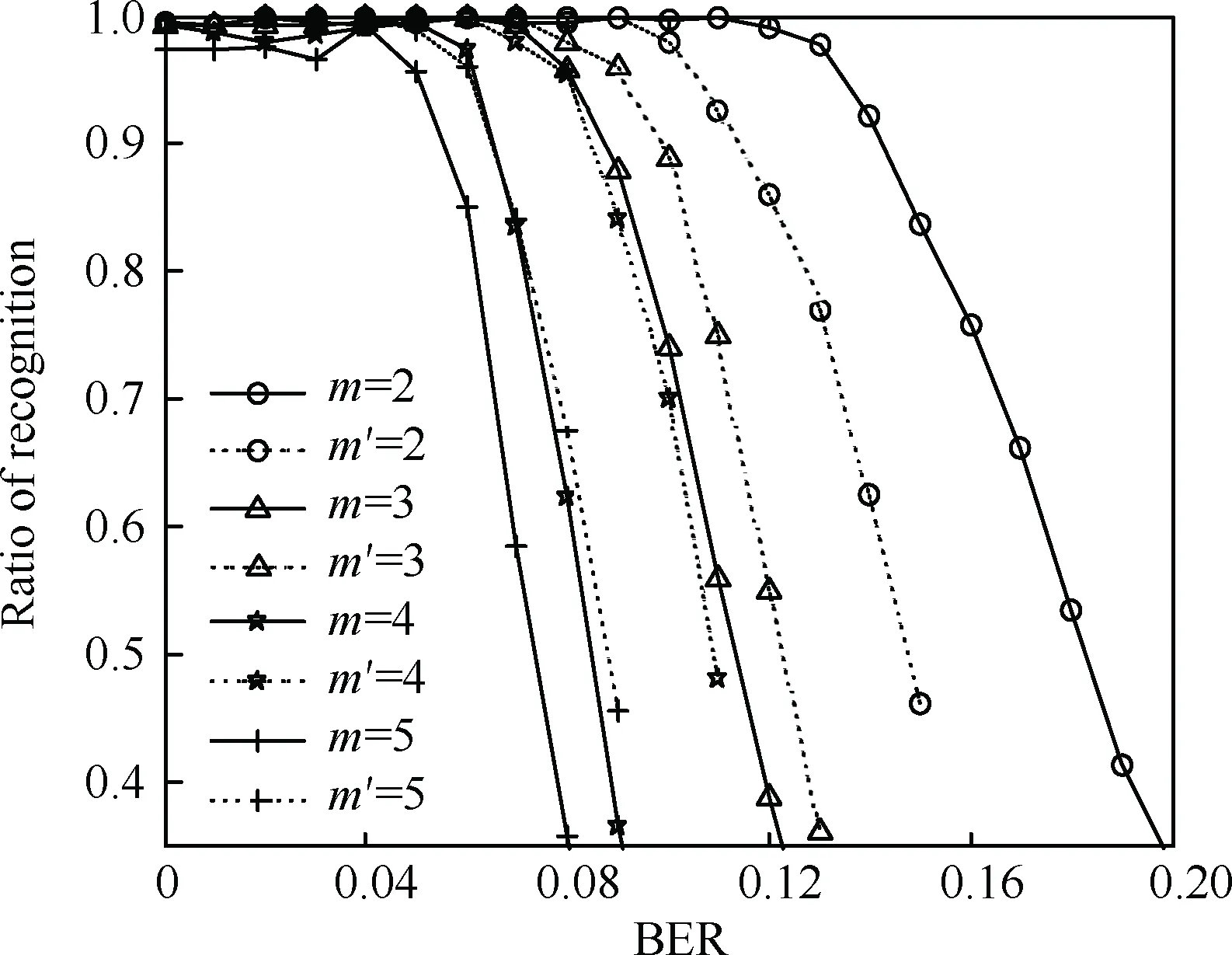
图9 本文算法与经典算法性能比较Fig.9 Comparison between presented algorithm and classical algorithm
其次与本文算法进行比较的是目前较为新颖的识别算法,即基于信道软判决信息识别算法[11]和快速Walsh-Hadamard变换(FWHT)算法[16]。选取识别生成多项式为(7,5),其寄存器个数为2,默认调制方式为2 PSK,进一步得到3种识别算法的性能对比曲线如图10所示。
从识别性能上来看,本文提出的算法要好于软判决算法和FWHT算法。软判决算法和FWHT算法在误码率0.09左右,才能达到0.9以上的识别率。而本文算法在误码率高达0.14时,就能够达到0.9以上。
从计算复杂度上主要与经典算法、软判决算法和FWHT算法3种算法对比。选取寄存器个数为2~6,总共5种RSC码编码器,将这4种算法在同一条件下,对参数进行识别,得到完成一次识别所需要的时间。其中遗传算法是识别100次后取平均时间,识别消耗时间见表1所示。
从表1来看,提出的基于遗传算法下的RSC码识别方法时效性要远好于经典算法与基于软判决算法,特别是当寄存器个数增加时,识别时间的差距越来越明显,其时效性略差于FWHT算法。
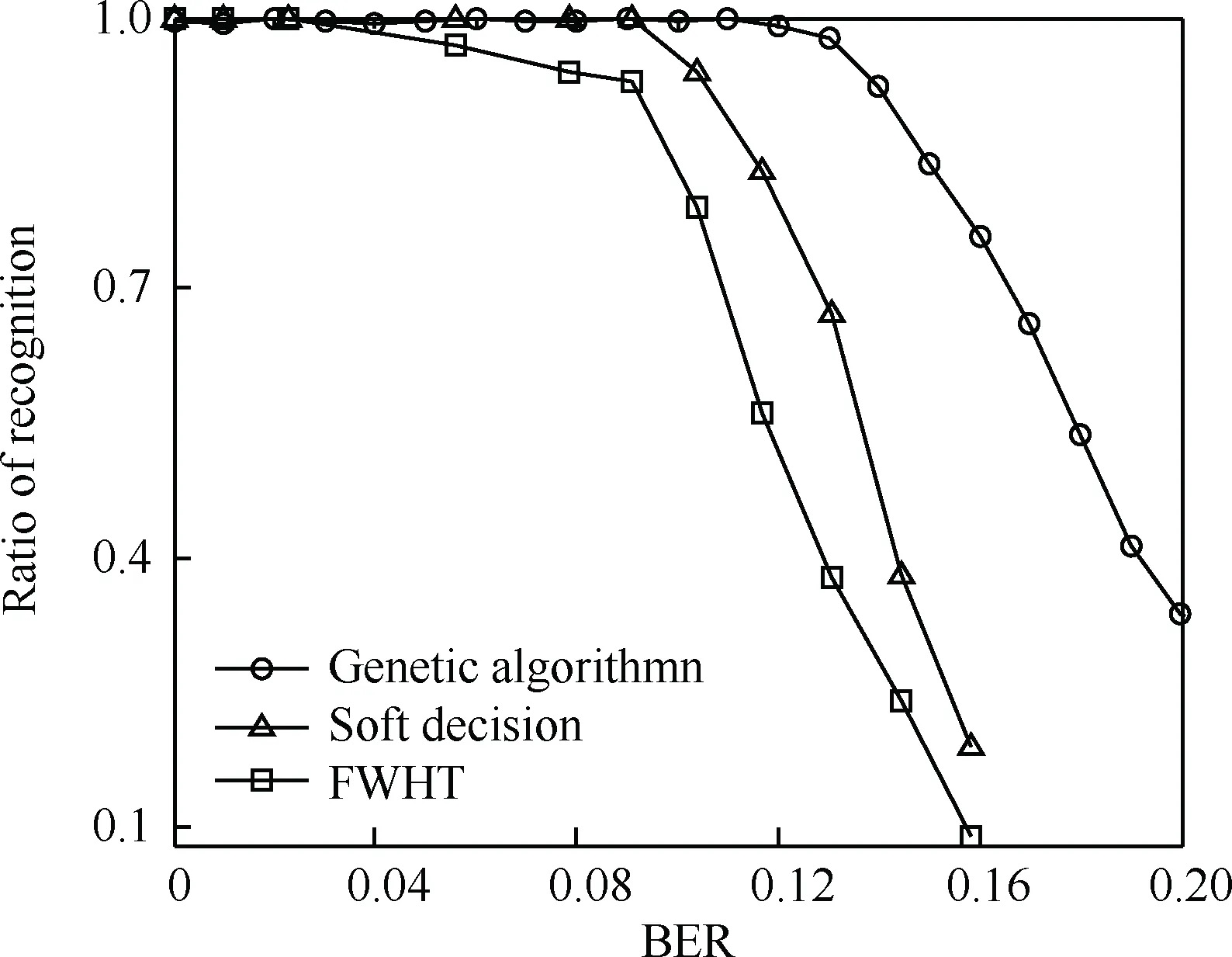
图10 3种算法的比较Fig.10 Comparison of three algorithms
表1 遗传算法与其他算法识别时间对比
Table 1 Comparison of time-consumption betweengenetic algorithm and others
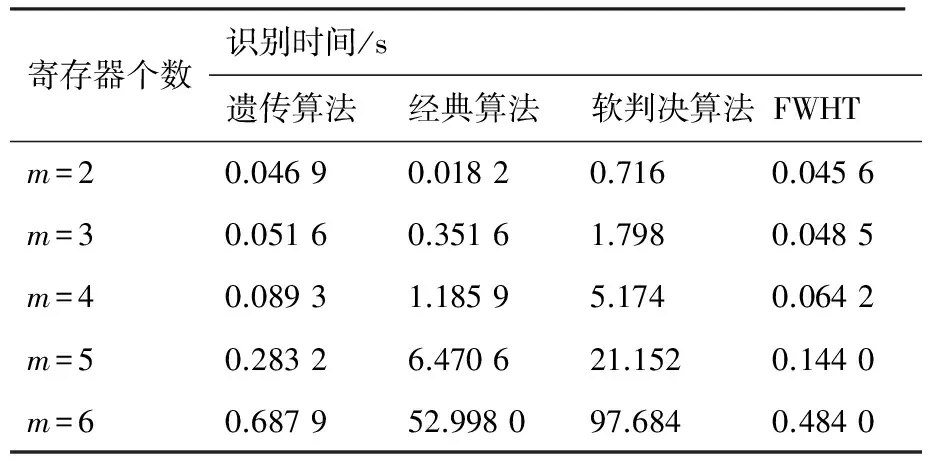
寄存器个数识别时间/s遗传算法经典算法软判决算法FWHTm=20.04690.01820.7160.0456m=30.05160.35161.7980.0485m=40.08931.18595.1740.0642m=50.28326.470621.1520.1440m=60.687952.998097.6840.4840
主要原因是:Walsh-Hadamard变换和基于软判决算法是一个穷尽算法计算量与寄存器个数呈指数倍增加,不可避免要耗费大量的时间;而FWHT算法是经典算法的改进,采用了蝶形变换方式,运算量相比于经典算法大大减少,故其识别时间略好于本文算法。同时还需要注意到基于软判决的识别算法虽然识别性能较好,但识别时间要远大于经典算法。主要原因为识别过程中参与运算的是软判决信息,不同于二元域中的0、1序列,计算方式更加复杂。
综合识别率和时效性两大因素,本文算法要优于其他3种算法。
4 结 论
1) 构建出了RSC码识别数学模型,提出了基于遗传算法的RSC码编码多项式盲识别方法,推导了适应度函数和最优门限值。
2) 通过仿真分析了寄存器个数对进化速度的影响,分2种情况,对结果向量码重分布的仿真结果与理论结果进行了对比,结果表明寄存器个数越少,进化速度越快,同时理论推导的向量码重分布与仿真结果非常吻合,说明理论推导码重概率分布是正确的。
3) 研究了算法的容错性能,讨论寄存器个数、截获码元长度、初始种群数目和最大进化代等因素对算法容错性能的影响。从容错性能曲线上看,提出的算法容错性能较好,在误码高达0.06的情况下,参数的识别率在0.9以上。
4) 将本文算法与经典算法、软判决算法和FWHT算法从容错性能和识别时效性方面进行了对比。从结果上来看,本文算法容错性明显好于软判决算法和FWHT算法,并且时效性远好于经典算法和软判决算法。综合计算复杂度和识别性能两个方面的因素,本文算法性能更加优越。
[1] MUKHTAR H, AL-DWEIK A, SHAMI A. Turbo product codes: Applications, challenges, and future directions[J]. IEEE Communications Surveys & Tutorials, 2016, 18(4): 3052-3069.
[2] LI H, GAO Z, ZHAO M, et al. Partial iterative decode of turbo codes for on-board processing satellite platform[J]. IEEE Journals & Magazines, 2015, 12(11): 1-8.
[3] 任亚博, 张健, 刘以农. 高误码率下Turbo码交织器的恢复方法[J]. 电子与信息学报, 2015, 37(8): 1927-1930.
REN Y B, ZHANG J, LIU Y N. Reconstruction of turbo-code interleaver at high bit error rate[J]. Journal of Electronics& Information Technology, 2015, 37(8): 1927-1930 (in Chinese).
[4] 刘俊, 李静, 彭华. 基于校验方程平均符合度的Turbo码交织器估计[J]. 电子学报, 2016, 44(5): 1213-1217.
LIU J, LI J, PENG H. Estimation of turbo-code interleaver based on average conformity of parity-check equation[J]. Acta Electronica Sinica, 2016, 44(5): 1213-1217 (in Chinese).
[5] 谢辉, 黄知涛, 王峰华. 信道编码盲识别技术研究进展[J]. 电子学报, 2013, 41(6): 1166-1176.
XIE H, HUANG Z T, WANG F H. Research progress of blind recognition of channel coding[J]. Acta Electronica Sinica, 2013, 41(6): 1166-1176 (in Chinese).
[6] BARBIER J. Reconstruction of turbo-code encoders[J]. The International Society for Optical Engineering, 2005, 5819: 463-473.
[7] 解辉, 王峰华, 黄知涛, 等. 基于改进欧几里得算法的卷积码快速盲识别算法[J]. 国防科技大学报, 2012, 34(6): 159-162.
XIE H, WANG F H, HUANG Z T, et al. A fast method for blind recognition of convolutional codes based on improved Euclidean algorithm[J]. Journal of National University of Defense Technology, 2012, 34(6): 159-162 (in Chinese).
[8] 邹艳, 陆佩忠. 关键方程的新推广[J]. 计算机学报, 2006, 29(5): 711-718.
ZOU Y, LU P Z. A new generalization of key equation[J]. Chinese Journal of Computers, 2006, 29(5): 711-718 (in Chinese).
[9] 刘健, 王晓军, 周希元. 基于Walsh-Hadamard变换的卷积码盲识别[J]. 电子与信息学报, 2010, 32(4): 884-888.
LIU J, WANG X J, ZHOU X Y. Blind recognition of convolutional coding based on walsh hadamard transform[J]. Journal of Electronics & Information Technology, 2010, 32(4): 884-888 (in Chinese).
[10] DEBESSU Y G, WU H C, JIANG H. Novel blind encoder parameter estimation for turbo codes[J]. IEEE Communications Letters, 2012, 16(16): 1917-1920.
[11] 于沛东, 李静, 彭华. 一种利用软判决的信道编码识别新算法[J]. 电子学报, 2013, 41(2): 302-305.
YU P D, LI J, PENG H. A novel algorithm for channel coding recognition using soft decision[J]. Acta Electronica Sinica, 2013, 41(2): 302-305 (in Chinese).
[12] 武恒洲, 罗霄斌, 刘杰. Turbo码盲识别技术研究[J].无线电工程, 2015, 45(5): 24-27.
WU H Z, LUO X B, LIU J. Research on blind recognition of turbo codes[J]. Journal of Radio Engineering, 2015, 45(5): 24-27 (in Chinese).
[13] 张旻, 陆凯, 李歆昊, 等.归零Turbo码的盲识别方法[J]. 系统工程与电子技术, 2016, 38(6): 1424-1427。
ZHANG M, LU K, LI X H, et al. Blind recognition method for the turbo codes on trellis termination[J]. Journal of Systems Engineering and Electronics, 2016, 38(6): 1424-1427 (in Chinese).
[14] QIU M, ZHONG M, LI J, et al. Phase-change memory optimization for green cloud with genetic algrithm[J]. IEEE Transactions on Computers, 2015, 64(12): 3528-3540.
[15] 杨振强, 王常虹, 庄显义. 自适应复制、交叉和突变的遗传算法[J]. 电子与信息学报, 2000, 22(1): 112-117.
YANG Z Q, WANG C H, ZHUANG X Y. The adaptive genetic algorithms of copy, intersect and mutation[J]. Journal of Electronics & Information Technology, 2000, 22(1): 112-117 (in Chinese).
[16] 林晓娴, 王维欢. SIMD-BF模型上的并行FWHT算法研究[J]. 计算机时代, 2011(1): 30-32.
LIN X X, WANG W H. A study of parallel FWHT algorithm based on SIMD-BF model[J]. Computer Era, 2011(1): 30-32 (in Chinese).
BlindidentificationofRSCcodebasedongeneticalgorithm
ZHANGLimin1,WUZhaojun2,*,ZHONGZhaogen2
1.InstituteofInformationFusion,NavalAeronauticalUniversity,Yantai264001,China2.DepartmentofElectronicandInformationEngineering,NavalAeronauticalUniversity,Yantai264001,China
ToaddresstheproblemsofpoorperformanceandheavycomputationinblindidentificationofRecursiveSystematicConvolutional(RSC)code,anewalgorithmforblindidentificationofRSCpolynomialparametersisproposedbasedonthegeneticalgorithm.ConsideringthespecialstructureofRSCcode,theidentificationmodelisconstructedbasedonthegeneticalgorithm.Theweightoftheresultvectorisusedasfitnessfunction,andthetheoreticalvalueoftheaveragecodeweightisderivedatdifferentBitErrorRates,astheresults.Theoptimalthresholdisthenobtained.Theperformanceoftheproposedalgorithmisgood,andthemaximumamountofcalculationisonlyproportionaltotheinitialpopulationsize,geneticgenerations,andpathsofoutputs.Thesimulationresultsshowthatthetheoreticalderivationofthecodeweightisingoodagreementwiththesimulationresults,andtherecognitionrateoftheRSCcodeiscloseto0.9atdifferentnumberofregisterswhentheBitErrorRateisupto0.06.
RecursiveSystematicConvolutional(RSC)code;geneticalgorithm;fitnessfunction;optimalthreshold;blindidentification
2017-03-15;Revised2017-06-27;Accepted2017-07-04;Publishedonline2017-07-071148
URL:http//hkxb.buaa.edu.cn/CN/html/20171126.html
.E-mailwuzhaojun1992@qq.com
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2017.321246
V243.1; TN911.7
A
1000-6893(2017)11-321246-10
2017-03-15;退修日期2017-06-27;录用日期2017-07-04;< class="emphasis_bold">网络出版时间
时间:2017-07-071148
http://hkxb.buaa.edu.cn/CN/html/20171126.html
.E-mailwuzhaojun1992@qq.com
张立民,吴昭军,钟兆根.一种基于遗传算法的RSC码盲识别方法J. 航空学报,2017,38(11):321246.ZHANGLM,WUZJ,ZHONGZG.BlindidentificationofRSCcodebasedongeneticalgorithmJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):321246.
(责任编辑:苏磊)
