基于模糊C-均值聚类医学图像分割的优化算法
2017-12-20廖林峰邱晓晖
廖林峰,邱晓晖
(南京邮电大学 通信与信息工程学院,江苏 南京 210003)
基于模糊C-均值聚类医学图像分割的优化算法
廖林峰,邱晓晖
(南京邮电大学 通信与信息工程学院,江苏 南京 210003)
模糊C-均值聚类(FCM)算法在分割模糊的医学图像中有很好的效果,通过设置初始聚类中心,根据每个像素的隶属度来划分属于哪一类,采用迭代的方式来得到分割结果。针对FCM算法容易受到聚类中心初始值和噪声的影响,采用遗传算法和粒子群算法的结合算法来确定一组合适的初始聚类中心,通过遗传算法和粒子群算法的结合算法加快了单纯使用遗传算法确定初始聚类中心的收敛速度;再通过引入像素的邻域信息,重构标准FCM算法中的目标函数,以提高邻域像素和中心像素之间的相似程度,使得相邻的像素更容易划分到同一类别,克服了标准FCM算法只考虑像素间的灰度值而导致对噪声和异常值的敏感问题。将该方法应用到核磁共振成像(MRI)脑部图像分割实验中,相比标准的FCM分割算法和遗传模糊聚类算法,分割效果更好。
模糊C-均值聚类;遗传算法;粒子群算法;邻域像素;核磁共振成像
0 引 言
由于医学图像含有的噪声高,而且各种组织之间边界比较模糊,且组织内部的灰度很不均匀,对比度也相对较低,所以采用传统的分割技术很难达到预期的效果[1]。针对这些问题,将FCM算法(Fuzzy C-Means)广泛应用在这类图像的分割中,国内外专家也对FCM算法应用在医学图像分割领域做了大量研究,
并且取得了一定的基础研究成果,为后续研究提供了一定的参考。
FCM算法是1974年由Dunn[2]在硬C均值算法的基础上提出的,轰动一时,很多专家都参与了研究。在同一年,BEZEDEK[3]又进行了一般化的推广,建立了一套比较完善的FCM算法的基础理论。1980年,BEZEDEK进一步对FCM算法的收敛性进行了证明[4]。由于FCM算法对初始聚类中心比较敏感,所以文献[5]提出将遗传算法(GA)应用于FCM算法中,通过GA优秀的全局寻优能力来确定FCM算法中的聚类数目并寻找到一组全局最优的聚类中心,也就是GA-FCM算法[5]。鉴于其有较好的分割效果,GA-FCM算法应用范围很广泛[6-8]。
由于FCM算法的目标函数仅仅考虑了像素的灰度信息,所以对异常值和噪声比较敏感。刘晓妮等[9]采用FCM算法和离散正则化算法相结合的分割方法,首先用标准FCM算法对目标图像进行初始分割,再将得到的分割图像采用半监督的离散正则化算法进行二次分割,但是算法的计算复杂度较大,分割效率也变低了。文献[10-13]也对模糊聚类使用遗传算法进行改进,但算法复杂度太高。
针对上述问题,在寻找最优初始聚类中心时,文中在传统的粒子群算法中同时加入遗传算法中的两个算子,交叉算子和变异算子,使得两个算法的优势互补,克服粒子群算法容易陷入局部最优的缺陷,为后续分割提供更精确的初始聚类中心;同时引入像素的标号场和特征场信息,重新构造传统FCM算法的目标函数,加强邻域像素和聚类中心像素间的作用强度,克服仅仅考虑像素的灰度信息而导致对噪声和异常值敏感的问题,从而得到更精准的分割结果。
1 标准FCM算法
FCM算法是一种模糊、无监督的聚类算法,它的分类是柔性的,而且实现简单,所以应用广泛。简言之,FCM算法将像素的灰度值作为一个参数,把每个像素到聚类中心像素的欧氏距离作为相似性测度,然后使得欧氏距离的加权取最小值,从而进行图像数据的聚类。FCM算法根据欧氏距离的加权方式,把目标函数定义为:
(1)
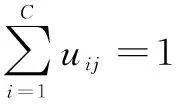
目标函数J的物理意义表示目标图像中的每个像素到各聚类中心加权距离的平方和。当目标图像中的每个像素点到某个聚类中心的欧氏距离加权值最小,而距离其他聚类中心的欧氏距离尽量大时,FCM算法的基本原则是寻找到一组合适的聚类中心和隶属度矩阵,使得目标函数J取得最小值min(J)。
通过求目标函数的最小值可以得到uij(i=1,2,…,C),uij是第j个像素隶属于不同聚类的隶属度;最后将每个像素划分到不同的类中,把第j个像素划分到第k类的划分公式如下[14]:
k=argmax{uij,i=1,2,…,C}
(2)
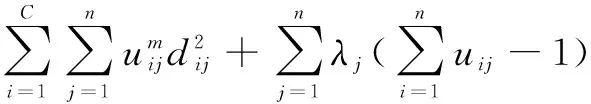
(3)


(4)
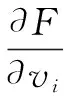
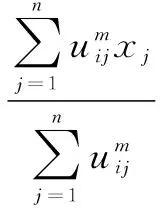
(5)
在计算目标函数的最小值时,需要根据式(4)和式(5)不断更新隶属度矩阵和聚类中心,直到求得最小值为止。在目标函数取得最小值时,保留此时的隶属度,根据式(2)对目标图像的每个像素进行分类,从而得到图像的分割结果。在迭代过程中要选取合适的迭代终止条件,这里不能根据目标函数前后两次迭代的差值小于某个阈值就停止迭代,这样使得算法很容易陷入局部最优,得不到理想的分割结果。标准的FCM算法一般是根据前后两次迭代的像素的隶属度的差值小于某个设定的阈值就停止迭代,因为隶属度更新和聚类中心有关,当初始聚类中心选取不恰当时算法容易陷入局部最优;也可以设置一个最大迭代次数,到达迭代次数时立即停止迭代。
通过上述的推导分析,可以将FCM算法分割图像的过程总结为:
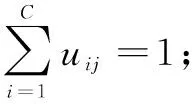
(2)根据式(5)计算像素的聚类中心vi(i=1,2,…,C);
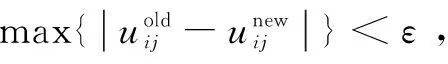
(5)根据式(2)对图像中的每个像素进行分类,输出分类后的图像。
从式(1)可知,要使目标函数取得最小值,就需要保证目标图像中的像素离它最近的聚类中心的隶属度尽可能大,而属于其他聚类中心的隶属度尽可能小。
2 改进算法
在使用FCM算法进行分割前,利用遗传-粒子群算法寻找一组最优的初始聚类中心,在粒子群算法中引入遗传算法的交叉算子和变异算子。交叉算子充当的作用是使成对的粒子之间可以互相交流信息,提高粒子往新的方向搜索的能力,而变异算子是用来提高粒子群算法跳出局部最优的能力,并保留粒子群算法中的种群分割策略来保持种群的多样性,克服粒子群容易陷入局部最优的缺陷。其中将FCM算法的目标函数的倒数作为遗传-粒子群算法的适应度函数的一个参数,适应度函数为:
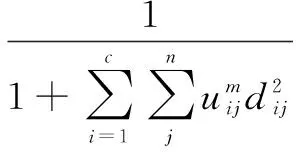
(6)
其中,J为标准FCM算法中的目标函数。由此可知,当遗传-粒子群算法中的适应度函数F的取值越大时,聚类效果就越好[16]。
通过引入邻域像素标号场和特征场,重构目标函数,加强邻域像素和聚类中心像素之间的作用强度,有利于削弱异常值和噪声对分割结果的影响,得到更准确的分类结果。文中通过马尔可夫理论引入邻域像素的标号场信息。从理论上讲,相邻像素之间有很大的可能具有相同的标号,用Nj表示第j个像素的邻域,则像素j划分为聚类i的先验概率可以表示为[17]:
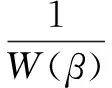
(7)
其中,lj表示第j个像素的标号;β表示邻域像素的作用强度;W(β)表示将先验概率转化到0到1之间的归一化项;U(lj=i|β)表示能量函数,为方便,下文将用πij表示。
为了更好地表示第j像素与聚类i之间的关系,采用式(8)作为新的非相似性测度:
dij=-logp(xj|lj=i)
(8)
根据上述的分析和推导,可以将改进算法的目标函数定义为:

(9)
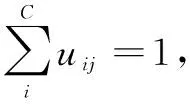
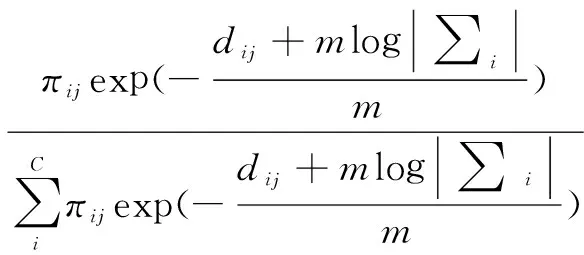
(10)
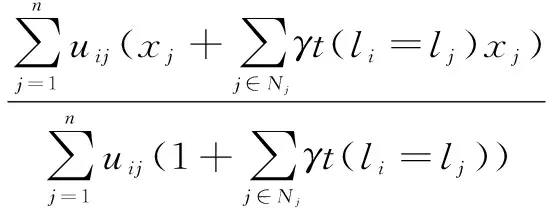
(11)
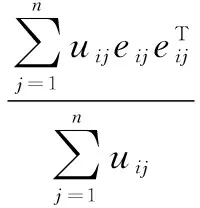
(12)
其中,eij定义为:

(13)
其中,γ表示邻域像素的作用强度;t(li=lj)表示一个指数函数。
综上,文中改进算法的步骤为:
(1)设置算法中的初始值,包括聚类中心数目C、模糊因子m、先验概率中的β、最大迭代次数K、特征场作用强度γ和迭代停止条件θ;
(2)根据GA-PSO确定一组最优的初始聚类中心,并根据式(4)初始化隶属度矩阵U(0);
(3)根据式(7)、(11)、(12)分别计算每个聚类中的先验概率、均值u(k)和协方差∑(k);
(4)根据式(10)更新隶属度矩阵U(k);
(5)如果{U(k+1)-U(k)}<θ或者到了最大迭代次数,则停止,否则令k=k+1,转步骤(3)继续进行迭代运算。
3 实验结果及分析
将改进算法应用到比较有代表性的MRI脑部图像分割实验中,目标图像是一幅大小为256×256的灰度图像。因为人脑的MRI图像主要包括脑脊液、脑白质、脑灰质和背景四个部分,所以将聚类数目取4,模糊因子取2,分别用标准的FCM算法、遗传模糊聚类算法和文中算法对其进行分割,结果如图1所示。
从图1可以看出,传统FCM算法和遗传模糊聚类算法受噪声影响,分割结果不是很理想,有很多细小和模糊的部分,存在明显的噪声干扰;而遗传模糊算法相比传统算法分割效果较好;文中算法因为加入了邻域像素作用,使得算法抗噪性能得到了较大提升,分割结果也相对更加精确。
分割参数如表1所示。其中Vpc为BEZDEK划分系数,是一个衡量FCM算法聚类效果的参数,主要目的是对分割后像素的隶属度进行刻画。该指标的定义如下:
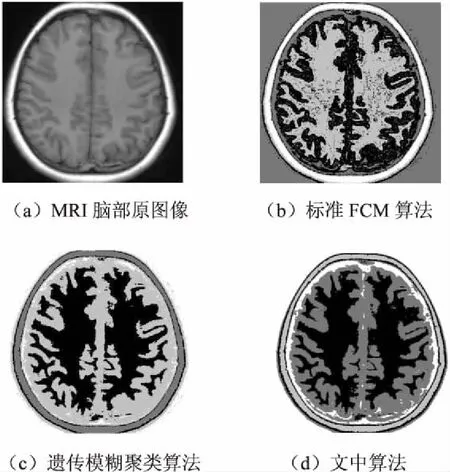
图1 各算法分割结果
(14)

表1 分割参数对比
一般而言,对于目标图像中的每个像素点来说,一个聚类效果好的算法会使它属于其中一类的隶属度尽可能大而属于其他类的隶属度尽可能小。因此,一个聚类算法的Vpc越大,说明这个聚类算法的效果越好。表1中,传统的FCM算法的Vpc比遗传聚类算法和文中算法都要小,而遗传聚类算法和文中算法的Vpc相近,但是文中算法的迭代次数相比遗传聚类算法少了很多,比传统FCM算法的迭代次数也相对较少。因此,文中算法可以有效解决传统FCM算法对聚类中心初始值、图像中的噪声以及异常值敏感的缺陷,分割结果改善明显。
4 结束语
在标准的FCM算法及其改进算法的基础上,通过结合遗传算法和粒子群算法来寻找最优的初始聚类中心,减少了算法的迭代次数;同时引入了特征场和标号场,重新构造FCM算法中的目标函数对目标图像进行分割,使得算法的抗噪性能得到了一定的提升。但是文中算法还有一些参数需要依赖人工经验选取,比如模糊因子、标号场以及特征场作用强度参数,下一步的研究中将寻找一种合适的方法来自动选取最优参数,从而将图像的半自动化分割转为完全自动化分割。
[1] 张 翡,范 虹.基于模糊C均值聚类的医学图像分割研究[J].计算机工程与应用,2014,50(4):144-151.
[2] DUNN J C.A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters[J].Journal of Cybernetics,1973,3(3):32-57.
[3] BEZEDEK J C.Pattern recognition with fuzzy objective function algorithm[M].New York:Plenum Press,1981.
[4] CANNON R L,DAVE J V,BEZDEK J C.Efficient implementation of the fuzzy C-means clustering algorithms[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1986,8(2):248-255.
[5] VIJAYACHITR S,TAMILARSI A,KASTHURI N.Multiple input single output (MISO) process optimization using[C]//International conference on education technology and computer.Singapore:IEEE,2009:248-252.
[6] LIU Suhua,HOU Huifang.A combination of mixture genetic algorithm and fuzzy c-means clustering[C]//International symposium on IT in medicine & education.Ji’nan,China:IEEE,2009:254-258.
[7] BELAHBIB F Z B,SOUAMI F.Genetic algorithm clustering for color image quantization[C]//3rd European workshop on visual information processing.Paris,French:[s.n.],2011:83-87.
[8] BEZDEK J C, EHRLICH R, FULL W. FCM:the fuzzy c-means clustering algorithm[J].Computer and Geosciences,1984,10(2):191-203.
[9] 刘晓妮,卢奕南,雷 玲.基于FCM和离散正则化的多目标图像分割[J].计算机辅助设计与图形学学报,2015,27(1):142-146.
[10] 张永库,尹灵雪,孙劲光.基于改进的遗传算法的模糊聚类算法[J].智能系统学报,2015,10(4):627-635.
[11] 杨 凯,蒋华伟.模糊C均值聚类图像分割的改进遗传算法研究[J].计算机工程与应用,2009,45(33):179-182.
[12] 邱双双.基于核模糊C-均值聚类与阈值分割的SAR影像分割算法[J].科技创新与应用,2014(35):15.
[13] 张佳骕,蒋亦樟,王士同.基于特征选择聚类方法的稀疏TSK模糊系统[J].智能系统学报,2015,10(4):583-591.
[14] 张自嘉,岳邦珊,潘 琦,等.基于蚁群和自适应滤波的模糊聚类图像分割[J].电子技术应用,2015,41(4):144-147.
[15] 宋娈娈.一种基于图像滤波的加权FCM图像分割算法[J].商丘师范学院学报,2014,30(12):10-14.
[16] 张红旗,王春光,李海军.基于遗传算法的草莓图像FCM分割方法研究[J].农机化研究,2015(4):55-57.
[17] 赵雪梅,李 玉,赵泉华.结合高斯回归模型和隐马尔可夫随机场的模糊聚类图像分割[J].电子与信息学报,2014,36(11):2730-2736.
AnOptimalAlgorithmforMedicalImageSegmentationBasedonFuzzyC-MeansClustering
LIAO Lin-feng,QIU Xiao-hui
(School of Communication and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
Fuzzy C-Means Clustering (FCM) has a good effect in the segmentation of fuzzy medical images.By setting the initial cluster center,the division is carried out according to the membership degree of each pixel,and segmenting results are obtained by means of iteration.Aiming at the problem that FCM is susceptible to initial value of cluster center and noise,the genetic algorithm and particle swarm algorithm are combined to determine a set of suitable initial clustering centers.After combination,the convergence rate of initial clustering center is accelerated than that of only use of genetic algorithm.Then the objective function of standard FCM is reconstructed by introducing neighborhood information of pixels so as to improve the similarity between the neighborhood and the center pixel,which makes the adjacent pixels more divided into the same class and overcomes the problem that the standard FCM only considers the gray value between the pixels and causes the sensitivity to noise and outliers.The proposed method is applied into the MRI brain image segmentation experiment which shows that it is superior to the standard FCM and genetic algorithm on segmentation effect.
Fuzzy C-Means clustering;genetic algorithm;particle swarm optimization;neighborhood pixels;nuclear magnetic resonance imaging
TP301.6
A
1673-629X(2017)12-0081-04
10.3969/j.issn.1673-629X.2017.12.018
2016-12-11
2017-04-13 < class="emphasis_bold">网络出版时间
时间:2017-09-27
江苏省自然科学基金(BK2011789);东南大学毫米波国家重点实验室开放课题(K201318)
廖林峰(1992-),男,硕士研究生,研究方向为图像处理;邱晓晖,博士,教授,研究方向为图像处理。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170927.0957.020.html
