核范数随机矩阵求解新方法及其RPCA应用

王 臻，杨 敏

(南京邮电大学 自动化学院，江苏 南京 210023)

核范数随机矩阵求解新方法及其RPCA应用

王 臻，杨 敏

(南京邮电大学 自动化学院，江苏 南京 210023)

RPCA(稳健主成分分析)从原始观测数据中恢复低秩成分和稀疏成分。RPCA常用交替方向法迭代求解，算法的效率取决于核范数优化求解，即SVD分解。而RPCA在计算机视觉应用中，图像和视频等巨大的数据量为大规模数据SVD分解带来了很大困难。采用随机矩阵算法对SVD分解进行改进，分别为计数缩略算法、标准随机k-SVD算法和快速随机k-SVD算法。主要是对原有大规模数据矩阵进行降维随机采样，使用随机投影算法得到原数据矩阵的一个近似，对这个近似矩阵进行QR分解，得到对应的酉矩阵。对酉矩阵进行相关操作，得到与原矩阵SVD相似的结果。算法的时间效率和存储空间得到极大改善。基于单张图像和视频前景检测等仿真实验，表明所提方法大大提高了RPCA迭代优化求解的效率。

稳健主成分分析；交替方向法；标准随机k-SVD；快速随机k-SVD

0 引 言

PCA在高维数据样本中寻找和挖掘低维特征空间。在较小的高斯随机噪声时，可通过奇异值分解准确求解。当不满足上述条件时，所得结果会有很大偏差，于是用RPCA来解决此种情况。RPCA即低秩矩阵恢复[1]，又称为稀疏与低秩矩阵分解[2]。

RPCA模型(稳健主成分分析)[3]在视频前景提取、人脸识别图像预处理等计算机视觉领域中应用广泛。求解RPCA常用交替方向法[4]，充分利用RPCA模型具有的很好的可分离结构特性，是对带有线性约束条件凸规划问题的增广拉格朗日乘子法的一种改进。算法每次迭代的主要计算量在于SVD分解[5]。像矩阵求逆、特征值分解、奇异值分解等这些矩阵计算，不但非常耗时，存储所需的空间也很大，因此，这些缺点限制了它的拓展和应用范围。为了对一个大规模的矩阵进行计算，随机矩阵近似技术[6]应运而生。随机矩阵计算已经在现代数据科学领域占有举足轻重的地位。特别在过去的十年里，随机数字线性代数取得了卓越进步，现在大规模的矩阵计算不再是一个不可完成的任务了。

文中将改进的SVD分解，即随机矩阵算法应用到视频图像的前景检测中。对于交替方向法中每次迭代时，对核范数的优化求解，即大规模SVD分解，进行优化改进，对于大规模的数据矩阵进行随机近似求解，大大提高了算法效率。数据表明，改进算法具有更快的计算速度和存储优势。

1 RPCA模型及交替方向法求解算法

1.1 RPCA模型

RPCA问题可以抽象描述[7]为：已知观测数据矩阵M，且M=L+S，而L和S是未知的，但是已知L为低秩，S为稀疏且非零元素可以任意大，要求恢复L。基于问题的描述，首先想到的解决方法是寻求观测数据中主成分L的最小秩，且干扰误差矩阵S是稀疏的，即非零元素个数较少。于是形成了如下优化问题：

(1)

其中，‖·‖0表示S中非零元的个数。

通过对式(1)做松弛变化，可以把问题转化为一个易于解决的凸优化问题，即用1范数代替0范数，用L的核范数代替L的秩。式(1)转化为：

(2)

这个凸优化问题，在一定条件下，可以求解并能得到理想的恢复结果(L,S)，且解是唯一的。

1.2 交替方向法

交替方向法面向目标函数可分解[8](即为两个不同变量凸函数的和)、带线性约束和凸集约束的问题，它是Lagrange乘子法的一种变形。先构造问题的增广Lagrangian函数，然后通过交替极小化增广Lagrangian函数来更新两个变量，最后更新Lagrange乘子，如此迭代。其好处是更新变量子问题要比原问题简单，甚至有闭解。

对于稳健PCA问题(式(2))，易得其增广拉格朗日函数为：

Γ(L,S,Y)=‖L‖*+λ‖S‖1+〈Y,L+S-

(3)

其中，Y∈Rm×n为线性约束乘子；μ>0为标量，是违背线性约束的惩罚参数；〈·〉表示标准内积；‖·‖F表示Frobenius范数。

很明显，可以直接运用经典增广拉格朗日乘子法求解，其迭代主题是：

(4)

每个迭代是一个大型的非光滑优化问题。经典的增广拉格朗日乘子法把式(2)看作一个一般的最小化问题，而忽视了它在目标函数和约束条件中都体现出的很好的可分离结构特性，即式(4)是同时最小化L和S的。

而对于S的极小化是非常容易得到的：

(5)

对于L的极小化也很容易得到：

(6)

交替更新，可以得到结果：

(7)

其中，prox是在如下空间的欧几里得投影：

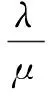
(8)

惩罚参数比较适合于动态调整，从相关文献[9-11]可以了解具有动态变化参数的交替方向法的收敛性以及一些具体有效的调整参数的方法。

交替方向法求解RPCA问题(式(4))时，算法效率取决于每一次迭代的核范数优化求解，即大规模的SVD分解。因此，SVD算法的好坏对于交替方向法处理大规模矩阵的稀疏和低秩矩阵恢复问题有很重要的影响。

2 随机矩阵算法

在对矩阵进行操作前，通常会对大规模矩阵进行降维操作。矩阵的降维方式一般有随机投影和列选择两种方式[12]。假设给定一个矩阵A∈Rm×n，而S∈Rn×s是一个缩略矩阵，比如是一个随机投影或者是列选择矩阵[13]，C=AS∈Rm×s是A的一个缩略。矩阵C的大小是远小于矩阵A的，但是C却保存了矩阵A的一些重要性质。文中使用的降维方式主要是使用随机投影中的计数缩略算法[14]。

算法1：计数缩略算法。

输入矩阵A∈Rm×n及缩略矩阵的列数s；

初始化C为一个m×s的全零矩阵；

Fori=1,2,…,ndo；

(1)随机均匀采样矩阵C的l个列向量；

(2)随机均匀采样g个+1或者-1；

(3)通过将矩阵C的第l个列的各元素加上g×矩阵A的第i个列向量来更新矩阵C的第l个列；

End For

得到缩略矩阵C∈Rm×s。

该算法有以下一些性质：

(1)时间复杂度为O(nnz(A))

(2)空间复杂度为O(ms)。当矩阵A不适合存储时，该算法将矩阵C保存在内存中，并且只经历一次矩阵A的各列向量。

(3)理论保证

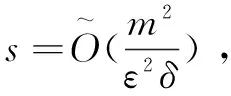
(4)计数矩阵缩略算法在矩阵A是稀疏矩阵时特别有效。

3 改进的SVD算法

3.1 标准随机k-SVD算法

本节描述标准随机k-SVD算法[15]，它计算矩阵A的k-SVD分解并且到达了1+ε的F范数相对误差。算法描述如下：

算法2：标准随机k-SVD算法。

输入：目标秩k和矩阵A∈Rm×n；

S∈Rn×s，C=AS∈Rm×s

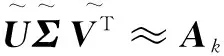
(9)

算法推导：

由于C的列空间和QC的列空间是一样的，式(9)的极小化问题就可以被等价转换为：

(10)

(11)

该算法有以下几个特性：

(1)该算法只有2次经过A；

(3)时间复杂度为O(nnz(A)k/ε)。

3.2 快速随机k-SVD算法

标准算法将大多数时间花费在解决式(10)上。假如式(10)可以更高效地解决，那么标准随机k-SVD可以变得更加迅速。可以注意到，可以通过不精确的最小二乘回归算法[17]解决式(10)的问题。

现在构造一个m×p大小的计数缩略(或者是高斯投影+计数缩略)矩阵P来解决这个问题：

(12)

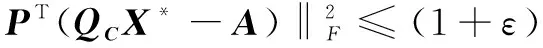
(13)

算法描述如下：

算法3 ：快速随机k-SVD算法。

输入：目标秩k和矩阵A∈Rm×n；

构造一个n×s计数缩略矩阵S，然后令C=AS；

构造一个m×pcs的计数缩略矩阵Pcs，还有一个pcs×p的矩阵Psrht；

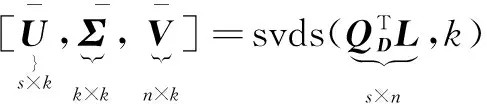
算法推导：

(14)

基于此，通过式(15)进行分解。

(15)

这里需要注意：

(1)该算法只经过2次矩阵A；

(2)算法的时间复杂度为O(nnz(A)+(m+n)poly(k/ε))；

(3)参数应该满足k

(4)算法中的缩略算法也可以使用其他的矩阵缩略方式；

(5)矩阵A，矩阵sketch，矩阵L这些都是整个系统中存储花销最大的，但是幸运的是，它们只需要1次或2次扫描。假如矩阵A，缩略矩阵，矩阵L不适合随机存储，那么它们应该被存储到硬盘中，再逐个部分被加载到内存中进行计算。

4 仿真实验

4.1 单张图像分解仿真

测试图像为MATLAB自带图片，其大小为512*512。如图1所示，前10个奇异值中，奇异值的衰减速度相当快，并且逐渐趋向于0，图像表现为低秩矩阵。现分别使用SVD算法、标准随机k-SVD算法以及快速随机k-SVD算法进行低秩矩阵重建仿真，比较算法之间的运行效率、恢复精度，以及与目标秩之间的关系。

图1 奇异值衰减图解

重建结果与原图的比较如图2所示。

图2 三种SVD分解效果图

这是分别使用三种SVD算法，利用主成分累加和逼近原图，得到原图的低秩逼近效果图。可以看出，三种算法都很好地实现了对于原矩阵的处理。

图3为标准随机k-SVD算法和快速随机k-SVD算法的计算精度随目标秩变化的曲线。

图3 两种改进算法的精度比较

由图3可以看出，标准随机k-SVD算法的分解精度要比快速随机k-SVD算法高。随着目标秩的升高，两种随机算法的精度都逐渐提高并趋向平稳。

图4为三种SVD算法的计算时间随目标秩的变化曲线。

图4 三种算法的计算时间比较

由图4可以看出，两种改进算法的计算时间都随目标秩的增加而增加。由于快速随机k-SVD每次计算都需要构造好几个缩略矩阵，所以在目标秩一定的情况下，标准随机k-SVD比快速随机k-SVD用时短。而MATLAB自带的SVD每次计算的时间几乎是不变的，比两种改进算法都要耗时。

4.2 视频前景提取仿真

待操作数据矩阵大小为20 800*200，取视频中的4帧。取目标秩k为50，并且同时构造出原矩阵的缩略矩阵C，其中s取60。仿真结果如图5所示。

图5 视频前景提取效果

对于快速随机k-SVD算法，同样先构造缩略矩阵C，p和pcs分别取100和80，取值条件需满足k

如图5所示，第一行是视频中的4帧数据。第二行是文中改进算法对每帧数据分解得出的低秩部分，即背景。最后一行是分解得出的稀疏部分，即视频的运动前景。可以看出，改进算法都较好地实现了视频前景与背景的分离。

三种SVD算法的比较如表1所示。

表1 三种SVD算法的比较

从表1的运行结果可以看出，两种改进的随机k-SVD分解与普通的SVD分解一样也实现了前景和背景的分离。标准随机k-SVD算法虽然迭代次数比普通的SVD算法要多一些，但是运行时间却大幅缩短，并且由于采用缩略矩阵算法，程序对于内存的占用也相对较少，很好地实现了算法的改进。快速随机k-SVD算法虽然每次迭代的时间比标准随机k-SVD算法要长一些，因为快速随机k-SVD算法中进行了多次的矩阵缩略降维，但是其迭代次数比普通的SVD算法和标准随机k-SVD算法都要少，运行时间也更短。虽然该算法中使用了多个缩略矩阵，比较占内存，但幸运的是，它们只需1次或2次的扫描就可以实现算法的功能。实验结果证明，该算法也有良好的收敛性，提高了核范数求解的效率。

5 结束语

针对RPCA模型中用来实现图像前景和背景分离的交替方向法，对矩阵算法进行了研究和改进。通过分析，当用交替方向法求解RPCA问题时，每次计算量消耗最大的就在于核范数的优化求解，即大规模SVD的计算。于是介绍了随机矩阵算法，并提出了两种新的随机SVD算法。两种算法都大大提高了代码的运行效率，并且经过仿真实验表明，两种算法达到的实际分离效果和普通的SVD分解也相差无几。总之，两种改进的随机奇异值分解算法都加快了算法的收敛速度，很好地提高了算法效率，并且都不需要占用大量的内存空间。

[1] Candès E J,Li X,Ma Y,et al.Robust principal component analysis[J].Journal of the ACM,2011,58(3):11-12.

[2] Lin Z,Chen M,Wu L,et al.The augmented Lagrange multiplier method for exact recovery of a corrupted low-rank matrices[R].Illinois:University of Illinois at Urbana-Champaign,2010.

[3] 江明阳,封举富.基于鲁棒主成分分析的人脸子空间重构方法[J].计算机辅助设计与图形学学报,2012,24(6):761-765.

[4] Yuan X,Yang J.Sparse and low-rank matrix decomposition via alternating direction methods[R].Hong Kong:Hong Kong Baptist University,2009.

[5] Wang Ruoxi, Li Yingzhou, Mahoney M W,et al.Structured block basis factorization for scalable kernel matrix evaluation[J].Numerische Mathematik,2015,83:313-323.

[6] Mahoney M W.Randomized algorithms for matrices and data[J].Foundations and Trends in Machine Learning,2013,3(2):647-672.

[7] 戴琼海,付长军,季向阳.压缩感知研究[J].计算机学报,2011,34(3):425-434.

[8] 彭义刚,索津莉,戴琼海,等.从压缩传感到低秩矩阵恢复:理论与应用[J].自动化学报,2013,39(7):981-994.

[9] He B S,Liao L Z,Han D,et al.A new inexact alternating directions method for monontone variational inequalities[J].Mathematical Programming,2002,92(1):103-118.

[10] He B S,Yang H.Some convergence properties of a method of multipliers for linearly constrained monotone variational inequalities[J].Operations Research Letters,1998,23(1):151-161.

[11] Kontogiorgis S,Meyer R R.A variable-penalty alternating directions method for convex optimization[J].Mathematical Programming,1998,83(1):29-53.

[12] Clarkson K,Woodruff D P.Low rank approximation and regression in input sparsity time[C]//Proceedings of annual ACM symposium on theory of computing.[s.l.]:ACM,2013:121-128.

[13] Woodruff D P.Sketching as a tool for numerical linear algebra[J].Foundations and Trends in Theoretical Computer Science,2014,10(1-2):1-157.

[14] Wang Shusen,Zhang Zhihua,Zhang Tong.Towards more efficient symmetric matrix sketching and cur matrix decomposition[J].Journal of Machine Learning Research,2015,13:2729-2769.

[15] Halko N,Martinsson P G,Tropp J A.Finding structure with randomness:probabilistic algorithms for constructing approximate matrix decompositions[J].SIAM Review,2011,53(2):217-288.

[16] Gorinov S A,Tyrtyshnikov E E.The maximum-volume concept in approximation by low-rank matrices[J].Contemp. Math.,2001,280:47-51.

[17] Halko N.Randomized methods for computing low-rank approximations of matrices[D].Colorado:University of Colorado,2012.

ANewMethodforSolvingNuclearNormwithRandomMatrixandItsApplicationinRobustPrincipalComponentAnalysis

WANG Zhen,YANG Min

(College of Automation，Nanjing University of Posts and Telecommunications，Nanjing 210023，China)

RPCA (Robust Principal Component Analysis) recovers sparse and low rank components from the original observation data.It commonly uses ADM (Alternate Direction Method) for iterative solving,the efficiency of which depends on the nuclear norm optimization solution,that is SVD.The application of RPCA in computer vision,large amounts of data from images and video make it difficult for large-scale data SVD.Therefore,a random matrix algorithm is adopted to improve the SVD,respectively the algorithm of count sketch,the prototype randomizedk-SVD and the faster randomizedk-SVD.Its main idea is to reduce the size of the original large-scale data matrix and sample randomly.Using the random projection algorithm to obtain an approximation of the original matrix,and operating QR decomposition of this approximate matrix,the unitary matrix corresponding to it is obtained,and then the results which is similar to the SVD can be achieved through correlated operation of unitary matrix.The time and space of the algorithm have been greatly optimized.Simulation based on single image and video foreground detection shows that the proposed method can greatly improve the efficiency of RPCA iterative optimization.

RPCA;ADM;prototype randomizedk-SVD;faster randomizedk-SVD

TP391

A

1673-629X(2017)12-0071-06

10.3969/j.issn.1673-629X.2017.12.016

2016-10-21

2017-02-23 < class="emphasis_bold">网络出版时间

时间：2017-08-01

国家自然科学基金资助项目(61271234)

王 臻(1992-)，男，硕士，研究方向为核范数极小化随机优化求解；杨 敏，博士，副教授，研究方向为计算机视觉与图像理解。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170801.1550.022.html