基于社交网络信息的协同过滤推荐算法

张朝恒，何小卫，陈勇兵

(浙江师范大学 数理与信息工程学院，浙江 金华 321000)

基于社交网络信息的协同过滤推荐算法

张朝恒，何小卫，陈勇兵

(浙江师范大学 数理与信息工程学院，浙江 金华 321000)

随着互联网数量的不断增多，海量的数据信息为互联网用户带来了便利，同时也给推荐系统带来了技术性的挑战。用户-评分矩阵对传统的协同过滤算法具有关键性的作用，然而在大数据时代的背景下，用户面对海量的数据信息，很难对自己喜欢的项目全部进行评分，这就造成了评分数据的稀疏，从而影响推荐算法的精度性。针对数据稀疏问题，利用社交网络信息，分别从用户评分、兴趣标签、社交关系三个方面分别建立用户相似度模型，然后采用协同过滤算法将三个模型进行融合，以进行推荐预测。在KDD CUP 2012 Track1数据集上进行实验。实验结果表明，该算法相比传统的协同过滤算法，算法精确度有较好的提高，对于数据稀疏问题也有较好的缓解作用。

协同过滤；推荐系统；相似度模型；标签信息；社交关系

0 引 言

随着互联网技术的日趋成熟，以信息化服务产业以及电子信息产业为代表的互联网数量越来越多，如新闻资讯、百科系统、电子商务以及社交网络等。这些网站大多拥有巨大的用户量，随之带来的是海量的数据信息。现如今，人们已经进入大数据时代，用户很难从海量的数据信息中快速找到自己所需要的信息，不同的用户利用搜索引擎往往得到的是相同的推荐排名结果，然而用户更希望根据自己的兴趣喜好得到个性化推荐。以亚马逊网上书店、淘宝网、京东商城，天猫超市等为代表的电子商务网站，以及以YouTube、腾讯微博、FaceBook、人人网等为代表的社交网络平台大都采用个性化推荐，而传统的推荐系统已经很难满足用户需求。因此，许多学者提出了多种推荐算法，其中协同过滤算法以其良好的扩展性和可实现性[1]，在推荐系统中被广泛应用。然而协同过滤推荐自身也存在着许多缺点，主要包括：(1)数据稀疏问题。由于用户-项目评分矩阵数据的稀疏性，计算出的用户或项目相似度必定是不准确的，进而影响到推荐精度以及用户的体验效果。(2)冷启动问题。在推荐系统中由于新用户没有对项目的评分信息，而新项目也没有被用户评分，这就无法计算其相应的最近邻，因此无法推荐。(3)传统算法计算只能区分用户间的兴趣程度，对于用户间的朋友关系与陌生程度却不能区分。

一方面，传统的协同过滤算法过分依赖评分信息，而忽略其他因素，如用户的标签信息，这些标签信息本质上体现了用户对某些项目上的偏好程度[2-3]。如何更好地利用这些信息，建立用户相似度模型，对实现个性化推荐以及提高算法的精确度有着重要作用。

另一方面，许多推荐系统都基于这样一个假设：用户对于项目的评分是相互独立的，用户主观地根据自己的兴趣爱好对项目进行评分，而不会受到其他用户的影响。然而，在现实生活中，大多数用户当决定选择某项项目时，一般都会向自己信任的朋友或社交网络中亲密的好友征求意见，人们的兴趣爱好通常容易受到朋友圈中好友或现实中亲人的影响。用户的社交关系在一定程度上反映了他们在兴趣爱好上的相似程度以及他们在现实世界的相似程度。社交网络作为一种信息传播媒介，为人们提供了一个交流、学习、娱乐的社会平台，其中比较出名的有腾讯微博、FaceBook、YouTube、微信、朋友圈等。这些网络平台提供了丰富的用户关系以及朋友关系信息。近年来，利用社交网络信息来提高推荐系统的性能越来越受到学者们的关注[4-6]。例如：Ziegler和Lausen发现在社交平台中用户间的信任度与相似度成正相关性[7-9];Massa和Avesani利用Epinions网络上的信息计算用户的信任关系来预测用户兴趣偏好[10]。如何合理地利用社交网络信息，产生个性化推荐，对推荐系统精度的提高以及用户体验都有重要意义[11-13]。

1 相关工作

1.1 传统算法介绍

目前大多数网站都是根据用户的喜好为其提供个性化的推荐，例如亚马逊、易趣网等，这些网站大都采用协同过滤算法[14]。基于用户的协同过滤算法的主要步骤如下：

(1)计算用户间的相似度。

(2)依据目标用户与其他用户的相似度从大到小排序，选出前N个用户作为其最近邻。

(3)利用最近邻对其进行评分预测。

用户间的相似度计算可采用多种方式，其中最常用的是皮尔逊相关系数[15]。给定用户a与用户b，相似度计算如式(1)所示：

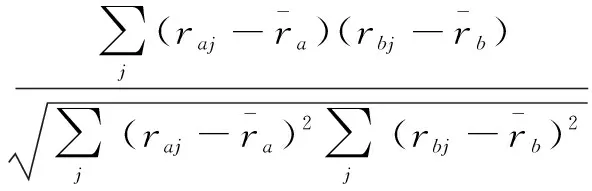
(1)

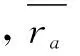
通过皮尔逊相关系数计算用户间相似度，然后选取目标用户最近邻，记Nur是其最近邻，最后计算其对项目i的预测评分，如式(2)所示：

(2)

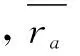
(3)

其中，Si为所有项目集合；ruj为用户u对项目j的评分。

传统的推荐算法基于用户之间的评分是相互独立的，忽略了社交网络中用户间的信任关系以及现实生活中用户间的朋友关系，然而通常情况下，用户选择某项项目时，一般会征求其好友的建议或意见。为了提高推荐精度，社交网络信息与用户评分信息在社交推荐系统中应该同时被考虑[16-18]。在现实生活中，用户可以向自己关系密切，并且信任的好友表达自己的兴趣偏好，同样，他们的兴趣爱好也会对其所信任的好友有不同程度的影响，因此通过用户间信任度，可以对用户偏好进行预测。Golbeck在社交网络中研究了用户间的信任度，并且通过用户间信任度进行预测推荐[19]，这些利用信任关系的推荐系统比传统推荐更具个性化。

1.2 模型定义

传统的协同过滤通常利用评分信息计算用户间相似度，记SR={Sij}，其中Sij表示用户i与用户j的相似度，SR表示用户间相似度矩阵。根据协同过滤，用户u对项目j的预测评分可以表示成关于SR的函数，记为Puj=f(SR)。

提取用户标签信息，计算基于用户标签信息的相似度矩阵，记Sk={Sij}，然后采用协同过滤算法，用户u对项目j的评分预测记为Puj=f(Sk)。

同样依据用户社交关系信息，计算基于社交关系的用户相似度矩阵，记Ss={Sij}，然后同样采用协同过滤算法，用户u对项目j的评分预测可记为Puj=f(Ss)。

为了能够得到较好的推荐结果，将三种模型进行融合。为了方便表示，每个模型定义如下：

UB：基于评分矩阵模型。

KW：基于社交网络用户标签模型。

SNS：基于社交网络用户社交关系模型。

UK：结合UB模型与KW模型。

US：结合UB模型与SNS模型。

UKS：结合UB模型、KW模型与SNS模型。

文中提取社交网络中的标注信息，其中用户对项目的标注信息均为二值标注，这里的标注值相当于用户对项目的评分值，然后采用基于用户的协同过滤算法进行评分预测。

1.3 基于用户标签信息相似度模型的推荐(KW模型)

在社交网络中，用户通常会选用一些关键词来表示自己的职业、兴趣爱好以及观点，这一系列的关键词被称为用户的标签。用户的标签是用户的自我描述，例如：运动、乒乓、游泳、唱歌、旅游等。用户的标签信息反映了用户的兴趣趋向，在某种程度上用户标签的相似性反映了用户兴趣的相似性。提取所有的用户关键词形成一个用户-关键词字典，令N表示字典中关键词的总个数，给定一个用户a，其关键词的向量形式如式(4)所示：

uka={ka1,ka2,…,kan}

(4)

利用杰卡德相关系数计算基于用户标签信息相似度，用户a与用户b的相似度计算如式(5)所示：

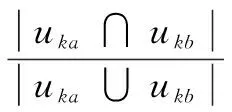
(5)

然后选取目标用户u最近邻，记Nuk为基于用户标签最近邻，然后预测评分，如式(6)所示：

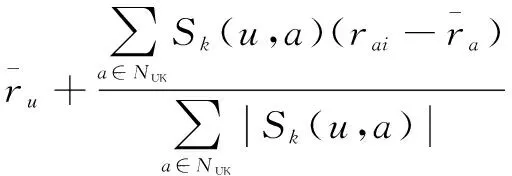
(6)

1.4 基于用户社交关系的相似度模型的推荐(SNS模型)

社交网络中用户的社交关系主要反映在用户的关注关系上。关注关系在社交平台上普遍存在，例如：腾讯QQ、微信、微博等社交平台。除了关注关系，还包括点赞、打赏、绑定账号等特殊的社交关系方式。关注关系作为一种普通的社交关系，在某种程度上反映了用户间的相互支持认同、信任等关系。如果用户a关注用户b，具体说来主要有两个原因：第一，在现实世界中，用户a与用户b本来就是朋友关系；第二，用户a对用户b发表或转发的内容感兴趣，因此关注了用户b，而用户b发表或转发的内容本身也反映了b的兴趣。a关注了b，在一定程度上反映了a与b具有相近的兴趣偏好。

同样地，如果用户a关注了用户c，用户b关注了用户c，那么就可以认为一定程度上用户a与用户b也有相似的兴趣爱好。根据用户间的关注信息进行建模，给定一个用户a，记用户a在一段时间内关注过其他用户的集合为：

fa={fa1,fa2,…,fan}

(7)

同样利用杰卡德相关系数计算用户社交关系的相似度，如式(8)所示：

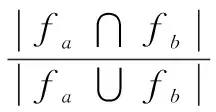
(8)

同样选取与目标用户u最近邻，记为Nus为基于社交关系的最近邻，然后依据协同过滤算法预测评分，如式(9)所示：

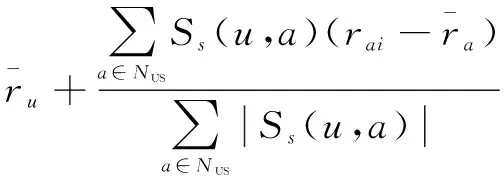
(9)

2 基于社交网络信息的协同过滤算法

通过评分信息可以很容易找到目标用户的最近邻，但由于评分矩阵的稀疏性，利用式(1)计算用户间的相似度存在一定的偏差。

2.1 融合社交网络用户标签信息的协同过滤模型(UK模型)

如果用户a与用户b共同评论的数量非常少而且评价的分值又高度相近，由式(1)计算的用户a与用户b的相似度就很高[20]。例如：a与b只对项目i进行评分，且评分分值相同，通过式(1)计算得到a与b的相似度为1。如果把b作为a的最近邻用户，利用b的评分信息来预测a的评分，这就会对a的预测评分造成一定的影响，也就是说，a与b虽然拥有相同的项目评分，但是只利用单一的用户-项目评分矩阵计算用户相似度无法准确地反映用户间的兴趣爱好程度。

基于上述情况，从社交网络中提取用户标签信息，挖掘用户的兴趣偏好，建立用户相似度模型。给定一个用户u，记Nuk为利用社交网络中用户关键词信息计算的用户u的最近邻，然后利用Nur和Nuk两个最近邻进行评分预测，将基于评分信息的协同过滤与基于用户标签的协同过滤相融合，如式(10)所示：

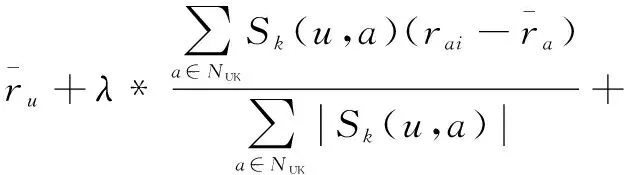
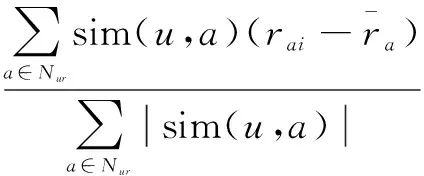
(10)

在一定程度上，该算法能够对上述情况起到缓解作用，其中参数λ表示KW模型在UK模型中的权重。

2.2 融合社交网络用户社交关系信息的协同过滤模型(US模型)

相反地，如果用户a与用户b在现实世界中是好朋友，但由于矩阵稀疏，用户a与用户b没有评分的项目非常少甚至没有，通过式(1)计算出用户a与用户b的相似度就相当低。因为用户b是用户a的朋友，用户b的评分对用户a的预测评分有着重要影响，但是用户a与用户b的相似度过低，使得用户b不在用户a的最近邻内，这就造成了用户a最近邻用户的缺失，进而影响推荐精度。

基于上述可能出现的情况，运用社交网络中用户的社交关系信息建立用户相似度模型，然后获取目标用户的最近邻。给定一个用户u，记Nus为基于用户社交关系计算的最近邻，然后在传统协同过滤算法的基础上融合基于用户社交关系的协同过滤，利用Nur和Nus两个最近邻进行评分预测，对传统的协同过滤算法进行补充，如式(11)所示：

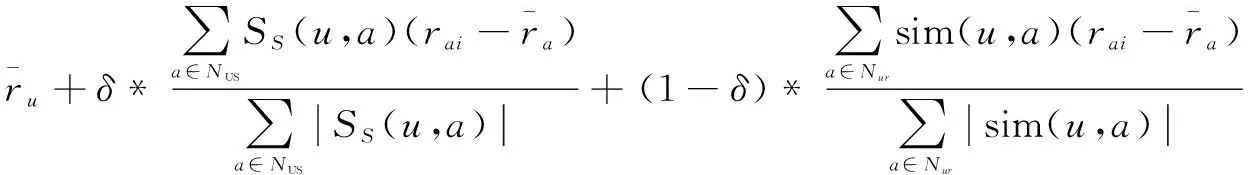
(11)

其中，参数δ表示SNS模型在US模型中的权重。在一定程度上，该算法能够对上述情况起到缓解作用。

2.3 融合社交网络信息的协同过滤算法(UKS模型)

基于上述两种情况，融合基于评分矩阵相似度模型(UB模型)、基于用户标签相似度模型(KW模型)、基于用户社交关系相似度模型(SNS模型)来提高推荐精度，如式(12)所示：

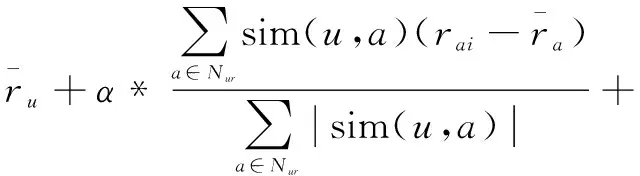
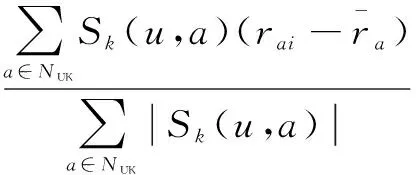
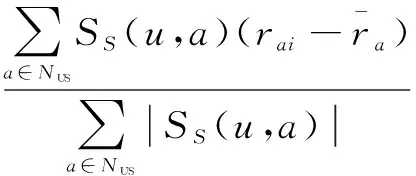
(12)

其中，α，β，γ为参数，有α+β+γ=1。

3 算法的时间复杂度与精度分析

3.1 算法时间复杂度分析

传统的协同过滤算法，即UB模型算法的时间复杂度是O(n2)，而基于KW模型算法与SNS模型算法的时间复杂度也都为O(n2)，所以KW模型、SNS模型、UB模型的时间复杂度相当。由于UKS模型是由以上三种模型进行线性组合，因此，基于UKS模型的算法时间复杂度与传统的UB模型算法的时间复杂度相当。

3.2 数据集

为了验证算法的有效性，选取KDD CUP 2012 Track1(www.kddcup2012.org)作为数据集。该数据集是2012年腾讯公司提供的关于腾讯微博用户数据的一个真实采样，其中主要使用三个数据集。

标注信息数据集：包含1 392 873个用户，4 710个项目，以及42 118 498条标注信息，标注信息均采用二值标注，其中标注值均为1或-1，每个标注信息还有一个时间戳。

用户关键词数据集：包含2 320 895个用户的关键词信息，每个用户不同的关键词都用不同特定的正整数表示。

用户社交关系数据集：包含50 655 143条用户关注信息，每个用户与被关注的用户都用特定的数字作为其索引号。

标注信息数据集稀疏程度计算如下：

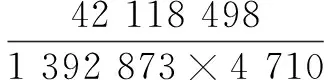
由此可以看出该数据集十分稀疏。

由于原数据集中数据规模过于庞大，因此从中选取10万条标注信息作为训练集，其中包括3 162个用户，3 365个项目。在原测试集中缺少真实的评分数据，为了确保实验的精确度，将对选出的数据做以下处理：从10万条数据信息中随机筛选出90%作为训练集，剩下10%作为测试集，为了实现算法的实验评估，在测试集中确保每个用户至少有3个正标注信息。

3.3 算法评估

在实验中，采取平均精度(Mean Average Precision atN,MAP@N)来评价推荐算法的精度。首先计算测试集中每个测试用户的精度，然后将每个测试用户的精度进行累加，最后寻求精度平均值。具体来说：给定一个测试用户u,L是按照推荐算法预测评分高低排序为用户u推荐的项目列表，每个测试用户精度AP@N定义如式(13)所示：

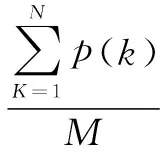
(13)

其中,M为推荐列表L中被测试用户标注过的项目总数；p(k)为推荐列表L中第k位置处的精度，定义如式(14)所示：

(14)

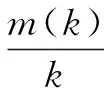
(15)

其中，U表示测试集中所有用户的集合。

在KDD CUP 2012 Track1任务中，N值取3作为实验评估标准。为了更好地与其他实验进行比较，文中也取N为3作为实验评估标准。

3.4 模型最佳TOP-N及模型参数分析

为了寻找每个模型最近邻最佳个数，将运用训练集对UB,KW,SNS三种单因素模型进行训练，通过改变最近邻个数来观测对算法精度的影响，进而寻找每个模型的最佳邻居个数。选取TOP-N从2到20来观察精度的变化，实验结果如图1所示。

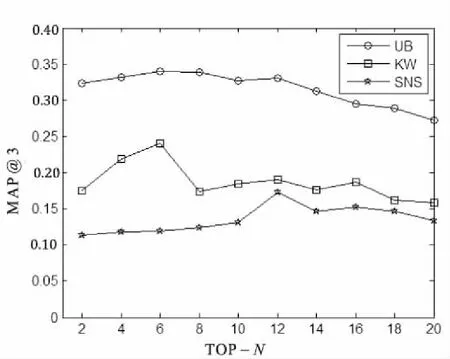
图1 三种模型TOP-N对精度的影响

从图1中可以看出，在KW，SNS模型中，算法精度MAP@3先随着TOP-N的增加而增加，然而当TOP-N超过某个值后精度反而减少，最后趋于平稳。而在UB模型中，当TOP-N从0到6逐渐增加时，算法精度有所提高，但当TOP-N从6到20变化时，算法精度大体呈现下降趋势。同时还可以观察出，当TOP-N分别为6、6、12时，UB，KW，SNS模型算法精度MAP@3相应最高，因此UB，KW，SNS三种模型的最佳TOP-N分别为6,6,12，对应UB，KW，SNS三种模型最佳精度值分别为0.340 2,0.240 0,0.173 0。由此可知，UB模型有着较高的推荐精度，KW模型次之，然后是SNS模型。为了提高算法的推荐精度，将对UK模型中的参数λ,US模型中的参数δ，以及UKS模型中的参数α，β，γ进行实验，寻找各个模型中的参数最佳值。

3.4.1 寻找UK，US模型中的最佳参数λ，δ

在UK模型中，为了评估KW模型在UK模型中所占的权重，将对模型中参数λ值取步长为0.1进行实验。当λ=0时，表示只依赖于UB模型进行评分预测；当λ=1时，表示只利用KW模型进行评分预测；当参数λ∈(0,1)，表示融合UB模型与KW模型来进行评分预测。

在US模型中，参数δ为SNS模型在US模型中的权重。当δ=0时，表示只依赖于UB模型进行评分预测；当δ=1时，表示只利用SNS模型进行评分预测；当参数δ∈(0,1)，表示融合UB模型与SNS模型进行评分预测。对于参数δ，步长也取0.1，实验结果如图2所示。

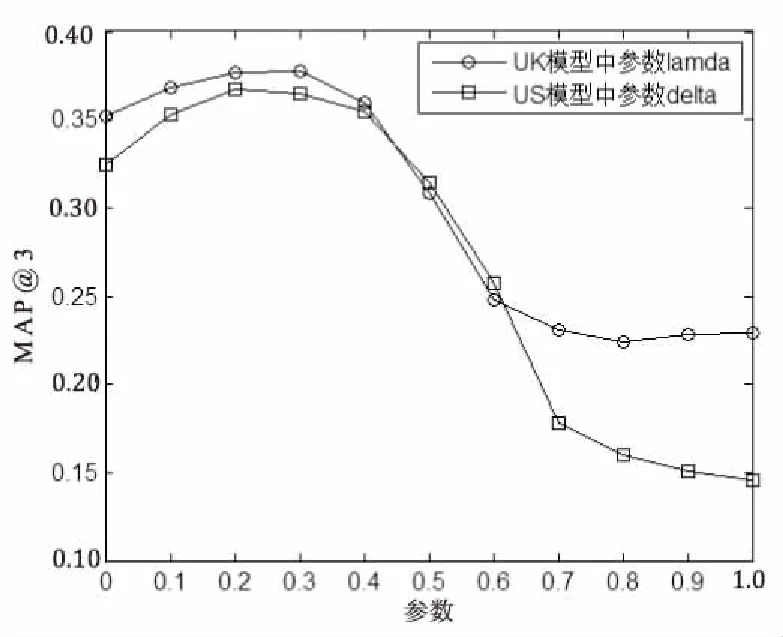
图2 UK模型中参数λ，US模型中参数δ对精度的影响

从图2中可看出，在UK模型下，当参数λ从0到0.3变化时，算法精度MAP@3逐渐呈上升趋势，当参数λ进一步从0.3到1不断增大时，算法精度反而逐渐下降，然后趋于平稳。同时还可以观察到，当λ=0时，算法精度明显高于λ=1的算法精度值，说明单一的UB模型在精度上要高于KW模型。从算法精度MAP@3变化趋势来看，当参数λ在0.2到0.4之间的范围内时，基于UK模型的算法精度较高，当参数λ=0.3时，算法精度MAP@3最高。

在US模型下，当参数δ从0到0.2变化时，算法精度逐渐呈上升趋势，随着参数δ进一步从0.2增加到1，算法精度MAP@3逐渐降低，然后趋于平稳。当δ=0时，算法精度MAP@3明显高于δ=1时的算法精度，这也说明单一的UB模型精度也要高于SNS模型精度。从算法精度MAP@3的变化趋势来看，当参数δ在0.1到0.3之间，基于US模型算法的精度较高，当参数δ=0.2时算法精度MAP@3最佳。

3.4.2 寻找UKS模型中的最佳参数α，β，γ

在UKS模型中,为了评估UB，KW，SNS模型各自在UKS模型中的权重，将分别对参数α，β，γ进行实验。考虑到在UB，UK,US模型中，UB模型的推荐精度相比KW,SNS模型较高，且由α+β+γ=1，只需寻求β，γ两个参数即可。

根据图1，选取UB，KW，SNS每个模型最佳邻居数进行实验，即UB模型TOP-N为6，KW模型TOP-N为6，SNS模型TOP-N为12。当寻求参数α最佳值时，先固定参数α，γ，参数β步长采用0.1来进行实验；同样对于参数γ，先固定参数α，β，步长也采用0.1，实验结果如图3所示。

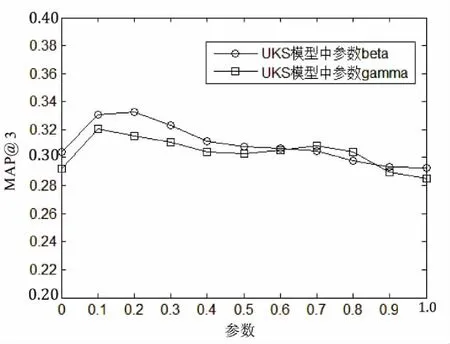
图3 UKS模型中参数β，γ对精度的影响

从图3可以看出，当参数β从0到0.2逐渐增加时，算法精度MAP@3也随之增加，随着β从0.2到1继续增加，算法精度先降低，然后趋于平稳。而对于参数γ，当从0到0.1范围内变化时，精度MAP@3提高较快，当从0.1到1逐渐增加时，精度MAP@3先降低，然后趋于平稳。同时还可以观察到，当参数β，γ从0.4到1变化时，算法精度MAP@3趋于平稳，也说明随着参β，γ数值的增大，KW模型与SNS模型对UKS模型的影响逐渐减弱。因此得到如下结论：在UKS模型下，当参数β=0.2，参数γ=0.1时，算法精度最高。

3.5 实验结果分析

为了检验各个模型的最佳精度，将在各个模型参数取得最佳的情况下进行测试。在UK模型中参数λ取0.3，在US模型中参数δ取0.2，在UKS模型中参数α，β，γ分别取0.7,0.2,0.1。仍然选取TOP-N从2到20来观察算法精度的变化，实验结果如图4所示。

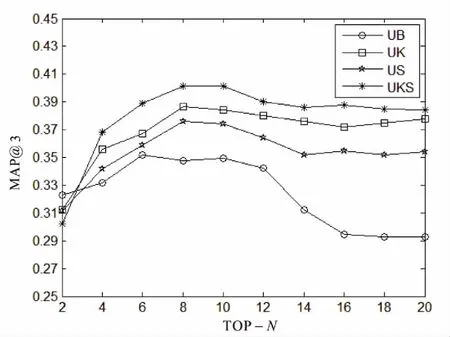
图4 UB，UK，US，UKS的TOP-N对精度的影响

从图4中可以看到，当TOP-N从4到20变化时，模型UK，US，UKS的精度都大于UB模型的精度，表明融合社交网络信息的UKS模型算法要比单一的依据评分信息的UB模型算法，在推荐精度方面有较好的提高，并且UKS模型的算法精度最优，UK模型次之，然后是US模型。也验证了表1中单因素KW模型较优于单因素SNS模型。同时还可以观察到，在UB模型中，随着TOP-N从12到20变化，算法精度MAP@3急剧下降，然而在UK,US,UKS模型中，算法精度相对趋于平稳，表明基于社交网络信息的KW，SNS模型对UB模型有较好的补充作用。

为了精确计算UK,US,UKS模型对于UB模型提高的精度，定义计算方式如下：

(16)

表1US，UK，UKS三种模型与UB模型的精度比较及提高比率

从表1中可以看出，US模型相比UB模型提高了8.70%，UK模型相比UB模型提高了10.50%，显然UK模型要优于US模型。表明在UB模型的基础上融合不同的单因素模型对算法会有不同的影响，也验证了图1中在单因素模型下KW模型要优于SNS模型。随着影响模型因素的增加，算法精度也有不同程度的提高，其中UKS模型精度最高，相比UB模型精度提高18.01%。UKS模型在UB模型的基础上融合了KW和SNS，而UK,US两个模型相比UB模型，只分别融合了KW，SNS单个模型。实验结果表明：在UB模型上融合KW，SNS两个模型要优于融合单因素模型。

通过以上实验可以得出如下结论：融合多因素模型的算法精度要优于单因素模型，然后将多因素UKS模型与另外两种算法—SHANDA[21]和UST[22]作比较。UST，SHANDA也相应融合了多因素分解模型，比较结果如图5所示。

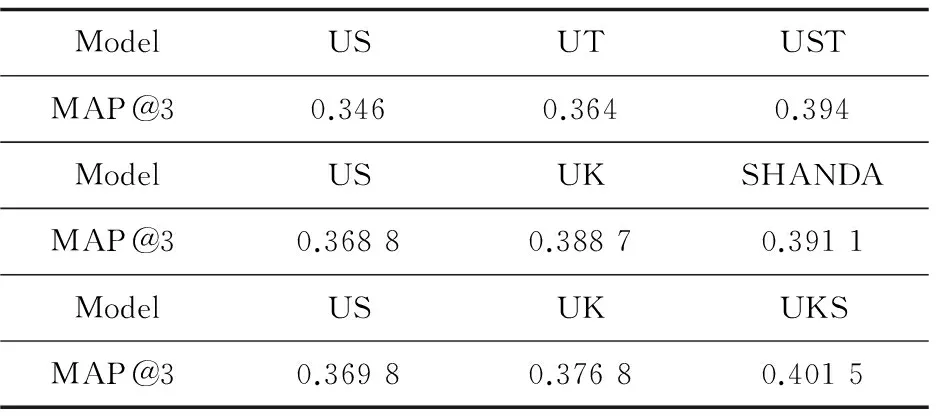
ModelUSUTUSTMAP@30.3460.3640.394ModelUSUKSHANDAMAP@30.36880.38870.3911ModelUSUKUKSMAP@30.36980.37680.4015

图5 UKS、SHANDA、UST三种模型的精度比较

通过比较可知，在UK模型中的文中算法精度高于UST模型中UT模型的精度，而略低于SHANDA模型中UK模型的精度，然而在US和UKS模型中，文中算法精度仍然比其他两种模型算法的精度要高。相比其他两种算法，UKS模型对于推荐精度有较好的提高。相比传统的协同过滤算法，在用户评分数据稀疏的情况下，提取用户的标签信息、用户社交关系信息来计算用户间的相似度，进而预测评分，对传统算法中数据稀疏问题有很好的补充作用，对于推荐精度也有很好的提高。

4 结束语

分析了多种因素模型对推荐精度的影响，包括用户标注信息、用户标签信息，以及用户在社交平台上的社交关系信息，利用这些信息提出一种融合社交网络信息的协同过滤算法。实验结果表明，相比传统的UB模型，在数据稀疏的情况下，UKS模型对其有很好的缓解作用，与SHANDA和USTCF两种推荐算法相比，算法精度都有所提高。不足之处在于参数的寻找问题。对于不同的数据集，取得参数的最佳值可能存在一定的偏差，这就需要抽取不同的数据集进行实验，才能寻求更加准确的最佳值。下一步的工作将是抽取不同的数据集对算法中的参数进行多次实验，寻找更加精确的参数值，进一步提高算法推荐精度。

[1] Herlocker J L,Konstan J A,Terveen L G,et al.Evaluating collaborative filtering recommender systems[J].ACM Transactions on Information Systems,2004,22(1):5-53.

[2] 陈博文,刘功申,张浩霖,等.融合标签传播和信任扩散的个性化推荐方法[J].计算机工程,2014,40(12):33-38.

[3] 张艳梅,王 璐.适应用户兴趣变化的社会化标签推荐算法研究[J].计算机工程,2014,40(11):318-321.

[4] Ma H,Yang H,Lyu M R,et al.Sorec:social recommendation using probabilistic matrix factorization[C]//Proceedings of the 17th ACM conference on information and knowledge management.[s.l.]:ACM,2008:931-940.

[5] Ma H,King I,Lyu M R.Learning to recommend with social trust ensemble[C]//Proceedings of the 32nd international ACM SIGIR conference on research and development in information retrieval.[s.l.]:ACM,2009:203-210.

[6] Liu F,Lee H J.Use of social network information to enhance collaborative filtering performance[J].Expert Systems with Applications,2010,37(7):4772-4778.

[7] Ma H,Zhou D,Liu C,et al.Recommender systems with social regularization[C]//Proceedings of the 4h ACM international conference on web search and data mining.[s.l.]:ACM,2011:287-296.

[8] Ziegler C N, Lausen G. Analyzing correlation between trust and user similarity in online communities[C]//Second international conference on trust management.[s.l.]:[s.n.],2004.

[9] 定明静.基于信任网络的推荐技术研究及应用[D].成都：电子科技大学，2013.

[10] Massa P,Avesani P.Trust-aware recommender systems[C]//Proceedings of the 2007 ACM conference on recommender systems.[s.l.]:ACM,2007.

[11] 蔡 浩，贾宇波，黄成伟.结合用户信任模型的协同过滤推荐方法研究[J].计算机工程与应用，2010,46(35)：148-151.

[12] 朱丽中,徐秀娟,刘 宇.基于项目和信任的协同过滤推荐算法[J].计算机工程,2013,39(1):58-62.

[13] 杨兴耀,于 炯,吐尔根·依布拉音,等.基于信任模型填充的协同过滤推荐模型[J].计算机工程,2015,41(5):6-13.

[14] Linden G,Smith B,York J.Amazon.com recommendations:item-to-item collaborative filtering[J].IEEE Internet Computing,2003,7(1):76-80.

[15] Adomavicius G, Tuzhilin A. Personalization technologies:a processoriented perspective[J].Communication of the ACM,2005,48(10):83-90.

[16] Shardanand U,Maes P.Social information filtering:algorithms for automating word of mouth[C]//Proceedings of the SIGCHI conference on human factors in computing systems.[s.l.]:ACM,1995:210-217.

[17] Ma H.An experimental study on implicit social recommendation[C]//Proceedings of the 36th international ACM SIGIR conference on research and development in information retrieval.[s.l.]:ACM,2013:73-82.

[18] Wu L,Chen E,Liu Q,et al.Leveraging tagging for neighborhood-aware probabilistic matrix factorization[C]//Proceedings of the 21st ACM international conference on information and knowledge management.[s.l.]:ACM,2012:1854-1858.

[19] Golbeck J.Generating predictive movie recommendations from trust in social networks[C]//International conference on trust management.[s.l.]:[s.n.],2006:93-104.

[20] Wang Bailing,Huang Junhen,Qu Linbing,et al.A collaborative filtering algorithm fusing user-based,item-based and social network information[C]//IEEE international conference on big data.[s.l.]:IEEE,2015:2337-2343.

[21] Chen Y,Liu Z,Ji D,et al.Context-aware ensemble of multifaceted factorization models for recommendation prediction in social networks[C]//Proceedings of the KDD-Cup workshop.Beijing,China:[s.n.],2012:1-7.

[22] Wang Rui,Wang Bailing,Huang Junhen.A collaborative filtering algorithm based social network information[C]//IEEE international conference on big data.[s.l.]:IEEE,2015:2384-2389.

ACollaborativeFilteringRecommendationAlgorithmBasedonSocialNetworkInformation

ZHANG Chao-heng，HE Xiao-wei，CHEN Yong-bing

(School of Mathematics and Information Engineering,Zhejiang Normal University,Jinhua 321000,China)

With the increasing number of Internet，massive data information offers convenience for Internet users and also brings a technical challenge to the recommendation system.User rating matrix plays a key role on the traditional collaborative filtering algorithm.However,in the age of big data,it is difficult for users to score all items they love when facing massive data information,resulting in the sparse rating data,which affects the accuracy of the recommendation algorithm.For data sparsity，the user similarity models are established respectively from three aspects of user score,interest tags and social relationship by using the social network information and then collaborative filtering algorithm is applied to complete the three models integration for recommending prediction.It is experimented in the data set of KDD CUP 2012 Track1 that the algorithm proposed is improved in the accuracy compared with the traditional one,and also has good ease for the data sparsity.

collaborative filtering;recommendation system;similarity model;tags information;social relationships

TP301.6

A

1673-629X(2017)12-0028-07

10.3969/j.issn.1673-629X.2017.12.007

2016-12-03

2017-04-12 < class="emphasis_bold">网络出版时间

时间：2017-08-01

国家自然科学基金资助项目(61572023)；浙江省自然科学基金(LY14F010008)

张朝恒(1990-)，男，硕士研究生，研究方向为协同过滤、机器学习；何小卫，副教授，硕士生导师，研究方向为机器学习、图像视频处理。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170801.1556.072.html