基于分时电价的家庭智能用电控制策略研究
2017-12-19重庆邮电大学唐玉玲
重庆邮电大学 唐玉玲 应 俊
基于分时电价的家庭智能用电控制策略研究
重庆邮电大学 唐玉玲 应 俊
0 引言
随着科技的发展,智能电表、传感器以及智能控制设备的相应出现[1],人们的家庭生活更加智能化。与生活相关的电子设备可以连接在一起,通过设备间的协调运行,为人们提供舒适的生活环境与优质的居住体验,提供更加高效、便捷、丰富的家用基础服务[2]。同时,用户可以建立智能用电控制平台,优化用电情况,降低用电量,提高用电效率,节约成本[3]。鉴于此,本文基于分时电价,针对家庭用户的智能用电设备的能耗进行分析,得到最优家用电器控制策略,实现家庭智能用电,节省电能。
1 算法分析
家庭智能用电控制的系统框架主要包括智能控制中心、智能电表、智能开关、智能插座以及家庭用电设备[4]等,智能电表可采集到家庭用电器的用电数据。用户可根据自己的需求,设定家用电器的运行状态,以电量消费最小为目的找到家用电器最合理的使用模式,然后通过智能家庭网关实现对家用电器的控制。
为了智能控制第二天的家庭用电情况,需要预测第二天的用电信息,包括电器的启动时间、运行时长等。本文利用自适应模糊推理系统(ANFIS),通过对家庭用电器历史使用数据的学习,对第二天的用电情况进行预测,预测家庭用电器的开启时间,运行时间等信息,从而有针对性的对用电器进行控制。
ANFIS综合了神经网络的学习算法和模糊推理的简洁形式,通过对训练数据的学习,产生数值解。既具有学习机制,又具有模糊系统的语言推理能力。
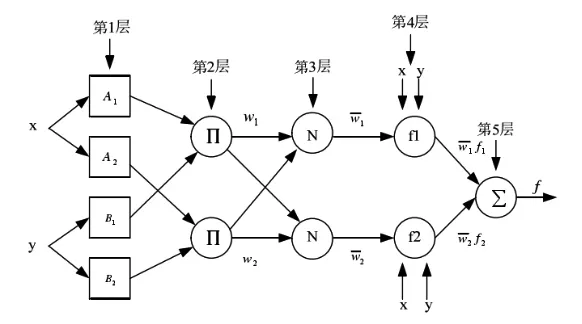
图1 自适应模糊推理系统示意图
ANFIS结构有5层,如图1所示, 第一层是输入参数的选择和模糊化,它是模糊规则建立的第一步。模糊集的隶属度函数,通常选用钟型函数,三角隶属函数,梯度隶属函数等都是模糊化时常用的函数。第二层是模糊规则激励强度的计算,将输入信号的隶属度相乘。第三层是节点进行各条规则适用度的归一化计算。 第四层是每个节点作为自适应节点。第五层的单节点是一个固定节点,计算所有输入信号的总输出。
遗传算法是一类借鉴生物界自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象[6],在每次迭代中都保留一组候选解,并按照某种指标从解群中选取较优的个体,利用遗传算子对这些个体进行组合,产生新一代的候选解群,重复此过程直到满足某种收敛条件为止。对待优化的问题,先求取目标函数,然后根据目标函数设定适应度函数,根据设定的目标函数,利用MATLAB软件中的遗传算法工具箱求解函数优化问题,从而得到家庭用电最优方法。在尽量不影响用户每天正常的用电需求情况下,付出电费最少作为优化目标。
2 仿真分析
实验采用的数据是一个家庭每天的用电数据,3个电表以每分钟的采样频率采集。电表1记录采集到的厨房电量,包括微波炉、烤箱等;电表2采集洗衣机电量;电表3采集热水器和空调电量。实验采用的分时电价以武汉试点地区的电价标准,电价采取《国家发展改革委关于湖北省分时电价方案的批复》文件中的电价方案[5],其中,“峰段电价=平段电价*1.8;谷段电价=平段电价*0.48”,分时电价函数为:

2.1 用电行为预测
为了对第二天的家用电器进行调控,需要提前知道家用电器的运行情况,开启时间、运行时间等,所以需要对第二天的家用电器运行情况进行预测。本文利用MATLAB中的ANFIS工具箱进行仿真,预测结果与实际使用情况进行比较,得到预测匹配情况图,如图2(a)(b)所示:
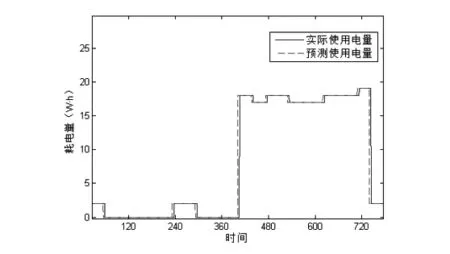
图2 (a) 预测匹配度图
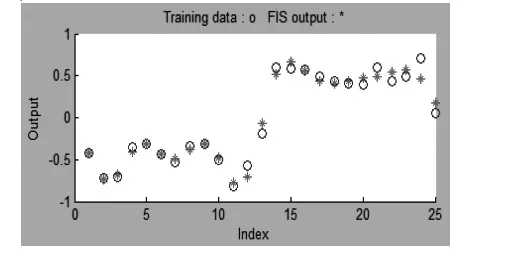
图2 (b) 预测匹配度图
2.2 智能用电策略
在尽量不影响用户每天正常的用电需求情况下,付出电费最少为优化目标。将一天的时间划分为120个时间段,每个时间段12分钟,其中,u表示各个时段。则目标函数为:
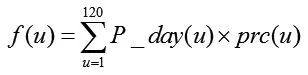
一天120个片段,在采用二进制编码时只需要采用7位二进制码(128的二进制码是1111111),为算法带来了方便。根据时间的划分原则,每种用电设备的用电量可以也能够一个向量来表示,假设向量A代表所有用电设备的集合,a代表任何一种用电设备,Pa代表用电设备a的能耗向量。
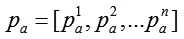
Pan代表用电设备在1个时间片段内的能耗,如果在这个时间片段不工作,则能耗为0。
设备的总的能耗为:
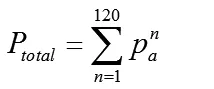
设定一种用电设备的功率值(p)是定值,在12分钟的时间片段内的能耗表示为:
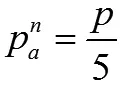
在分时电价的情况下,智能用电优化算法通过优化用电设备的能耗Pa来达到节省用电费用的目的,需要为每种用电设备规划合理的工作时间范围。假设αa()是用电设备工作时间范围下限,是工作时间范围上限,,la为a的工作时长,,ta为a的起始工作时间,则。

将预测得到的数据,进行优化仿真分析。利用负荷分类的模型,对用电器进行用电优化。总能耗为:
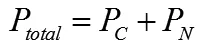
其中,PC是参与调控电器的总电量。
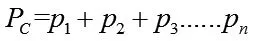
P是参与调控的单个电器电量消耗,PN为未参与调控的电器能耗。
普通情况下和采用智能用电优化情况下的用电量分布如图3(a)(b)所示:
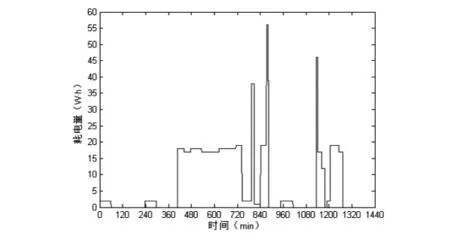
图3(a) 普通情况下的用电量分布图
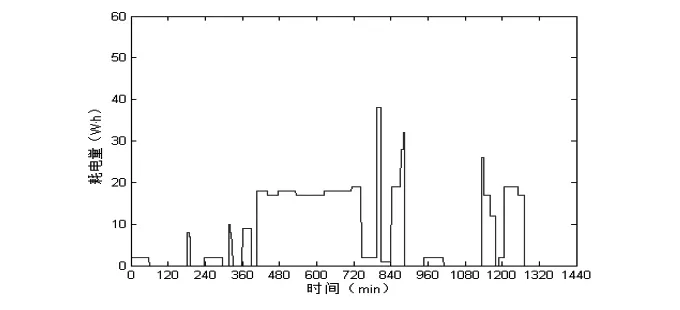
图3(b) 采用智能用电优化情况下的用电量分布图
从利用遗传算法进行仿真的进化图4中可以看出,设置好遗传参数后,在12代左右可获得最优解。最优解和解的平均值一开始相差比较大,随着种群数的不断进化,适应度值小的个体被淘汰,而最优解个体被保留,最终得到最优解和解的平均值相当的情况,即为最终的最优解。
对于一般的家庭用户而言,用电量主要分布在早上、中午、晚上三个时间段。经过智能优化后,用电量的分布时间比优化前分散。主要是将用电设备从电价高的时间段调整到平时间段或者谷时间段,从而达到节省用电费用的目的。
通过图5的分时电价,可以计算出家庭用电费用。未优化前,用电费用为7.349元,智能优化后,用电费用为5.673元,用电费用减少了22.81%。文献[6]中的用电费用,优化前为9.18元,优化后为7.56元,减少了17.65%。本论文的方法与其进行对比,用电费用减少得更多,更利于节省用电费用。
3 结论
本文提出了一种基于分时电价情况下的家庭智能用电控制策略。该方法在满足用户满意度的条件下,尽可能地减少用户用电费用。利用自适应模糊推理算法 (ANFIS) 预测第二天电器参与运行的情况,通过遗传算法分析最优的用电费用模型。综合考虑用户的用电满意度和电费节省情况,对家庭用电器提出智能控制方案。通过MATLAB仿真,结果验证了提出的方案可以在满足用户满意度的条件下,节省较多的用电费用。
[1]张新昌,周逢权.智能电网引领智能家居及能源消费革新[J].电力系统保护与控制,2014(5):59-67.
[2]Zhuang Zhao,Won Cheol Lee.An Optimal Power Scheduling Method for Demand Response in Home Energy Management System[J].IEEE Transactions on smart grid,2013,4(3):1391-1400.
[3]Amjad Anvari-Moghaddam,Ashkan Rahimi-Kian.Optimal Smart Home Energy Management Considering Energy Saving and a Comfortable Lifestyle[J].IEEE Transactions on smart grid,2017,6(1):324-332.
[4]樊玮,刘念,张建华.事件驱动的智能家庭在线能量管理算法[J].电工技术学报,2016,31(13):130-140.
[5]A.Nacer,B Marhic.Smart Home,Smart HEMS,Smart heating:An overview of the latest products and trends[C].2017 6th International Conference on System and Control(ICSC),2017,90-95.
[6]傅军栋,康水华,马书研.基于尖峰电价的家庭能量管理最优控制算法[J].计算机应用研究,2016,33(7):2083-2086.
唐玉玲(1991—),硕士研究生,主要从事电子新技术及应用方面的研究。
应俊(1976—),副教授,硕士生导师,主要从事电子信息技术方面的研究。
