基于复杂网络理论的电力网络关键线路识别
2017-12-19邹艳丽
傅 杰,邹艳丽,谢 蓉
(广西师范大学电子工程学院,广西 桂林 541004)
基于复杂网络理论的电力网络关键线路识别
傅 杰,邹艳丽,谢 蓉
(广西师范大学电子工程学院,广西 桂林 541004)
从复杂网络理论角度出发,提出了一种基于网络凝聚度的电力网络关键线路评价方法。方法着重关注电力网络的全局状态,综合考虑电力网络中各节点之间的连通能力,以及网络中节点的数目,通过观察输电线路断开前后电力网络凝聚度的变化量,来衡量电力网络中各输电线路的重要程度。通过将研究的计算结果与文献中已有的基于网络效率的关键线路评价方案的结果进行对比,以及在拓扑结构和动力学角度上进行仿真验证,均说明了提出的关键线路衡量方法是合理且有效的。
复杂网络;凝聚度;电力网络;关键线路;拓扑结构;动力学
0 引言
近年来,随着电力网络[1]传输容量的不断增加、输电范围的不断扩大,由输电线路故障导致的大规模的电网事故频繁发生[2-5],对人们的生产和生活造成了严重的影响。利用复杂网络理论知识[6-8],对电力网络中的关键线路实现快速定位,并采取针对性的保护措施,能够提高系统供电的可靠性[9-10],减小电力系统大停电事故发生的概率。
经过多年的研究,学者们基于复杂网路理论,从网络的架构、线路的特性、网络的输电效率[11]、功率输送关系[12]以及系统的运行状态[13]等方面,对电力网络的脆弱性进行了大量的仿真实验分析[14-16],提出了许多电力网络关键线路识别的方法[17-18],但是这些方法都是针对某些特定的问题提出来的,分别从不同的角度来说明线路的重要性,各自判断的侧重点有所不同,都有着一定的优点以及缺点,这类方法都对电力网络全局状态的考虑相对较少,这给下一步的深入研究指出了方向。
本文从复杂网络理论的角度出发,着重关注电力网络的全局状态,综合考虑电力网络中各节点之间的连通能力,以及网络中节点的数目N,通过观察输电线路断开前后电力网络凝聚度的变化量,来衡量电力网络中各输电线路的重要程度。
1 基于网络凝聚度的线路重要度评价方法
网络的凝聚度取决于两个因素:一个是网络中各节点间的连通能力,另外一个是网络中的节点数目N。节点间的连通能力可以用网络的平均距离L来衡量,即所有节点对之间距离的平均值。例如在人际关系网络中,若人与人之间的交流越方便(L越小),网络中的人数越少(N越小),则该网络的凝聚度就越高。网络的凝聚度定义为,网络中节点总数N与平均距离L乘积的倒数,可以表述为

(1)
其中,N≥2,dij为节点i到节点j的最短距离,即节点i到节点j边数最少的路径包含的边的条数。当网络中只有一个节点时,令Φ=1。由表达式(1)可知,0<Φ≤1。
根据网络凝聚度的定义,本文提出了基于网络凝聚度的线路重要度评价方法,将输电线路的重要性表示为
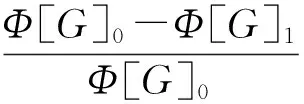
(2)
其中,IMC(vi,vj)为连接节点i和节点j的线路的重要度,Φ[G]0为线路断开前网络的凝聚度,Φ[G]1为线路断开后最大连通子网的凝聚度。相同条件下,线路断开后,IMC越大,意味着剩余最大连通子网的平均距离L越大,剩余子网节点间平均距离越大,网络越难通信和进行能量传输,因此断开的连边越重要。
2 基于本文方法的线路重要度计算
为了方便后续的研究工作,对IEEE14节点、IEEE57节点标准测试网络中各输电线路进行编号,并通过PAJEK软件绘制出这两个节点系统的拓扑结构简化图,如图1、图2所示。
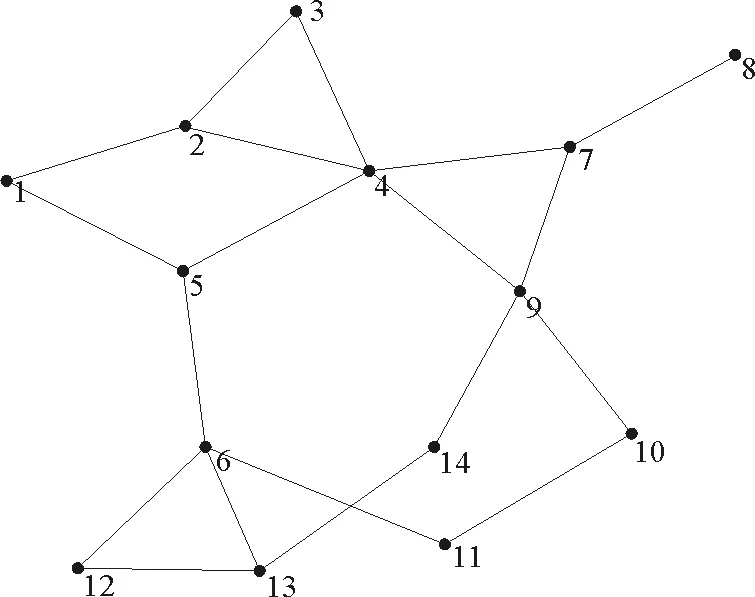
图1 IEEE14节点系统拓扑结构简化图
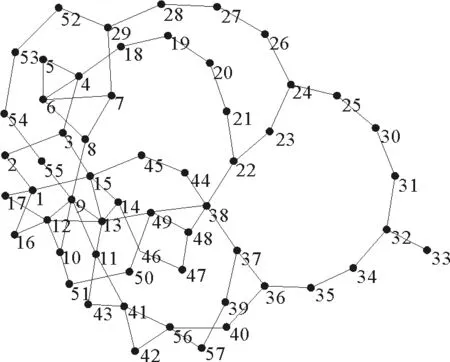
图2 IEEE57节点系统拓扑结构简化图
按照本文提出的关键线路评价的方法,计算出了IEEE14节点、IEEE57节点标准测试网络中各线路的重要度,如图3所示。

图3 线路重要度
3 线路识别效果对比
为了验证本文提出的关键线路识别方法的可行性和有效性,将本文方法的实验结果与文献[19]中提出的方法的实验结果进行对比。其中,文献[19]将节点间距离的倒数和的平均值定义为网络的全局效率,认为相同情况下,线路断开前后网络的全局效率变化得越大,则断开的线路在网络中越重要。表1、2分别给出了IEEE14节点、IEEE57节点标准测试网络中,两种算法确定的线路重要性计算排序的部分结果。

表1 IEEE14网络中两种算法的对比
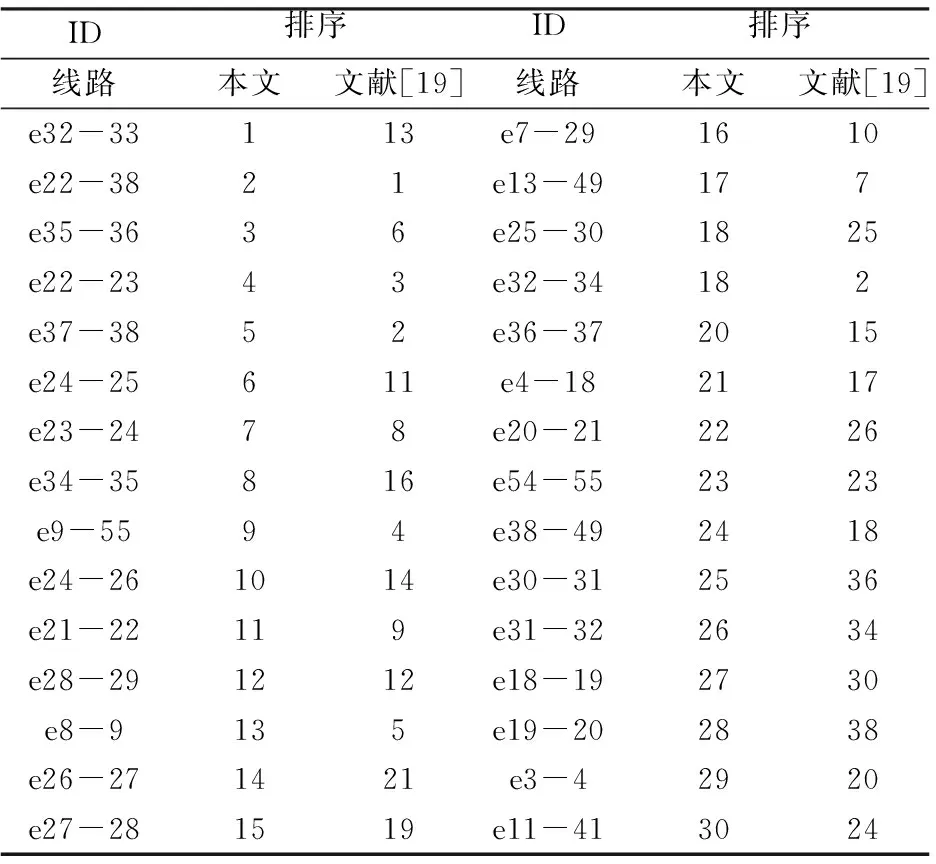
表2 IEEE57网络中两种算法的对比
从表1中可以看出,线路e7-8和线路e5-6都为网络中的重要线路,对比两条线路在IEEE14节点标准测试网络的拓扑结构图中的位置,发现线路e7-8在网络中承担着更为重要的枢纽作用,线路e7-8的失效会使得8号发电机节点与网络分离,发电机的功率无法送出,因此该线路在网络中更为关键。经过进一步的对比分析,还发现对于IEEE14节点标准测试网络,在两种评价方案下,除极个别线路的重要度排序不同外,其他线路的排序相一致,这说明了本文提出的关键线路的衡量方法是合理且可行的。
表2是利用本文方法计算得出的IEEE57节点标准测试网络中排在前30位的重要线路与文献[19]的计算结果对比表。由此表可以看出本文计算排在前30位的重要线路除了e30-31、e31-32和e19-20这3条连边外,其余连边在文献[19]中也是排在前30位的,只是这些连边的重要度排序有所不同。分析IEEE57节点标准测试网络的拓扑结构简化图,可以得知,本文排第一的线路e32-33是负荷节点33接入网络中的唯一途径,其承担着为负荷节点33传输电能,保证节点33正常工作的重要任务,一旦其发生故障,负荷节点33将与网络脱离无法正常工作。文献[19]中排第一的线路是e22-38,该线路断开后,整个网络仍然是连通的,不会发生网络的断裂,通过调整功率的分配,所有节点仍可正常工作。因此,线路e32-33比线路e22-38更重要,本文方法对最重要线路的检测更准确。接下来将从结构和动力学角度对本文其他线路的重要性进行验证。
4 基于结构和动力学的识别效果验证
在上一节中,可以看到对于IEEE14节点标准测试网络,本文关键线路辨识方法与文献[19]中方法的排序结果基本一致,而对于IEEE57节点标准测试网络,两种方法之间有一定的差别,为了进一步说明本文提出的关键线路算法的合理性,本节将对IEEE57节点标准测试网络,从拓扑结构和动力学角度来进行验证分析。
首先,从电力网络的拓扑结构出发,对本文提出的基于网络凝聚度的线路重要度评价方法的合理性进行验证。移除线路后,网络裂解出的独立社区越多,则网络受到的破坏程度越大,网络的脆弱程度也越高,由此也说明了相应的被移除线路在网络中越重要。根据线路的重要度排序结果,移除IEEE57节点标准测试网络中前30条重要线路,观察网络拓扑结构的变化情况。图4、图5给出了分别采用本文方法与文献[19]中方法所得的实验结果。
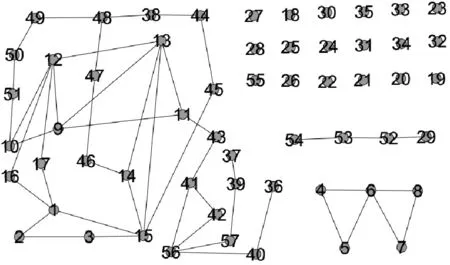
图4 本文算法删除前30条线路后的图形
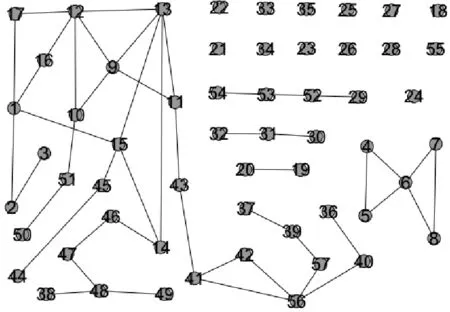
图5 文献[19]中算法删除前30条线路后的图形
图4为按照本文算法删除前30条重要线路后形成的拓扑图形,从图中可以看出,前30条重要线路删除后,IEEE57节点标准测试网络被划分为21个独立的社区,说明该方法有效地计算出了IEEE57节点标准测试网络中的关键线路。图5给出了文献[19]中算法得到的计算结果排序后,删除前30条重要线路所得的图形,图中仅将网络划分为18个独立的社区。对比图4和图5,可以得到,删除前30条重要线路后,两种方法得到的最大连通子网的节点数均为30个,同时,按照本文算法删除前30条重要线路后,形成的独立社区比文献[19]中算法所得的独立社区多3个,说明按照本文算法对网络进行攻击,给网络带来的破坏程度更大。因此,本文提出的关键线路的计算方法识别效果更好。
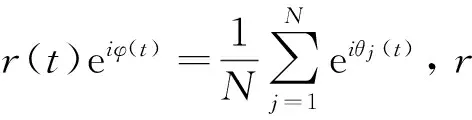
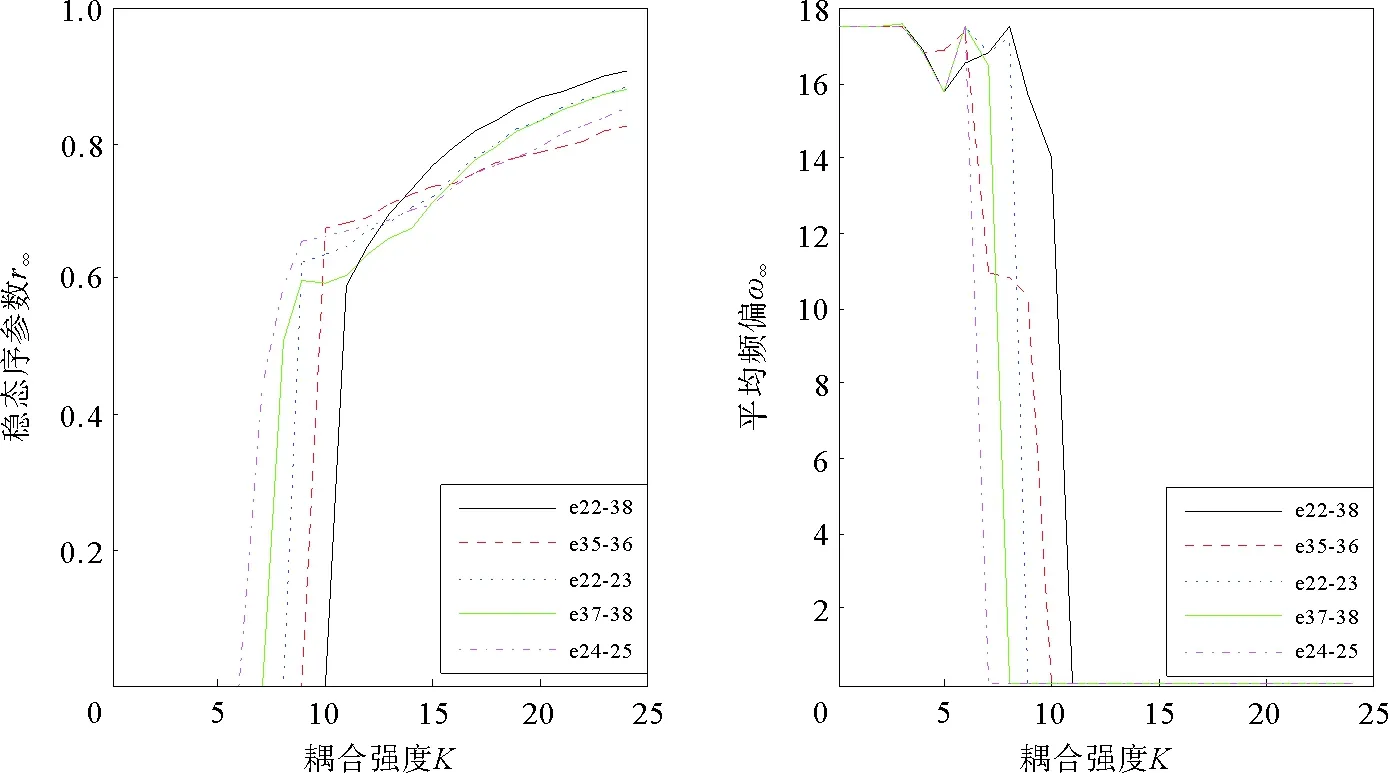
图6 移除线路后各剩余最大连通子系统稳态序参数、平均频偏与耦合强度的关系
从图6中的仿真结果,可以看到,随着耦合强度K的增大,系统的稳态序参数会逐渐增大,并接近于1,平均频偏会逐渐下降到0。平均频偏刚好下降到0时的耦合强度为系统的同步阈值。图中各曲线的同步阈值的大小依次为Kc黑>Kc红>Kc蓝>Kc绿>Kc紫,同步阈值越大,意味着线路移除后剩余系统的同步能力越差,因此断开的线路在系统中的地位也就越重要,据此得到线路重要度的排序结果为:e22-38>e35-36>e22-23>e37-38>e24-25,这与本文提出的基于网络凝聚度的线路重要度评价方法结果是一致的,因此从动力学角度对部分边的重要度排序也验证了本文方法的合理性,同时也说明文献[19]中得到的关键线路排序,从系统同步性能角度分析,并不完全合理。
5 结语
电力网络中关键线路的识别研究对电力网络的保护和改造具有一定的指导意义。本文从复杂网络理论角度,结合网络的凝聚度指标,提出了基于网络凝聚度的关键线路辨识方法,有效地定位出对系统稳定运行有着重要影响的关键线路。接着将本文方法与基于网络全局效率的方法进行对比分析,并进一步从拓扑结构和动力学角度进行仿真验证,结果表明本文提出的方法在识别网络的关键线路上更合理有效。在建立电力网络的拓扑结构模型时,我们只区分了发电机和负载两类节点,忽略了系统中的其他单元,这种建模方式使得最终的实验结果具有一定局限性,因此,建立更加符合实际的电力网络模型将是下一步研究工作中需要考虑的一个方面。
[1]Pagani G A, Marco A. From the grid to the smart grid, topologically[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 449: 160-175.
[2]Bhangu N S, Singh R, Pahuja G L. Reliability centred maintenance in a thermal power plant: a case study[J]. International Journal of Productivity and Quality Management, 2011, 7(2): 209-228.
[3]Park J W, Seol W C. Considerations for severe accident management under extended station blackout conditions in nuclear power plants[J]. Progress in Nuclear Energy, 2016, 88: 245-256.
[4]Aguiar A S, Lamego Simoes Filho F F, Alvim A C M, et al. Station Blackout in unit 1 and analysis of the wind field in the region of Angra dos Reis[J]. Annals of Nuclear Energy, 2015, 78: 93-103.
[5]Watanabe T, Ishigaki M, Hirano M. Analysis of BWR long-term station blackout accident using TRAC-BF1[J]. Annals of Nuclear Energy 2012, 49: 223-226.
[6]陈增强, 谢征, 张青. 基于非负矩阵分解的复杂网络重构[J]. 复杂系统与复杂性科学, 2016, 13(3): 26-32.
Chen Zengqiang, Xie Zheng, Zhang Qing. Complex network reconstruction based on non negative matrix factorization[J]. Complex Systems and Complexity Science, 2016, 13(3): 26-32.
[7]张欣. 多层复杂网络理论研究进展:概念、理论和数据[J]. 复杂系统与复杂性科学, 2015, 12(2): 103-107.
Zhang Xin. Research progress of multi layer complex network theory: concept, theory and data[J]. Complex Systems and Complexity Science, 2015, 12(2): 103-107.
[8]巩长忠, 李飞燕. 不确定复杂网络的广义矩阵投影同步[J]. 复杂系统与复杂性科学, 2015, 12(3): 53-60.
Gong Changzhong, Li Feiyan. Generalized matrix projective synchronization of uncertain complex networks[J]. Complex Systems and Comple-xity Science, 2015, 12(3): 53-60.
[9]王海峰, 李旺, 顾国彪,等. 风力发电机自循环蒸发内冷系统稳定性的研究[J]. 物理学报, 2016, 65(3): 38-45.
Wang Haifeng, Li Wang, Gu Guobiao, et al. Study on the stability of self circulation evaporative cooling system of wind turbine[J]. Physical Science Journal, 2016, 65(3): 38-45.
[10] 杜江, 郭瑞鹏, 李传栋,等. 电力系统可靠性评估中的重要控制法[J]. 电力系统自动化, 2015, 39(5): 69-74.
Du Jiang, Guo Ruipeng, Li Chuandong, et al. Important control method in reliability evaluation of power system[J]. Automation of Electric Power System, 2015, 39(5): 69-74.
[11] 丁明, 韩平平. 加权拓扑模型下的小世界电网脆弱性评估[J]. 中国电机工程学报, 2008, 28(10): 20-25.
Ding Ming, Hang Pingping. Vulnerability assessment of small world power grid with weighted topological model[J]. Chinese Journal of Electrical Engineering, 2008, 28(10): 20-25.
[12] 王涛, 高成彬, 顾雪平,等. 基于功率介数的电网关键环节辨识[J]. 电网技术, 2014, 38(7): 1907-1913.
Wang Tao, Gao Chengbin, Gu Xueping, et al. Identification of key link in power system based on power dielectric[J]. Power System Technology, 2014, 38(7): 1907-1913.
[13] 魏震波, 刘俊勇, 朱国俊,等. 基于电网状态与结构的综合脆弱性评估模型[J]. 电力系统自动化, 2009, 33(8), 11-14.
Wei Zhenbo, Liu Junyong, Zhu Guojun, et al. Integrated vulnerability assessment model based on state and structure of power network[J]. Automation of Electric Power System, 2009, 33(8), 11-14.
[14] Karimi E, Ebrahimi A. Considering risk of cascading line outages in transmission expansion planning by benefit/cost analysis[J]. International Journal of Electrical Power and Energy Systems, 2016, 78: 480-488.
[15] Ou Y M, Zhao L J, Pan Z Z, et al. Comparisons of complex network based models and direct current power flow model to analyze power grid vulnerability under intentional attacks[J]. Physica A: Statistical Mechanics and Its Applications, 2014, 430: 45-53.
[16] Ou Y M, Pan Z Z, Hong L, et al. Correlation analysis of different vulnerability metrics on power grids[J]. Physica A: Statistical Mechanics and Its Applications, 2014, 396: 204-211.
[17] 张富超, 谢成荣, 沈立新,等. 基于源流路径链和输电介数的电网关键线路辨识[J]. 电力系统保护与控制, 2015, 43(21): 7-12.
Zhang Fuchao, Xie Chengrong, Shen Lixin, et al. Identification of key lines in power system based on source and path chain and transmission medium number[J]. Power System Protection and Control, 2015, 43(21): 7-12.
[18] 鞠文云, 李银红. 基于最大流传输贡献度的电力网络关键线路和节点辨识[J]. 电力系统自动化, 2012, 36(9): 6-12.
Ju Wenyun, Li Yinhong. The key lines and nodes identification of power network based on the maximum transmission contribution degree[J]. Automation of Electric Power System, 2012, 36(9): 6-12.
[19] Crucitti P, Latora V, Marchiori M. Locating critical lines in high-voltage electrical power grids[J]. Fluctuation and Noise Letters, 2005, 5(2): 201-208.
[20] Rohden M, Sorge A, Timme M, et al. Self-organized synchronization in decentralized power grids[J]. Physical Review Letters, 2012, 109(6): 064101.
TheCriticalLinesIdentificationofthePowerGridsBasedontheComplexNetworkTheory
FU Jie, ZOU Yanli, XIE Rong
(College of Electronic Engineering, Guangxi Normal University, Guilin 541004, China)
Based on the complex network theory, this paper proposes a critical lines evaluation method for power network according to the cohesion degree of network. This method focuses on the overall state of the power network, the connectivity between nodes in the power network and the numbers of nodes in the network. It can measure the importance of each transmission line in power network by observing the change of cohesion degree of power network before and after transmission line breaking. Because of the comparison between the calculation results of this paper and the results of the existing critical lines evaluation schemes based on the network performance in the literature, the simulation on the topological structure and dynamics, the reasonable and effective of the method is proved.
complex network; degree of aggregation; power grids; critical lines identification; topological structure; dynamics
1672-3813(2017)03-0091-06;
10.13306/j.1672-3813.2017.03.009
TM711
A
2016-12-04;
2017-08-29
国家自然科学基金(11562003);广西多源信息挖掘与安全重点实验室系统性研究课题基金(13-A-02-03);广西研究生教育创新计划项目(YCSZ2014098)
傅杰(1991-),男,湖南岳阳人,硕士研究生,主研方向为复杂网络理论及其应用。
邹艳丽(1972-),女,博士,教授,主要研究方向为非线性电路系统的混沌控制与同步、复杂网络的控制与同步。
(责任编辑李进)
