基于节点相似性的LFM社团发现算法

2017-12-19杨晓波陈楚湘王至婉

复杂系统与复杂性科学 2017年3期

关键词：相似性社团精度

杨晓波，陈楚湘，王至婉

(1.信息工程大学理学院理学院，郑州 450000；2.河南中医学院第一附属医院呼吸科，郑州 450000)

基于节点相似性的LFM社团发现算法

杨晓波1，陈楚湘1，王至婉2

(1.信息工程大学理学院理学院，郑州 450000；2.河南中医学院第一附属医院呼吸科，郑州 450000)

传统的局部适应度社团发现算法(LFM)在社团结构模糊的网络中精度下降严重。针对此问题，提出LFMJ算法。利用邻居节点信息和改进的杰卡德系数重构网络，使网络结构更为清楚，社团划分结果更为准确。为验证算法，选择了5种算法在LFR网络和真实网络中进行测试，包括LFMJ、LFM和传统的LPA算法以及性能较好的WT和FUA算法。结果表明：在标准LFR网络中，LFMJ精度高于LFM和LPA，与FUA和WT相当；在真实网络和具有重叠结构的LFR网络中，LFMJ精度优于其他4种算法。

复杂网络；社团发现；节点相似性；杰卡德系数

0 引言

复杂网络用节点表示系统元素，用边表示元素关系，将复杂系统表示成网络模型，探索系统内在规律。社团结构是复杂网络的重要属性之一，分析社团结构，可以发现隐藏在网络表象下的社团实质规律[1]。从Newman学者提出GN算法以来，社团发现越来越受到学者的关注。众多不同的算法相继被提出。

最早的社团发现算法是Newman基于边介数提出的GN算法[2]，通过不断删除介数最大的边来划分社团。该算法每次都需要计算边介数和模块度，时间复杂度很高，不适用于大型网络。2006年Newman又基于谱聚类提出谱平分算法(Spectral Bisection Method)[3]。该算法将网络节点映射到特征向量空间，通过谱聚类算法对节点进行聚类，完成社团划分过程。在社团结构不明显的网络中，该算法精度较低，而且特征向量的计算开销较大。Raghavan等提出了基于传播标签的算法(Label Propagation, LPA)[4]，该算法具有线性的时间复杂度O(m)，极少次就能收敛，但算法结果不稳定。P. Pons和M. Latapy提出了基于随机游走社团划分方法(Walk Trap, WT)[5]，该算法具有较好的时间复杂度而且社团划分精度较高。Blondel等人提出了基于模块度优化的快速模块性优化算法(Fast Unfolding Algorithm, FUA)[6]。该算法具有较高的社团划分质量，被Fortunato等人认为是目前性能最佳的模块性优化算法[7]。

随着研究的深入，人们发现一个节点可同时属于多个社团，这种重叠的社团结构更符合实际情况。Lancichinetti等人提出LFM算法[8]用于发现重叠社团。该方法以具有某种特征的子网络为种子，通过合并、扩展等操作向邻接节点扩展，直至获得评价函数最大的社团。算法最坏情况下的时间复杂度为O(n2)。

LFM算法是一种基于局部信息的社团划分方法，无需获得网络全局信息，收敛速度较快，而且可用于赋权网络，具有较广的适用范围。但存在以下问题：

1)由于LFM算法种子节点的选取是随机的，可能导致不稳定的结果[9]，稳定性较差；

2)由于基于不完整的局部信息，该算法的社团划分精度在社团结构不明显的网络中会受到较大影响。

为提高LFM算法精度与稳定性，提出LFMJ(LFM Based on Jaccard)算法。该算法通过节点度选择种子节点，基于改进的Jaccard系数衡量节点相似性，用邻居节点包含的信息来弥补不完整的局部信息，使网络结构更为清晰，社团划分结果更为准确。

1 LFM算法简介

该算法首先对社团定义了适应度函数fG，用于表示社团内外部关系。函数fG定义为

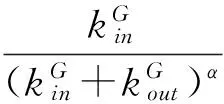
(1)

(2)

根据定义的适应度函数，LFM算法随机选取种子节点作为初始社团，并计算当前社团适应度函数。然后计算邻居节点对社团的适应度，并以此为依据决定是否将节点加入社团，对社团进行扩张。如此迭代，直至遍历所有节点，完成社团划分。

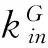
2 LFMJ算法

传统LFM算法效果不稳定，在混合程度较高的网络中精度下降严重，原因在于种子节点的随机选择，和不完整的局部信息。

网络节点对网络中其他节点也有直接或间接的影响力[10]。网络节点的邻居节点经常包含隐藏信息，一定程度上反映了节点的社团属性，但在传统LFM算法中未能得到充分利用。LFMJ算法，首先通过节点度选择种子节点，然后运用改进的Jaccard系数衡量节点相似性，用邻居节点包含的信息完善不完整的局部信息，使社团划分精度得到提高。

2.1 Jaccard相似系数

Jaccard系数常用于计算两个样本的相似度。定义为两个集合A和B交集元素的个数在并集中所占的比例：

(3)

社团本质上是一种社会学概念，具有社会属性。在现实社会网络中，属于同一社团的人经常具有相同或相似的社交圈。如果两个节点拥有较多的共同邻居节点，则认为它们的相似度较大，属于同一社团的可能性较大[11]。如图1所示。

对于节点a和b，节点a的邻居节点构成集合A，节点b的邻居节点构成集合B。两节点的邻居节点完全重合A=B，有理由认为两节点有极大概率属于同一社团。

2.2 基于Jaccard系数衡量节点相似度

传统Jaccard系数可以衡量节点i，j的相似性，公式定义为

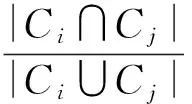
(4)

Ci和Cj为节点i，j的邻居节点集合。

实践中发现，公式(3)存在一定问题，即节点i拥有较大节点度时，会使分母|Ci∪Cj|较大，导致节点度较高的节点与其他节点相似度较小。而网络中节点度经常服从幂律分布，即少数节点具有很高的节点度。这些少数节点通常是网络核心，较小的节点相似度明显不符合实际情况。如图2所示。

图2中节点v和节点i，j公共邻居节点均为节点0，仅因为节点i本身更高的节点度，降低了节点v和i的相似度，显然不符合实际。因此，将分母设定为较小集合包含的节点数，即：

(5)

这样的改进仍然存在问题，如果两节点没有共同邻居节点，但节点间有一条边，此时相似性系数为0，不能合理表示节点关系。如图3所示。

图1 邻居节点示例Fig.1 Example of neighbor nodes

图2 节点相似度示例Fig.2 Example of vertex similarity

图3 存在连接的节点相似度Fig.3 Vertex similarity of two nodes with edge

图中节点i和j的邻居节点交集为空集，按照Jaccard系数计算相似度为0，与实际情况不符。因此，再一次调整，使节点邻居集合包括自身，只要两节点之间有边，集合Ci与Cj之间至少有一个交集，避免相似性系数为0，即：

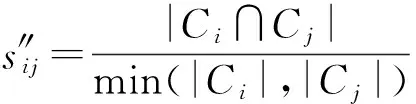
(6)

2.3 划分社团结构

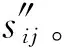
(7)

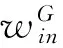
(8)

图4 算法流程Fig.4 Algorithm flowchart

运用LFM算法进行社团结构划分。算法流程如图4所示。

1)网络结构预处理，计算节点间相似度矩阵S；

2)将所有节点加入种子节点队列Q，计算各节点的节点度ki；

6)判断队列Q是否为空，若不为空，则继续进行步骤3；若为空则算法结束。

2.4 时间复杂度分析

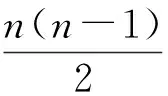
3 实验结果与分析

为了验证算法有效性，将LFMJ算法与传统的LFM算法和LPA算法以及目前性能较好的FUA算法、WT算法进行比较，在LFR人工网络和真实网络中进行测试。

3.1 数据集

采用人工网络和真实网络两种数据集对算法进行测试。

3.1.1 LFR人工网络

人工网络采用经典的LFR基准网络[12]，该网络于2008年由Lancichinetti等人提出，参数含义见表1。

表1 参数含义Tab.1 Meaning of parameters

按照文献[13]设置LFR网络参数[13]如下：网络规模N设置为1 000；平均节点度k设置为20，最大节点度max_k设置为50；节点度和社团规模幂律分布参数分别设置为ε1=-2，ε2=-1。设置两组不同的社团规模参数以生成两个网络S1和S2：min_c=10，max_c=50；min_c=20，max_c=100。参数设置见表2：

混合参数u从0变化到0.7，间隔为0.1，测试不同混合程度下算法的社团划分效果。

为了检验重叠社团结构，Lancichinetti等人于2009年对其进行改进，加入重叠参数on和om，使之具有重叠社团结构。见表3。

3.1.2 真实网络

真实网络采用社团结构已知的经典数据集：空手道网络(Zachary's karate club)，美国大学生足球网络(American College football)和美国政治书籍网络(Books about US politics)。

表2 LFR参数设置Tab.2 Parameter settings of LFR

空手道网络由美国一所大学空手道俱乐部成员关系得到，包含34个节点和78条边，分为两个社团。美国大学足球网络包含115个节点，616条边，12个社团。美国政治书籍网络是由V. Krebs从Amazon销售的美国政治相关书籍数据上建立的网络，包含105个节点，441条边，3个社团。

表3 重叠社团网络参数Tab.3 Parameters of LFR with overlapping community structure

图5 网络测试结果Fig.5 Test results in networks

图6 重叠网络测试结果Fig.6 Test results in network with overlapping community structure

3.2 评价指标

采用Lancichinetti提出的扩展的规范化互信息(Extended Normalized Mutual Information, ENMI)来衡量和比较重叠社团算法的精度[8]。假设已知社团结果为集合C′，算法发现的社团结果为集合C″，ENMI衡量的是两者之间的一致性，ENMI越大说明算法精度越高。

3.3 结果与分析

LFM算法社团规模参数α取值一般在0.5～1.5之间，实践中常取0.8、1.0或1.2，这里设置参数α为1.2，LFMJ算法取同样的α值。WT算法步长参数一般设置在3～5之间，这里设置步长为4。

3.3.1 LFR人工网络

根据LFR参数设置，生成S1和S2两个网络，在0～0.7之间调整社团混合参数u，计算不同混合程度网络下算法的ENMI值。测试结果如图5所示。

在社团规模较小的S1网络中，LFMJ算法精度优于传统的LFM算法，而且优于LPA和FUA算法，与WT算法精度相当；在社团规模较大的S2网络中，LFMJ算法同样优于传统LFM算法和LPA算法，与WT和FUA算法相当。

相比于性能较好的WT和FUA算法，LFMJ算法具有发现重叠社团结构的优势。根据表2参数设置，设置u=0.3，om=5，在节点数为1 000的网络中设置重叠节点数on从0到500变化，计算各算法的ENMI值，结果如图6所示。

在具有重叠社团结构的网络中，随着重叠节点数增加，各类算法社团划分精度逐渐下降，其中LFMJ算法下降最为缓慢，算法精度优于其他算法。

由上述可知，相比于传统LFM和LPA算法，算法LFMJ具有更高的精度；相比于性能较好的WT和FUA算法，LFMJ算法在重叠网络中具有明显的优势，证明了算法的有效性。

3.3.2 真实网络

真实网络采用空手道网络，美国大学生足球网络和美国政治书籍网络。算法的ENMI值结果见表4。

3个网络中，LFMJ算法均取得了更高的ENMI值，即LFMJ算法在真实网络中具有更高的精度。

表4 真实网络ENMITab.4 ENMI of real networks

4 结束语

在传统LFM算法的基础上，LFMJ算法通过节点度选择种子节点，解决了传统LFM算法的稳定性问题；利用邻居节点和改进的Jaccard系数衡量节点相似性，并重构网络，进行社团结构划分，取得了更高的精度，改善了社团结构不明显网络中社团发现精度下降的问题。

算法在种子节点选择上还存在不足，节点度并不是选择种子节点的最佳标准。下一步将继续研究种子节点对社团划分精度的影响。

[1]高启航,景丽萍,于剑，等. 基于结构和适应度的社区发现[J]. 中国科学技术大学学报, 2014, 44(7): 563-569.

Gao Qihang, Jing Liping, Yu Jian, et al. Community detection based on structure and fitness [J]. Journal of University of Science and Techno-logy of China, 2014, 44(7): 563-569.

[2]Girvan M, Newman M E J. Community structure in social and biological networks [J]. P Natl Acad Sci USA, 2002, 99(12): 7821-7826.

[3]Newman M E J. Modularity and community structure in networks [J]. Proc of National Academy of Science, 2006, 103(23): 8577-8582.

[4]Raghavan U N, Albert R, Kumara S. Near linear-time algorithm to detect community structures in large-scale networks [J]. Phys Rev E, 2007, 76(3): 036106.

[5]Pascal P, Matthieu L. Computing communities in large networks using random walks [J]. J Graph Algorithms Appl, 2006, 10(2): 191-218.

[6]Blondel V D, Guillaume J L, Lambiotte R, et al. Fast Unfolding of communites in large networks [J]. Journal of Statistical Mechanics: Theory and Experiment, 2008, (10):155-168.

[7]刘大有,金弟,何东晓,等. 复杂网络社区挖掘综述[J]. 计算机研究与发展, 2013, 50(10): 2140-2154.

Liu Dayou, Jin Di, He Dongxiao, et al. Community mining in complex networks [J], Journal of Computer Research and Development, 2013, 50(10): 2140-2154.

[8]Lancichinetti A, Fortunato S, Kertesz J. Detecting the overlapping and hierarchical community structure in complex networks [J]. New Journal of Physics, 2009, 11(3): 033015.

[9]李建华,汪晓锋,吴鹏. 基于局部优化的社区发现方法研究现状[J]. 中国科学院院刊, 2015, 30(2): 238-247.

Li Jianhua, Wang Xiaofeng, Wu Peng. Review on community detection methods based on local optimization [J]. Bulletin of Chinese Academy of Sciences, 2015, 30(2): 238-247.

[10] 刘倩,刘群. 基于引力度扩展的重叠社区发现算法[J]. 计算机工程与设计, 2014, 35(3): 852-856.

Liu Qian, Liu Qun. Overlapping community detection algorithm based on expansion of gravitational degree [J]. Computer Engineering and Design, 2014, 35(3): 852-856.

[11] 张若昕,柴丹炜,熊小峰,等. 基于节点相似度的社团发现算法研究[J]. 电脑知识与技术, 2015, 11(8): 42-44.

Zhang Ruoxin, Chai Danwei, Xiong Xiaofeng, et al. The research on community detection algorithm based on node similarity [J]. Computer Knowledge and Techonlogy, 2015, 11(8): 42-44.

[12] Lancichinetti A, Fortunato S, Radicchi F. Benchmark graphs for testing community detection algorithms [J]. Phys Rev E, 2008, 78(4): 046110.

[13] Lancichinetti A, Fortunato S. Community detection algorithms: a comparative analysis [J]. Phys Rev E, 2009, 80(5): 056117.

LFMCommunityDetectionAlgorithmBasedonVertexSimilarity

YANG Xiaobo1, CHEN Chuxiang1, WANG Zhiwan2

(1.College of Science, The Information Engineering University, Zhengzhou 450000, China; 2.Respiratory Department, the First Affiliated Hospital of Henan University of Traditional Chinese Medicine, Zhengzhou 450000, China)

In network with fuzzy community structure, precision of the traditional LFM algorithm decreases apparently. In order to solve this problem, an LFMJ algorithm is presented. Using the information of neighbor nodes and improved Jaccard coefficient, this algorithm reconstructed the network structure, and improved the precision of community division results. To validate the algorithm, five algorithms was tested in LFR benchmark and real networks, including LFMJ, traditional LFM, LPA algorithm and WT, FUA algorithm, which have better performance in community detection. The results show that, in LFR network, the accuracy of LFMJ is higher than both LFM and LPA, equaling to WT and FUA algorithm. In real network and LFR network with overlapping community, LFMJ gets the highest accuracy than others. The effectiveness of the algorithm is proved.

complex network; community detection; vertex similarity; Jaccard coefficient

1672-3813(2017)03-0085-06；

10.13306/j.1672-3813.2017.03.008