基于混合蛙跳算法的PID控制器参数整定

赵转哲，何 康，何慧娟

(1.安徽工程大学 机械与汽车工程学院,安徽 芜湖 241000;2.宿州学院 机电学院,安徽 宿州 234000)

基于混合蛙跳算法的PID控制器参数整定

赵转哲1，何 康2，何慧娟1

(1.安徽工程大学 机械与汽车工程学院,安徽 芜湖 241000;2.宿州学院 机电学院,安徽 宿州 234000)

PID控制在现代工业过程控制中应用广泛，但传统的 PID 参数整定方法已经不能完全适应现代工业的发展。利用一种新型的元启发式搜索的群智能算法——混合蛙跳算法对其3个参数进行优化设计，结合Simulink模型，进行基于MATLAB的离线仿真实验。结果表明，与粒子群算法相比，混合蛙跳算法的求解结果更加精确和稳定。

混合蛙跳算法；PID 控制；MATLAB 仿真；参数整定

比例-微分-积分(Proportional-Integral-Derivative, PID)控制器具有形式简单、鲁棒性好以及可靠性高等优点，成为目前主要的工业控制技术之一，已在机电、冶金、机械、化工等工业生产中得到广泛应用。而PID控制技术中一个至关重要的问题是控制器的参数整定问题，直接影响到系统的控制质量和控制器的鲁棒性[1]。早期的PID 参数整定一般是依靠经验丰富的工程技术人员反复凑试，费时耗力，再加上系统本身的非线性、时变性等问题，此法往往难以得到令人满意的结果。1942年，由Ziegler和Nichols 提出的Z-N经验公式法[2]，用于手工计算和设置控制器初值，至今还在工业控制中应用，但该方法获得的参数在有负载扰动时存在较大误差。随着计算机技术和人工智能理论的发展，新的参数整定方法不断涌现，如专家PID控制[3]、模糊PID控制[4-5]等，实现了参数的自整定，但因为其规则复杂，操作不便，其应用受到了一定的限制；同时，群智能算法如遗传算法[6]、粒子群算法[7]、蚁群算法[8]等被不断地应用于PID参数的整定过程，与专家系统等人工智能相比，具有操作方便、速度快的优点，不需要复杂的规则，便可以达到参数的最优设计，引起了广大学者的重视。

混合蛙跳算法(Shuffled Frog Leaping Algorithm, SFLA)是一种新颖的启发式生物群智能算法[9]，具有高效的计算性能和优良的全局搜索能力，目前，已经从最初的水资源网络中的管径优化转移到其它工程领域的优化问题[10-12]。本文采用SFLA进行PID参数整定和优化，并在MATLAB环境下实现该方法，通过实例仿真表明该方法的有效性，为进一步扩大PID控制在工业控制中的应用打下坚实的基础。

1 混合蛙跳算法原理

基本思想：在一片湿地中生活着一群青蛙，湿地内分布着许多离散的石头，青蛙通过寻找不同的石头进行反复跳跃，从而去找到食物较多的地方。该算法将蛙群分成多个子群，每个子群内青蛙借鉴粒子群优化算法的方法进行局部搜索，性能最差青蛙以一定的步长进行更新；而整个族群借鉴模因进化算法的方法，周期性地进行混合和重新分组，进行全局信息交流，从而使信息在全局与个体间进行交换，以便更好地寻优。这种深度局部搜索和全局信息交换的策略能够保证算法更大程度地落入局部最优值，而向全局最优靠拢[9-10]。

SFLA的基本步骤可以描述为：

1)全局搜索。

初始化：选择种群内青蛙个数F，子种群个数m，子群内青蛙个数n。指定全局最大进化代数Gmax，子群内部最大进化代数Lmax。

①在搜索空间随机初始化所有F个青蛙；

②计算每个青蛙的适应度函数；

③根据适应度对所有青蛙进行排序，得到全局最优青蛙Pg；

④将所有青蛙分成m个群，每个群包括n个青蛙。第1个青蛙分入第1个子群，第2个分入第2个子群，…，第m个分入第m个子群，第m+1个青蛙又分入第1个子群，以此类推；

⑤每个子群中执行子群内的局部搜索；

⑥重新混合所有青蛙；

⑦如果没有达到停止的条件，转到第②步。

2)子群内的局部搜索。

①在每个子群中确定最优青蛙Pb、最差青蛙Pw；

②对最差青蛙Pw进行更新(进化)。该青蛙的更新公式为

(1)

Pw_new=Pw+S.

(2)

式中：min( )和max( )分别是取最小值和最大值函数，rand为0～1的随机数，Smax为允许青蛙跳跃的最大步长。

③如果上一步产生一个更好的青蛙，则用它代替最差青蛙。否则，进行下一步；

④用全局最优Pg替换式(1)中Pb，如果找到一个更好的青蛙，则用它代替最差青蛙；如果还是不能找到性能更好的青蛙，则随机产生一个青蛙代替最差青蛙；

⑤按照预定的次数重复该过程。

2 PID参数整定的混合蛙跳算法实现

2.1PID参数

PID控制器是一种线性调节器，其原理如图1所示，它根据给定值r(t)和实际输出值c(t)构成偏差

e(t)=r(t)-c(t).

(3)

则偏差信号e(t)分别经过比例、积分、微分3个运算，并将三者作用和u(t)作为控制器的输出送入被控对象，PID控制器的控制规律为

(4)

写成传递函数的形式为

可以进一步记为

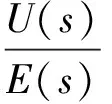
(5)

式中：Kp为比例系数，Ti为积分时间，Ki=Kp/Ti为积分常数，Td为微分时间，Kd=Kp/Td为微分常数。

PID参数整定即是确定最佳比例系数Kp、积分时间Ti和微分时间Td，使控制系统某一性能指标达到最佳。

2.2 基于SFLA的PID参数整定

利用SFLA进行PID参数整定的关键步骤如下：

1)将PID控制器的3个参数看成三维空间的一个矢量解，对应SFLA中的每一个青蛙个体，根据经验确定三参数的取值范围，即SFLA中变量的取值范围，以及SFLA中算法基本参数的设置。

2)PID控制模型建立。根据控制对象的传递函数以及PID控制器的原理，在MATLAB的Simulink环境下建立该系统的模型；

3)适应度函数的选择。适应度评估是进行混合蛙跳算法优化搜索的依据，而衡量PID控制器参数整定好坏的指标亦有很多，例如过渡过程的个别品质参数[1]以及利用幅值裕度和相角裕度的自整定方法[13]，实际上，在对控制性能进行评价时，要所有的性能指标都达到最优，几乎是不可能的，因为各参数之间相互影响，其中一个达到最优，有可能会使另一个指标的性能降低，为了达到整个系统综合性能最优化，需要采用一些能体现综合性能的指标。本文为使控制系统的偏差迅速减少，同时又具有较快的响应速度、较小的超调量且有一定的振荡和足够的阻尼，特选择在控制领域应用最广泛的ITAE指标作为评价系统性能的综合指标[14]，以此作为SFLA的适应度函数，理论上，该指标越小，控制系统的性能越好。以此找出青蛙种群中的性能最优青蛙和最差青蛙，进行SFLA的迭代更新操作。

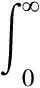
(6)

其过程如图2所示，由此可知：混合蛙跳算法与Simulink模型之间的桥梁是青蛙个体(即PID控制器参数组成的向量)和该青蛙所对应的适应度值(即控制系统的性能指标ITAE)。优化过程如下：SFLA产生青蛙群体，将每个青蛙以此赋值给PID控制器的参数Kp，Ki，Kd，然后运行控制系统的Simulink模型，得到该组参数对应的性能指标ITAE，再传递给SFLA中作为该青蛙的适应度值，最后判断是否可以退出SFLA，从而得到最优的整定参数。

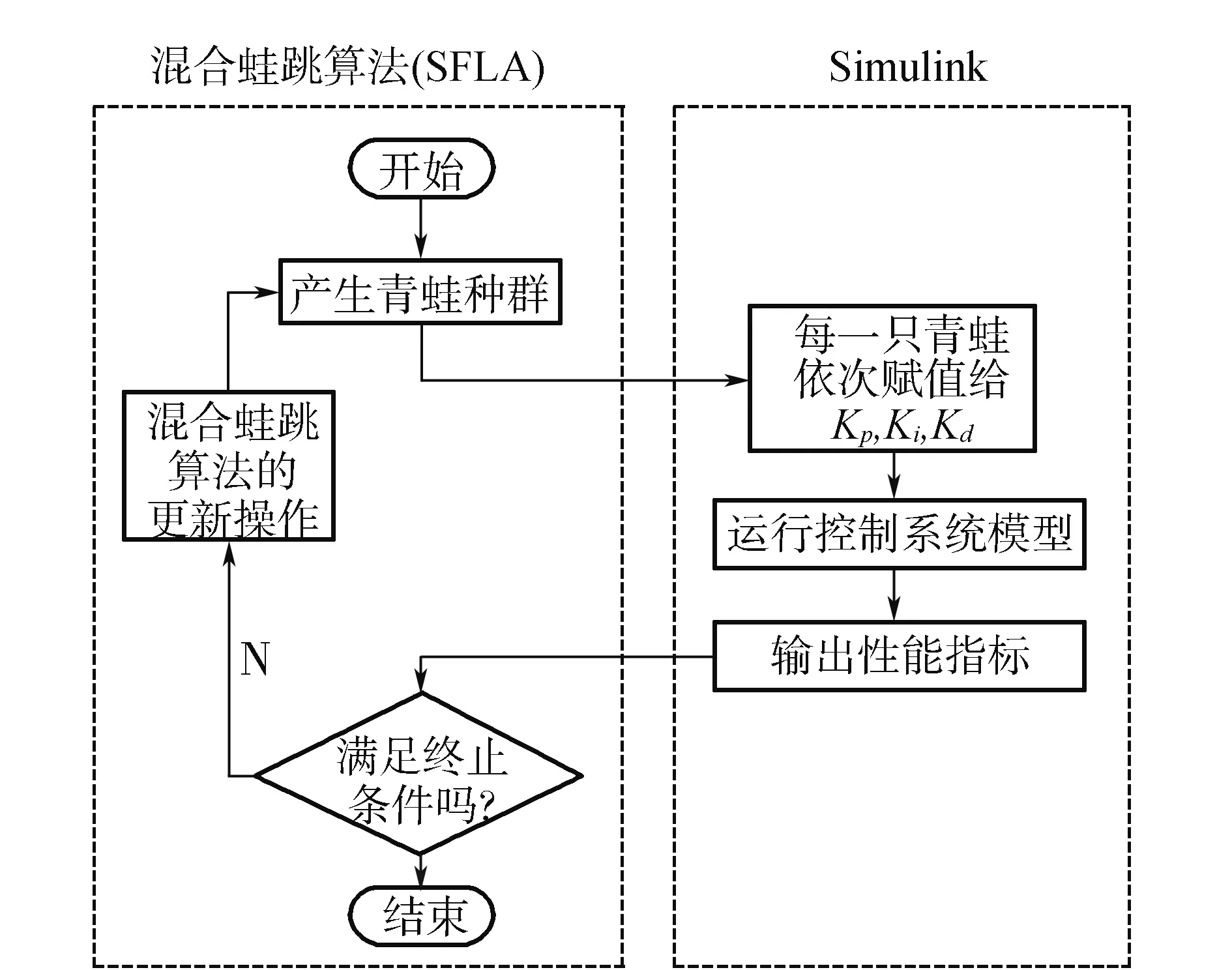
图2 SFLA优化PID的过程

3 仿真实例

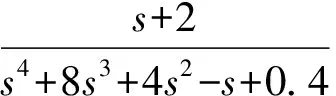
在MATLAB的Simulink环境下建立该系统的PID控制系统模型如图3所示[15]，其中，仿真时间为20 s，输出端子1的输出值即为性能指标ITAE。

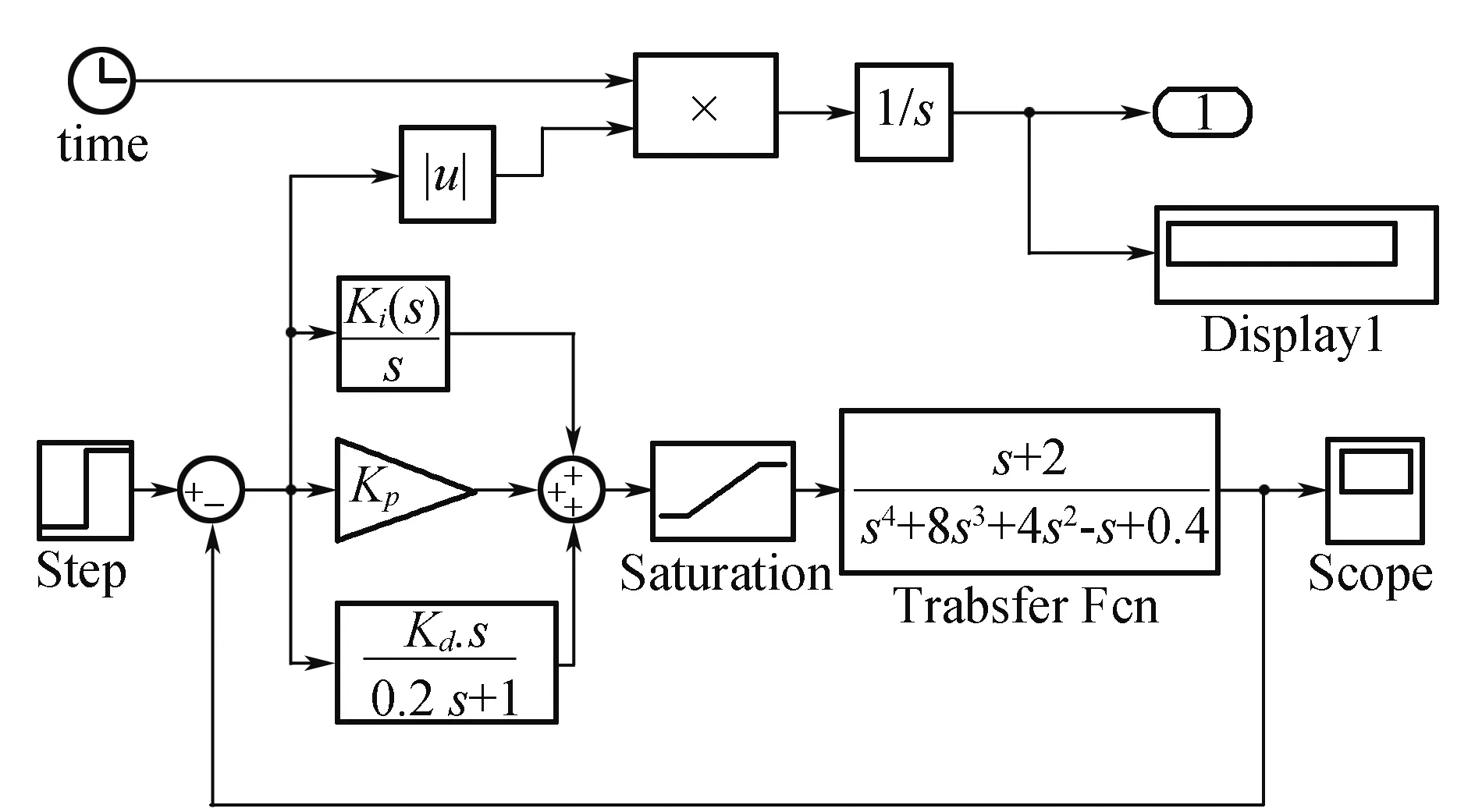
图3 Simulink环境下的PID控制系统模型

为了比较SFLA与其它群智能算法在优化PID参数时的优劣，根据文献[13]粒子群算法与遗传算法的参数设置情况，本文SFLA的算法参数设置：子种群数m=20，子群内青蛙个数n=5，因此，整个种群中青蛙的数量F=100，全体种群进行信息交换的进化次数Gmax=100，使得两种算法的群体规模和进化次数(或全局迭代次数)相同；另外，在SFLA中，允许最大步长Smax=3。每一种群的子群局部搜索进化次数Lmax=50。同时，PID控制器只有3个参数Kp，Ki，Kd需要待定，因此，适应度函数变量维数D=3，根据经验值，3个参数的取值范围为[0,300]，故在SFLA中变量的取值范围与此相同。

本质上，SFLA和PSO均属于随机搜索算法，为了全面分析并比较计算性能，本文将基于SFLA和PSO的PID参数整定模型独立运行20次，其结果如表1所示。

由表1可以看出，在相同的全局迭代次数下，基于SFLA算法的求解结果，无论是最优值、平均解，甚至于最差解，均优于PSO算法的结果，说明在PID的参数整定过程中，SFLA的求解精度高于PSO算法；另外，由两种算法求解结果的标准方差可知，对于该PID参数的整定模型，基于SFLA的求解结果的方差均小于PSO，说明SFLA算法的聚集性好，其稳定性要高于PSO，这个也可以从图4和图5看出。

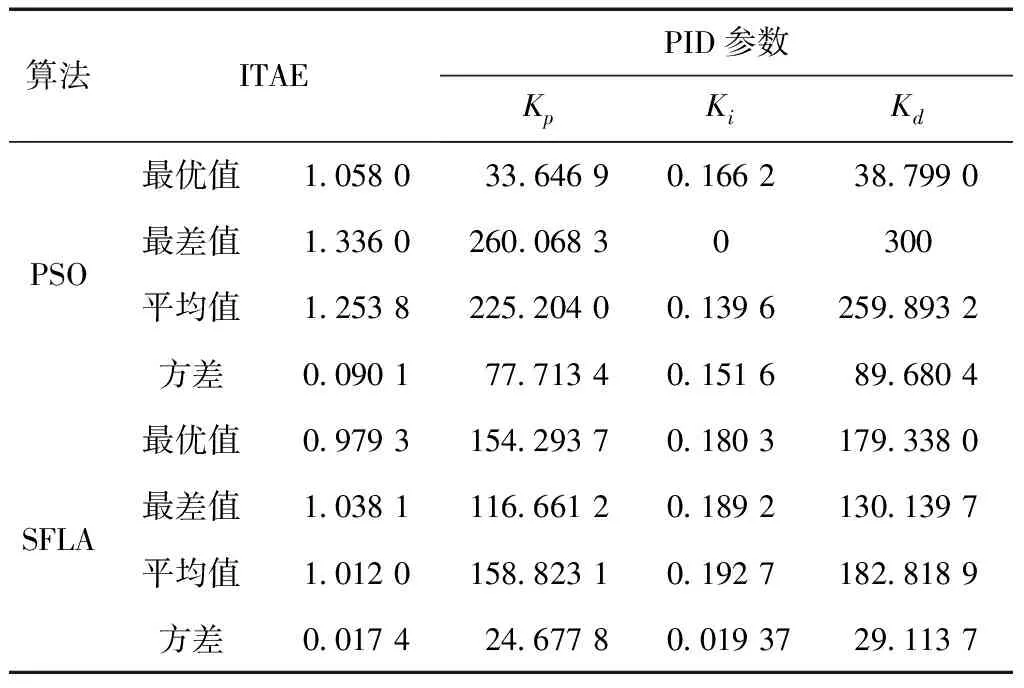
表1 基于SFLA和PSO求解得到的PID 3个最优参数及性能指标比较

两种智能算法在对该模型求解时，性能指标ITAE不断减少，说明两种算法均找到了PID参数，其收敛速度明显不一样，如图4和图5所示，对于SFLA，基本上在20步以内就达到了稳定值，即使是最差解，也是在30步左右稳定，且具有较好的精度；而PSO算法虽然也是在30步以内达到稳定，但因为其稳定时精度较差，导致结果不理想，有可能是算法陷入了局部最优而导致算法停滞。

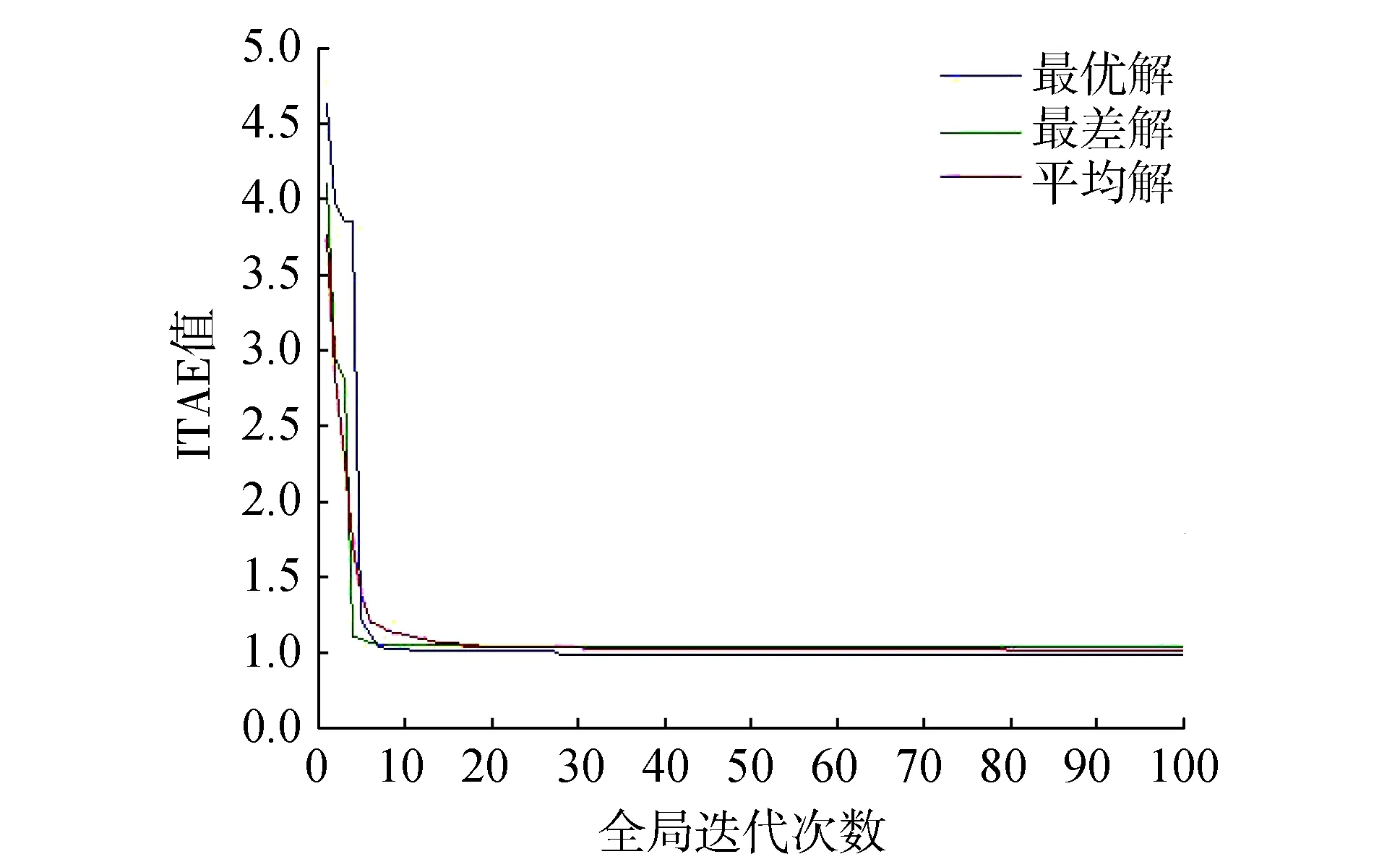
图4 基于SFLA求解的PID性能指标ITAE的变化曲线

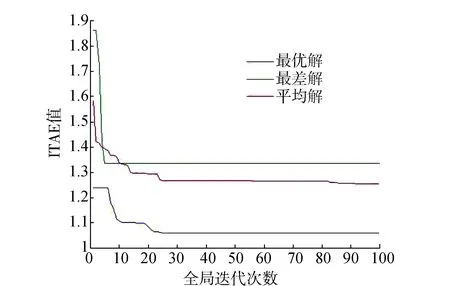
图5 基于PSO求解的PID性能指标ITAE的变化曲线

两种智能算法求解得到最优的PID参数后，该系统的阶跃响应如图6所示，由此可知，对于不稳定的被控对象，两种算法智能求解得到的最优PID控制器的参数Kp，Ki，Kd均可以使用，但是通过混合蛙跳算法整定后得到的系统阶跃响应,其超调量比PSO算法整定的超调量小，从而相对稳定性好, 而且调整时间快，系统的偏差达到最小。

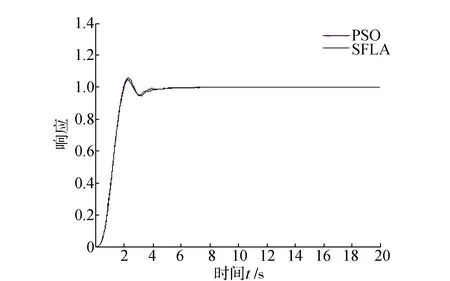
图6 基于PSO和SFLA求解得到的最优参数对应的单位阶跃响应曲线

4 结论

1)PID控制器的参数整定对于不稳定的实际被控系统至关重要，其数学模型是一个存在多个局部最优的复杂模型，通过引入新型的智能优化算法，从而快速、准确地找到最优参数值，是一种迫切需要的求解方法。

2)提出了基于SFLA算法的PID参数整定方法，在被控对象数学模型已知条件下，通过仿真对比试验，无论是收敛精度和收敛速度，SFLA均优于PSO算法，从而证明该方法在离线时整定与优化的可行性和有效性。但将本方法用到在线整定与优化时会涉及到SFLA算法的效率问题，该问题与其参数设置有关，如何提高整定与优化效率将另文讨论。

[1] 韩帮华. PID控制器参数整定方法及应用研究[D]. 青岛：青岛科技大学, 2009.

[3] 王建平, 赵婵娟. 基于PLC的专家PID控制算法在精密压药液压机控制系统中的应用[J]. 化工自动化及仪表, 2016, 43(6):579-583.

[4] 张玲娜, 马艳, 张建军. PID控制与模糊PID控制在电机调速系统中的比较与仿真[J]. 自动化与仪器仪表, 2016(7):52-54.

[5] 韩玉敏, 王希凤. 基于模糊控制的锅炉汽包水位控制系统的研究[J]. 黑龙江工程学院学报, 2016, 30(6):20-23.

[6] 徐传敬, 赵敏, 李天明. 一种改进遗传算法的PID参数整定研究[J]. 计算机技术与发展, 2016, 26(9):12-15.

[7] 赵亚琪, 王景成, 张浪文,等. 基于粒子群算法的TBM液压系统PID参数优化[J]. 控制工程, 2016, 23 (8): 1242-1246.

[8] 邢峰. 蚁群参数寻优自适应PID控制实验研究[J]. 机械设计与制造, 2016(7):157-159.

[9] EUSUFF M, LANSEY K, PASHA F. Shuffled frog-leaping algorithm: a memetic meta-heuristic for discrete optimization[J]. Engineering Optimization, 2006, 38(2):129-154.

[10] 赵转哲. 混合蛙跳算法的改进及在旋转机械故障诊断中的应用研究[D]. 南京:东南大学, 2016.

[11] ZHAO Z, XU Q, JIA M. Sensor network optimization of gearbox based on dependence matrix and improved discrete shuffled frog leaping algorithm[J]. Natural Computing, 2016, 15(4):653-664.

[12] ZHAO Z, XU Q, JIA M. Improved shuffled frog leaping algorithm-based BP neural network and its application in bearing early fault diagnosis[J]. Neural Computing and Applications, 2016, 27(2):375-385.

[13] 柴天佑, 张贵军. 基于给定的相位裕度和幅值裕度的PID 参数自整定新方法[J]. 自动化学报, 1997, 23 (2) : 167 - 172.

[14] AWOUDA A E A, BIN M R. New PID tuning rule using ITAE criteria[J]. International Journal of Engineering, 2010, 3(6):171-176.

[15] 郁磊, 史峰, 王辉. MATLAB智能算法30个案例分析[M]. 北京：北京航空航天大学出版社, 2015：137-143.

PID control parameters tuning based on shuffled frog leaping algorithm

ZHAO Zhuanzhe1, HE Kang2, HE Huijuan1

(1.School of Mechanical and Automotive Engineering, Anhui Polytechnic University, Wuhu 241000, China;2.School of Mechanical and Electronic Engineering, Suzhou University, Suzhou 234000, China)

PID controllers are widely used in process industry, but the traditional PID parameter tuning method has been unable to fully meet the development of modern industry. The shuffled frog leaping algorithm (SFLA) is a swarm intelligent algorithm based on memetic meta-heuristic search which has been used on the three parameters tuning or optimization of PID control system in this paper. Combined with the Simulink model, the MATLAB simulation off-line experiment is carried out. The experimental result shows that SFLA is more accurate and stable than the particle swarm optimization (PSO) algorithm. As an intelligent solution method, the SFLA has good practical value.

shuffled frog leaping algorithm; PID control; MATLAB simulink; parameter tuning

10.19352/j.cnki.issn1671-4679.2017.06.008

2017-05-31

安徽省高校自然科学研究重点项目(KJ2016A803, KJ2017A439)；安徽省省级大学生创新创业训练计划项目(201510363163)

赵转哲(1979-)，男，讲师，博士，研究方向：智能控制；机械故障诊断.

TG156

A

1671-4679(2017)06-0038-04

[责任编辑：郝丽英]