基于优先原则的启发式算法在ZM项目中的应用

孟瑶琳，张建国

（1.西安长庆科技工程有限责任公司，陕西西安 710018；2.上海城投原水有限公司教育培训中心，上海 200120）

基于优先原则的启发式算法在ZM项目中的应用

孟瑶琳1，张建国2

（1.西安长庆科技工程有限责任公司，陕西西安 710018；2.上海城投原水有限公司教育培训中心，上海 200120）

施工进度计划的科学编制及合理安排是项目进度管理的重要内容，是影响项目工期目标实现的关键环节。通过关键路径法得到ZM项目建设最短工期进度计划，再从资源约束的角度，采用启发式算法对项目进度计划重新进行调整和编制，得出资源配置最优的工期。

项目进度；优先原则；启发式算法；优化模型

1 项目数据提炼

ZM项目是某油气管道工程的一座油气合建一级站场。具备计量、分输、清管及增压等功能。项目合同工期18个月（560d）。按照项目的施工顺序步骤，对项目进行工作结构分解。并对该项目涉及的各活动步骤，进行逻辑关系列表。具体如表1所示：

表1 ZM项目活动逻辑关系表

按上表所列逻辑关系顺序，可以绘制ZM项目的单代号项目网络图。

对各活动的最短工期和最长工期进行估算，在估算活动的持续时间时，主要使用定额计算和专家调查等两种方法，其中定额计算主要针对项目中总图工程、单体建筑工程和绿化工程等三部分，而对于工艺管道工程、储罐工程和安装工程因可能涉及到新工艺、新方法或新材料，所以借助具有丰富施工经验的专家给出活动持续的估算时间。具体如表2所示：

2 项目进度优化模型构建及求解

2.1 预估优化工期

Matlab是矩阵实验室（Matrix Laboratory）的简称，本文采用了Matlab的遗传算法工具箱。为了保证分项任务工期确定的准确性，在任务结构重新分解时将各项任务的工期调整为区间的形式，在真正优化开始之前，可以先采用标准遗传算法对工期区间内的潜在最优工期求解，再通过基于优先原则的启发式算法进行调整。

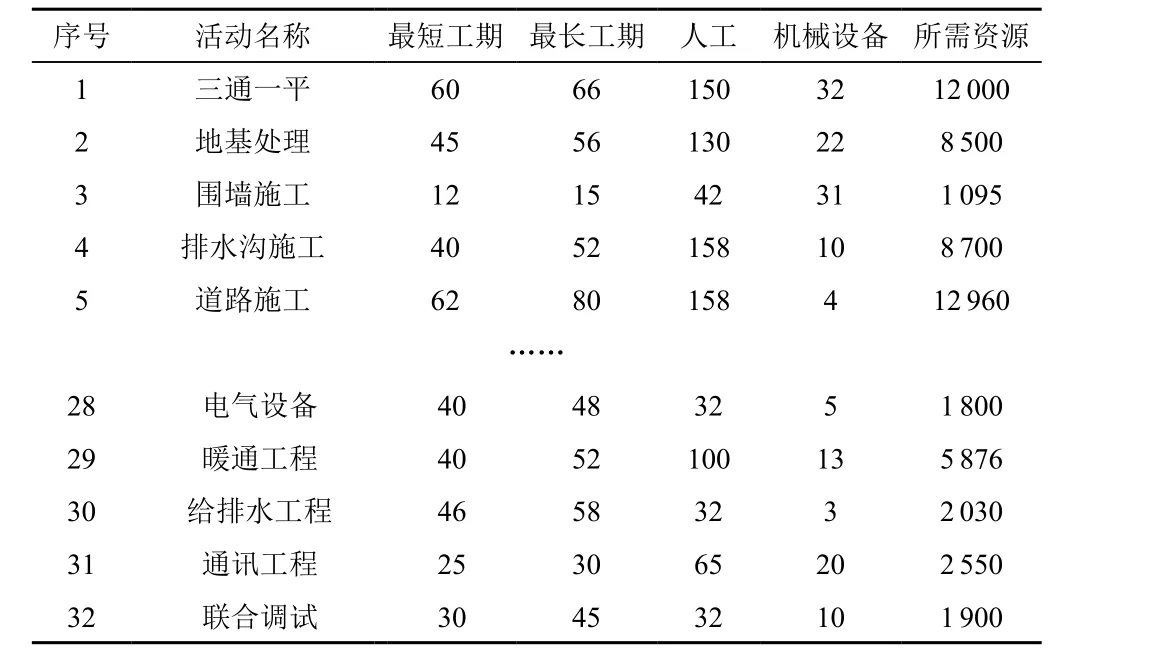
表2 ZM项目工期及资源需求表

本次研究中所用的标准遗传算法采用双精度浮点数编码的方式，交叉概率为0.6，函数自变量数值为32，初始种群生成方式为随机，变异方式为均匀变异，概率为0.03，具体的运算流程可以参考任少锋[6]的实现方法采用Matlab软件全局优化工具箱中的遗传算法图形操作界面进行参数设置，并执行算法。具体的潜在最短工期优化运算结果如下表3所示：

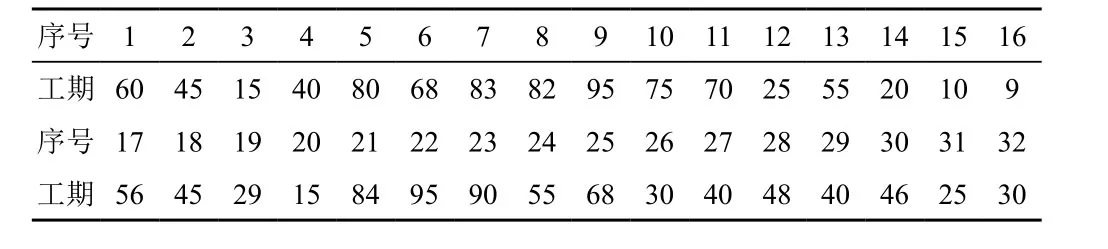
表3 项目潜在最短工期优化结果表

2.2 优先原则的确定

启发式算法是指在一个随机的群体寻优过程中，个体能够利用自身或者全局的经验来制定各自的搜索策略，是一种有目的或者有策略的方法。基于优先原则的启发式算法主要由调度生成机制和优先规则两部分构成，本文选用串行调度机制来生成调度计划。本文分别选取最小总时差、最短任务工期和最大资源日均需求量等三个优先原则，并比较应用三种优先规则产生的结果，选取输出结果中总工期最小的作为资源配置最优的项目进度计划优化方案。具体的假设包括：

（1）项目各任务的工期在一个区间范围内可变，且只能取整数；

（2）项目执行过程中只存在人工和机械资源约束；（3）资源的日均可用量是一个已知常量。

2.3 优化模型

因为建立此模型的目的是使项目在实施的过程中工期最小化，所以此模型以整个项目的总工期（T）最短为目标。

目标函数：

约束条件：

（1）任务工期约束，即各任务的工期必须在确定的范围内变化：

式中：

N 为ZMYQ合建站项目所包含的活动数，N=32；

t（q）为任务 q 的计划工期；

LB（q）为任务 q 的可能最短工期；

UB（q）为任务 q 的可能最长工期。

（2）各任务的逻辑关系不能违背，即各任务必须在其所有的紧前任务完成之后才能开始：

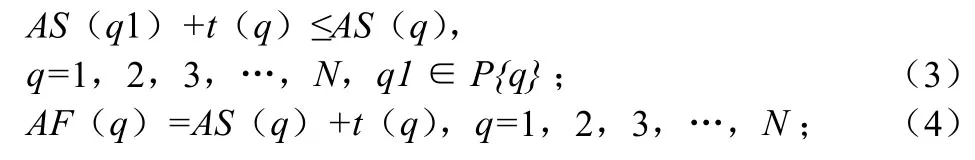
式中：

AS（q）为任务 q 的计划开始时间；

AF（q）为任务 q 的计划结束时间。

（3）每个工作日内，所有任务对资源的总需求量不能大于资源的可用量：

式中：

Ts 为可能工期的最大值，Ts=1 842；

i 为时间参数，其中 i=1，2，3，…，Ts；

ResA（i）为第 i 个工作日资源的总可用量，初始值为1050（工时）；

ResR（i）为第 i 个工作日资源的总需求量；

Set（i）为第 i 个工作日，所有进行中的任务的集合；Res（q）为完成任务 q 所需要的资源总量；res（q）为任务 q 工期内的资源日均需求量。

2.4 具体运算流程

第1步：定义函数和初始化运算流程，其中基础函数包括各任务的工期t（q），任务所需投入的资源总量Res（q），任务的日均资源需求量ResR（i），P{N}为各任务的直接紧前任务集，B{N}为各任务的直接紧后任务集，ResA（i）代表项目工期内的日均资源可用量等，任务在可安排任务集中的状态（0为不可安排，1为可安排）。

第2步：考察D（N）中为1的元素，将其列标放入数组Lb中，根据优先规则确定本次予以调度的项目任务，当优先原则为最小总时差时，考察TF中以数组Lb中数值为列标的元素，确定其最小值，将其列标赋给变量N；当优先原则为最小任务工期时，考察t中以数组Lb中数值为列标的元素，确定其最大值，将其列标赋给变量N；当优先原则为最大资源日需求量时，考察res中以数组Lb中数值为列标的元素，确定其最大值，将其列标赋给变量N。如确定数组Lb中最大/小值有多个元素相等，则取其中列标值小的赋给变量N，即本次要进行安排的是任务N。

第3步：将满足逻辑关系约束和资源约束的任务最早开始时间确定为计划开始时间AS（N），再根据项目各任务工期计算得到各任务的计划结束时间AF（N）=AS（N）+t（N）。

第4步：已安排的任务N移出可安排任务集，并依据任务逻辑关系分析其紧前或紧后任务是否均已经安排完毕，如确定则将其安排至可安排任务集中，供下一步备选。

第5步：重复进行步骤第2、3、4的操作，直到所有的任务均完成调度，算法结束。

第6步：根据已得到的各任务计划结束时间，确定项目总工期 T1=MaxAF（q）。

第7步：按照以上步骤，分别用三种优先规则确定项目总工期T1，T2，T3，得到最优结果即 T→Min（T1，T2，T3）。

具体的编程通过运用 Matlab 软件计算机编程语言加以实现，得到针对项目各任务工期范围内的一组确定的任务工期值，来进行项目调度，生成项目进度计划方案，进而得到资源配置优化条件下的项目最小总工期，具体优化程序见论文后面的附录中。

3 模型运算结果

将上文中得到的预估最优任务工期结果作为已知的数据，输入编制的启发式算法程序中，具体的计算结果如下表4所示：

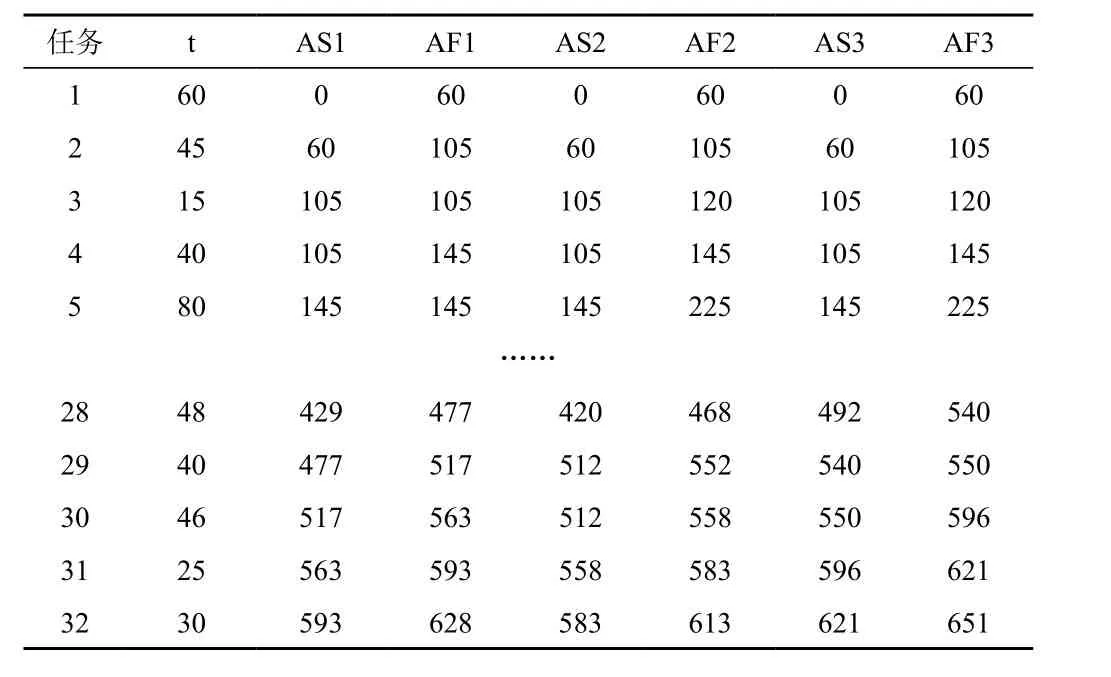
表4 模型运算结果

通过上表的计算结果可以明确，T=Min（AF2）=613d，即在资源限制条件下，以最短任务工期为优先条件的总项目工期为最短总工期613d。

4 总结

可以看出，在无资源约束的条件下，即假定该项目所有资源均满足使用要求的前提下，该项目的合同签订工期为18个月（560d）。而根据项目运行的实际情况，在考虑了资源的限制条件后，利用启发式算法，可以得出该项目的最优解工期为T2=613d，虽然相比合同工期延期53d，但是避免了人工和机械设备的占用冲突，提前缓解了项目实施中可能遭遇的资源问题，降低了项目运行风险，使有效资源利用率得到最大保障。

[1] 李建平.现代项目进度管理[M].北京：机械工业出版社，2008.

[2] Kerzner H.Project Management：A Systems Approach to Planning，Scheduling and Controlling[M].John Wiley & Sons Inc.，2009.

[3] 刘伊生.工程项目进度计划与控制[M].北京：中国建筑工业出版社，2008.

[4] 卢向南.项目计划与控制[M].北京：机械工业出版社，2009.

[5] 何正文，刘人境，徐渝.基于随机活动工期的资源约束项目鲁棒性调度优化[J].系统工程理论与实践，2013，（3）：650-659.

[6] 任少峰.基于模糊关键链的港铁列车项目进度计划优化设计[D].长春：吉林大学，2014.

Application of Heuristic Algorithm Based on Priority Principle in ZM Project

Meng Yao-lin，Zhang Jian-guo

The scientific preparation and reasonable arrangement of construction schedule is an important content of project schedule management，and is the key link affecting the realization of the project schedule target.The critical path method to get the shortest time ZM project construction schedule，from the resource constraint perspective，using heuristic algorithm to re adjust and prepare the project schedule，the optimal allocation of resources in the construction period.

project schedule；priority principle；heuristic algorithm；optimization model

O342

B

1003-6490（2017）12-0242-02

2017-10-09

孟瑶琳（1985—），女，陕西西安人，工程师，主要从事场地总图设计研究工作。