基于动态阈值的变压器异常状态检测*

刘勇，尹豪杰，张星海，范松海，严磊，高波

（1.国网四川省电力公司，成都610041；2.西南交通大学 电气工程学院，成都610031）

0 引 言

电力变压器作为电力系统能量转换和传输的关键设备，因受电、热、机械等多种应力，以及水分、氧气等多种因素共同作用，其主绝缘性能会逐渐下降并最终失效［1-2］。在长时间不间断和高负荷运行状态下，各种电、热故障会随着设备服役年限的增长而逐步增多。在变压器绝缘状态在线监测系统中，油中溶解气体分析（Dissolved Gas Analysis，DGA）是目前在工程应用中能够对变压器整体绝缘状态进行实时监测和跟踪的最为可靠、有效的方式［3-4］。

传统Duval三角法、Doernenburg法、Rogers比值法、IEEE气体含量以及 IEC三比值法［5-9］，主要以H2、CH4、C2H2、C2H4和 C2H6这5种气体相对含量及比值等数据为基础，对变压器内部可能出现的故障状态进行判断，得到了广泛认可与应用。然而，通过一系列现场运行情况与研究结果发现，此类方法仍然存在两方面的局限性：（1）编码不全，对部分比值编码缺乏相关说明，无对应故障类型；（2）对早期故障难以发现，通过比值得到的结果只是设备故障状态的判定和说明，对于设备早期故障难以预警。对于不同容量、不同电压等级、不同运行年限、不同地区和不同载荷的变压器而言，故障特征也不尽相同。

DGA作为反映变压器主绝缘性能优劣的关键方法，在一定程度上受上述因素影响。同时，受在线监测设备性能的限制，DGA结果也因监测设备不同而略有差别。如果DGA数据不准确或出现偏差，会影响到变压器绝缘状态最终诊断结果，引起虚警、漏报，甚至造成不必要的检修损失。为此，基于现有设备及其所测数据，充分考虑上述各种影响，采用各种数据分析、处理手段，对于变压器状态的准确评估和预警十分必要。

动态阈值（Dynamical Threshold，DT）法作为交通运输领域进行交通流量监测的主要方式，认为在一定的时间范围内，监测数据的取值必然在一个合理的数值取件范围内，如超出这一区间，可认为这一监测数据异常［10］。变压器状态监/检测数据除DGA数据外，还包括负荷、油温及绕组温度等一系列关键数据。受到电压等级、变压器容量及负荷波动等因素的影响，DGA数据会产生不同程度的变化。同时，不同变压器运行状态也会因以上因素的影响而各异，采用统一阈值判断设备运行状态难免会出现对真实情况判断不准的问题。

为此，文章在以标准给定值判断变压器状态的基础上，引入动态阈值理论，以设备运行当前、历史及检修数据为基础，对变压器在线监测数据、历史数据、台账和检修记录等信息进行阈值划分，采用贝叶斯网络（Bayesian Network，BN）求解变压器各种可能运行状态的概率，对变压器潜在异常状态进行检测。

1 基础动态阈值模型

1.1 变压器在线监测数据特征

近年来，电力设备在线监测系统日臻完善，电力监测大数据逐渐形成。从数据形成机理方面考虑，电力设备监测大数据的特征包括以下几个方面：

（1）时间序列相关性：电力设备在线监测数据属于时间序列数据，随时间连续变化，存在一定的动态发展趋势；

（2）空间数据相关性：电力设备在线监测数据与最近一段时间或周期监测到的数据的平均值存在一定的相关性；

（3）历史数据相关性：电力设备状态检测数据的具有一定的周期性和发展趋势，在线检测数据与历史数据存在一定的相关性；

（4）多种异常状态共存：对于同一设备，通过不同的监测数据分析，可能得到多种异常运行状态；

（5）多种在线监测数据之间存在相关性：电力设备各种状态检测数据之间存在一定的相关性，如变压器油温与负荷数据。

1.2 变压器基础阈值模型

根据阈值理论［10］，对于反映设备运行状态的不同特征量Xi（i=1，2，…）等，其取值范围为：

式中xmin和xmax为xi在某一状态的阈值，取值为固定值。

对于变压器在线监测数据，油色谱数据、油温数据和负荷数据是反映其运行状态的几个主要指标。以油色谱数据为例，设q、v、c分别为油中溶解气体的相对含量、相对增长速率和总烃含量，则根据传统阈值判断方法有：

式中 qmin和 qmax为标准规定 H2、CH4、C2H2、C2H4和C2H6这5种气体的相对含量对应不同状态的阈值；vmin和vmax为5种气体的增长速率阈值；cmin和cmax为总烃含量阈值。

传统的状态评估方法以相关标准给出的固定阈值为判断标准，没有较多的考虑监测数据的的时间序列相关性、历史数据相关性和数据之间的相关性［8］。基于阈值理论，认为在一定的时间间隔内，各种时间序列的监测数据必然在一个合理的数值区间内，这一区间称为阈值区间，若超出了既定区间，则认为该条数据异常。

为此，变压器油中溶解气体含量阈值以其各种可能运行状态为基础（g），考虑变压器t时刻的运行状态（Ct）受时间序列数据（VT），空间数据（VS）和历史数据（VH）的综合影响（h），并且各在线检测数据之间的关系存在一定的相关性（f）。

因此，变压器运行状态的动态阈值模型可以用如下三阶段模刻画：

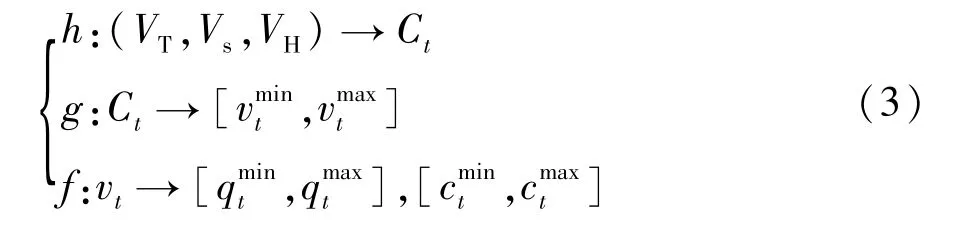
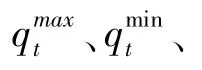
1.3 基于动态阈值模型的异常数据识别

根据 IEC 60599及 DL/T 722-2000规定［11］，当变压器油中溶解气体总烃含量或H2大于150 ppm，或C2H2含量大于5 ppm（对于500 kV以上电压等级变压器为1 ppm）以及CO含量大于300 ppm（或相对产气速率大于10%）时，应引起注意，具体如表1和表2所示。

表1 氢、烃气体含量限值判断（封闭式）Tab.1 Estimation threshold value of hydrogen and hydrocarbon gases（closed type）

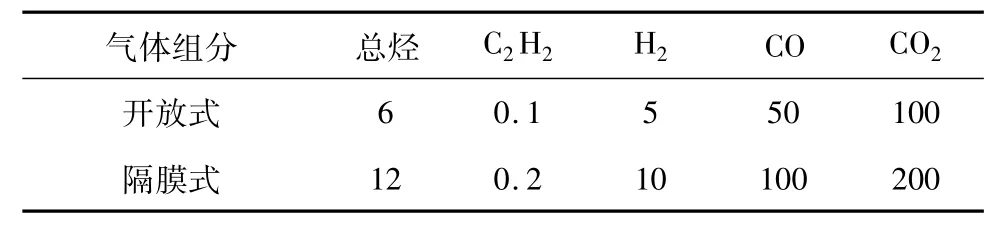
表2 气体增长速率注意值（mL/d）［7］Tab.2 Note values of gas growth rate［7］

（1）基于IEC、IEEE和DL/T相关导则，应用时间序列数据、空间数据和历史数据实现t时刻变压器的状态推算；

（2）基于速度、各组分气体含量以及总烃含量阈值，对气体增长速率、气体含量和总烃含量进行判断，如果在阈值以内，则标记为正确数据，进行下一步，否则停止，标记为异常数据。

对于变压器运行状态，仍以表1给出的3种状态为基础，应用大量油色谱在线数据推算变压器状态较为复杂。为此，基于表1将VT、VS、VH转化为相应变压器状态CT、CS和CH，然后计算Ct，即式3中给出的 h：（VT，VS，VH）→Ct。为后续计算方便，将三种状态分别记为1、2和3，即：正常为1，注意为2，故障为3。

考虑到与变压器运行状态相相关的DGA和油温数据，包括时间序列数据、空间数据和历史数据样本量较大，将其作进一步简化。取前一时刻的数据Vt-1代表时间序列数据，取前多个连续时刻的数据平均值VSt代表空间数据，取不同天同时刻历史数据VHt代表历史数据。此时，式（3）可转化为：

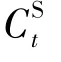
1.4 基于贝叶斯网络的变压器运行状态推算

贝叶斯网络（Bayesian Networks，BN）作为一种新的知识表示模型和推理方法［12］，它使用概率论来处理知识的不确定性，本文将其应用于变压器状态推算，具体如图1所示。

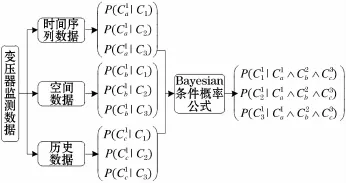
图1 基于BN的变压器状态推算过程Fig.1 Calculation process of transformer condition based on Bayesian network

根据 VT、VS和 VH推算的变压器运行状态的概率［10］：

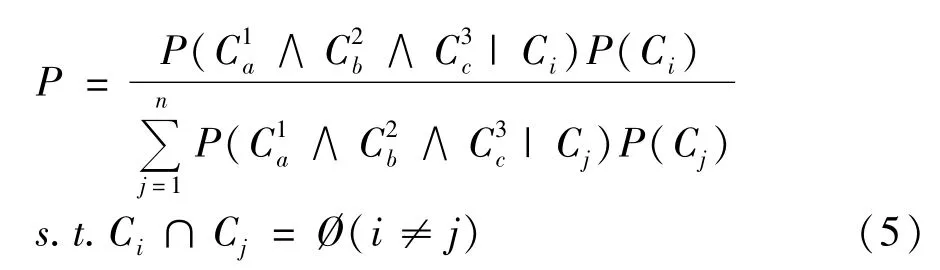
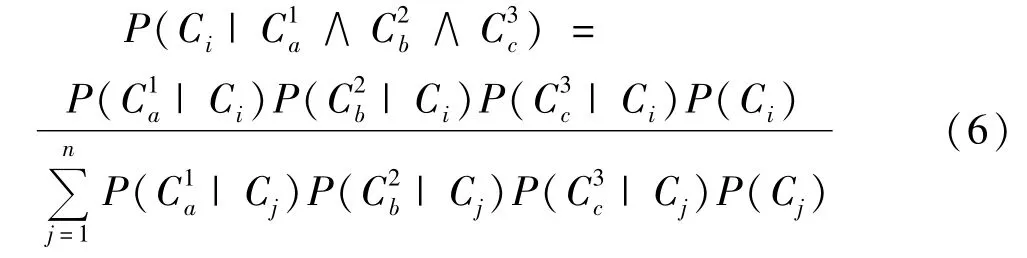
为求解式（6），依Bayesian理论，需要用到的先验知识包括 P（C1a|Ci），P（C1b|Ci），P（C1c|Ci）和P（Ci），可通过相应历史或在线数据获得。

依据时间序列数据、空间数据、历史数据可以推算t时刻各个可能状态的取值：

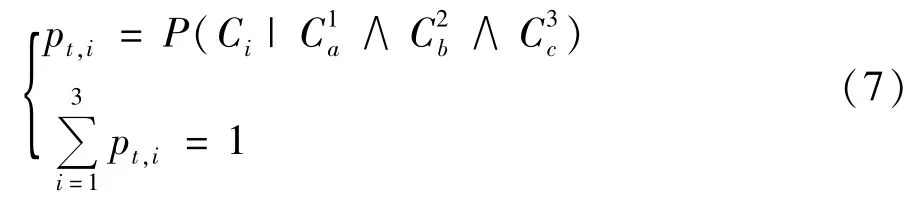
式中 pt，i为变压器在t时刻状态为i的可能性。

同样，对于变压器每一种可能状态下的油中气体增长速率，有如下模型：

2 案例分析

表3给出了某500 kV电力变压器A相（总油重71 t）在2014年间检修前后三个月内的油色谱数据，每三天记录一次数据，因故障在10月11日停运检修，经停电检修并滤油后于10月14日继续恢复运行，后又发现设备异常过热。根据检修记录，该A相主变在前期并无其他异常情况。由表3可以看出，各种可燃气体（H2、CH4、C2H6、C2H4和 C2H2）及 CO含量均小于标准规定值，为此，仅对表2规定的各增长速率进行分析。

考虑到气体含量与相对增长速率之间的关系可用式（9）进行描述［13］：

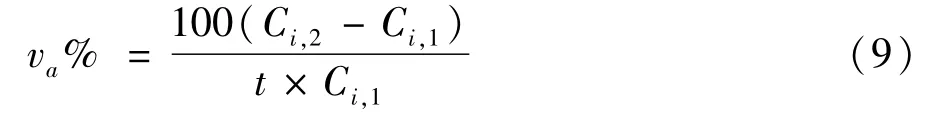
式中 Ci，2和 Ci，1分别为第二次和第一次取样测得油中某气体浓度，μL/L；t为二次取样时间间隔中的实际运行时间。

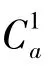
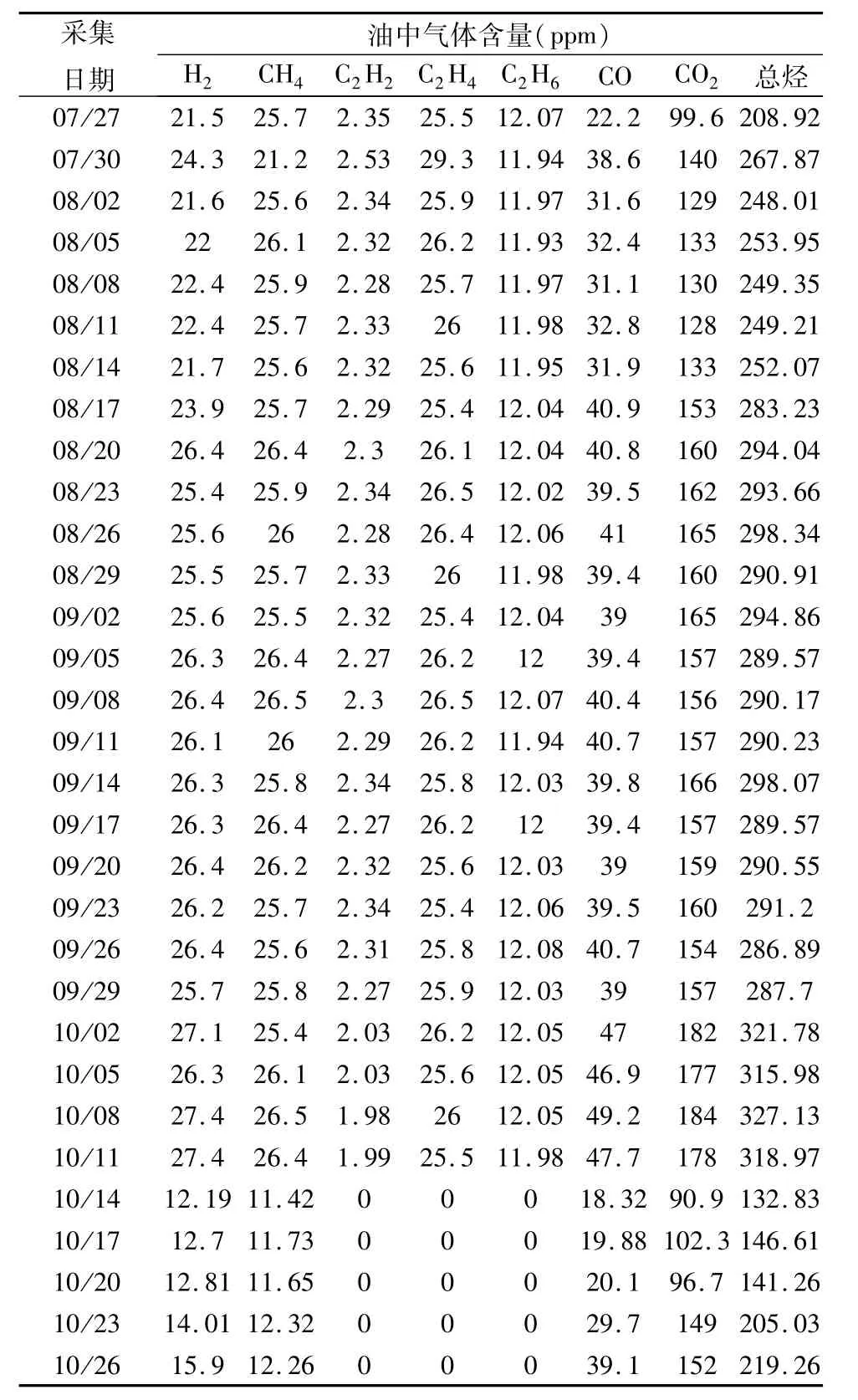
表3 某500 kV电力变压器3个月油色谱数据Tab.3 Dissolved gas data of one 500 kV power transformer within 3 months

则有：

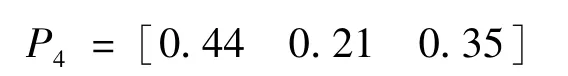
用p1，p2和p3分别表示正常、注意和异常三种状态可能发生的概率，结合式（5）至式（10）及上述先验概率，得到不同阈值准则下的总烃增长速率判断结果如表4所示。

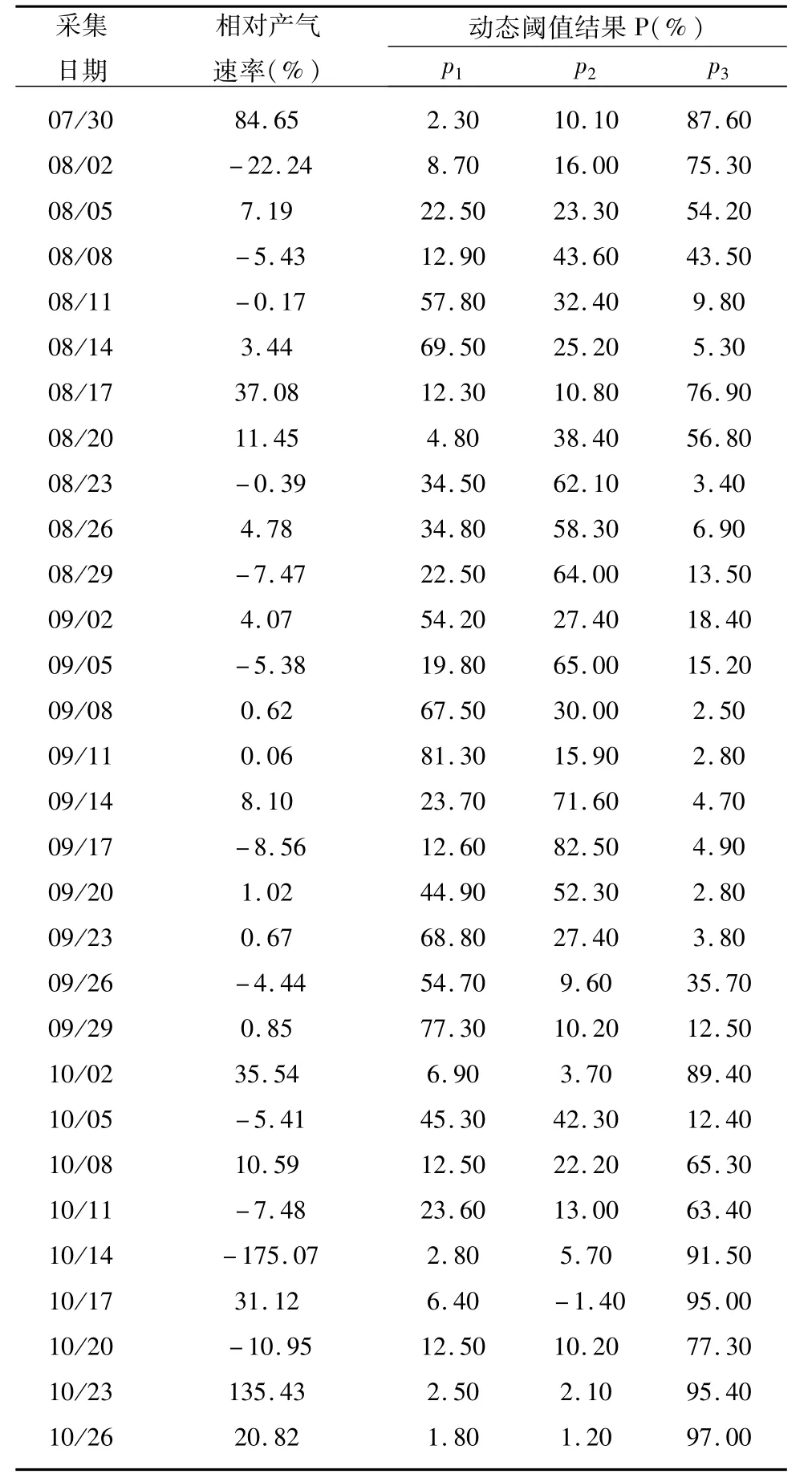
表4 变压器状态推算结果Tab.4 Calculation result of transformer condition

由表4可以看出根据标准给出的总烃含量相对产气速率判断，在变压器停运检修前期，共有6次超标，其结果均超过标准规定的10%，检修后两周内总烃仍保持较高增长速率，所采5次数据均为异常状态。然而，基于动态阈值模型，可以看到在故障前，除基于标准判定的6次异常状态，8月5日和10月11日两日总烃增长速率的异常概率均超过50%。在变压器检修重新投运后，其异常概率仍保持较高水平（最低77.3%），这与实际变压器运行情况相符。可以看出，与传统标准给定的阈值判定方法相比，所提动态阈值对于变压器状态监测具有更高的可靠性。

为进一步验证所提方法的有效性与通用性，基于某省供电公司所辖33个变电站中47台曾存在异常或故障检修记录的主变进行分析，主变信息如表5所示，分析数据采用变压器当时运行DGA数据。鉴于篇幅，油中溶解气体数据在此不再列出。同样，由表5可以看出，对于8台330 kV变压器，基于IEC标准的判断结果和基于动态阈值评估结果相同，状态为正常、注意和异常的数量相同；但对于110 kV、220 kV和500 kV等级的变压器，本文方法评估结果为注意异常的数量较标准方法稍多，通过对比故障检修记录，发现本文方法比传统方法可靠性更高。

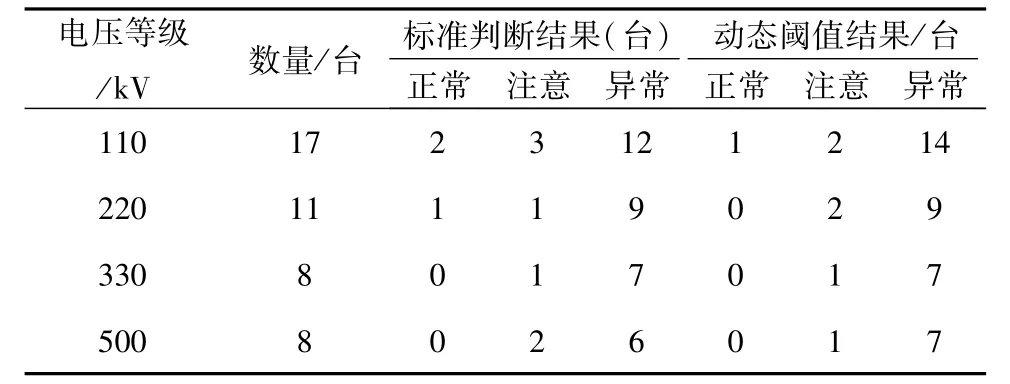
表5 参与评估变压器基本信息Tab.5 Basic information for transformer assessment

3 结束语

在电力变压器状态评估过程中，基于标准阈值的评判方法因有效可靠得到了广泛应用，但其仍存在一定的局限性。本文在传统标准阈值评估的基础上，引入态阈值理论建立变压器运行状态动态阈值评估模型，并采用贝叶斯网络对变压器运行状态进行求解。基于实际运行数据计算分析结果表明：

（1）基于动态阈值的变压器状态评估方法，是基础传统标准阈值基础的改进方法，具有比传统阈值方法更高的准确性；

（2）采用贝叶斯网络求解并结合实测数据求解变压器运行状态，充分利用了贝叶斯网络在状态推算方面的优势，且所得结果较传统方法相比更具可靠性。