基于行波固有频率和VMD的T型输电线路故障定位*
2017-12-18张媛媛朱永利张宁张蒙郑艳艳黄晓胤
张媛媛,朱永利,张宁,张蒙,郑艳艳,黄晓胤
(1.华北电力大学电气与电子工程学院,河北保定071003;2.冀北电力公司检修分公司,北京102488)
0 引 言
目前,行波法在高压输电线路故障定位中具有广泛的应用[1]。基于行波的输电线路测距方法包括单端行波法[2]和双端行波法[3]。其中,单端行波法仅需一端故障行波信息即可进行故障测距,但是对于行波反射波头的准确检测存在一定的难度。双端行波法无需识别反射波头,但对GPS对时装置的精度要求太高,可靠性较低。基于此,一些学者提出了基于行波固有频率的故障定位方法[4-7]。
基于行波固有频率的故障定位方法不受行波反射波头检测的制约,其核心问题是进行固有频率的提取。由于故障行波在故障点以及母线端会发生不同程度的折射与反射,容易引起固有频率的混叠现象,从而造成提取到的固有频率主成分存在误差。基于此,文献[8]提出利用多重交织抽样的方法消除频谱混叠,但该方法在处理电力系统暂态信号时适用性较差。随着科研成果的不断创新,一些学者提出了 EMD[9]和 EEMD[6]方法,该方法可以很好地应用于电力系统中,但是并不能完全消除模态混叠。并且,目前关于行波固有频率故障测距方面的研究大多针对于单回输电线路以及同杆并架线路[10-12],而对于结构较复杂的T型输电线路却鲜有研究。
针对以上问题,提出一种基于行波固有频率和变分模态分解(Variational Mode Decomposition,VMD)的T型输电线路故障定位方法。VMD方法[13]是最新提出的一种信号分解方法,它克服了传统方法无法完全消除模态混叠的弊端,具有良好的模态稳定性。本文首先应用VMD方法对故障行波进行模态分解,然后提取出固有频率主成分,通过相应支路固有频率主成分的大小比较判定出故障区间,最后进行故障定位。仿真结果表明,该方法不受波头检测和同步时钟的限制,具有较高的故障定位精度。
1 VMD方法原理
VMD方法的中心思想是变分问题,分为变分问题的构造以及求解两部分。假设每个模态是具有中心频率的有限带宽,将故障行波信号分解为k个模态分量,使得所有分量的估计带宽之和最小。


式中 {uk}:={u1,…,uK}代表 K个 IMF分量;{ωk}:{ω1,…,ωK}代表每个分量的中心频率。
求取上述模型的最优解,引入Lagrange函数,将约束性变分问题转化为非约束性问题,即:

通过交替更新ukn+1、ωkn+1和 λn+1求得上式的“鞍点”,具体算法步骤如下:
(2)以下两式为基准,更新uk和ωk:
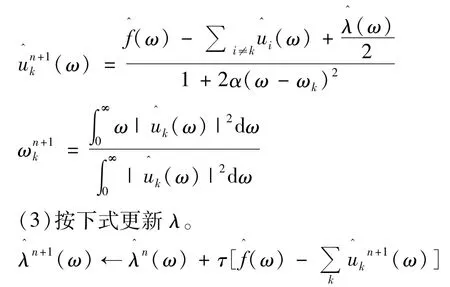
VMD算法实现了各模态分量在频域范围的反复更新,能够将频率相近的谐波分量成功分离。本文将VMD方法分解出的首个IMF分量经过多信号分类(MUSIC)[14]方法提取出固有频率主成分,为得到精确的故障距离奠定了基础。
MUSIC方法是一种基于参数的谱估计方法,能够分辨频率十分相近的复指数信号,即使是在行波衰减速度快、行波信号短的情况下依然具有很高的估计精度。因此,将VMD与MUSIC算法相结合,实现固有频率主成分的准确提取。
2 故障定位原理
2.1 固有频率法
故障行波在有损输电线路上传播时具有无限多种波速,在间断点具有无限多个反射系数,在频域上表现为一系列特定频率的谐波形式,称之为固有频率[15]。文献[9]给出了应用固有频率得到故障距离的计算式:

式中 θM表示故障行波信号在本端母线的反射角;θF表示故障行波信号在故障点的反射角;vk表示频率fk下的行波波速,其中,Zs、Ys为输电线路的序阻抗与序导纳。
由于过渡电阻在故障初始阶段近似为纯阻性,因而θF取为π。θM的计算公式如下:

综合式(3)与式(4)得到故障距离随频率变化的表达式:

式中 R、L分别表示系统等效电阻和电感;f表示提取出的固有频率;Rm、Lm、Gm、Cm分别表示线路单位长度的模电阻、电感、电导和电容。对上式求导数,可知故障距离d随着频率f的增大而减小。据此,可以通过比较固有频率的大小关系来确定故障点距离母线测量端的远近。
2.2 故障区间的判定原理
T型输电线路模型如图1所示,故障行波信号测量装置分别安装于M、N、P三端。假设结点T处发生短路故障,由于故障附加电压的作用,输电线路上将会产生向各端传播的故障行波信号,对该行波信号进行固有频率的提取,得到T节点故障时传播到M、N、P三端的固有频率主成分 fTM、fTN、fTP。根据上小节的证明,可以推断出当故障点发生在某一分支线路上时,对应的母线端测量点提取出的固有频率将大于T节点故障时的固有频率,而非故障分支线路恰恰相反。

图1 T型输电线路示意图Fig.1 Schematic diagram of simulation model for Teed-circuit
因此,可得到不同区间故障时的判据公式为:
(1)故障发生在MT分支

(2)故障发生在NT分支

(3)故障发生在PT分支

(4)故障发生在T结点

式中 fM、fN、fP分别表示M、N、P端提取到的固有频率。由于故障行波经过T节点时会发生折反射,在T节点故障时,各分支的固有频率与相应的节点频率可能不会完全相等。大量仿真证明,固有频率的测量误差在10%之内[6],为了减小误差,将判据公式(9)改为:

因此,当固有频率满足式(10)时,均认为是T结点故障。根据故障位置的不同,将故障区间分成了MT、NT、PT以及T节点故障。根据以上判据公式,即可判定出故障发生的区间。
2.3 故障距离的计算
大量仿真表明,当故障距离增加时固有频率法的测距误差也随之增大,并且故障行波经过T节点时会发生折反射,造成能量损失。因此,为了提高测距结果的准确性,要同时考虑到测距距离小与故障行波不经过T节点两个条件,做出如下规定:
(1)分支线路故障
当分支线路故障时,仅利用本端测量点得到的固有频率计算出距离,记为故障距离。
(2)T节点故障
当为节点故障时,同时利用三端的固有频率信息,分别计算距本端母线的故障距离,然后将各端线路总长度减去非故障支路得到的距离,即得到应用非故障支路的频率计算出的故障距离,然后求平均,得到T节点附近故障时的故障距离。
2.4 故障定位流程
所提故障定位方法的流程图如图2所示。由图2可知,将结构较为复杂的T型线路首先进行故障分支的判断,然后进行故障测距,计算过程简单明了。

图2 故障定位流程图Fig.2 Flow chart of fault location
3 仿真分析
3.1 仿真模型
采用PSCAD/EMTDC对图1所示T型输电线路模型进行故障的电磁暂态过程仿真。系统参数如下:M端电源电压220∠90°kV;N端电源电压209∠80°kV;P端电源电压209∠60°kV;三端电源均为理想电压源。线路L1、L2、L3长度分别为100 km、80 km、60 km。线路的正序和零序参数为:r1=0.0347 Ω/km、x1=0.423Ω/km、b1=2.726μS/km、r0=0.300Ω/km、x0=1.143Ω/km、b0=1.936μS/km。
3.2 实例分析
假设输电线路在距N端检测点60 km处发生三相金属性接地短路,0.2 s时发生故障,持续时间为0.1 s,利用VMD算法对β模故障行波信号进行分解,结果如图3所示。
图3所示的VMD模态分解结果与图4所示的EMD模态分解结果相比,几乎不存在模态混叠,其分解效果更佳。故障行波信号经VMD模态分解之后,其特征信息主要集中在首个IMF分量中,因此,只需对首个IMF分量进行MUSIC频谱分析,便可得到行波固有频率主成分。
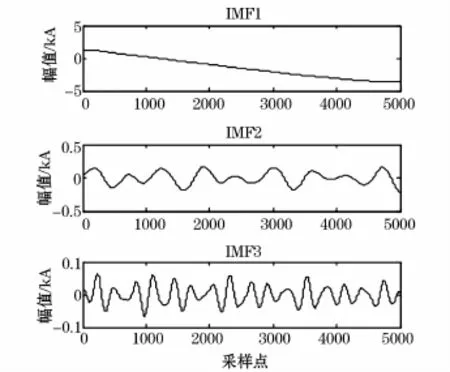
图3 故障行波的VMD分解Fig.3 VMD decomposition of fault traveling wave

图4 故障行波的EMD分解Fig.4 EMD decomposition of fault traveling wave
以M端测点为例,将经VMD分解后的首个分量进行MUSIC频谱分析,得到如图5所示的频谱图,很明显,M端测点检测到的固有频率主成分为fM=1 247 Hz。以同样的方法,得到N端以及P端的固有频率主成分 fN=2 473 Hz,fP=1 850 Hz。
改变故障距离,调整为T节点故障,其他条件不变。对节点故障行波信号进行固有频率主成分的提取,分别为 fMT=1 500 Hz、fNT=1 853 Hz、fPT=2 476 Hz。利用得到的固有频率判断故障支路,相应频率之间进行比较,结果满足式(7),即故障支路为NT。
根据故障行波固有频率,计算NT支路的行波波速为2.978 4×105km/s。系统端为理想的电压源,即端点阻抗为0,因此,其反射系数为-1。可以得到故障距离为:

图5 M端故障行波频谱图Fig.5 Spectrum of traveling wave of M bus

测距误差为218 m。
以上算例表明:通过比较故障点行波固有频率与T节点行波固有频率的大小关系,可以准确的判定出故障支路,并能够依此得到故障距离。
3.3 适应性分析
为了验证所提故障定位算法在T型输电线路中的适应性,表1给出了ABC三相短路故障时不同位置情况下的定位结果。其中故障距离以及测量得到的故障距离均为故障点到相应支路母线的距离。根据表1的测距结果可知,当故障发生在不同位置时,通过本文所提方法可以准确的判断出故障区间,并且,无论是分支故障还是T结点故障,都具有较高的故障定位精度。

表1 不同故障距离时的定位结果Tab.1 Fault location results of different fault positions
假设故障发生在距离M端50 km处,表2、表3、表4分别给出了不同故障类型(故障电阻为0,故障初相角为90°)、不同故障电阻(故障类型为ABC三相短路,故障初相角为90°)以及不同故障初相角(故障电阻为0,故障类型为ABC三相短路)时的测距结果。
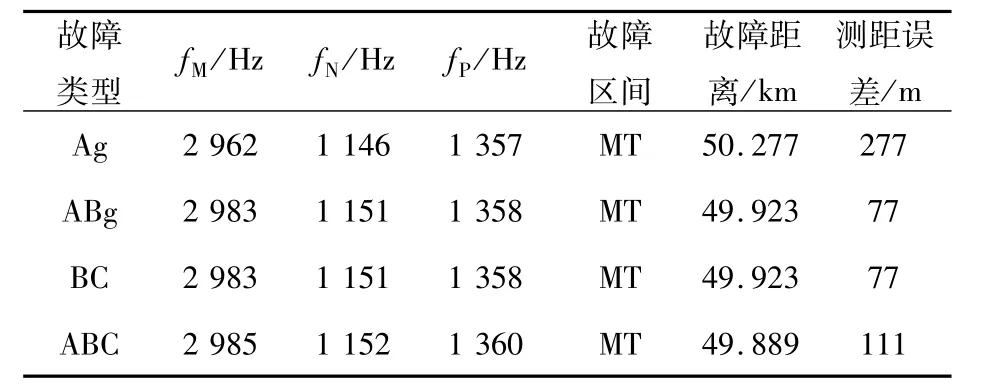
表2 不同故障类型时的定位结果Tab.2 Fault location results of different fault types
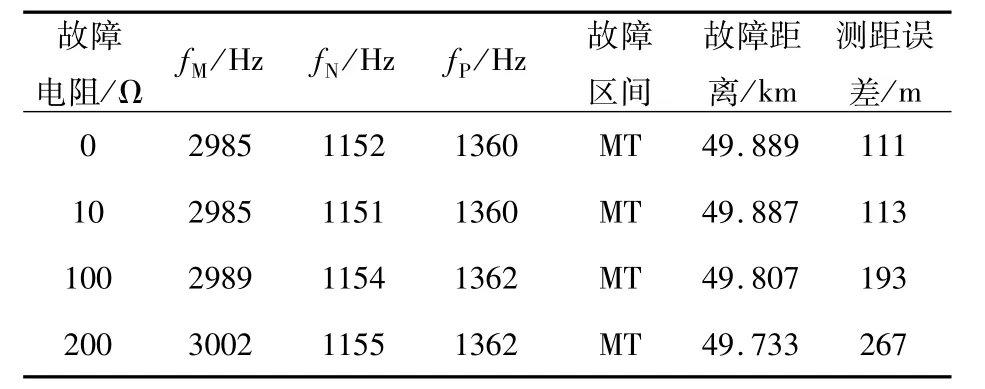
表3 不同故障电阻时的定位结果Tab.3 Fault location results of different fault resistances

表4 不同故障初相角时的定位结果Tab.4 Fault location results of different fault incipient angles
综合以上各表的仿真结果可知,所提故障定位方法克服了故障距离、故障类型、故障电阻以及故障初相角的不同对定位结果的影响,具有较强的适应性和较高的测距精度。
4 结束语
(1)应用VMD算法对故障行波信号进行模态分解,消除了模态混叠现象,提高了对固有频率主成分提取的准确性;
(2)将对应支路上检测到的故障点与T节点故障时固有频率主成分的大小关系进行比较,确定故障区间。该方法原理简单,无需繁琐的计算过程,为实现准确快速的故障定位奠定了基础;
(3)分支故障时,仅利用本端测量点得到的固有频率计算得到故障距离;T结点附近故障时,利用三端测量点的固有频率计算得到故障距离。仿真结果表明,该方法适应性强,定位精度高。
