基于光伏功率等效面积法的多峰最大功率追踪控制方法*
2017-12-18黄思源王鲁杨张浩
黄思源,王鲁杨,张浩
(1.上海电力学院 电气工程学院,上海200090;2.国网安徽淮北市供电公司,安徽 淮北235000)
0 引 言
在光伏系统实际应用中,由于天上移动的云朵、电池板累积的灰尘以及城镇中周围建筑物等的影响,光伏阵列在运行过程中总会受到不同程度的阴影遮挡,太阳能电池板的P-U曲线会受到影响出现多个峰值点。传统的MPPT控制方法在电池板没受到局部阴影影响的情况下可以有效的追踪到电池板的最大功率点,但是对受到遮挡的电池板有时候会跟踪错误,误以为局部最大功率点(LMPP)是全局最大功率点(GMPP)而放弃继续追踪[1]。相应地采用多峰MPPT控制方法可以准确的追踪到光伏组件的全局最大功率点。近年来国内外学者针对多峰追踪控制问题提出很多跟踪方法,如根据复合传统方法的跟踪方法(PI控制算法[2]等)、规律实现跟踪的方法(电流扫描法[3]、电压扫描法等)以及引入人工智能控制算法(神经元网络控制法[4]、模糊逻辑控制法[5]、遗传算法[6]、人工鱼群算法[7]等)的全局寻优跟踪算法等。这些算法都能够较为准确的收敛到全局最大功率点。但这些算法往往存在控制参数多,计算量大,控制思想复杂,追踪速度和精确度成反比,对硬件的要求高等问题,这在一定程度上制约了这些算法的工程实践应用。针对此本文提出了光伏功率等效面积法。光伏功率等效面积法控制思想简单,控制参数少,追踪精度高、速度快,误差小,具有实用价值。
1 非均一照射情况下太阳能电池(P-U)输出特性
1.1 光伏电池数学模型
图1为太阳能电池物理模型等效电路[8],

图1 太阳能电池物理模型等效电路Fig.1 Physical model equivalent circuit of solar cell
由物理模型等效电路图可得出上图各变量的方程式[9]见式(1),式中,I0为太阳能电池内部二极管PN结反向饱和电流,一般情况下为常数;UD为二极管两端端电压,q为电子电荷其值为1.6×10-19C;k为玻尔兹曼常量,0.86×10-4eV/K;T为热力学温度;A为PN结曲线常数(取值范围为1~5)。

通常在实际生活中,生产厂商只提供太阳电池组在标准测试条件下(取标准光照强度Sref=1 000 W/m2、标准温度Tref=25℃)测出的短路电流ISC、开路电压UOC、最大电流Im、最大电压Um。所以当不处于标准测试条件的情况下,必须考虑它们的影响,并对其数学物理模型进行修正[10]。环境温度Tair与电池温度T的关系为:

根据参考光照强度和参考温度可以推算出在新的光照强度和电池温度下的 ISC’、UOC’、Im’、Um’[11-15]:

由文献[11]可知,光伏相关系数 a、b、c的典型值分别为0.002 5℃、0.5、0.002 88℃。根据式(3)所示数学模型,利用MATLAB软件搭建多个太阳能电池模型,然后将太阳能电池进行串联连接,通过给太阳能电池设置不同的温度和光照强度来模拟受到局部阴影影响的光伏阵列仿真模型。
1.2 光伏电池仿真模型
利用根据实际环境因素修正的数学物理模型公式可以搭建出单体太阳能电池,将三个单体电池串联,观察其三块电池处于不同环境下的输出特性。取在标准情况下(Sref=1 000 W/m2、Tref=25℃):ISC=9.2、UOC=34.2、Im=7.95、Um=20、a=0.002 5℃、b=0.002 5℃、c=0.002 88℃。图2为非均一照射条件下的太阳能电池模型仿真图。

图2 非均一照射条件下光伏电池模型仿真Fig.2 Simulation of photovoltaic cell model under non-uniform illumination
为模拟非均一照射的复杂光照环境,每块太阳能电池板都设置了不同的光照强度和温度,三块电池板的光照强度从上到下依次为S1=1 000 W/m2、S2=800W/m2、S3=500W/m2,从上到下依次为 T1=30℃、T2=25℃、T3=20℃温度。图3为以上三块单体电池的输出特性曲线P-U、I-U图。

图3 光伏电池板处于非均一光照照射条件下的输出特性I-U、P-U曲线Fig.3 I-U and P-U curves of the output haracteristics of photovoltaic panels under non-uniform illumination conditions
由于每块太阳能电池处于非均匀照射环境,受到的光照强度和温度都不一样,所以太阳能电池的输出P-U曲线不再是单峰曲线而变成多峰曲线,从图3可知P-U曲线存在3个峰值点,每个区间都存在一个峰值点(可能最大值),此时若继续用传统的MPPT控制方法有可能跟踪到一个峰值点之后误以为已经达到全局最大峰值点而放弃继续追踪真正的全局最大功率点。三块太阳能电池板串联工作,由于每块太阳能电池板都处于不同的阴影条件下工作,所以光照和温度不同,但同一块太阳能电池板的工作环境是相同的。当电池工作在第一区间时,由于工作电流在7.802 A到10 A之间,P2和P3两块太阳能电池板的短路电流值达不到工作电流最小值7.802 A而被旁路二极管旁路,只有电池P1在工作;当电池工作在第二区间时,工作电流在4.715 A到7.802 A之间,只有P3的短路电流值达不到工作电流最小值4.715 A而停止工作,其它两块电池正常工作;当电池工作在第三区间时,工作电流在4.715 A到0 A之间,所有电池板都能工作在这个区间,三块电池板都可以正常发电。A、B分别为1、2区间和2、3区间的临界点,区间1电流下降到A点等于区间2短路电流,区间2电流下降到B点等于区间3短路电流。由于在每个不同的工作区间参与工作的太阳能电池板个数不同,所以会出现多个局部最大功率点,每个工作区间的最大峰值点与光伏组串的等效光照强度有着直接关系,工作区间与电池板串联数相互对应。在串联组成的光伏阵列中,有几种处于不同情况的电池板组合,就相对应有几个不同的工作区间与局部光伏最大功率点与其对应。
2 基于光伏功率等效面积分析的全局最大功率点(GMPP)工作区间定位
当光伏阵列受到非均匀照射而产生局部阴影情况下输出的P-U特性曲线中存在多个峰值点,通过多峰MPPT控制方法快速追踪到全局真正的最大功率点成为实现光伏最大功率跟踪的关键。在光照照射均匀的情况下的光伏阵列的最大功率点所对应的电压一般为0.76UOC[16]。但当光伏阵列一旦受到由于光照照射不均匀而产生的局部阴影遮挡时,使其P-U特性曲线产生差异,产生多个局部峰值点,从而需要快速、准确、高效的追踪到全局最大功率点所在的工作区间并且对此区间进行快速、稳定的追踪找到全局最大功率点。
2.1 光伏功率等效面积
在太阳能电池受到非均一光照照射的情况时,光伏组串中各d P/d U稳定区间对应的导数为零的点对应着该工作区间的最大峰值点即该区间最大功率点。设d k=d P/d U为各工作区间对应的导数(各个工作区间的工作电压不同),dk从实际上看与光伏组串的工作电流的息息相关。若除了一个区间导数会跌落为0以外,其它各区间的导数都不会跌落为0,则说明不存在其他局部最大功率点,因此电池未受到阴影遮挡(k:非0自然数,最大取电池板组合数)。
在忽略外界温度影响的情况下的工作区间光伏功率等效面积与其对应的最大功率成线性关系如下式:

Spvk是各个区间的光伏等效面积,Spowerk是各个工作区间的光伏功率等效面积,通过比较每个工作区间的光伏功率等效面积的大小来判断全局最大功率点出现在哪个工作区间。
2.2 最大功率点区间定位分析
太阳能电池在不同阴影(即不同光照强度、温度)环境情况下产生的P-U曲线各不相同,因此其不同情况下的d P/d U-U特性也不相同。图4、图5是太阳能电池在五种不同环境下的P-U输出特性曲线图和d P/d U-U导数特性曲线图。曲线1是光伏组串在标准状况下(光照强度为1 000 W/m2、温度为25℃)的P-U输出曲线;曲线2、3、4、5由于光伏组件所受的阴影情况不同,所以最大功率点所在的区间也不同;每个工作区间的最大峰值点又决定了相应工作区间导数曲线为零的点,所以光伏组串的P-U特性与光伏组串的d P/d U-U导数特性有着直接联系。

图4 五种不同条件下光伏组串P-U曲线Fig.4 P-U curves of photovoltaic cell under five different kinds of conditions

图5 五种不同条件下光伏组串d P/d U-U曲线Fig.5 d P/d U-U curves of photovoltaic cell under five different kinds of conditions


图6 不同情况光伏组串P-U、d P/d U-U曲线特性Fig.6 P-U and d P/d U-U curve characteristics of photovoltaic panels with different conditions
图6(a)、(b)、(c)是分别处在不同环境下的三组太阳能电池,每组电池都是由三块太阳能电池板串联形成的光伏组串,由于每组光伏组串里的三块电池板受到的阴影遮挡情况均不同,所以三组光伏组串的全局最大功率点所在的工作区间也不同,图6(a)、(b)、(c)三组光伏组串的全局最大功率点分别落在区间1、2、3,从以下三图可以分析出局部最大功率点与其相对应的光伏功率等效的面积的关系。图6(a):S1a=280 W/m2,T1a=15℃;S2a=350 W/m2,T2a=20℃;S3a=1 000 W/m2,T3a=25℃;图 6(b):S1b=700 W/m2,T1b=20℃;S2b=300 W/m2,T2b=15℃;S3b=1 000W/m2,T3b=25℃;图6(c):S1c=1 000 W/m2,T1c=25℃;S2c=600 W/m2,T2c=20℃;S3c=500 W/m2,T3c=15℃。
当光伏阵列是由6块电池板串联并且每块电池板都处于不同阴影遮挡情况下,光伏组串的P-U输出特性和d P/d U-U导数特性如图7所示,根据表2数据可以发现全局的最大功率点MPP5依然是在光伏功率等效面积最大的Spower5所在的工作区间5。

表1 图 6(a)、(b)、(c)光伏功率等效面积Tab.1 Photovoltaic power equivalent area of Fig.6(a),(b),(c)
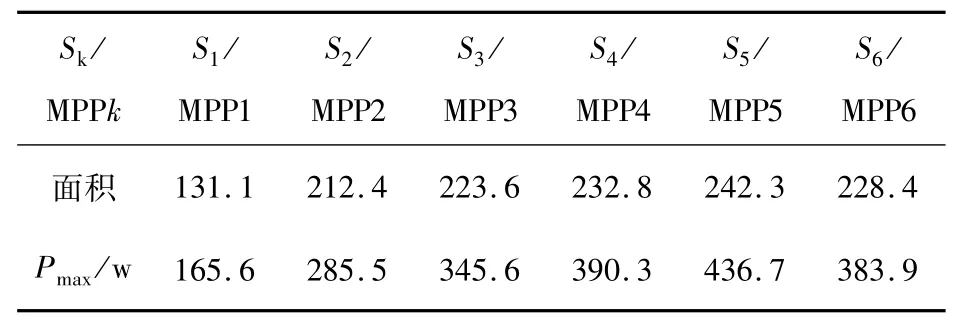
表2 图7光伏功率等效面积Tab.2 PV power equivalent area with Fig.7

图7 处于不同阴影时,6块电池板串联的光伏组串的P-U、d P/d U-U曲线特性Fig.7 P-U and d P/d U-U curves of PV series nnected by 6 panels in series with different shadows
从以上图表可知,在受到局部阴影遮挡时,光伏阵列最大功率点所在的区间与其最大的光伏功率等效面积区间相对应。整个光伏组串的光伏功率等效面积等于各工作区间功率等效面积的总和,可以通过比较各工作区间的光伏功率等效面积来确定光伏组串全局最大功率点所在的工作区间。
3 非均一照射条件下最大功率点追踪仿真及结果分析
3.1 非均一照射条件下最大功率点追踪方法流程图
图8为光伏阵列受到不均匀阴影遮挡时追踪最大功率点流程图。首先需要对d P/d U-U各区间的电流、电压进行采样,计算各区间的导数dk,若只有某一个区间会有导数跌落为0,其他区间导数都不会跌落为0,则说明光伏组件处在均一的光照条件下不存在局部最大功率点,此时就可以使用一般的单峰MPPT控制方法;相反,若存在多个区间导数跌落为0,则说明光伏组件受到局部阴影遮挡,此时需要计算各区间光伏功率等效面积并且找到最大的光伏功率等效面积所在的区间,全局最大功率点定位在此工作区间,最后在所确定的工作区间采用一般的MPPT控制方法对全局最大功率点进行快速跟踪。

图8 非均一照射条件下最大功率点追踪方法流程图Fig.8 Flow chart of maximum power point tracking method under non-uniform illumination
3.2 基于光伏功率等效面积法的全局最大功率点追踪仿真结果及分析
图9为两块太阳能电池板串联的光伏组串的P-U输出特性和d P/d U-U导数特性,太阳能电池的相关参数:ISC=9.2、UOC=34.2、Im=7.95、Um=20、a=0.002 5℃、b=0.002 5℃、c=0.002 88℃;S1=1 000W/m2,T1=25℃;S2=600W/m2,T2=20℃。

图9 非均一光照条件下,两块电池板串联的光伏组串的P-U、d P/d U-U曲线特性Fig.9 P-U and d P/d U-U curves of PV series connected by two panels in series under shadow
将上述光伏组串的相关特性的数据导入MATLAB中的LookUp模块来模拟受到不均匀阴影遮挡的光伏组串,并且采用本文所提出的光伏功率等效面积法来追踪光伏系统全局最大功率点。图10为在受到非均一光照照射条件时采用光伏功率等效面积法追踪全局最大功率点的光伏系统模型仿真图,其中系统所采用的直流-直流变换器是由状态方程建立的boost变换器,相关参量选择:电感:6mH;等效电阻:0.1Ω;DC电容:45μF;负载电阻:16Ω。MPPT模块里采用的是电导增量法的改进法—基于Newton-Raphson法快速计算光伏系统d P/d U的微分值,通过分析d P/d U的值是否为0或者大于0以及小于0来快速改变系统占空比调节系统在工作时的最大功率点所对应的参考电压,此方法追踪速度优于传统的MPPT控制方法,能够快速、准确的追踪到全局最大功率点。

图10 非均一光照条件下,系统仿真图Fig.10 System simulation diagram under non-uniform illumination

图11 占空比曲线Fig.11 Duty ratio curve

图13 P-I曲线(功率-电流曲线)Fig.13 P-I curve(power-current curve)

图14 U-I曲线(电压-电流曲线)Fig.14 U-I curve(voltage-current curve)
从图11~图14系统仿真结果图中可以看出本文所采用的光伏功率等效面积法可以快速、有效、准确的跟踪到系统全局最大功率点,从系统开始工作到0.022 s之间boost的占空比在第二个工作区间大幅度的震荡变化,在0.022 s之后光伏系统的电压和电流分别稳定在45.8 V和4.83 A,最大功率点稳定在221.3 W,光伏系统也稳定的维持在该功率点工作,此结果证明了光伏功率等效面积法的正确性。
4 结束语
由于非均匀照射而产生的局部阴影,使得整个光伏组串的P-U曲线出现了多个峰值点,因此追踪单一峰值点的常规MPPT控制算法失去效用,必须研究针对追踪多个峰值点的MPPT控制方法。在分析光伏组串的d P/d U-U导数特性的基础上提出了光伏功率等效面积法—通过光伏组串的导数特性寻找到最大光伏功率等效面积所在工作区间即全局最大功率点所在区间,再对此工作区间采用追踪单一峰值的MPPT控制方法追踪全局最大功率点。为验证此方法正确性,利用Matlab软件搭建了非均一光照条件影响下的光伏组串仿真模型,采用光伏功率等效面积法对系统进行最大功率跟踪。仿真实验结果说明所提出的基于光伏功率等效面积法的多峰MPPT控制方在跟踪速度、准确度以及平稳度方面效果良好,验证了光伏功率等效面积法的正确性以及有效性。
