矢量Kirchhoff叠前深度偏移

2017-12-18荣骏召李建峰王成祥

石油地球物理勘探 2017年6期

关键词：标量积分法波场

荣骏召芦俊* 李建峰王成祥

(①中国地质大学(北京)能源学院，北京 100083； ②东方地球物理公司物探技术研究中心，河北涿州 072751)

·偏移成像·

矢量Kirchhoff叠前深度偏移

荣骏召①芦俊*①李建峰②王成祥②

(①中国地质大学(北京)能源学院，北京 100083； ②东方地球物理公司物探技术研究中心，河北涿州 072751)

由于传统的Kirchhoff积分法偏移基于标量声学波动方程，没有考虑地震波场的矢量特性，偏移成像的精度较低、保幅性较差。因此，本文从多分量地震波矢量场的特征出发，基于均匀各向同性弹性波波动方程，推导了Kirchhoff积分法矢量偏移公式；利用弹性波波动方程的矢量特性，在偏移过程中将泄漏的地震波信息还原到PP波与PS波分量中，实现了偏移过程中的波场分离。二维理论模型与实际数据的应用结果表明，基于矢量数据的深度偏移方法能够有效消除多分量地震数据的波型泄漏现象，提高偏移成像的精度。

叠前深度偏移 Kirchhoff积分法偏移矢量多分量

1 引言

在多分量地震勘探的实验阶段常常假设垂直分量主要接收PP波，水平分量主要接收PSV波和PSH波，但这种假设的前提条件是近地表存在低速带，地震波近似垂直出射地表。但实际上，随炮检距的增大，尤其近地表存在高速层时，地震波几乎无法垂直出射，这会导致地震波偏振矢量与检波器的三个分量之间存在夹角。因此，三分量检波器的每一个分量都会同时接收纵横波的部分投影，即出现“波型泄漏”现象[1-5]。

传统的声波方程为解决波型泄漏问题，通常会进行波场分离，主要采用波数域滤波及Radon变换等[6-8]。但波数域滤波很容易丢失地震数据的低频成分，Radon变换通常会存在保幅性差的问题[9-11]。为此，人们对波场分离方法进行了研究。郭鹏等[12]根据地震波偏振方向，提出了空间域VTI介质弹性波波场分离方法；薛亚茹等[13]提出了高阶高分辨率Radon变换方法，很大程度上解决了保幅性问题；魏石磊等[14]对VTI介质中波场分离算子的特征进行了更深入的研究。但这些方法分离得到的qP波和qPS波通常是获得了两种波在z方向和x方向上的投影，没有将泄漏的地震波信息恢复到各自的分量中。

若要在偏移成像中解决波型泄漏问题，做到真正的纵横波波场分离，就需要考虑地震波传播的矢量特性。弹性波波动方程能够模拟弹性介质中纵波和横波的传播特征，更接近于真实的地震波传播。对原始弹性波波场求取散度和旋度，可得到原始波场的标量势和矢量势，完成波场分离，这是矢量法解决波型泄漏问题的基本思路[15，16]。因此，叠前偏移方法需要从标量的声波波动方程向矢量的弹性波波动方程发展。Kuo等[17]给出了弹性波波场延拓方程，并在Pao等[18]推导出的弹性波Kirchhoff-Helmholtz积分形式的基础上，进行了波场分离、偏移成像，实现了偏移过程中的波场分离；秦福浩等[19]在此基础上引入矢量偏移的概念，并推导出了弹性波矢量Kirchhoff积分形式。

本文在秦福浩等[19]的弹性波矢量Kirchhoff积分形式的基础上，进一步推导了二维多分量地震数据PP波与PS波的矢量Kirchhoff偏移公式。该公式利用弹性波波动方程的矢量特性，在偏移过程中将泄漏的地震波信息还原到PP波与PS波分量中，实现偏移过程中的波场分离。

2 矢量Kirchhoff叠前深度偏移

2.1 方法原理

图1为半封闭自由空间示意图。S′是空间表面，n(x)是S′的法向量。根据Kirchhoff-Helmholtz积分方程，指向自由空间的位移矢量场u(x)在弹性介质中的波动方程为[18]

(1)

式中F为牵引向量，可以表示为

(2)

而应力张量T又可以表示为

(3)

图1 半封闭自由空间示意图

Kuo等[17]给出了均匀各向同性介质中三维矢量波波场向下延拓的方程

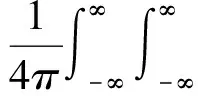
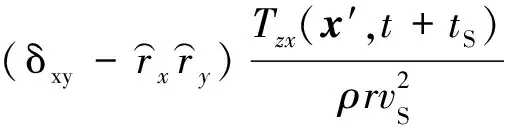
(4)

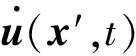
对于自由表面边界条件，地表应力为0，式(4)的后两项可以舍去[18]，有

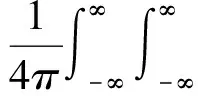
(5)

图2 矢量在空间坐标上的投影

将式(5)展开，并将两个分量上的能量分别投影到PP波分量和PS波分量(二维数据时PS波分量特指PSV波分量)上，如图2所示，有

UPP=U1cosθsinφ+U2sinθsinφ+U3cosφ

(6)

UPS=U1cosθcosφ+U2sinθcosφ+U3sinφ

(7)

通过该方法，可以将波型泄漏部分的能量重新恢复到原来的分量中，确保地震波振幅信息得到准确的还原，同时消除各分量在成像时的相互干扰。

将式(5)展开后代入式(6)、式(7)，得

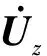
(8)

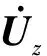
(9)

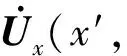
在二维多分量勘探中通常使用涨缩震源，因此理论地震记录上只存在PP波和PSV波。若令垂向为z轴方向，测线方向为x轴方向，则y分量上无波场信息，则可将式(8)、式(9)简化为二维弹性波Kirchhoff积分法矢量偏移公式

(10)

(11)

2.2 PP波与PS波联合成像步骤

本文方法同时输入z分量与x分量完成联合成像，并没有单分量单独成像,原因是在偏移前不需要进行波场分离，保留了各分量中的波型泄漏信息，在联合成像的过程中，依据地震记录的矢量特性完成波场分离，最大程度地恢复地震波的振幅信息。

Kirchhoff积分法矢量偏移公式在偏移过程中实现了PP波与PS波的波场分离，将z分量与x分量中的PP波与PS波信息分别偏移叠加，具体流程如下：

(1)输入纵、横波速度模型，通过射线追踪计算每个成像点的纵波一次反射走时tP和横波一次反射走时tS、出射角(θP、θS)及纵横波射线路径(lP、lS)，如图3所示；

(2)将偏移所需的地震数据读入内存空间，包括道头信息及地震道信息；

(3)对成像点进行循环，依次读取成像点的纵波和横波走时、出射角，以此计算纵波和转换波的走时(t+tP,t+tS)，然后根据式(10)、式(11)，将z分量与x分量中的PP波、PS波数据分离累加到UPP和UPS中；

(4)完成对成像点的循环后分别输出纵波剖面与转换波剖面。

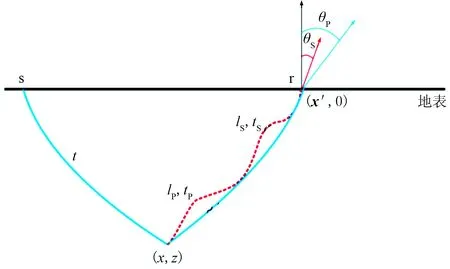
图3 射线追踪示意图

3 模型数据试验

为了证明该方法的有效性，首先用模型数据对方法进行了测试，设计的二维模型如图4所示。模型尺寸为1000m×1000m，共有5层介质、4个反射界面，每层介质的参数见表1。由于模型的第2和第3个反射界面构造形态复杂，合成记录中反射波、绕射波等波之间出现相切连接、斜交干涉等现象(图5)，导致地震波波场矢量信息变得更加复杂。因此该模型能够很好地检验矢量Kirchhoff偏移方法解决波型泄漏问题的能力。

表1 模型参数

本文采用弹性波有限差分正演方法，建立的观测系统如下：道间距为5m，5炮，每炮200道，初始炮点坐标x=100m，炮间距Δx=200m；采样间隔为0.5ms，采样点数为2401。对比z分量、x分量的第3炮炮集记录，如图5中箭头所示，z分量中有PS波泄漏部分，x分量中有PP波泄漏部分。由此可以证明，波型泄漏确实存在。

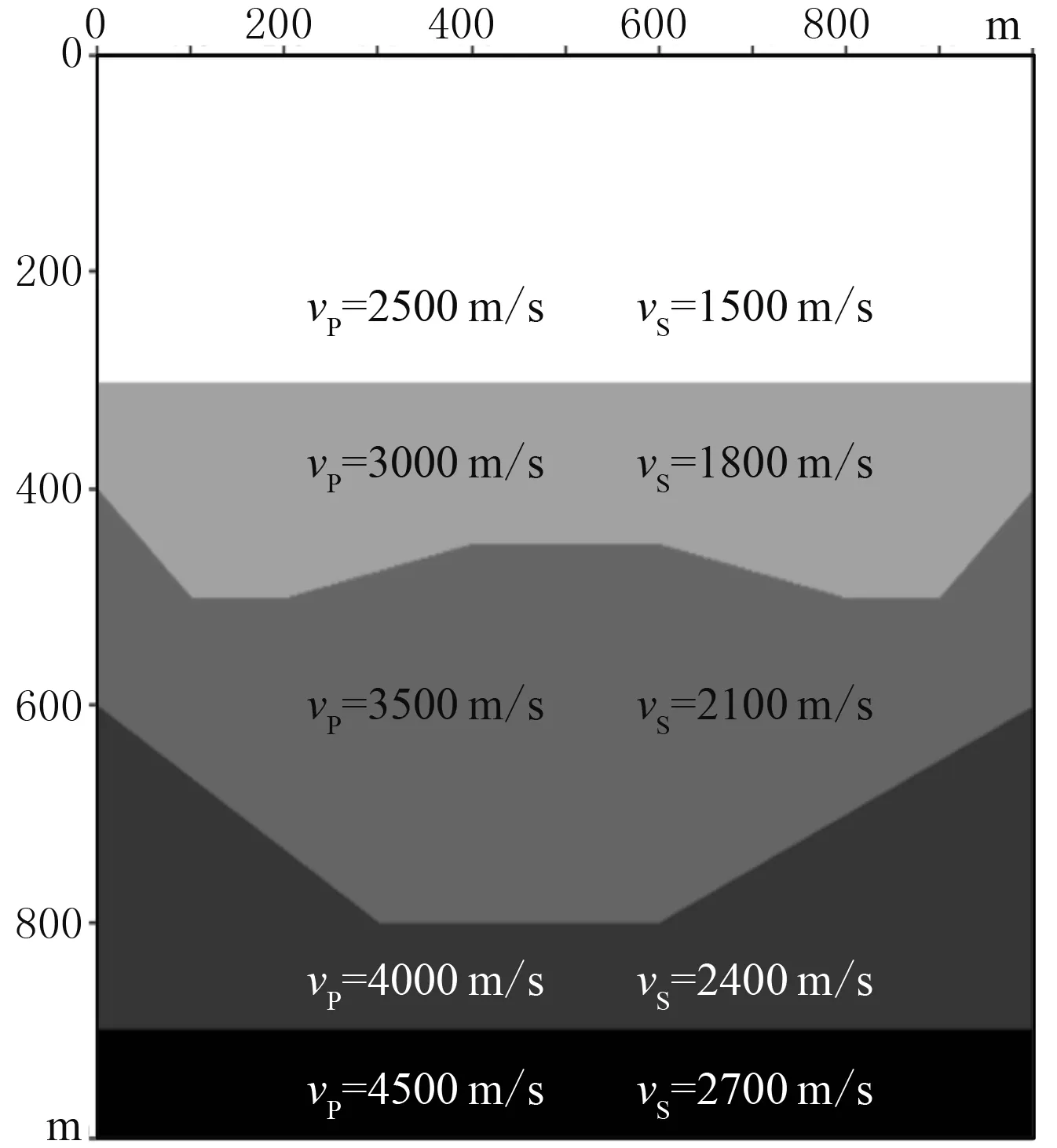
图4 二维速度模型

先用文中方法对两分量合成记录做偏移，得到的PP波剖面和PS波剖面如图6所示。随后，又运用标量Kirchhoff偏移方程对该合成记录做偏移成像，得到的PP波剖面与PS波剖面如图7所示。

对比图6和图7可以看出，矢量偏移的PP波分量剖面中减少了大部分PSV波的干扰，PSV波分量剖面中的大部分PP波信息也同样被还原。这表明本文的矢量偏移方法在波场标定、消除波型泄漏方面达到了预期效果。同时相比于标量Kirchhoff积分法偏移，弹性波矢量偏移方法提高了剖面的成像精度。

图5 第3炮单炮合成记录

图6 矢量偏移剖面

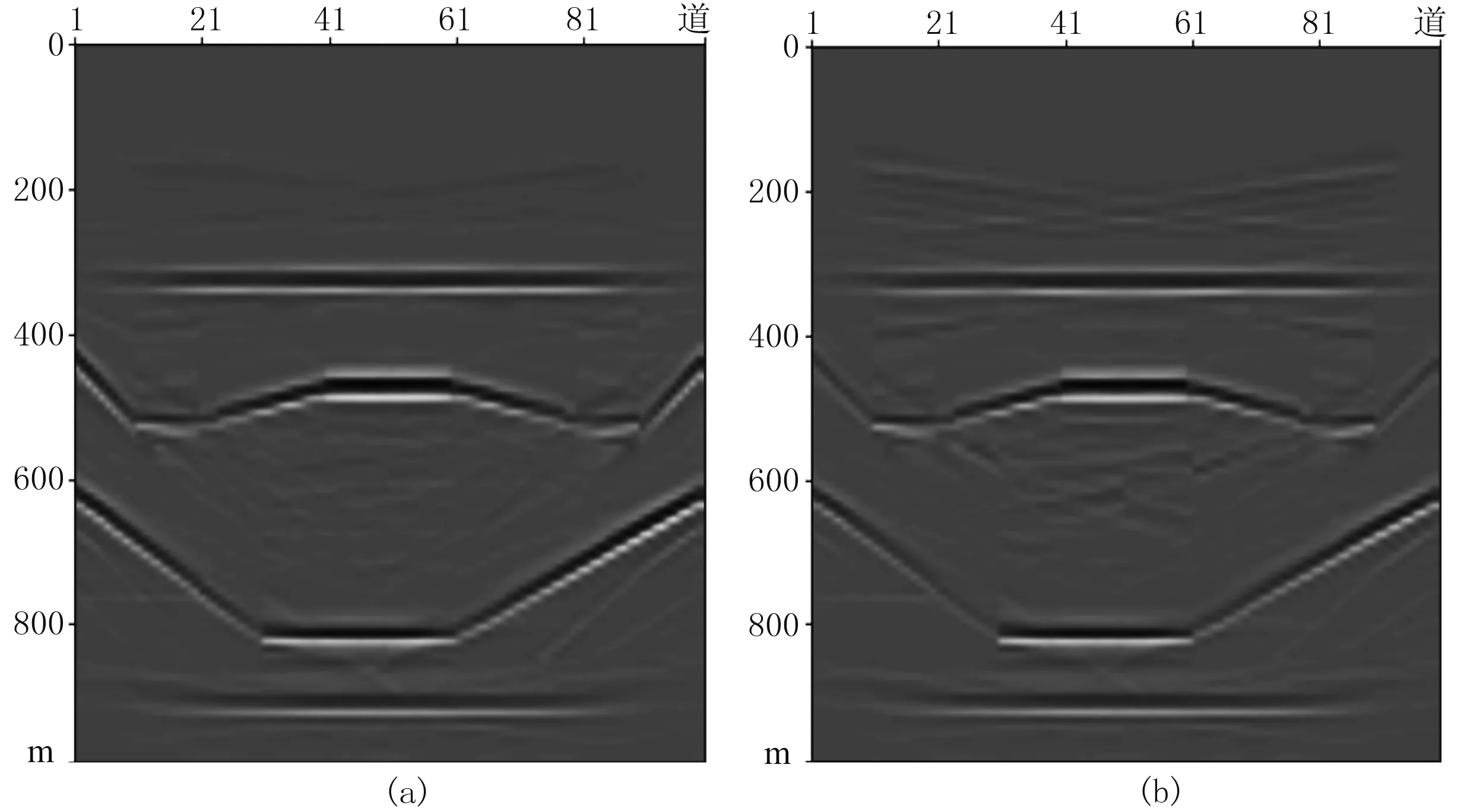
图7 标量Kirchhoff积分法偏移剖面

4 实际数据处理

实际数据测试采用大庆油田采集的汪家屯地区的二维三分量地震数据[20]。工区位于松辽盆地北部某深层断陷区，地下构造复杂、火成岩发育，火山岩储层是该区深层气藏勘探的主要储层类型。为加强对构造、岩性、裂缝的各向异性研究，深入认识火山岩气藏的富集成藏规律，在该区进行了二维三分量地震勘探试验。图8为野外采集的x分量、z分量单炮记录。

分别使用标量Kirchhoff积分法偏移和矢量Kirchhoff积分法偏移方程对两分量数据进行偏移成像，得到的偏移剖面分别如图9、图10所示。可以看出，两种偏移方法得到的纵波剖面在浅层(2000m以上)的成像精度相差较小，原因是2000m以上地层对应构造稳定的陆相沉积[21]，地震波波场矢量特征相对较简单，波型泄漏现象较深层并不明显。但矢量法得到的转换波剖面在1500m位置对小断层的刻画比标量法精细得多(图10b)。同样，矢量法纵波剖面在2000m位置对断层的分布及断点位置的成像也优于标量法得到的偏移剖面。

矢量法的优势是在于对地下复杂构造的成像。由于标量法无法分析地震波波场矢量信息，所以对2000m以下的复杂构造区域成像精度低，3500m深度的目标火成岩储层刻画十分模糊(图9)。由矢量法偏移剖面(图10)可以看出，其纵波及转换波剖面在深层(2000m)的分辨率明显高于标量法剖面，而且对3500m深度处的火成岩储层构造刻画更为精细。矢量法剖面深层成像质量提高的原因是分离了原z分量、x分量中的PS波和PP波信息，并将这些有用信息补偿到各自的偏移剖面中，提高了成像剖面的分辨率以及成像精度。

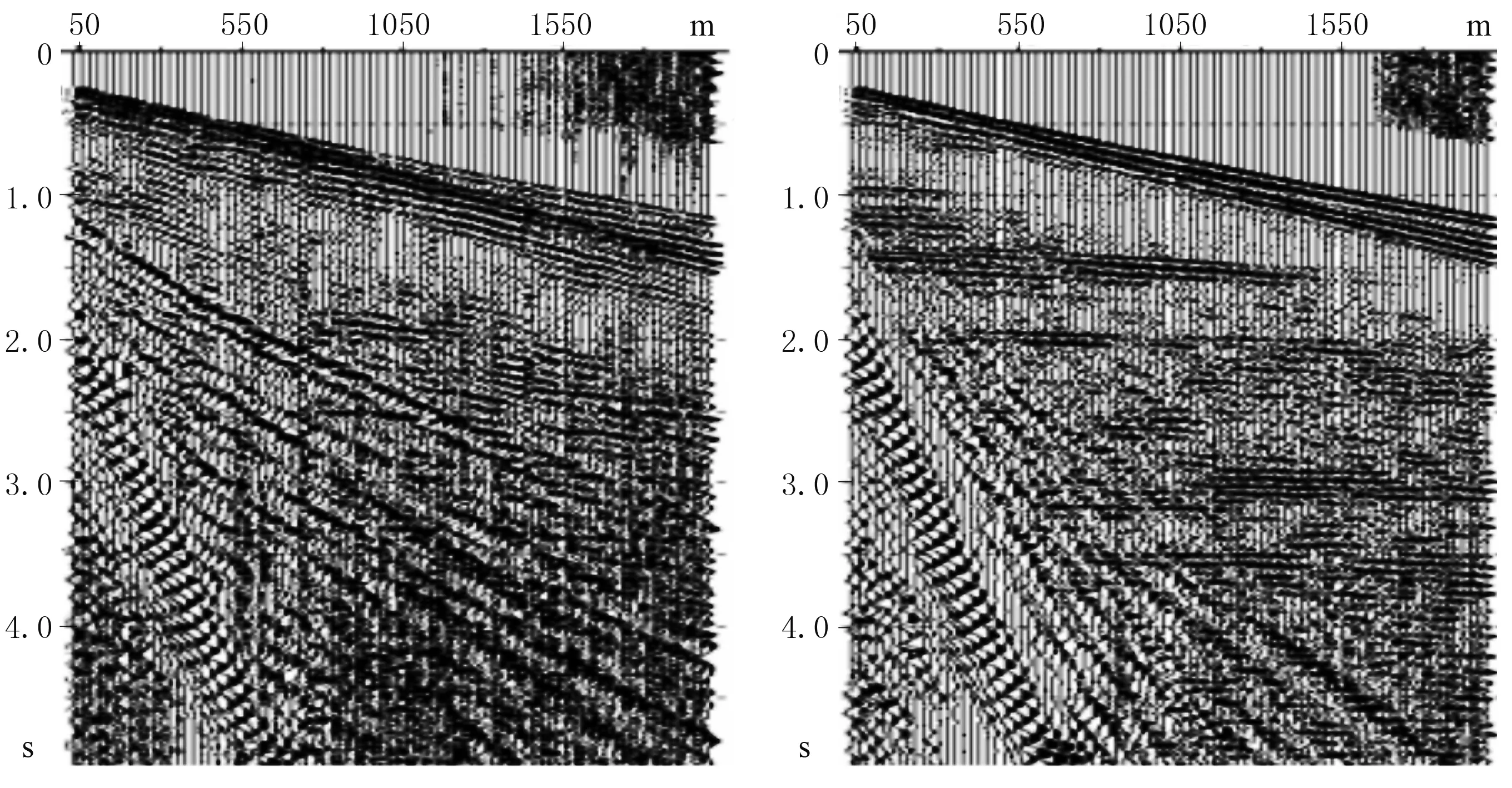
图8 x分量(左)及z分量(右)单炮记录

图9 标量Kirchhoff积分法叠前深度偏移剖面

图10 矢量Kirchhoff积分法叠前深度偏移剖面

5 结论与讨论

(1)矢量Kirchhoff积分法偏移基于矢量场波动方程，可以将两分量中的PP波与PS波通过矢量分解的方法分别投影到PP波与PS波分量上，消除了多分量地震数据的波型泄漏现象。矢量方法的最大意义不只是恢复了振幅信息，同时还在很大程度上消除了其余分量地震信息的干扰。因此，使用该方法得到的偏移剖面构造刻画更加精细，分辨率也得到提高，更能满足实际地震勘探的需要。

(2)本文方法根据纵横波速度模型计算出地震波的走时、出射角度和射线路径，然后遍历成像点，提取不同成像点的矢量信息完成矢量偏移。因此，该方法对速度模型的精度要求较高。

(3)本文推导出的矢量Kirchhoff偏移方程只针对二维多分量地震数据，暂时还无法完成三维多分量数据的矢量偏移成像。三维地震波波场更加复杂，因此完成其矢量偏移意义重大。如何正确分解三维地震波矢量，如何完善弹性波三维矢量Kirchhoff偏移方程是未来要解决的问题。同时，模型数据的矢量偏移结果表明，目前的矢量方法并未完全消除波型泄漏问题，如何改进波矢量分解，进一步提高成像质量将是一个很重要的课题。

本文研究得到了中国地质大学(北京)王赟教授和CGG公司英国技术中心侯嵩博士的大力支持，在此表示感谢。

[1] Lu J,Wang Y and Yao C.Separating P-and S-waves in an affine coordinate system.Journal of Geophysics and Engineering,2012,9(1):12-18.

[2] Dellinger J and Etgen J.Wave-field separation in two-dimensional anisotropic media.Geophysics,1990,55(7):914-919.

[3] Yan J,Sava P.3D elastic wave mode separation for TTI media.SEG Technical Program Expanded Abstracts,2009,28:4292-4298.

[4] Wang Zhiyang,Liu Hong.Separation of elastic wave mode based on improved interpolation algorithm.Near-Surface Asia Pacific Conference,Waikoloa,Hawaii,2015:108-112.

[5] Lou M,Campbell M,Cheng D et al.An improved para-metric inversion methodology to separate P and SV wavefields from VSP data.SEG Technical Program Expanded Abstracts,2013，32:5087-5091.

[6] 马见青,李庆春.利用时频域极化滤波压制地震面波.石油地球物理勘探,2015,50(6):1089-1097.

Ma Jianqing,Li Qingchun.Seismic surface wave suppression with polarization filtering method in time-frequency domain.OGP,2015,50(6):1089-1097.

[7] 程冰洁,胡治权,徐天吉等.小波域能量分类约束极化滤波法及应用.石油地球物理勘探，2015,50(5)：815-823.

Cheng Bingjie,Hu Zhiquan,Xu Tianji et al.Polarization filtering constrained by classified energy in the wavelet domain.OGP,2015,50(5):815-823.

[8] 何银娟,李稳,刘保金等.改进的矢量分解压噪方.石油地球物理勘探,2015,50(2):243-253.

He Yinjuan,Li Wen,Liu Baojin et al.An improved vector resolution noise removal approach.OGP,2015,50(2):243-253.

[9] Foster D J,Mosher C C.Suppression of multiple reflections using the Radon Transform.Geophysics,1992,57(3):386-395.

[10] Zhou B,Greeenhalgh S A.Linear and parabolic transform.Geophysics,1994,59(7):1133-1149.

[11] 黄新武,吴律,宋炜.拉东投影法三维叠前深度偏移.地球物理学报,2004,47(2):321-326.

Huang Xinwu,Wu Lü,Song Wei.3-D pre-stack depth migration with Radon projection.Chinese Journal of Geophysics,2004,47(2):321-326.

[12] 郭鹏,何兵寿,沈骥千.VTI介质弹性波波场分解的空间域算法.石油地球物理勘探,2013,48(4):567-575.

Guo Peng,He Bingshou,Shen Jiqian.Space domain algorithm of elastic wave-field decomposition in VTI media.OGP,2013,48(4):567-575.

[13] 薛亚茹,唐欢欢,陈小宏.高阶高分辨率Radon变换地震数据重建方法.石油地球物理勘探,2014,49(1):95-100.

Xue Yaru,Tang Huanhuan,Chen Xiaohong.Seismic data reconstruction based on high order high resolution Radon transform.OGP,2014,49(1):95-100.

[14] 魏石磊,张大洲,李明智等.VTI介质中波场分离算子特征研究.石油地球物理勘探,2016,51(3):506-512.

Wei Shilei,Zhang Dazhou,Li Mingzhi et al.Wave field separation operator characteristics in the VTI media.OGP,2016,51(3):506-512

[15] 杜启振,秦童.横向各向同性介质弹性波多分量叠前逆时偏移.地球物理学报,2009,52(3):801-807.

Du Qizhen,Qin Tong.Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic medium.Chinese Journal of Geophysics,2009,52(3):801-807.

[16] 李振春,雍鹏,黄建平等.基于矢量波场分离弹性波逆时偏移成像.中国石油大学学报(自然科学版),2016,40(1):42-48.

Li Zhenchun,Yong Peng,Huang Jianping et al.Elastic wave reverse time migration based on vector wavefield separation.Journal of China University of Petroleum (Edition of Natural Science),2016,40(1):42-48.

[17] Kuo J T,Dai Tingfan.Kirchhoff elastic wave migration for the case of noncoincident source and receiver.Geophysics,1984,49(8):1223-1238.

[18] Pao Y H,Vararharajulu V.Huygens’ principle radiation conditions and integral formulas for the scattering of elastic waves.Journal of the Acoustical Society of America,1976,59(6):1361-1371.

[19] 秦福浩,郭亚曦,王妙月.弹性波克希霍夫积分偏移法.地球物理学报,1988,31(5):577-587.

Qin Fuhao,Guo Yaxi,Wang Miaoyue.The Kirchhoff elastic wave migration method.Chinese Journal of Geo-physics,1988,31(5):577-587.

[20] 舒萍,门广田,刘启.汪家屯气田地质再认识与开发动态分析.天然气工业,2004,24(9):108-112.

Shu Ping,Men Guangtian,Liu Qi.Re-recognize geology of Wangjiatun gas field and analyze producing performance.Natural Gas Industry,2004,24(9):108-112.

*北京市海淀区学院路29号中国地质大学(北京)能源学院，100083。Email:lujun615@163.com

本文于2016年12月16日收到，最终修改稿于2017年8月23日收到。

本文研究受国家自然科学基金项目(41604119、41425017、41374131、41574126、41504107)和中国石油天然气集团公司“弹性波地震成像技术合作研发”项目联合资助。

1000-7210(2017)06-1170-07

荣骏召，芦俊，李建峰，王成祥.矢量Kirchhoff叠前深度偏移.石油地球物理勘探，2017,52(6):1170-1176.

P631

10.13810/j.cnki.issn.1000-7210.2017.06.006

(本文编辑：金文昱)