瑞雷波有限差分数值模拟中不同自由表面边界条件的对比

2017-12-18袁士川宋先海

石油地球物理勘探 2017年6期

关键词：雷波剖分镜像

袁士川宋先海*② 蔡伟胡莹鲁鹏

(①中国地质大学地球物理与空间信息学院，湖北武汉 430074； ②地球内部多尺度成像湖北省重点实验室，湖北武汉 430074)

·地震模拟·

瑞雷波有限差分数值模拟中不同自由表面边界条件的对比

袁士川①宋先海*①②蔡伟①胡莹①鲁鹏①

(①中国地质大学地球物理与空间信息学院，湖北武汉 430074； ②地球内部多尺度成像湖北省重点实验室，湖北武汉 430074)

自由表面边界条件是决定瑞雷波数值模拟效果的关键因素。本文基于标准交错网格高阶有限差分法，在二维各向同性弹性介质背景下，针对应力镜像法(SIM)、改进应力镜像法(MSIM)、横向各向同性介质替换法(MS)和声学—弹性边界近似法(AEA)等四种最具代表性的自由表面边界条件进行了数值模拟，并在均匀半空间模型中从波场快照、波形曲线和频散曲线三个角度进行了对比分析。在相同条件下，上述四种方法均能生成符合勘探地球物理规律的波场快照，各自对应的数值解与解析解的拟合误差都随网格剖分精度的提高而减小，SIM和AEA数值模拟的稳定性和精度都明显高于MSIM和MS。基于层状介质模型的进一步研究表明：对于简单模型，SIM和AEA都能得到比MSIM和MS更高精度的数值模拟结果；对于复杂模型，AEA的精度最高，是最适合瑞雷波数值模拟的自由表面边界条件。

瑞雷波有限差分模拟自由表面边界条件应力镜像法声学—弹性边界近似法

1 引言

在石油勘探、浅层反射及折射波人工地震勘探中，瑞雷波是一种强干扰波；在天然地震中，瑞雷波是危害性最大的一种地震波。因此，在早期研究中，人们主要是根据瑞雷波的特点，采取诸多方法消除其影响或减小其危害。但当人们发现瑞雷波在层状介质中具有频散特性后，就逐渐将其作为有效波并充分利用该特性研究各种地球物理问题。所谓频散特性，是指瑞雷波相速度随频率变化，而此特性主要与地层中纵、横波速度、密度及厚度有关，尤其对横波速度和厚度敏感，因此有人提出了通过反演瑞雷波相速度获取横波速度和厚度的方法[1]。浅地表最关键的地震参数是横波速度，故该方法在岩土分层、场地原位测试、工程质量无损检测和地震安全评价等浅地表结构探测中得到广泛应用，其中最具代表性的是瑞雷波多道分析法(Multichannel Analysis of Surface Waves，MASW)[2]。

瑞雷波多道分析法通过反演瑞雷波相速度获得浅地表的剪切波速度结构，而真实的浅地表地质环境非常复杂，通过地震波场数值模拟技术研究典型的浅地表地质模型，对提高实测资料采集质量与反演解释精度等都具有重要作用。数值模拟方法有很多种类，而有限差分法以其计算速度快、占用内存小、能模拟复杂介质等优点，在地震波场数值模拟中已得到广泛应用。例如：董良国等[3]研究了一阶弹性波方程交错网格高阶差分解法，并对其稳定性进行了分析；周竹生等[4]利用有限差分算法实现了弹性介质瑞雷波正演模拟；熊章强等[5]基于瑞雷波数值模拟实例分析了差分阶数和网格剖分精度对计算效率的影响；邵广周等[6]通过数值模拟对瑞雷波频散曲线特征及各模式能量分布进行了详细分析；李振春等[7]提出了变网格差分算法，在兼顾计算成本的同时提高了对复杂介质的刻画精度；杜启振等[8]基于优化差分系数法实现了横向各向同性介质地震波场数值模拟。此外，考虑到实际地质环境的复杂性，业界也对起伏地表、黏弹性和含孔隙性等也做了数值模拟研究[9-14]。由于瑞雷波是纵波(P波)和横波(SV波)在自由表面处相长干涉而形成的沿自由表面传播的特殊地震波，因此与体波相比，其波场数值模拟实现起来更困难，且对自由表面边界条件有更高要求。如何处理自由表面问题，将直接影响瑞雷波数值模拟效果。此前，已对适用于有限差分的自由表面边界条件做了卓有成效的研究，这些成果可粗略地分为均匀介质法和非均匀介质法[15]两大类。

均匀介质自由表面处理方法是指基于波动方程、通过在自由表面上直接设置应力连续性条件而实现自由边界处理的方法。Aki等[16]最早给出垂直自由表面应力为零的自由表面边界条件理论表达式，但该式在离散波动方程求解过程中实现困难。为此，Levander[17]提出了应用镜像技术近似处理弹性自由表面的方法。随后在对于自由表面以上虚拟层中速度分量的处理问题上出现了分歧，出现了三种不同处理方式[17-19]。Robertsson[18]对比了这三种方式，指出在虚拟层中速度分量设置为零的镜像处理方式最好，也就是现在使用最为广泛的应力镜像法(Stress Image Method，SIM)；同时，还指出Hestholm等[20]使用直接法[21]处理自由表面是不稳定且精度较低的。王秀明等[22]基于常规应力镜像法，提出一种新的自由表面处理方法，称之为改进应力镜像法(Modified Stress Image Method，MSIM)，该方法改变了自由表面在差分网格中的采样位置，并使自由边界条件的设置更加简单。

非均匀介质自由表面处理方法是指在自由表面上，通过调整弹性参数分布间接地实现自由边界处理的方法。这种思想最早由Boore[23]提出，之后经过众多研究与应用，发展了几种不同的处理方式。真空法较早被提出，它是通过在自由表面以上网格中设置拉梅常数为零和密度接近零的方法处理自由边界，因其实现过程简单，故被广泛使用[24，25]。Mittet[26]提出另一种被称为“横向各向同性介质替换法”或“Mittet's Scheme(简称为MS)”的非均匀介质自由表面处理方法。与真空法相比，MS对拉梅常数和密度进行了更细致的处理，使数值模拟的精度得到了提高。Xu等[27]考虑了自由表面上下横向应力保持连续的条件，提出了用声学—弹性介质边界近似代替自由表面的处理方式，被称作“声学—弹性边界近似法(Acoustic-elastic Boundary Approach，AEA)”。

不同自由表面处理方法的处理效果和精度存在差异。将多种方法做对比研究，对于瑞雷波和其他地震波场模拟研究都具有重要意义。Graves[25]通过数值模拟指出应力镜像法比真空法具有更高精度； Bolhen等[15]对比了应力镜像法与横向各向同性介质替换法后，认为应力镜像法的精度更高； Xu等[27]将应力镜像法、横向各向同性介质替换法、真空法及声学—弹性边界近似法进行了对比，指出声学—弹性边界近似法能达到与应力镜像法相当的精度，而真空法精度最低；王周等[28]对直接法、应力镜像法、改进应力镜像法、横向各向同性介质替换法及声学—弹性边界近似法进行了对比研究，认为横向各向同性介质替换法的精度和可靠性最高。可见：一方面现有的对比研究还欠充分、全面；另一方面各自结论不统一，且基本上只从均匀半空间波形曲线角度进行对比。然而，瑞雷波波场数值模拟不仅具有波形曲线解析解，还存在频散曲线解析解。波形曲线只利用了单道地震记录信息；而频散曲线则综合考虑了多道地震记录信息，消除了瑞雷波近场效应和远场效应影响。“频散”是瑞雷波最重要的特性，故从频散曲线角度进行对比很有必要。此外，从波场快照可直观地分析瑞雷波传播特性，故波场快照也是可选的对比“角度”。因此，从多方面综合考虑，全面对比、评估各种自由表面边界条件的数值模拟精度和稳定性，才可得出更可靠结论。

鉴于此，本文在上述研究基础上，利用标准交错网格高阶有限差分算法，针对二维各向同性弹性介质，在均匀半空间、两层速度递增、三层含低速软夹层及四层含高速硬夹层等四种典型地质模型中，从波场快照、波形曲线和频散曲线三个“角度”对(应力镜像法、改进应力镜像法、横向各向同性介质替换法、声学—弹性边界近似法等)四种最具代表性的自由表面处理方法，进行了定性—定量、综合的数值模拟对比研究，以期为瑞雷波和其他地震波场模拟研究提供科学和有价值的参考。

2 理论依据

本文采用各向同性介质一阶速度—应力弹性波方程进行有限差分数值模拟。对于二维P-SV波 (xoz平面)，其差分形式可表示为[27]

(1)

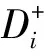
(2)

自由表面是固体地球与空气层之间的物性突变面，瑞雷波正是基于它的存在才得以形成和传播。Aki等[16]最早给出垂直自由表面应力为零时的自由表面边界条件，二维水平自由表面(z=0)处的表达式为

(3)

该式在理论上非常简单，而在离散波动方程求解过程中却难以实现，且空间差分阶数越高，处理越困难。但重要的是，它为后续各种自由表面处理方法，提供了思想基础。下面将详细介绍用于对比的四种自由表面边界条件的基本原理及其设置方法。

2.1 应力镜像法

应力镜像法[18]的基本思想是把自由表面看作一面镜子，在镜面之上设置虚拟层，并使上、下两侧与垂向相关的应力(σzz、σxz)关于自由表面镜像对称，虚拟层中速度分量设置为零。在二维交错网格中，SIM认为自由表面通过正应力σxx、σzz和速度水平分量vx的采样位置，即自由表面位于整数网格线(粗线)上。如图1所示，i和j分别为横向和纵向网格剖分点，j也表示自由表面所在位置，蓝色正方形表示σxx和σzz，蓝色圆形表示σxz，绿色倒三角形表示vz，绿色正三角形表示vx。

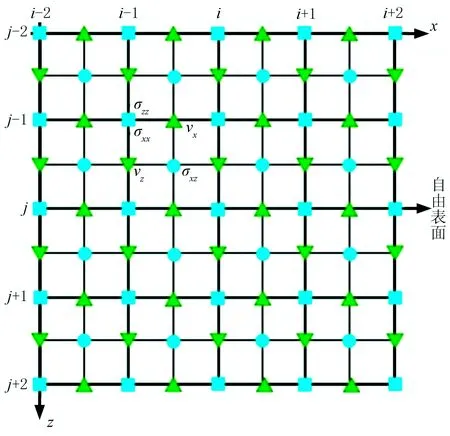
图1 应力镜像法自由表面取样位置

在2L阶标准交错网格有限差分条件下，虚拟层宽度为L个网格点，则应力设置方式为

(4)

式中k(=1,2，…，L)为虚拟层中正参与镜像处理的网格点距离自由表面的网格点数。式(4)中正应力和切应力在边界上都是奇函数，保证它们在边界上为零。

同时，在自由表面上，正应力σxx采用下式(据式(3))进行迭代

(5)

利用该式进行迭代可使数值模拟更加稳健。

2.2 改进应力镜像法

改进应力镜像法[22](MSIM)与SIM的不同之处在于，在二维交错网格中，MSIM认为自由表面是通过切应力σxz和速度垂直分量vz的采样位置，即自由表面位于半网格线上(图2中细线)。

图2 改进应力镜像法自由表面取样位置

在2L阶标准交错网格有限差分条件下，虚拟层具有L个网格点宽度，其应力设置方式为

(6)

与SIM相比，MSIM具有两大优点[22]： ①由于正应力σxx、σzz不在自由表面上采样，因此不需单独对σxx做式(5)的处理，直接采用式(6)就能满足条件； ②当边界形状构成一个顶角时，SIM需正应力σxx、σzz为零，而MSIM只要求切应力为零，因此效率有所提高，在物理意义上也是合理的。

2.3 横向各向同性介质替换法

横向各向同性介质替换法[26](MS)的基本思想是利用横向各向同性介质近似代替自由表面，不直接对式(3)的所有应力条件进行处理，而仅令正应力σzz在自由表面处直接为零，切应力σxz为零的条件通过对自由表面上物性参数的设定，在波动方程交错网格有限差分迭代求解过程中实现。二维情况下MS的处理方式为

(7)

式中：σzz、ρx和λ、μ对应表示自由表面上的正应力、与vx相关的密度和拉梅常数；ρ1和μ1分别表示自由表面以下弹性介质的密度和剪切模量。图3展示各分量和参数在交错网格中分布情况。

图3 横向各向同性介质替换法自由表面取样位置

MS相对于镜像法而言，处理方式更简单，更易于编程实现，计算效率也更高。MS不需对虚拟层中的应力做镜像处理，只需在自由表面上对正应力σzz和部分弹性参数进行处理，就能满足式(3)自由表面边界条件的要求。

2.4 声学—弹性边界近似法

声学—弹性边界近似法(AEA)[27]考虑了自由表面上、下横向应力保持连续的条件，其他与MS思路大体相同。在二维情况下AEA的处理方式为

(8)

图4展示了自由表面在交错网格中的取位位置及各分量和参数在交错网格中的分布情况。

图4 声学—弹性边界近似法自由表面取样位置

不同于MS，AEA主要考虑自由表面上、下横向应力保持连续的条件，具体在式(8)中表现为2μ=2μ1，即拉梅常数μ不变。Xu等[27]指出MS违背了部分基本物理原理，而AEA较符合物理规律，且模拟精度更高。

3 均匀半空间模型数值模拟对比

本文选取标准交错网格高阶有限差分算法做瑞雷波波场数值模拟：采用时间2阶、空间12阶差分格式；力源为自由表面激发的z方向点力源，震源函数为主频20Hz、延迟时间50ms的高斯一阶导数；采集道数为60，最小炮检距为20m，道间距为1m；采用完美匹配层(Perfectly Matched Layer，PML)作为吸收边界条件，吸收宽度为20m，理论反射系数为0.000001(下同)。利用瑞雷波最小波长λmin与空间步长dh之比(points per minimum wavelength，ppw)度量网格剖分精度[15]，用Cagniard-De Hoop技术求解均匀半空间波场解析解[29]，以快速矢量传递算法正演理论频散曲线[30]，通过高分辨率线性拉东变换(Linear Radon Transform，LRT)提取频散能量图[31]。

本文首先设计均匀半空间模型(模型A)，其地质模型参数见表1。针对该模型分别从波场快照、波形曲线及频散曲线三个角度对自由表面边界条件进行定性—定量对比分析。

表1 均匀半空间模型A参数

3.1 波场快照对比

波场快照包含丰富波场信息，包括波的种类及其传播特性。通过波场快照，不仅可直观地再现瑞雷波在不同时刻的传播特性，而且可分析整个地震波场在不同时刻纵波、横波、转换波等与瑞雷波的相互关系、刻画各种波的能量分配方式，进而从地震波场传播角度评价四种自由表面边界条件用于瑞雷波波场数值模拟的可行性和优越性。设置模拟区域为100m×50m，时间步长dt=0.1ms，空间步长dh=0.25m，分别采用四种自由表面边界条件对模型A进行模拟，得到时间t=0.18s的波场快照。图5分别为SIM、MSIM、MS及AEA对应的vz和vx分量的波场快照。

由图5可知：瑞雷波(RW)在自由表面生成且沿自由表面传播，是一种面波；横波(S)以震源为中心向外传播，且充满整个空间，是一种体波；纵波速度远高于横波速度，在该时刻纵波已被PML完全吸收；瑞雷波速度稍慢于横波，但其能量在整个波场中占据主导地位。通过对比可知，四种方法均能生成符合勘探地球物理规律的波场快照，均适合作为瑞雷波波场数值模拟的自由表面边界条件。

3.2 不同网格剖分精度波形曲线对比

瑞雷波的模拟精度与网格剖分精度密切相关，为对比不同网格剖分精度下四种自由表面边界条件的数值模拟效果，设计了瑞雷波最小波长对应网格点数为10、20和40ppw的三组网格剖分参数(表2)。通过对模型A做模拟，得到对应炮集记录。图6是以AEA和20ppw网格剖分精度为例，模拟得到的均匀半空间vz和vx分量炮集记录。分别抽取炮集记录上炮检距为49m(第30道)处的单道地震记录，并与解析解进行对比，如图7所示。

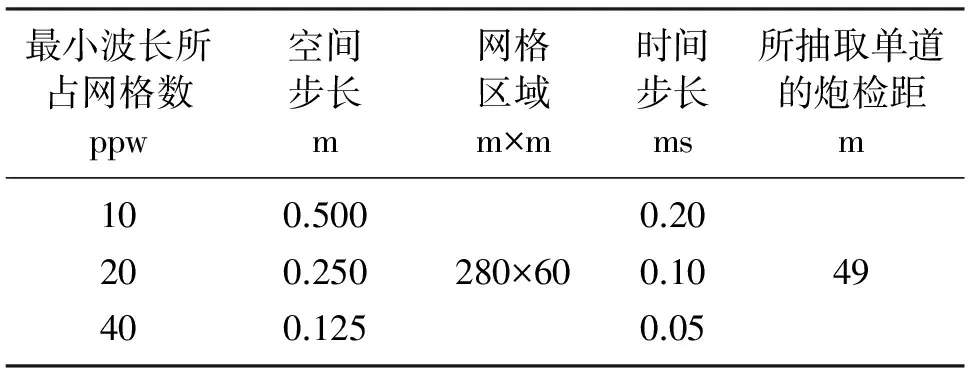
表2 均匀半空间模型网格剖分参数

从图6可知，因采用标准交错网格高阶有限差分数值模拟技术和PML吸收边界条件，大大削弱了数值频散和人工边界反射等数值模拟假象。炮集记录上既有能量占主导地位的瑞雷波，也有能量较弱的体波：瑞雷波清晰可见，同相轴为一条倾斜直线，在所有地震道上均具有很强能量；但体波仅在近道上可见明显波形，且其能量随着炮检距的增大而迅速减小。

为准确表征有限差分数值解与解析解的相对误差，应用L2范数误差量化不同情况下的模拟误差[15]

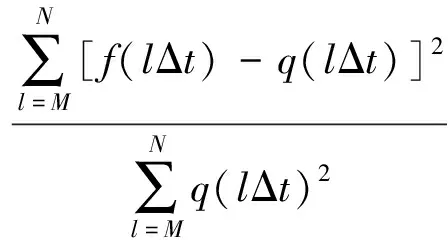
(9)

式中：f(lΔt)代表数值解；q(lΔt)代表解析解；MΔt和NΔt分别为瑞雷波的起跳时间和结束时间。显然，E越小，数值模拟精度则越高。利用式(9)可计算图7中瑞雷波波形曲线数值解与解析解的L2范数误差，计算结果见图8的误差变化曲线所示。

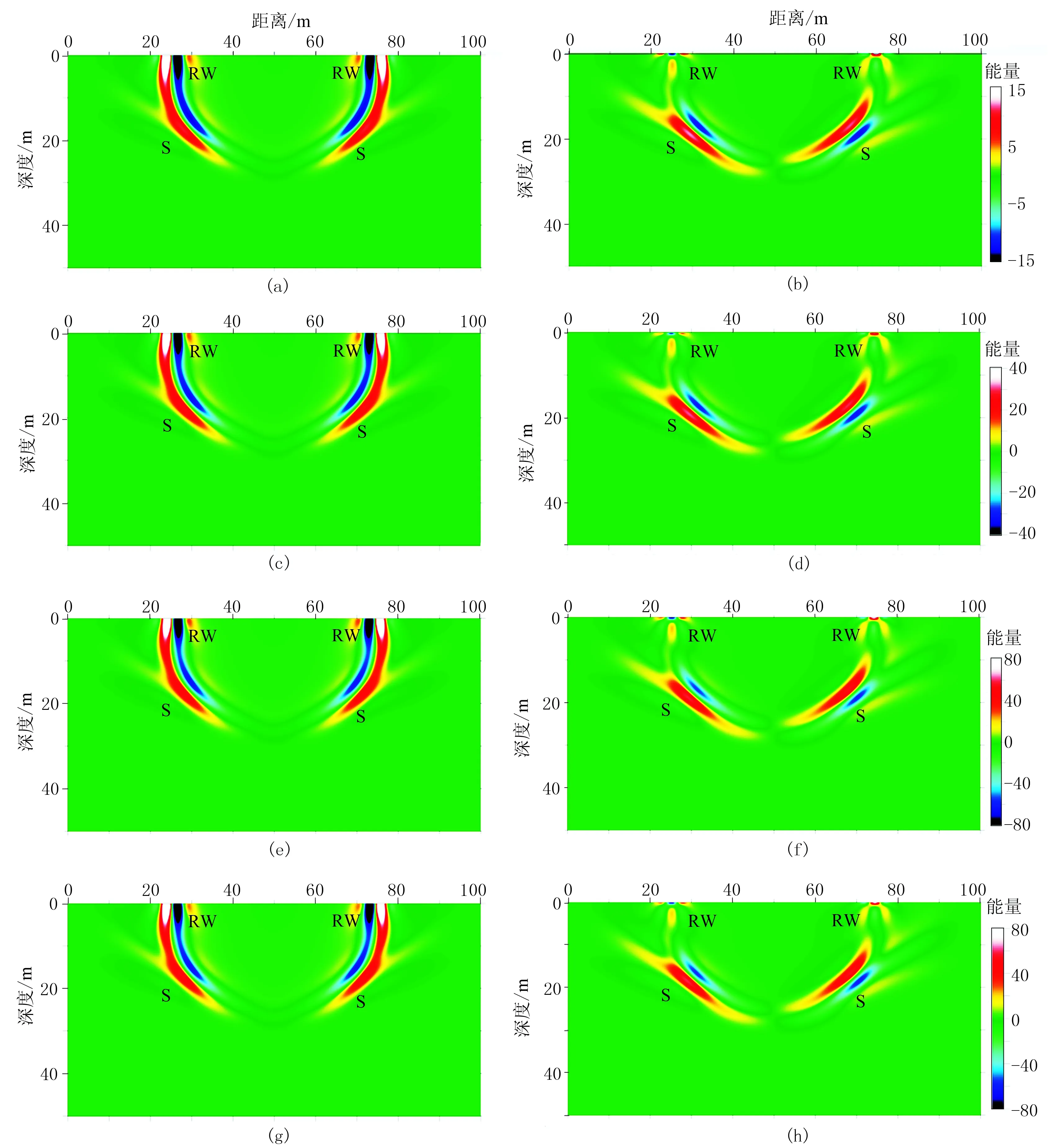
图5 均匀半空间模型t=0.18s时刻质点速度场快照

图6 均匀半空间模型的炮集记录

(a)AEA，vz分量； (b)AEA，vx分量

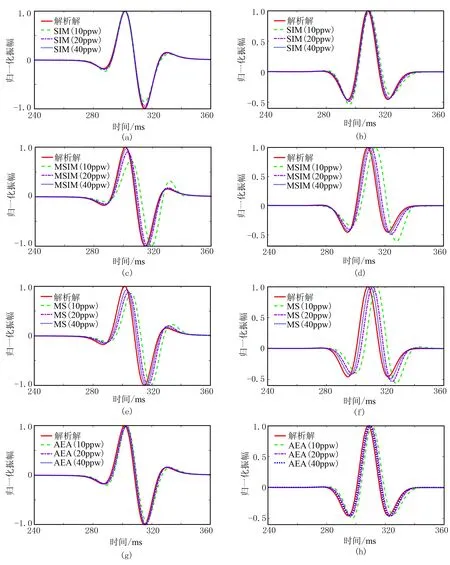
图7 四种自由边界条件在三种网格剖分精度下瑞雷波波形曲线数值解与解析解的对比

由图7可看出： SIM的波形拟合效果最好，其不同网格剖分精度对应的数值解与解析解都基本重合(图7a和图7b)； AEA的模拟精度仅次于SIM，其瑞雷波只存在轻微相移(图7g和图7h)； MSIM(图7c和图7d)和MS(图7e和图7f)的数值解不仅具有明显相移，也伴随明显的振幅改变，且网格剖分精度越低，该现象越明显。由图8可知，四种方法对应的L2范数相对误差都随网格剖分精度的提高而减小，SIM和AEA的相对误差变化较平缓，MSIM和MS的相对误差变化较大，说明SIM和AEA的稳定性更好。在粗网格剖分(10ppw)时，MS和MSIM的拟合相对误差极大，MS对应的vz和vx分量的相对误差分别高达63.90%和110.41%，MSIM对应的相对误差分别高达48.45%和83.42%，而AEA和SIM的拟合相对误差却较小，AEA对应的相对误差分别为9.94%和33.45%，SIM对应的相对误差最低，分别为1.28%和9.85%；在20ppw网格剖分情况下，MSIM和MS的拟合相对误差虽有明显减小，但与SIM和AEA的模拟精度仍有差距；当网格剖分精度为40ppw时，四种方法的误差较接近，但相对误差由低到高的顺序(SIM↗AEA↗MSIM↗MS)保持不变(图8)。通过定性—定量分析都可看出，在三种网格剖分精度下，SIM和AEA的数值模拟精度和稳定性都明显高于MSIM和MS，即使当网格剖分精度很低时，SIM和AEA仍能保持较高的模拟精度，而MSIM和MS却不能。

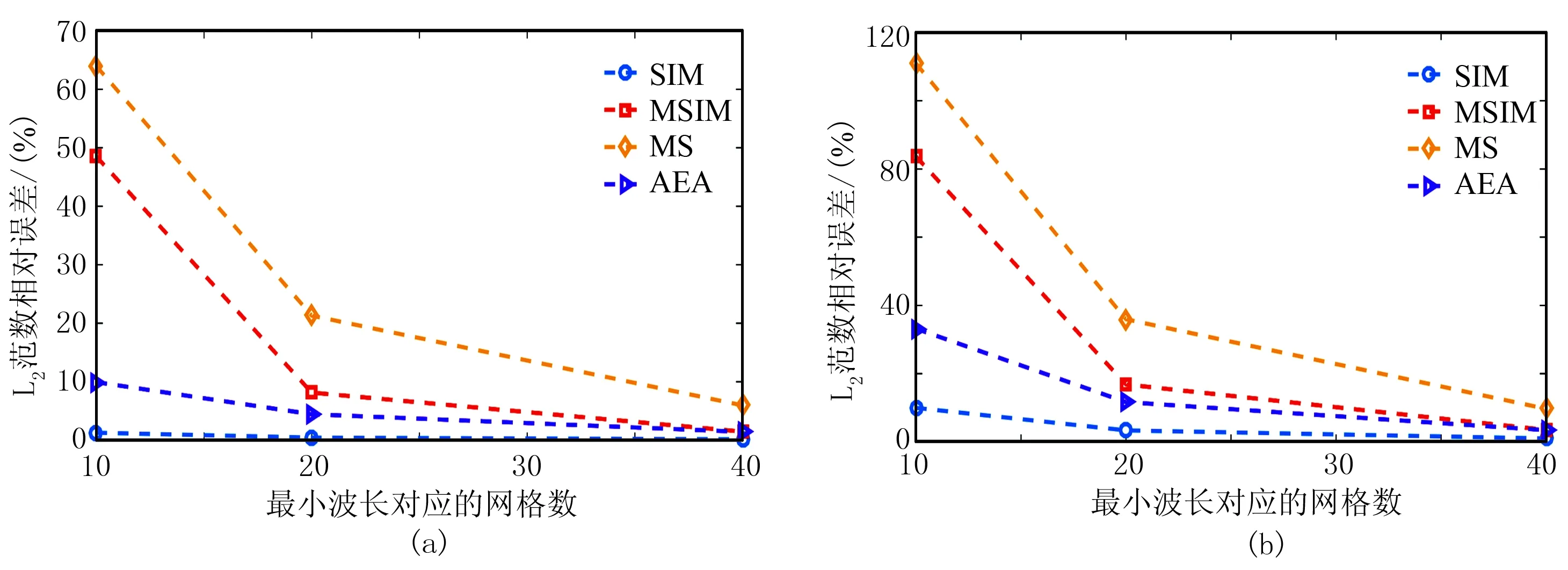
图8 四种自由边界条件对应的L2范数相对误差随网格剖分精度的变化情况

3.4 不同网格剖分精度频散曲线对比

瑞雷波不仅具有波形曲线解析解，还存在频散曲线解析解。波形曲线对比只利用了单道地震记录信息，所选择的目标地震道可能受瑞雷波近场效应和远场效应的影响，因此仅从该角度进行不同自由表面边界条件对比研究，得出的结论可能会有片面性。而频散曲线是瑞雷波最重要的特性，频散曲线综合考虑了多道地震记录信息，消除了瑞雷波近场效应和远场效应的影响，故有必要从频散曲线角度进行对比。二维瑞雷波数值模拟可采集到vz和vx分量的炮集记录，两个分量都包含模型信息，充分利用两个分量的信息，能更好地反映模型的真实情况。vz和vx炮集记录通过高分辨率LRT可分别得到vz和vx分量频散能量数据，再通过加权平均得到二分量频散能量数据。本文均采用该类型数据进行对比研究，权值均取为0.5。这样综合考虑了自由表面边界条件对两个分量模拟效果的影响。

为此，分别对图7中对应的炮集记录进行高分辨率LRT计算，得到相应的频散能量数据。图9a、图9c、图9e和图9g是以20ppw网格剖分精度，分别采用SIM、MSIM、MS、AEA得到的频散能量图。频散能量图上能量极大值点组成的曲线即为瑞雷波频散曲线数值解，分别从此四频散能量图中提取频散曲线数值解，并与解析解进行对比，得到图9b、图9d、图9f和图9h，而数值解与解析解的L2范数相对误差被绘制成误差变化曲线(图10)。

瑞雷波在均匀半空间不发生频散，其相速度为一定值，频散曲线解析解为一条水平直线。模拟得到的数值解只是近似解，并不能与解析解完全一致，其拟合误差会随着模拟精度的提高而减小。由图9a、图9c、图9e和图9g可直观看出：在同一网格剖分精度(20ppw)下，AEA模拟效果最好，解析解恰好从其频散能量极值区域中心处穿过(图9g)；其次是SIM，它对应的频散能量在高频处更收敛，但有轻微上扬(图9a)；而MSIM和MS在高频段存在不同程度的下跌(图9c和图9e)。

由图9b、图9d、图9f和图9h可知：三种网格剖分精度下，AEA对应的频散曲线数值解与解析解偏差都很小(图9h)；在粗网格剖分(10ppw)时，SIM(图9b)、MSIM(图9d)及MS(图9f)对应的数值解与解析解都存在不同程度的较大偏差，对应相对误差分别为8.1684E-05、3.3763E-04和1.5812E-04，而AEA的误差却仅有2.2193E-05(图10)。由图10可看出：随着网格剖分精度的提高，四种方法对应的误差都在减小； AEA的误差变化近似一条水平直线，SIM只是在10ppw时误差比AEA高，在20ppw和40ppw时，SIM和AEA数值模拟精度相当；从整体上看，MSIM和MS的误差都高于SIM和AEA；在40ppw时，四种方法的误差均很小，但SIM (1.5246E-05)和AEA(1.9670E-05)的数值模拟精度仍高于MSIM(2.3724E-05)和MS(2.9539E-05)。通过定性—定量分析易知，在三种网格剖分精度下，SIM和AEA的模拟精度和稳定性都明显高于MSIM和MS，即使在粗网格剖分(10ppw)时，SIM和AEA仍能保持较高的模拟精度，而MSIM和MS却不尽人意。

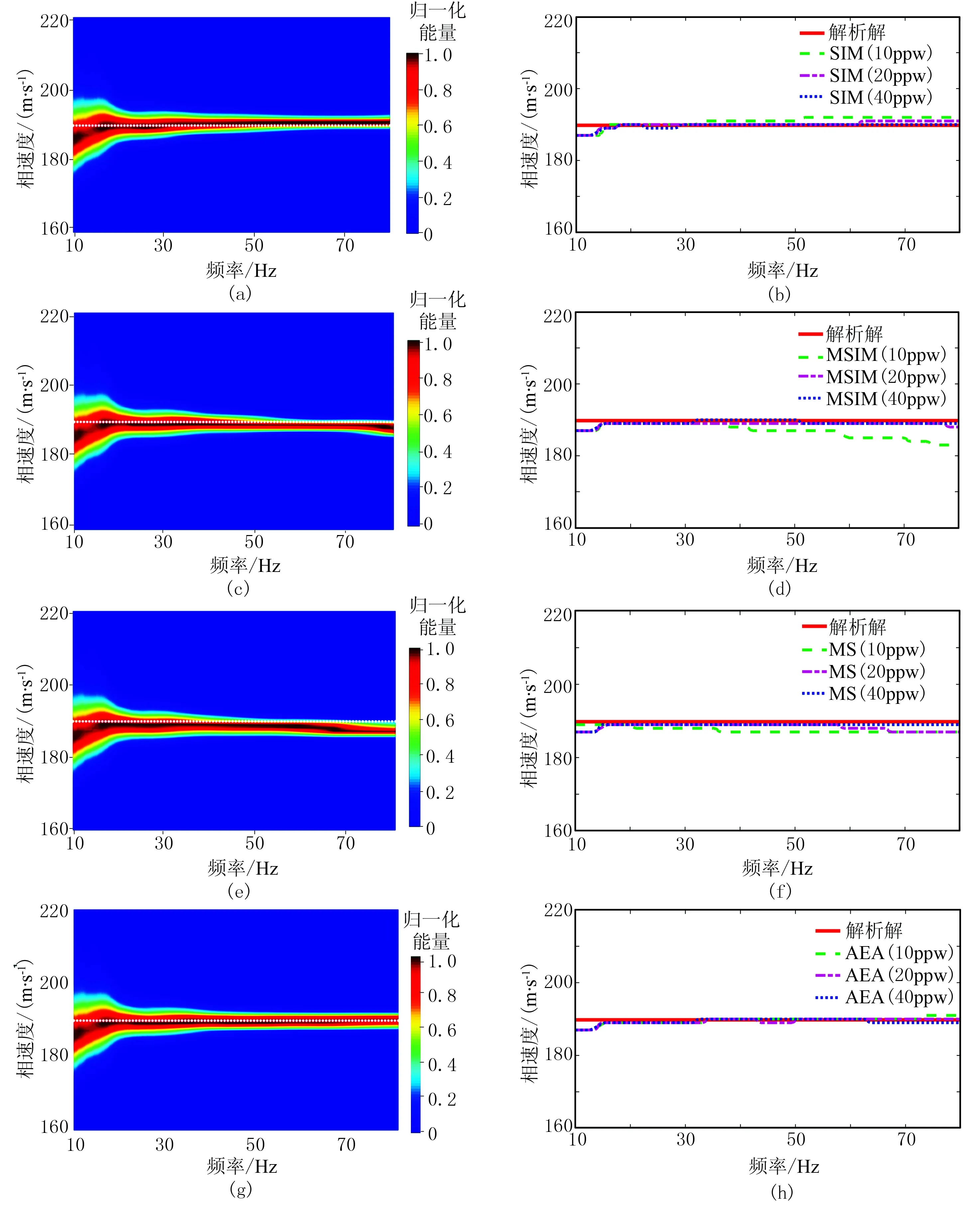
图9 四种自由边界条件对应的频散能量图和频散曲线数值解与解析解的对比图

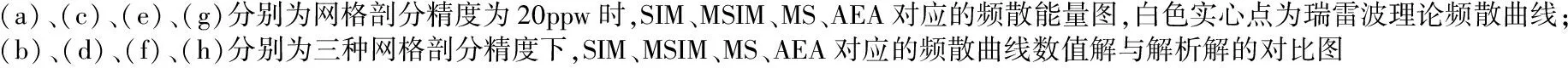
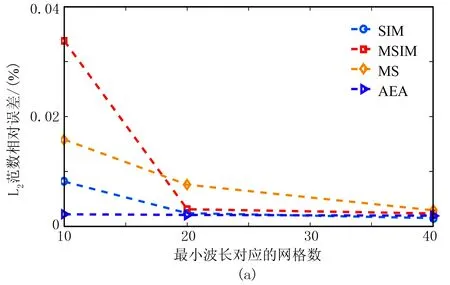
图10 四种自由边界条件对应的L2范数相对误差随网格剖分精度的变化

4 层状介质模型数值模拟对比

通过均匀半空间模型中定性—定量对比可知，在瑞雷波波场数值模拟中，SIM和AEA的模拟精度和稳定性都明显高于MSIM和MS。为验证该结论，并进一步对比SIM与AEA的优劣，又设计了三种典型的层状介质模型对四种自由表面边界条件的模拟效果进行对比。

4.1 两层速度递增模型

设计两层速度递增模型(模型B)，其地质模型参数如表3所示。设置时间步长dt=0.05ms，空间步长dh=0.25m，采集时长为0.9s，分别采用四种自由表面边界条件进行数值模拟，可得到对应的炮集记录。图11是以AEA为例，模拟得到的vz和vx分量炮集记录。炮集记录通过高分辨率LRT可得到对应的频散能量图(图12)。

由图11可看出，因采用标准交错网格高阶有限差分数值模拟技术和PML吸收边界条件，大大削弱了数值频散和人工边界反射等数值模拟假象。图中瑞雷波清晰可见，且呈发散的扫帚状。此外，还有直达波、折射波、反射波等体波，但瑞雷波具有更高的信噪比，其能量在整个地震记录中占主导地位。在图12频散能量图上，既有能量占主导地位的基阶模式，也有多条高阶模式发育，高阶模式随着阶数的增加，能量逐渐减弱；对于数值解与解析解的拟合程度，基阶模式拟合得最好，高阶模式随着阶数的增加，拟合度逐渐减小。四种自由表面边界条件的模拟结果中，AEA(图12d)的模拟效果最好，高阶模式的能量更为连续，且拟合度都较其他三种方法高，其次是SIM(图12a)和MS(图12c)，MSIM(图12b)的拟合情况相对最差。该模拟是在20ppw网格剖分精度情况下进行的，如果进一步提高网格剖分精度，四种方法的模拟效果会更好。

表3 两层速度递增模型B的参数

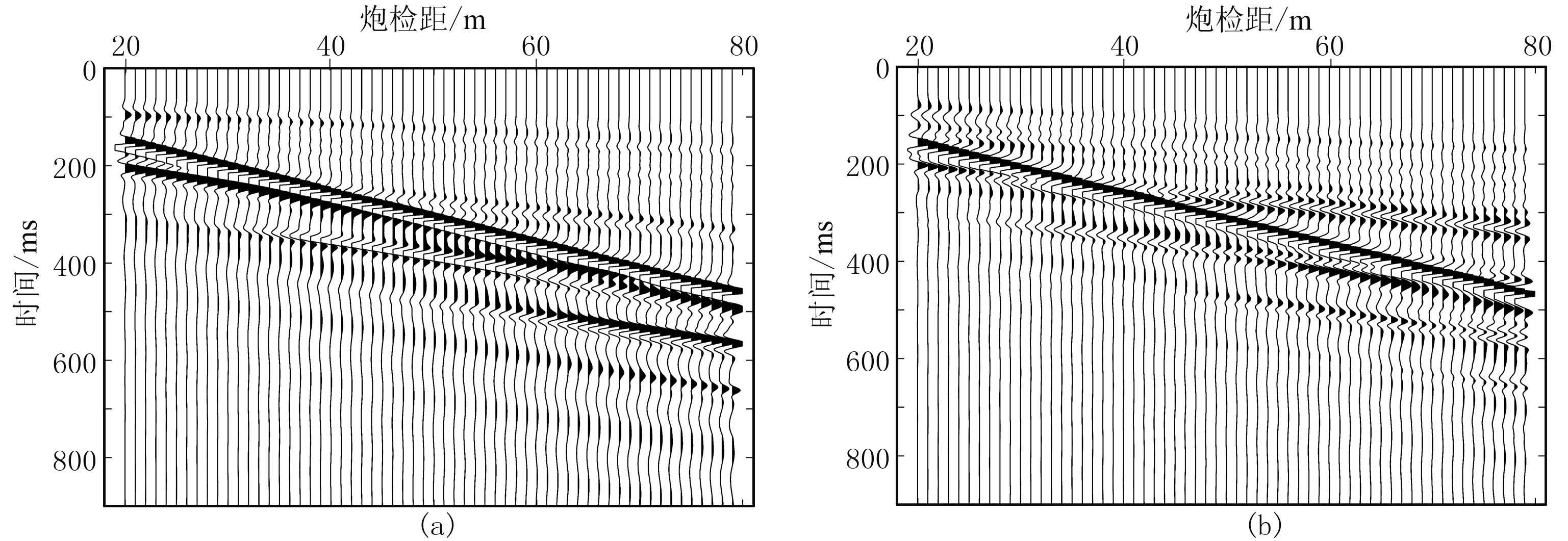
图11 两层速度递增模型的炮集记录

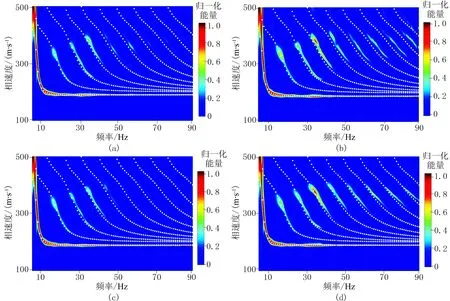
图12 四种自由表面边界条件对应的两层速度递增模型的频散能量图

4.2 三层含低速软夹层模型

设计三层含低速软夹层模型(模型C)，其地质模型参数如表4所示。设置时间步长dt=0.05ms，空间步长dh=0.25m，采集时长为0.9s，通过数值模拟可得到对应的炮集记录。图13是以AEA为例模拟得到的vz和vx分量炮集记录。炮集记录通过高分辨率LRT可得到对应的频散能量图(图14)。

在图14频散能量图上既有基阶模式，也有高阶模式，基阶模式与高阶模式能量都很强，且均有截止频率，如基阶模式截止频率约为20Hz，第一高阶模式截止频率约为28Hz。由于低速夹层的存在，高阶模式存在严重的“模式接吻”现象[32](图14a红圈圈出部分)。在5～20Hz频段内，四种方法对应的基阶模式与解析解均拟合得很好；在20～40Hz频段内，四种方法对应的第一和第二高阶模式与解析解都存在一定程度的偏差；在40～90Hz频段内，AEA的数值解与解析解拟合情况最好，解析解正好从频散能量图极大值区域的中心穿过，其次是SIM，但是其能量图分辨率和连续性较差，MSIM和MS的拟合情况相当，均与解析解有一定程度的偏差。

表4 三层含低速软夹层模型C的参数

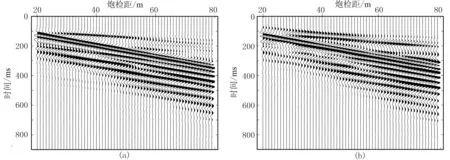
图13 三层含低速软夹层模型的炮集记录

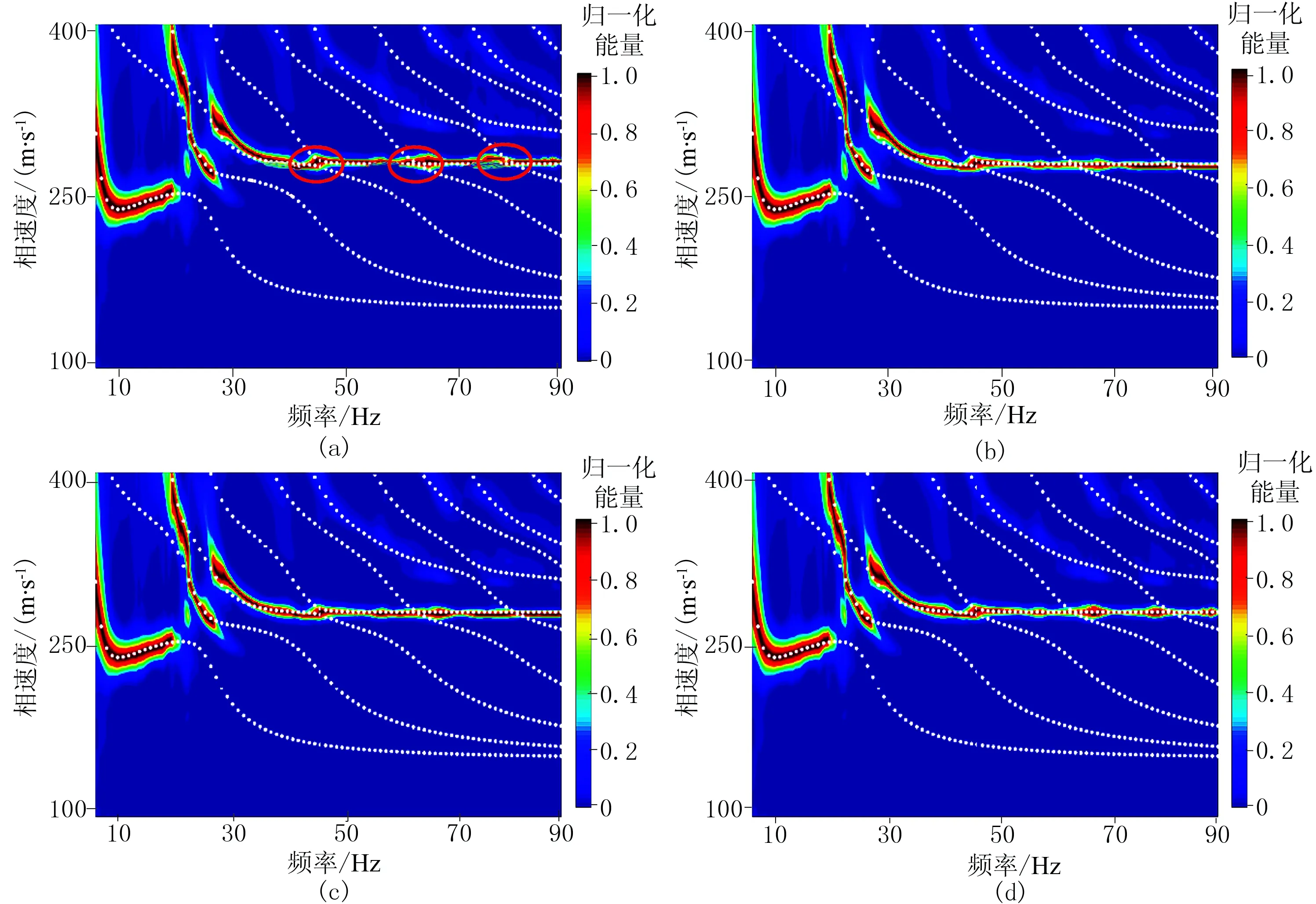
图14 四种自由表面边界条件对应的三层含低速软夹层模型的频散能量图

4.3 四层含高速硬夹层模型

设计四层含高速硬夹层模型(模型D)，其地质模型参数如表5所示。设置时间步长dt=0.04ms，空间步长dh=0.125m，采集时长为0.8s，经数值模拟可得到对应的炮集记录。图15是以AEA为例模拟得到的vz和vx分量炮集记录。炮集记录通过高分辨率LRT可得到对应的频散能量图(图16)。

该模型既是高泊松比又含高速硬夹层，数值模拟难度有所增加，故采用40ppw网格剖分精度进行模拟。由图16可知，四种方法对应的频散能量图上，基阶模式在所有频段内能量都很强，第一高阶模式仅在10～20Hz频段内能量较强，其他高阶模式能量都很弱，甚至未发育。在该精度条件下，四种方法对应的数值模拟效果相当，仅在10～30Hz频段内可发现较小差异，即此频段内AEA的模拟精度最高，其基阶和第一高阶的频散能量最大值比另三种方法都更接近于解析解(图16d)。

表5 四层含高速硬夹层模型D的参数

图15 四层含高速硬夹层模型的炮集记录

图16 四种自由表面边界条件对应的四层含高速硬夹层模型的频散能量图

5 结论

本文基于标准交错网格高阶有限差分算法，分别在均匀半空间、两层速度递增、三层含低速软夹层和四层含高速硬夹层模型中，对瑞雷波波场数值模拟中最具代表性的四种自由表面边界条件：应力镜像法(SIM)、改进应力镜像法(MSIM)、横向各向同性介质替换法(MS)、声学—弹性边界近似法(AEA)，进行了数值模拟对比研究。结果表明：

(1)在均匀半空间模型中，四种方法均能生成符合勘探地球物理规律的波场快照；四种方法对应的瑞雷波波形曲线和频散曲线的数值解与解析解的拟合误差都随网格剖分精度的提高而减小。在相同网格剖分情况下，SIM和AEA的模拟精度和稳定性都明显高于MSIM和MS。即使在粗网格剖分时，SIM和AEA仍有很高模拟精度，而MSIM和MS对应的相对误差却较大。

(2)层状介质模型的模拟结果，验证了均匀半空间模型中的结论，并进一步对比了SIM和AEA的模拟精度。结果表明，在复杂层状介质模型中，AEA的模拟精度一定程度上优于SIM。

综上所述，在瑞雷波有限差分数值模拟中，对于简单模型，SIM和AEA都能得到比MSIM和MS更高精度的模拟结果；对于复杂地质模型，AEA的模拟效果最好、精度最高，是最适合瑞雷波数值模拟的自由表面边界条件。

本文是在各向同性弹性介质条件下展开研究，虽然所设计模型考虑了实际浅地表高泊松比的特点，但实际浅地表环境更复杂，既具有各向异性，又具有黏弹性。那么，对于各向异性黏弹性介质瑞雷波数值模拟，其自由表面边界条件该如何设置？这有待后续深入研究、探讨。

感谢中国地质大学(武汉)地球物理与空间信息学院汪利民老师分享计算弹性均匀半空间波场解析解的程序。

[1] Xia J H，Miller R D，Park C B.Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves.Geophysics，1999，64(3)：691-700.

[2] Park C B，Miller R D，Xia J H.Multichannel analysis of surface waves (MASW).Geophysics，1999，64(3)：800-808.

[3] 董良国，马在田，曹景忠.一阶弹性波方程交错网格高阶差分解法稳定性研究.地球物理学报，2000，43(6)：856-864.

Dong Liangguo，Ma Zaitian，Cao Jingzhong.A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation.Chinese Journal of Geophysics，2000，43(6)：856-864.

[4] 周竹生，刘喜亮，熊孝雨.弹性介质中瑞雷面波有限差分法正演模拟.地球物理学报，2007，50(2)：567-573.

Zhou Zhusheng，Liu Xiliang，Xiong Xiaoyu.Finite difference modelling of Rayleigh surface wave in elastic media.Chinese Journal of Geophysics，2007，50(2)：567-573.

[5] 熊章强，张大洲，秦臻等.瑞雷波数值模拟中的边界条件及模拟实例分析.中南大学学报(自然科学版)，2008，39(4)：824-830.

Xiong Zhangqiang，Zhang Dazhou，Qin Zheng et al.Boundary conditions and case analysis of numerical modeling of Rayleigh wave.Journal of Central South University (Science and Technology Edition)，2008，39(4)：824-830.

[6] 邵广周，李庆春，吴华.基于波场数值模拟的瑞利波频散曲线特征及各模式能量分布.石油地球物理勘探，2015，50(2)：306-315.

Shao Guangzhou，Li Qingchun，Wu Hua.Dispersion curves and mode energy distribution of Rayleigh wave based on wavefield numerical simulation.OGP，2015，50(2)：306-315.

[7] 李振春，张慧，张华.一阶弹性波方程的变网格高阶有限差分数值模拟.石油地球物理勘探，2008，43(6)：711-716.

Li Zhenchun，Zhang Hui，Zhang Hua.Variable-grid high-order finite-difference numeric simulation of first-order elastic wave equation.OGP，2008，43(6)：711-716.

[8] 杜启振，白清云，李宾.横向各向同性介质优化差分系数法地震波场数值模拟.石油地球物理勘探，2010，45(2)：170-176.

Du Qizhen，Bai Qingyun，Li Bin.Optimized difference coefficient method seismic wave field numerical simulation in vertical transverse isotropic medium.OGP，2010，45(2)：170-176.

[9] Wang L M，Luo Y H，Xu Y X.Numerical investigation of Rayleigh-wave propagation on topography surface.Journal of Applied Geophysics，2012，86(11)：88-97.

[10] 高静怀，何洋洋，马逸尘.黏弹性与弹性介质中Rayleigh面波特性对比研究.地球物理学报，2012，55(1)：207-218.

Gao Jinghuai，He Yangyang，Ma Yichen.Comparison of the Rayleigh wave in elastic and viscoelastic media.Chinese Journal of Geophysics，2012，55(1)：207-218.

[11] 杨宇，黄建平，雷建设等.Lebedev网格黏弹性介质起伏地表正演模拟.石油地球物理勘探，2016，51(4)：698-706.

Yang Yu，Huang Jianping，Lei Jianshe et al.Numerical simulation of Lebedev grid for viscoelastic media with irregular free-surface.OGP，2016，51(4)：698-706.

[12] 张煜，徐义贤，夏江海等.含流体孔隙介质中面波的传播特性及应用.地球物理学报，2015，58(8)：2759-2778.

Zhang Yu，Xu Yixian，Xia Jianghai et al.Characteristics and application of surface wave propagation in fluid-filled porous media.Chinese Journal of Geophy-sics，2015，58(8)：2759-2778.

[13] Yuan S Y，Wang S X，Sun W J et al.Perfectly matched layer on curvilinear grid for the second-order seismic acoustic wave equation.Exploration Geophysics，2014，45(2)：94-104.

[14] 裴正林.任意起伏地表弹性波方程交错网格高阶有限差分法数值模拟.石油地球物理勘探，2004，39(6)：629-634.

Pei Zhenglin.Staggered-grid high-order finite-difference numerical simulation of elastic wave equation for any irregular surface.OGP，2004，39(6)：629-634.

[15] Bohlen T，Saenger E H.Accuracy of heterogeneous staggered-grid finite-difference modeling of Rayleigh waves.Geophysics，2006，71(4)：T109-T115.

[16] Aki K，Richards P G.Quantitative Seismology：Theory and Methods.W H Freeman，New York，1980.

[17] Levander A R.Fourth-order finite-difference P-SV seismograms.Geophysics，1988，53(11)：1425-1436.

[18] Robertsson J O A.A numerical free-surface condition for elastic/viscoelastic finite-difference modeling in the presence of topography.Geophysics，1996，61(6)：1921-1934.

[19] Crase E.High-order (space and time) finite-difference modeling of the elastic wave equation.SEG Technical Program Expanded Abstracts，1990，9：987-991.

[20] Hestholm S，Ruud B O.3-D finite-difference elastic wave modeling including surface topography.Geophysical Prospecting，1994，42(5)：371-390.

[21] Kosloff D，Kessler D，Filho A Q et al.Solution of the equations of dynamic elasticity by a Chebychev spectral method.Geophysics，1990，55(6)：734-748.

[22] 王秀明，张海澜.用于具有不规则起伏自由表面的介质中弹性波模拟的有限差分算法.中国科学G辑，2004，34(5)：481-493.

Wang Xiuming，Zhang Hailan.Modeling the seismic wave in the media with irregular free interface by the finite-difference method.Science in China (Series G)，2004，34(5)：481-493.

[23] Boore D.Finite difference methods for seismic wave propagation in heterogeneous materials∥Methods in Computational Physics：Advances in Research and Applications，Academic Press,London,1972，11：1-37.

[24] Zahradnik J，Priolo E.Heterogeneous formulations of elastodynamic equations and finite-difference schemes.Geophysical Journal International，1995，120(3)：663-676.

[25] Graves R W.Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences.Bulletin of Seismological Society of America，1996，86(4)：1091-1106.

[26] Mittet R.Free-surface boundary conditions for elastic staggered-grid modeling schemes.Geophysics，2002，67(5)：1616-1623.

[27] Xu Y，Xia J，Miller R D.Numerical investigation of implementation of air-earth boundary by acoustic-elastic boundary approach.Geophysics，2007，72(5)：SM147-SM153.

[28] 王周，李朝晖，龙桂华等.求解弹性波有限差分法中自由边界处理方法的对比.工程力学，2012，29(4)：77-83.

Wang Zhou，Li Chaohui，Long Guihua et al.Comparison among implementations of free-surface boundary in elastic wave simulation using the finite-difference method.Engineering Mechanics，2012，29(4)：77-83.

[29] Berg P，If F，Nielsen P et al.Analytical reference solutions,Advanced seismic modeling//Modeling the Earth for Oil Exploration (Helbig K Ed).Pergamon Press，New York,1994，421-427.

[30] 凡友华，刘家琦，肖柏勋.计算瑞利波频散曲线的快速矢量传递算法.湖南大学学报(自然科学版)，2002，29(5)：25-30.

Fan Youhua，Liu Jiaqi，Xiao Boxun.Fast vector-transfer algorithm for computation of Rayleigh wave dispersion curves.Journal of Hunan University (Natural Sciences Edition)，2002，29(5)：25-30.

[31] Luo Y H，Xia J H，Miller R D et al.Rayleigh-wave dispersive energy imaging using a high-resolution linear Radon transform.Pure and Applied Geophysics，2008，165(5)：903-922.

[32] 夏江海，高玲利，潘雨迪等.高频面波方法的若干新进展.地球物理学报，2015，58(8)：2591-2605.

Xia Jianghai，Gao Lingli，Pan Yudi et al.New findings in high-frequency surface wave method.Chinese Journal of Geophysics，2015，58(8)：2591-2605.

*湖北省武汉市洪山区鲁磨路388号中国地质大学地球物理与空间信息学院，430074。 Email：xhsong@cug.edu.cn

本文于2017年1月2日收到，最终修改稿于2017年10月4日收到。

本项研究受国家自然科学基金项目(41574114、41174113)和中国地质大学(武汉)教学实验室开放基金项目(SKJ2016098)联合资助。

1000-7210(2017)06-1156-14

袁士川，宋先海，蔡伟，胡莹，鲁鹏.瑞雷波有限差分数值模拟中不同自由表面边界条件的对比.石油地球物理勘探，2017,52(6):1156-1169.

P631

10.13810/j.cnki.issn.1000-7210.2017.06.005

(本文编辑：朱汉东)