基于选权迭代的走航式水声差分定位方法

2017-12-18王振杰吴绍玉刘慧敏

石油地球物理勘探 2017年6期

赵爽王振杰吴绍玉王毅刘慧敏单瑞

(①中国石油大学(华东)地球科学与技术学院，山东青岛 266580； ②海洋国家实验室海洋矿产资源评价与探测技术功能实验室，山东青岛 266071； ③东方地球物理公司，河北涿州 072751； ④海洋石油工程股份有限公司，山东青岛 266520； ⑤中国地质调查局青岛海洋地质研究所，山东青岛 266071)

·采集技术·

基于选权迭代的走航式水声差分定位方法

赵爽*①王振杰①②吴绍玉③王毅④刘慧敏①单瑞⑤

水下声学定位中存在应答器时延等系统误差，若采用传统的几何法定位，因系统误差难以改正或消除而导致定位精度降低。针对该问题，本文采用历元间差分的方式减弱或消除系统误差。结合石油物探走航式水下定位实际，给出了相应的水下差分模型。同时，考虑到水下声学观测值中不可避免地存在粗差，采用基于选权迭代的抗差估计进行解算。模拟算例和实测数据验证结果表明：历元间差分定位方法定位精度优于传统的几何法，国产BPS水下声学定位系统在50m以内水深可实现1m定位精度。

水下声学定位差分算法走航式选权迭代抗差估计

1 引言

随着海洋战略的推进，海洋勘探与开发活动广泛开展，需要获取大范围、准确的海洋空间与环境数据，高精度的水下定位技术是重要基础和保障。由于水声观测的动态性、仪器自噪声、外部环境以及其他诸多因素的影响，致使水下声学观测值不可避免地存在一定的系统误差和粗差，如果不予减小或消除，将会影响定位结果及其应用[1,2]。

国内外专家学者在水下定位模型改进和抗差估计方面进行了大量的研究。在水下定位模型方面，传统的几何法定位模型简单，但在抵抗系统误差影响方面呈现弱势。Xu等[3]首先提出水下差分定位方法；Zhao等[4]视时间延迟误差为解算参数，构建水下定位模型； Yang等[5]提出了一种无需测量声速剖面进行水下静态目标定位的方法；蔡艳辉等[6]基于GPS智能浮标，构建了几何法定位模型并做了精度分析；Yan等[7]顾及不确定声速并视其为解算参数，研究了浮标移动长基线定位算法。上述模型在水下定位方面得到了较广泛的应用。在抗差估计方面，周江文[8]从等价权出发提出有效的IGG估计方案；Yang等[9]提出了基于双因子等价权的相关观测值的抗差估计方法； Xu[10]提出了一种符号约束的抗差估计方法；王潜心等[11]采用粗差探测与抗差估计相结合的方法来处理GPS动态定位中的粗差问题；张志伟等[12]将抗差估计应用到多波束测深异常值探测中，抗差估计方法在GNSS(Global Navigation Satellite System,全球导航卫星系统)定位领域应用广泛且效果显著，但在水下定位方面应用还不多。

鉴于石油勘探、海洋调查等领域多采用基于测量船的走航模式[13]，本文针对走航式水下声学定位，推导了水下差分定位算法，并首次探讨将水下差分定位应用到海上石油勘探过程中。为减小部分水下定位系统误差和空间相关性误差影响，同时结合水下声学定位过程中常见的观测值包含粗差的问题，给出了基于选权迭代方法的抗差估计解算步骤，最后通过模拟算例和实测数据予以验证。

2 传统几何法水下定位原理

在水下定位中，安置在船底的换能器发射声信号，海底的应答器接收信号并反馈应答信号被换能器接收，以此来获取声信号传播时间；通过声速剖面仪测量声速，声速乘以单程传播时间可获得距离观测值。理论上当获得三个以上的距离观测值后，可交会出应答器的三维坐标。

假设海底应答器T坐标为(xT,yT,zT)，Pi为(i=1,2,…,n)历元换能器的位置，其坐标为(xi,yi,zi)，ti为Pi与T之间声波传播的往返时间，C为平均声速，那么

(1)

通常为了提高定位的可靠性，会测量多组观测值，然后基于最小二乘原理进行平差解算以求目标位置。

3 水下差分法定位原理

当进行水下定位时，由于水声观测的动态性、仪器自噪声、外部环境以及其他诸多因素的影响，系统受到来自水面以及水下的各类误差的影响，如测量船位置误差、声速误差和应答器时延误差等，限制了水下定位精度[14]。若使用GPS RTK为测量船定位，精度可以达到厘米级，远高于其他外围设备，因此该误差可以忽略不计。对于其他系统误差和粗差，传统的定位模型不能很好地加以消除。

结合水下定位实际，测量船在海面持续走航作业，假设相邻历元下测量船的位置在时间和空间上足够接近，可以认为两条声线经过的声速结构是相似的，考虑到对同一个海底应答器进行的不同声学观测中包含了相同的应答器时间延迟误差，那么观测值历元间做差，可以减小甚至消除应答器时延误差及与声速结构有关的系统误差，从而一定程度上提高定位精度[3]。

3.1 历元间单差定位函数模型

如图1所示，假设ti时刻由GPS给出的测量船位置为xi，海底应答器的坐标为xo，测得的测量船至应答器的距离(传播时间乘以声速)为ρsio，则有

ρsio=f(xo,xi)+δρdsio+δρv sio+εio

(2)

式中：f(xo,xi)为测量船到海底应答器的真实距离； δρdsio为与传播时间有关的系统误差； δρvsio为与声速有关的系统误差；εio为测距随机误差。将式(2)线性化后

δρv sio+εio+bsioεxs i

(3)

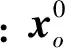
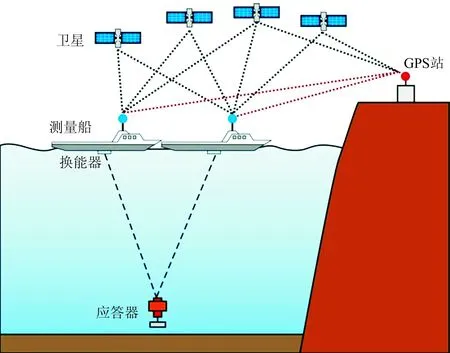
图1 走航式水下声学差分定位示意图

假设tj时刻线性化后的方程有

δρv sjo+εjo+bsjoεxs i

(4)

上式中各符号对应历元为tj时刻，物理意义与式(3)同理，不再赘述。

式(4)和式(3)作差，可得

Δρij=(asjo-asio)dxo+Δρdsijo+Δρv sijo+Δεijo

(5)

其中

式中： Δρij为常数项； Δρdsijo为差分后的时间延迟引起的误差项； Δρv sijo为差分后的声速相关误差项； Δεijo为偶然误差项。

在实际的水下定位中，常采用CTD(Conductivity-Temperature-Depth，盐温深)测量系统获取声速结构，声速随水介质的温度、盐度和压力的不同而不同，同时由于水介质本身的温、盐、压的时变特性也会带来声速的测量误差[15,16]。当水深较深时， CTD系统获得声速结构需要数小时，所以测量误差主要是受声速结构的日变化和海洋内波的影响。Yamada等[17]研究表明，季节变化虽然也对声速剖面有所影响，但其对水下点定位的影响要比声速剖面结构的日变化小得多。Spiess等[18]指出，把声速变化20min一个周期、声信号传播的等效距离大约为20cm这些现象和影响归结为海洋内波的原因。

结合水下定位实际，可认为式(5)中测量船的位置xi、xj是连续的、且在空间和时间上足够接近，两条声线经过的声速结构相似，那么两历元观测量中包含相似的声速空间相关性误差。如果声速的变化是由内波引起的短期变化，只要测量船在内波短周期之内到达下一个观测点(要求船速足够快)，那么仍然可以认为式(5)中δρv sio≈δρv sjo，即Δρv sijo≈0。否则，每个单差观测方程中引入了一个未知的偏差量Δρv sijo，必然影响定位精度。如果测量船采用对称航迹进行定位，则可以降低该误差的影响。由于ρsio、ρsjo为同一个换能器测量所得的到水下应答器的距离，所以由应答器引起的时间延迟造成的系统误差是相同的，通过历元间差分可以消除该误差的影响，因此Δρdsijo=0。

当j=i+1时，单差误差方程可以表示为

Δρi(i+1)=(asi+1o-asio)dxo+Δεi(i+1)o

(6)

如果由短期内波引起的声速结构变化误差可以忽略的话，那么观测方程可统一表示为

l=Adxo+εl

(7)

式中：l为常数项；A为观测方程系数矩阵；εl为观测过程中的偶然误差。其具体表达式为

(8)

令f(xo,xi)=fi，那么

(9)

(10)

误差方程可以写为

V=Adxo-l

(11)

式中V为残差向量。

3.2 历元间单差定位随机模型

法方程为

ATPAdxo-ATPl=0

(12)

式中P为观测值的权矩阵。下面是对权矩阵P的推导。

式(10)可写为

(13)

式中

需要说明的是，bsio和εxsi分别为1×3和3×1的矩阵。

换能器位置误差主要包括动态GPS定位误差和姿态误差，由于姿态误差相对比较小，可以用动态GPS的定位误差来代替换能器位置误差。

观测值误差协方差阵为

(14)

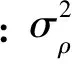
由式(13)根据协方差传播率

DD=CDCT

(15)

而

(16)

3.3 定位模型解算

在实际的水下声学定位中，由于水声观测的动态性、仪器自噪声、外部环境以及其他诸多因素的影响，水下声学观测值中常包含粗差，会降低水下声学定位精度。抗差估计是在粗差不可避免的情况下，选择估计方法使得未知参数的估值尽可能避免粗差的影响。基于选权迭代方法的抗差模型在抵抗粗差方面具有一定优势。选权迭代法从以下最小条件出发

(17)

IGG3权函数[19,20]

(18)

其中k0一般取1.0～1.5，k1一般取2.5～3.0，σ为方差因子。式(18)中权函数采用三段法[21]：对正常观测值采用保权处理(保权区)；对可疑观测值采用降权处理(降权区)；对异常观测值使权为0(拒绝区)，并予以淘汰。

基于选权迭代法的水下单差定位模型解算一般步骤如下。

(1)按照最小二乘法求解待估参数及其残差

(19)

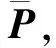
(20)

(3)最终可得应答器坐标位置及观测值改正数

(21)

(4)验后单位权中误差、平差参数协方差阵

(22)

选权迭代抗差估计通过引入等价权矩阵来调节各观测值对估值结果的贡献，提高了估值结果的准确性和可靠性[19]。

4 算例分析

4.1 仿真算例分析

模拟海上石油勘探OBC(Ocean Bottom Cable，海底电缆)声学二次定位[22,23]数据采集过程。模拟两条测线，测量船沿一定水平间距的测线航行。仿真实验分别模拟水下50m和100m处一组应答器阵列，相邻应答器间距为40m。假设船速为4节(1节=1.852km/h)，采样间隔为4s, 模拟水面波高为2m的余弦波动。声速剖面采用Munk理想声速剖面，表层声速为1548m/s，采用分层等梯度射线声学跟踪算法[16,24]仿真传播时间。

系统误差采用文献[3]中的公式

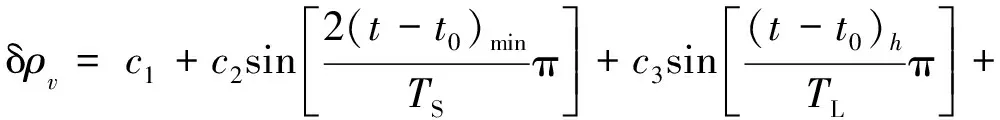
(23)

式中主要包括四部分的系统误差：c1为常数项系数；c2为短周期内波误差项系数；c3为长周期误差项系数；c4为测区影响因素系数。TS、TL分别为内波短周期和长周期，单位分别是min和h;t、t0分别为走航中数据采集时刻和初始测量时刻。根据文献[17]和文献[18]的分析及描述的内波长、短周期，各参数设置如下：c1=10，c2=12，c3=30，c4=2，单位为cm；TS=15，TL=12，scon=2000m,‖xo-xi‖为测量船换能器至海底应答器的斜距。偶然误差参考文献[3]，换能器定位中误差各方向为10cm，应答器时延误差为5cm[25]。

实验方案设计如表1所示。

表1 仿真实验设计方案

以水深为100m、测线间距为200m为例，声速剖面如图2所示，模拟测量船航迹和应答器位置示意图见图3。

对仿真实验中系统误差影响和差分后系统误差影响进行分析。图4为模拟的长、短周期系统误差差分前后效果对比图。

图2 Munk理想声速剖面

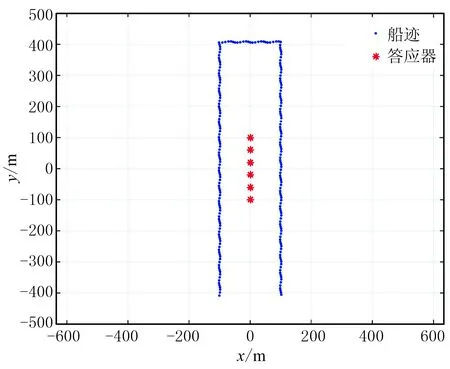
图3 船迹和应答器位置示意图

图4 模拟的系统误差及差分后效果

由图4可以看出，相邻历元间差分后的短周期内波的影响被大幅减弱，长周期误差项也基本被消除。因此当对历元相近的观测值之间进行差分，可以有效地削弱系统误差对定位结果的影响。

根据表1的方案，模拟实验200次，用传统几何定位算法和基于选权迭代抗差估计的历元差分定位算法分别进行解算，解算效果如图5、图6所示。

图5 几何法和差分法水下定位精度(水深为50m)

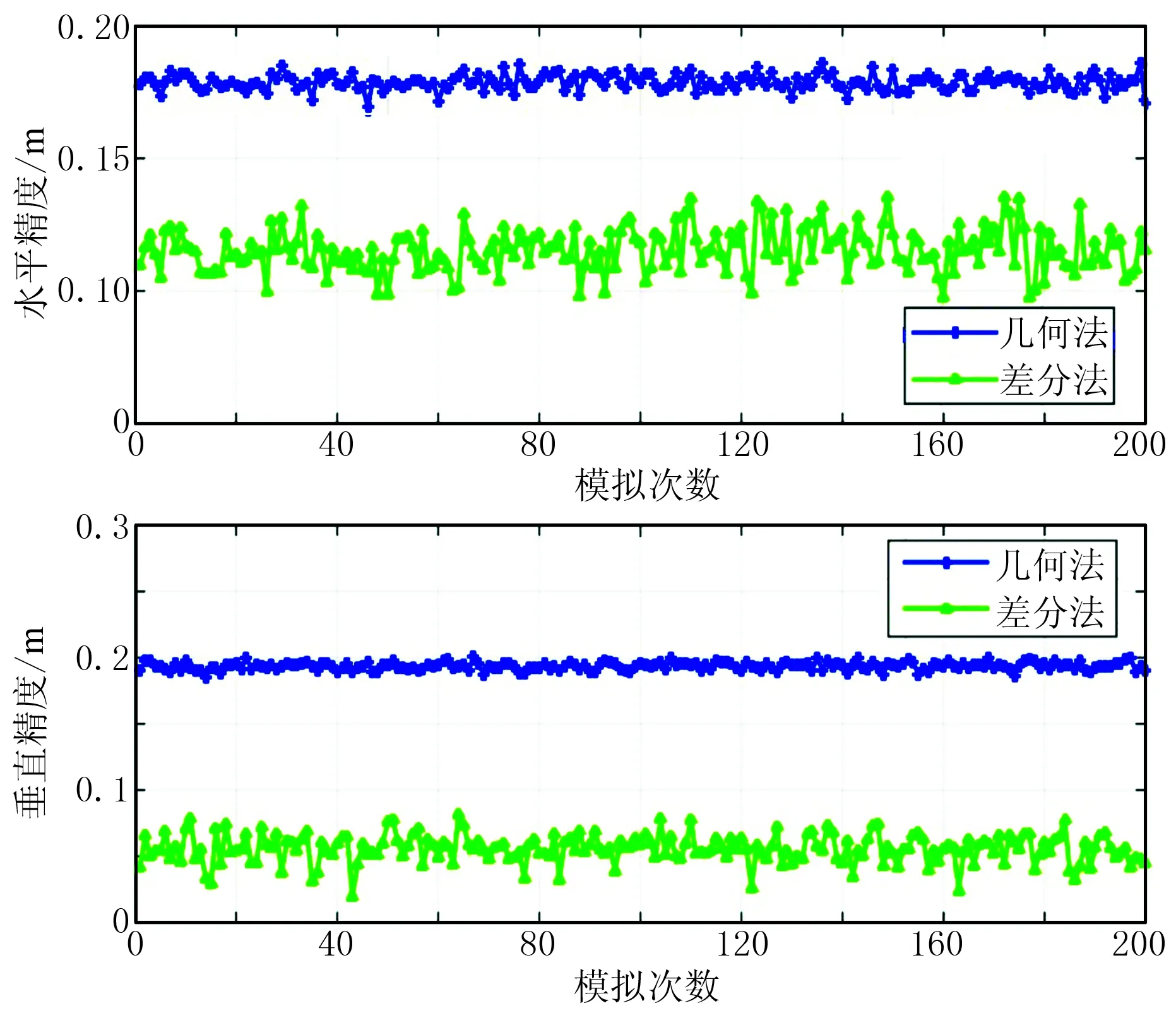
图6 几何法和差分法水下定位精度(水深为100m)

对随机模拟200次实验，采用几何法和基于选权迭代抗差估计的历元间差分算法分别进行解算，并分别统计其平均定位精度，如表2所示。

表2 仿真200次几何法和差分法解算平均定位精度

几何法定位的水平精度略优于其垂直精度，这是由于测量船在海面上持续走航，其航迹几乎在一个平面上，垂直方向上的观测结构相对要差一些；对比几何法和历元间差分算法可看出，历元间单差解算结果精度特别是垂直方向上明显比几何法高。由于本次模拟试验的入射角不大，系统误差的影响主要体现在解算结果的垂直精度上，差分算法由于观测值在历元间做差，消除了绝大部分系统误差的影响。

4.2 实测算例分析

本算例数据采用2015年7月易水湖实测数据。易水湖位于河北保定境内，水面面积为27km2，最深处为48.5m。易水湖水质清澈纯净、能见度高，是比较理想的测试区域。

易水湖测试仪器为国产BPS声学定位系统，主要的硬件设备如图7所示。GPS接收机和声速仪如图8所示。测量船在水面连续走航，对应答器不间断观测。各个时刻测量船的位置由船载GPS给出，GPS接收机与换能器通过铁杆连接在一起，如图9所示。

图7 硬件设备图

图8 GPS接收机(a)和声速仪(b)

4.2.1 测线相对位置验证

在水底布设10个应答器成一条测线，相邻应答器间隔约20m。测量换能器从发射至接收声波的时间差，并用声速仪实测声速剖面。测量船航迹及应答器位置如图10所示。

对实测数据预处理之后，分别采用几何法和单差法进行定位解算。由于试验区域水下应答器位置未知，不能直接比较定位结果，统计内符合精度即计算平差参数中误差，如表3所示。

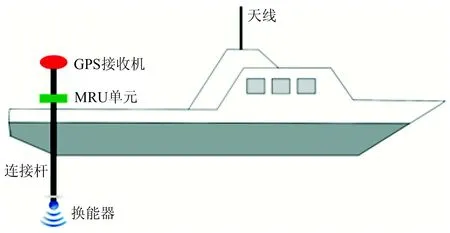
图9 测量船局部放大图

图10 测线验证实验船迹及应答器示意图

表3相对位置验证实验内符合精度单位：m

应答器编号σxσy几何法单差法几何法单差法10．2700．0050．4360．00620．0370．0010．0690．00230．1230．0240．1500．03940．1470．0090．2830．01251．8680．6602．7560．66460．1150．0890．4320．16470．8560．0011．1610．00180．0180．0010．0210．00190．2490．0050．3710．003100．5520．0010．7910．001

根据表3，统计10个应答器水下定位内符合精度可以看出，几何法解算x、y方向内符合精度最大值分别为1.868m和2.756m；差分法解算x、y方向内符合精度最大值分别为0.660m和0.664m，均不超过1m。综合两个方向来看，几何法和差分法水平精度分别为0.535m和0.084m，后者比前者提高了0.451m。

4.2.2 单点绝对位置验证

在水底合适位置布设一个应答器，用连接杆将应答器和GPS接收机竖直连接。用GPS RTK实测该单点的平面坐标作为目标点坐标真值，测量船持续走航对水底应答器连续观测获取观测值，分别用几何法、单差法进行解算，解算结果与坐标真值比对计算平面方向的坐标偏差。测量船航迹及应答器位置如图11所示。表4为单点绝对位置验证所解算的坐标偏差结果。

图11 单点验证实验船迹及应答器示意图

如表4所示，传统几何法平面定位精度为1.186m，差分法定位精度达1.015m，后者采用选权迭代抗差估计对实测数据中不可避免的粗差值予以剔除，保证了数据质量，并通过观测值历元间做差，削弱了与应答器时延及声速等有关的部分系统误差，定位精度提高了17cm。dx差值较大，验证了对单差定位方法而言，应答器与定位船航行的相对空间关系对定位结果的影响明显优于几何法。由于实测区域最大水深为50m，声速相关的系统误差影响并不是特别显著，所以差分法定位精度略优于几何法。但是随着水深增加，与声速等相关的系统误差随之增大，理论上差分法定位优势会愈加明显，这也有待下一步深入研究和试验验证。就目前的水下定位测试结果而言，国产BPS声学定位系统在50m以内水深条件下，走航式水下差分法定位精度达到1m，可满足石油勘探需求。

表4 绝对位置验证实验解算坐标偏差单位：m

5 结论

水下声学差分定位方法自提出以来，受到广泛关注，之前其定位效果多通过模拟数据讨论分析，鲜有实测数据支持。本文在详细推导水下声学单差定位模型的基础上，首次探讨将水下差分定位应用到海上石油勘探过程中，并通过理论分析和实测数据进行验证，得到以下结论：

(1)基于选权迭代的水下声学差分定位算法，在剔除粗差、提高数据质量的基础上，通过历元间观测值差分减弱部分水下定位系统误差和空间相关性误差影响，其定位结果优于传统几何法；

(2)在50m以内水深条件下，自主研发的国产BPS声学定位系统实现1m的定位精度，可满足石油勘探需求。

水声差分定位方法在一定程度上提高了水下定位的精度和可靠性，在石油地球物理勘探(尤其是高精度海上油气勘探)和海洋工程领域有良好的应用前景。此外，更大水深条件下的水声差分算法和国产声学定位系统的性能有待下一步深入研究和试验验证。

[1] 张红梅.水下导航定位技术.湖北武汉：武汉大学出版社，2010.

Zhang Hongmei.Underwater Navigation and Positioning Technology.Wuhan University Press,Wuhan，Hubei,2010.

[2] 杨元喜,徐天河,薛树强.我国海洋大地测量基准与海洋导航技术研究进展与展望.测绘学报，2017，46(1):1-8.

Yang Yuanxi,Xu Tianhe,Xue Shuqiang.Progresses and prospects in developing marine geodetic datum and marine navigation of China.Acta Geodaetica et Cartographica Sinica,2017,46(1):1-8.

[3] Xu Peiliang,Ando M,Tadokoro K.Precise,three-dimensional seafloor geodetic deformation measurements using difference techniques.Earth Planets & Space,2005,57(9):795-808.

[4] Zhao Jianhu,Zou Yajing,Zhang Hongmei et al.A new method for absolute datum transfer in seafloor control network measurement.Journal of Marine Science & Technology,2016,21(2):216-226.

[5] Yang Fanlin,Lu Xiushan,Li Jiabiao et al.Precise positioning of underwater static objects without sound speed profile.Marine Geodesy,2011,34(2):138-151.

[6] 蔡艳辉，杨新红.差分GPS水下定位系统的解析法分析.大地测量与地球动力学，2008，28(6):101-106.

Cai Yanhui,Yang Xinhong.Underwater positioning system’s baseline network analyzing based on analytical method.Journal of Geodesy and Geodynamics,2008,28(6):101-106.

[7] Yan Weisheng,Chen Wei,Cui Rongxin.Moving long baseline positioning algorithm with uncertain sound speed.Journal of Mechanical Science and Technology,2015,29(9):3995-4002.

[8] 周江文.经典误差理论与抗差估计.测绘学报，1989,18(2):115-120.

Zhou Jiangwen.Classical theory of errors and robust estimation.Acta Geodaetica et Cartographic Sinica,1989,18(2):115-120.

[9] Yang Yuanxi,Song Lijie,Xu Tianhe.Robust estimator for correlated observations based on bifactor equivalent weights.Journal of Geodesy,2002,76(6-7):353-358.

[10] Xu Peiliang.Sign-constrained robust least squares,subjective breakdown point and the effect of weights of observations on robustness.Journal of Geodesy,2005,79(1-3):146-159.

[11] 王潜心，徐天河，许国昌.粗差监测与抗差估计相结合的方法在动态相对定位中的应用.武汉大学学报(信息科学版)，2011,36(4):476-480.

Wang Qianxin,Xu Tianhe,Xu Guochang.Application of combining method of outlier detection and robust estimation to GPS kinematic relative positioning.Geomatics and Information Science of Wuhan University,2011,36(4):476-480.

[12] 张志伟，暴景阳，肖付民等.抗差估计在多波束测深异常值探测中的应用.辽宁工程技术大学学报(自然科学版),2016，35(7):755-758.

Zhang Zhiwei,Bao Jingyang,Xiao Fumin et al.Application of robust estimation for detecting outliers of multibeam data.Journal of Liaoning Technical University(Natural Science),2016,35(7):755-758.

[13] 方守川，秦学彬，任文静等.基于多换能器的声学短基线海底电缆定位方法.石油地球物理勘探,2014,49(5):825-828.

Fang Shouchuan,Qin Xuebin,Ren Wenjing et al.Ocean buttom cable positioning based on multi-transducer short baseline acoustic method.OGP,2014,49(5):825-828.

[14] 易昌华，任文静，王钗.二次水声定位系统误差分析.石油地球物理勘探,2009,44(2):136-139.

Yi Changhua,Ren Wenjing,Wang Chai.Analysis on error of secondary acoustic positioning system.OGP,2009,44(2):136-139.

[15] 蔡艳辉，程鹏飞，王权.水下GPS系统的稳定性分析.测绘科学，2012，37(5):30-32.

Cai Yanhui,Cheng Pengfei,Wang Quan.Stability analysis on underwater GPS positioning system.Science of Surveying and Mapping,2012,37(5):30-32.

[16] 赵建虎，刘经南.多波束测深及图像数据处理.湖北武汉：武汉大学出版社,2008.

Zhao Jianhu,Liu Jingnan.Multi Beam Sounding and Image Data Processing.Wuhan University Press,Wuhan,Hubei,2008.

[17] Yamada T,Ando M,Tadokoro K et al.Error evaluation in acoustic positioning of a single transponder for seafloor crustal deformation measurements.Earth Planets and Space,2002,54(9):871-882.

[18] Spiess F N,Chadwell C D,Hildebrand J A et al.Precise GPS/acoustic positioning of seafloor reference points for tectonic studies.Physics of the Earth and Planetary Interiors,1998,108(2):101-112.

[19] 杨元喜.抗差估计理论及其应用.北京：八一出版社,1993.

Yang Yuanxi.The Theory and Application of Robust Estimating.Bayi Press,Beijing,1993.

[20] Yang Y X.Robust estimation for dependent observation.Manuscripta Geodactica,1994,19(1):10-17.

[21] 杨元喜.等价权原理——参数平差模型的抗差最小二乘解.测绘通报，1996,49(6):33-35.

Yang Yuanxi.The principle of equivalent weight—The least squares robust estimation of parameter adjustment model.Bulletin of Surveying and Mapping,1996,49(6):33-35.

[22] 陆基孟等.地震勘探原理.北京：石油工业出版社，1982.

[23] 易昌华，韩华，方守川等.海上地震勘探罗经鸟数据对拖缆空间位置的影响．石油地球物理勘探,2015,50(5):809-814.

Yi Changhua,Han Hua,Fang Shouchuan et al．Compass data influence on towed streamer positioning in marine seismic.OGP,2015,50(5):809-814.

[24] 王振杰，李圣雪，聂志喜等.水声定位中一种大入射角声线跟踪方法.武汉大学学报(信息科学版),2016,41(10):1404-1408.

Wang Zhenjie,Li Shengxue,Nie Zhixi et al.A large incidence angle ray-tracing method for underwater acoustic positioning.Geomatics and Information Science of Wuhan University,2016,41(10):1404-1408.

[25] 张居成.深水长基线定位导航技术研究[学位论文].黑龙江哈尔滨：哈尔滨工程大学,2014.

[26] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础.湖北武汉：武汉大学出版社，2003.

Surveying Adjustment Department of School of Geodesy and Geomatics of Wuhan University.Error Theory and Fundation of Surveying Adjustment.Wuhan University Press,Wuhan,Hubei,2003.

*山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院测绘系，266580。Email: sd_zhaoshuang@126.com

本文于2016年10月27日收到，最终修改稿于2017年10月10日收到。

本项研究受国家重点研发计划项目(2016YFB0501700，2016YFB0501705)、国家自然科学基金项目(41374008，41406115)、国家科技支撑计划项目(2014BAK11B01)联合资助。

1000-7210(2017)06-1137-09

赵爽，王振杰，吴绍玉，王毅，刘慧敏，单瑞.基于选权迭代的走航式水声差分定位方法.石油地球物理勘探，2017,52(6):1137-1145.

P631

10.13810/j.cnki.issn.1000-7210.2017.06.002

(本文编辑：刘英)