常规公交车辆串车形成及预测建模
2017-12-18李梦甜李文权
张 健 李梦甜 冉 斌 李文权
(1东南大学城市智能交通江苏省重点实验室, 南京 210096)(2东南大学现代城市交通技术江苏高校协同创新中心, 南京 210096)(3东南大学江苏省物联网技术与应用协同创新中心, 南京 210096)(4东南大学物联网交通应用研究中心, 南京 210096)
常规公交车辆串车形成及预测建模
张 健1,2,3,4李梦甜1,2,3,4冉 斌1,2,3,4李文权1,2
(1东南大学城市智能交通江苏省重点实验室, 南京 210096)(2东南大学现代城市交通技术江苏高校协同创新中心, 南京 210096)(3东南大学江苏省物联网技术与应用协同创新中心, 南京 210096)(4东南大学物联网交通应用研究中心, 南京 210096)
首先结合车头时距不稳定性的概念,对串车现象给出判定依据;分析串车问题产生的6种典型过程,建立串车问题数学模型,对串车发生的原因进行理论分析.然后,以自贡市38路公交线路实际数据为例,采用方差分析与回归分析筛选出7个串车形成影响因素,并对其重要性进行排序.最后,建立基于径向基函数神经网络的串车问题预测模型,对未来站的车头时距进行预测,并选取自贡市38路公交车的实时数据进行模型验证.在38 000余组数据中随机选择300组数据进行训练, 对比30组测试数据. 结果表明,学习得到的预测值与实际值偏差10%以内的样本点占90%,结果良好,证明了所建立的模型具有较好的适用性.
公共交通;串车;排序;径向基函数神经网络
随着城镇化进程加快,城市交通供需不平衡矛盾日益突出,交通拥堵已成为严重制约我国城市健康可持续发展和居民生活水平进一步提高的主要原因之一.城市常规公共交通作为有效缓解交通拥堵的出行方式之一,以其价格低廉、资源高效利用,而得到大力提倡.大力优先发展城市公共交通已成为国策.如何进一步提升城市常规公交服务水平,具有紧迫的现实意义和较好的理论研究价值.Joshua[1]研究表明,乘客感受到的公共交通服务水平取决于公共交通系统运行的稳定性.由于对外部干扰的敏感性,公交车辆在运行过程中会产生诸如串车等一系列问题.
根据控制基准点不同,国外将串车问题的研究方法分为3类[2]:基于时刻表、基于车头时距和基于实时信息的串车问题.Rufi[3]利用公交车在车站的到达时间、离开时间、停站时间、上下车人数以及线路的基础数据,搭建微观交通仿真平台,建立了线路公交车仿真模型.Delgado等[4]认为,控制策略法虽缓解了串车问题,但使车辆运行速度下降,因而提出了驾驶员可通过控制登车人数以提高车辆运行速度的方法,并研究了同时采用控制方法和控制登车人数更优的情况.Chen等[5]提出建立在多个控制点的控制策略,并考虑到采用控制方法时乘客的上下车问题.Bartholdi等[6]放弃传统时刻表甚至预先设定目标车头时距的概念,分别采用控制车头时距收敛速度和车头时距下限,以加强平衡性.通过调整参数,增加或减少一辆多余的公交车,系统将会自行通过目标车辆和前后车距离调整速度.
国内对串车问题的研究起步较晚.董高成等[7]针对串车现象,基于行车路线区间划分以及路段调节能力提出了快速公共交通的实时行车控制方法.刘明卉[8]定性分析串车现象的主要产生原因,并提出基于甩站策略的公交车控制模型.徐茹[9]提出了串车的定性定义,认为车辆间隔距离与车速有一定关系,并在微观分析的基础上建立了基于车辆间隔距离的反馈控制模型.此外,Zhang等[10]通过对站点停靠位置通行能力和实际公交车定位数据的分析,以及控制车辆的停靠时间和发车间隔的波动有效地解决了串车问题.杨敏等[11]将差分自回归移动平均模型和支持向量机方法进行组合构建了一种快速公交停站时间的组合预测方法.Yin等[12]提出了一种驻站和甩站组合的混合实时站点控制策略.目前在串车的研究中,串车现象的判定以及产生原因均以定性描述为主,缺乏定量的判断依据.本文基于公交车实际实时数据,给出串车问题定量判定方法和理论分析,从而对串车问题进行有效预测.
1 串车现象判断及典型过程
1.1 现象判断
车头时距的不稳定性是造成串车的重要原因[12],用指标Ccov(h)来表示车头时距不稳定性,其计算式为
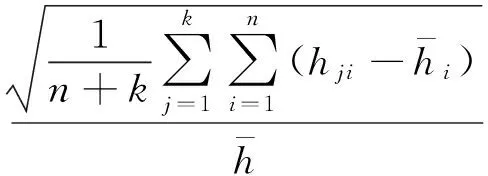
(1)

1.2 典型过程
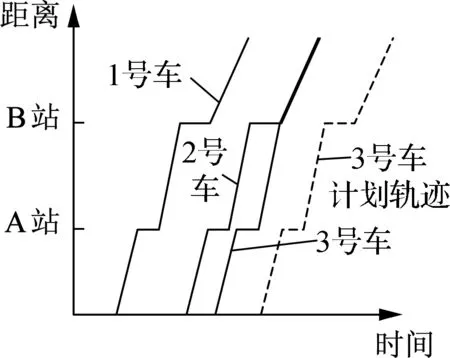
串车现象共有6种典型过程,图1通过公交车的时空轨迹图进行描述.横坐标表示公交车运行时间,纵坐标表示公交车距离出发点的距离,斜率表示公交车平均运行速度.假设根据行车计划,编号为1,2,3的公交车按照相同车头时距发车,每辆公交车在受到干扰前都保持相同的运行速度.
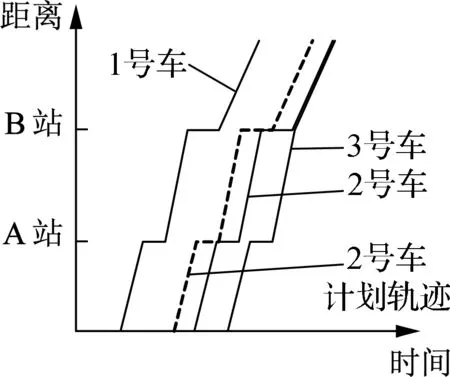
(a) 2号车晚于计
途中受到干扰
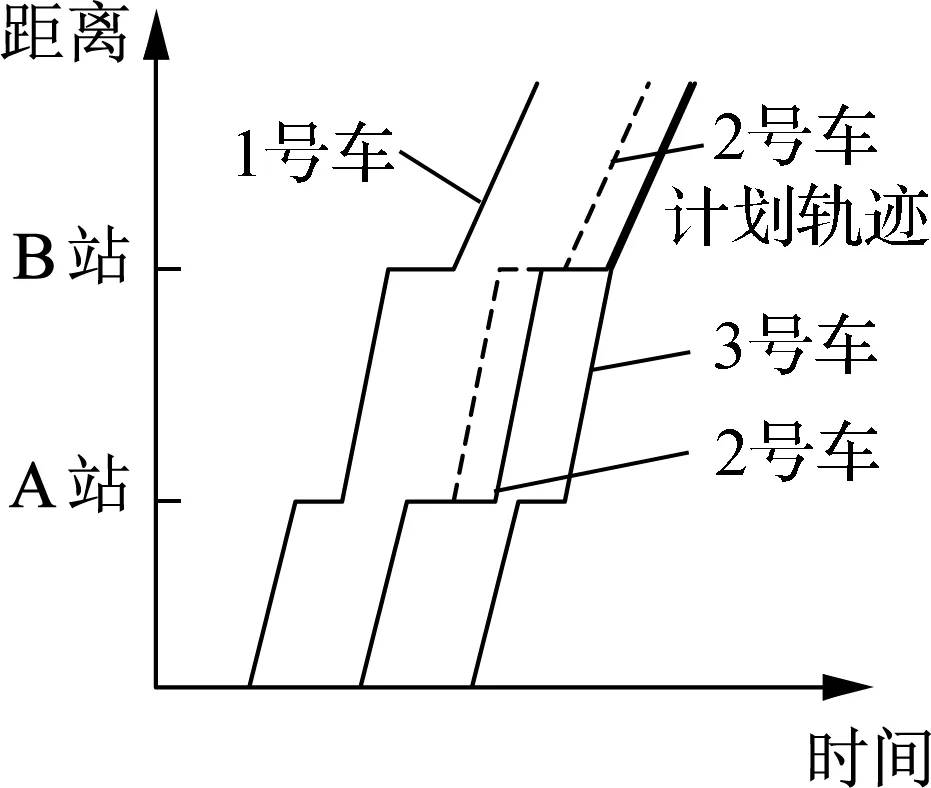
(c) 2号车停站时间过长
计划发车时间
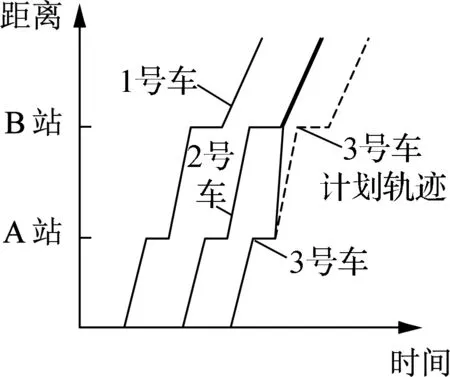
(e) 3号车在AB站间
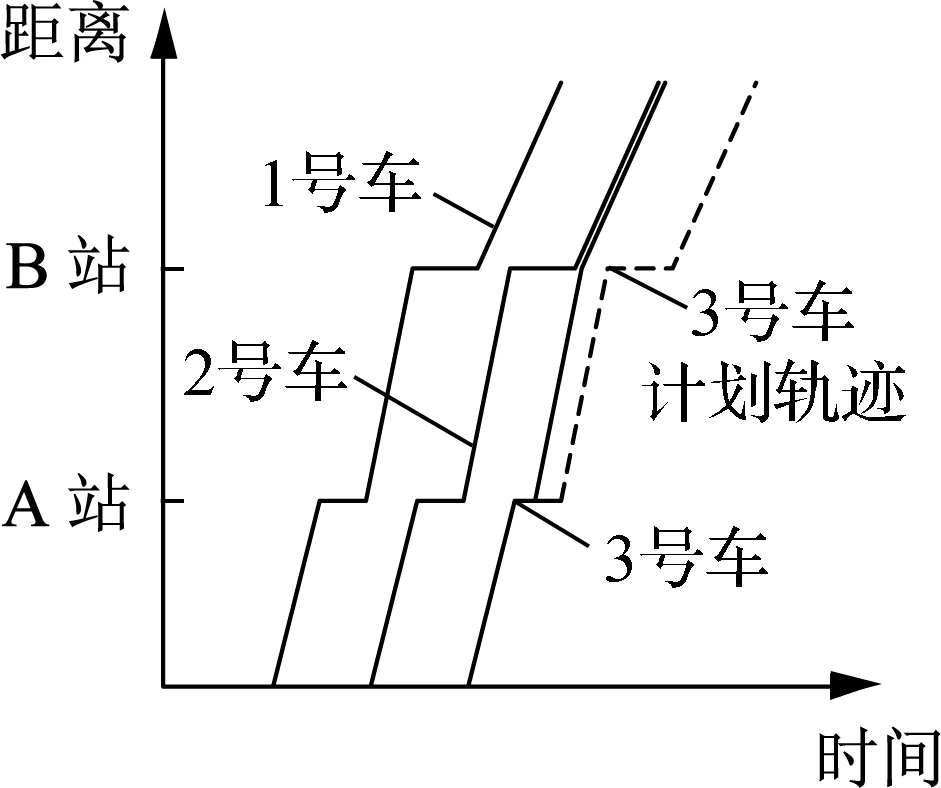
(客流锐减)
图1串车典型过程的公交车时空轨迹图
2 串车现象理论模型及原因分析
2.1 模型假设
将基于时刻表的行车间隔记为理想车头时距,串车现象就是车头时距远大于理想车头时距;大间隔现象就是车头时距远小于理想车头时距(与串车现象相对应).为建立模型,做如下假设:① 公交车辆在始发站及终点站不进行发车间隔调整,线路抽象为连续、闭合的圈点图,且站间距相同.② 车辆启停时间忽略不计,即停站总时间由乘客登车总时间决定.③ 乘客到达时间满足时间上的相互独立,空间上均匀分布,且就近候车,登车总时间与乘客人数成正比.④ 目标车辆在目标站点的前一站为理想平衡状态,目标车辆的前一车辆在目标站点保持理想平衡状态.
2.2 模型建立步骤
1) 满足以下条件时称为达到平衡条件:
① 线路上共有M个公交站点,乘客以平稳速率到达第m站点(m=1,2,…,M),即速率αm为定值;② 乘客均匀分布在各站点,且到达率相同(车站聚集人数与时间成正比);③ 第n辆车的区间运行速度相同,即运行速度vn为定值;④ 第m站、第n辆车与前车的车头时距Hm,n与平衡条件下的发车间隔H相等,即Hm,n=H;其中,以定量表述线路上前后相邻2车之间的行车间隔称为车头时距.
2) 成因分析模型计算
在假定的理想状态下,当线路总长为L,站间距为D=L/(m-1)时,车辆从第(m-1)站离站到第m站离站,所需总旅行时间包括乘客相互独立的区间运行时间D/vn和乘客数量相关的累积登车时间(即停站时间)αmHm,nβ.其中,vn为区间运行速度,D为站间距,Hm,n为车头时距,αm为乘客到达率,β为乘客人均登车时间.
① 第m站、第n辆车的离站时刻
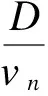
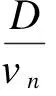
(2)
式中,Tm,n为第m站、第n辆车的总等车时间(即停站时间).
② 第m站、第n辆车的离站车头时距
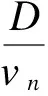
(3)
整理式(3),可得
αmHm,(n-1)β
(4)
进一步整理,可得
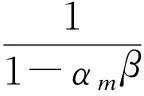
(5)
式(5)还可表示为
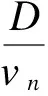
(6)
2.3 模型分析
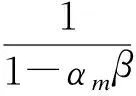
同时,式(5)可以转化为
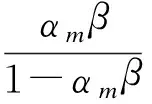
(7)
由式(6)可以得出,第m站、第n辆车与前车的车头时距与第(n-1)辆车在本站与前车的车头时距负相关,第m站、第n辆车与前车的车头时距与第(n-1)辆车与第n辆车的速度差正相关(见图1(b)).此外,由式(5)可以得出:第m站、第n辆车与前车的车头时距与其在本站的停站时间正相关(见图1(c));第m站、第n辆车与前车的车头时距与第(n-1)辆车在本站的停站时间负相关(见图1(d));第m站、第n辆车与前车的车头时距与其区间运行时间正相关;第m站、第n辆车与前车的车头时距与第(n-1)辆车的区间运行时间负相关.
根据系统建模计算的结果可知,串车现象具有传递性、放大性等性质,同时可以分析出造成串车问题的原因可能是:目标车辆提前离站、前车停站延误、本车区间运行超速以及前车区间运行延误.除此之外,由于实际路网中的情况相对复杂,可能会出现上述4种情况的不同组合模式.
3 串车现象预测及案例
3.1 串车现象影响因素
由式(1)可知,系统不稳定性由车头时距决定,因此将对系统不稳定性的影响因素的研究转换为对车头时距的影响因素进行分析,后车的进(出)站时间与前车的进(出)站时间差值就是车头时距.可能影响车头时距的因素包括车站属性、车辆属性、行驶时间(段)、区间旅行时间、前车区间旅行时间、停站时间、前车停站时间、发车间隔等.其中时间因素可简化为:早高峰前、早高峰、非高峰1(2 h)、非高峰2(2 h)、非高峰3(2 h)、非高峰4(2 h)、晚高峰(2 h)和晚高峰后.
方差分析从观测变量的方差入手,研究诸多控制变量中哪些变量是对观测变量有显著影响.回归分析是确定2种或2种以上变量间相互依赖的定量关系的一种统计分析方法.下面分别采用方差分析与回归分析方法对影响因素进行筛选和排序.
3.2 因素分析
3.2.1 数据说明
自贡是川南区域中心城市,为四川省辖地级市.本文选取了自贡市2014年10月期间,38路公交车的38 000余组数据进行研究,该线路运行总里程为10.5 km,运行时间为6:30—21:00,共计停靠24个站点,发车间隔2~7 min,首末站分别为翰林尚都站和沙鱼坝站.由于38路纵穿自贡市,途径大安区政府、自贡市第四人民医院等多个城市重要节点,交通干扰较多,易出现串车等现象.为了确保数据的准确性和研究的严谨性,将剔除线路上的招呼站、虚站总共6个车站,选取剩余18个车站作为研究对象.其中主要时间因素点包括早高峰前(7:00以前)、早高峰(7:01—9:00)、非高峰1(9:01—11:00)、非高峰2(11:01—13:00)、非高峰3(13:01—15:00)、非高峰4(15:01—17:00)、晚高峰(17:01—19:00)、晚高峰后(19:00以后).
3.2.2 因素筛选
方差分析着重于观测变量取值的变化受到不同水平控制因素(即控制变量)以及随机因素(即随机变量)2个方面的影响.其中,随机因素主要来源于随机误差.该方法认为,如果控制变量发生显著变化,观测变量同时产生显著变化,则可认为观测变量同时受到控制变量和随机变量的影响,否则可认为观测变量仅受到随机变量的影响.
本文中观测变量为车头时距;控制变量为车站编号、车辆编号、时间段、区间旅行时间、前车区间旅行时间、停站时间、前车停站时间、发车间隔,共8个控制变量.提出零假设,即各控制变量不同水平下观测变量各总体的均值无显著差异,选取显著性水平α为0.05.
车站编号、车辆编号、时间段、区间旅行时间、停站时间、前车停站时间、发车间隔均小于显著性水平,对车头时距有显著影响;前车旅行时间的F检验统计量的概率p值为0.587,大于显著性水平,不能拒绝原假设,因此其被排除.
3.2.3 因素权重排序
以上选取的控制变量分为分类型变量(车站编号、车辆编号、时间段)与数值型变量(区间旅行时间、停站时间、前车停站时间、发车间隔).首先利用线性回归模型对数值型变量(定距)发车间隔、停站时间、前车停站时间、区间旅行时间进行建模和检验分析,得到如下方程:
Y=109.519+0.587X1+0.598X2-0.371X3+0.055X4
(8)
式中,X1,X2,X3,X4分别为发车间隔、停站时间、前车停站时间、区间旅行时间.但是,方程的拟合优度R2=0.206,拟合优度并不高,所以线性回归方程仅作为参考,不能直接进行预测和分析.
此外,考虑到解释变量中既有数值型变量,又有分类变量,既有定距变量,又有定序变量,故进一步选用回归分析方法时,采用SPSS软件中自动线性建模方式进行建模.学生化残差的直方图(见图2)表明,残差分布与均值为0的正态分布基本吻合,则自动线性回归模型可靠,输入样本量N=40 639;标准差为1.0,目标为进站车头时距.利用学生化残差的直方图将残差分布与正态分布相比较,图2中平滑线表示正态分布,残差频数越靠近平滑线,则残差分布越接近于正态分布.
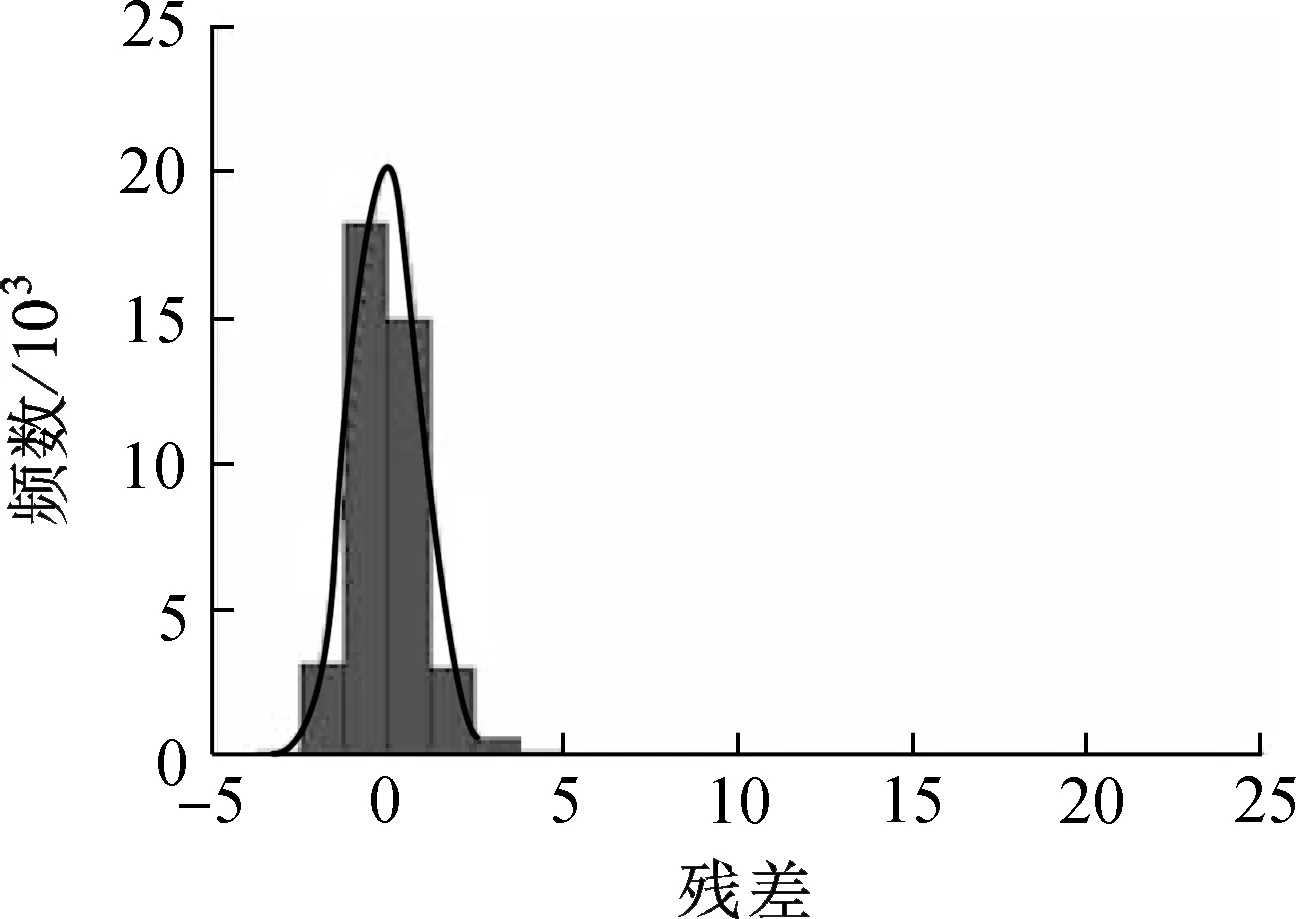
图2 自动线性模型的残差正态性分析

图3 自动线性模型中预测变量重要性排序
3.3 预测分析
3.3.1 公交车串车预测模型
本文中串车现象预测采用RBF径向神经网络,将3.2节中对车头时距有显著影响的7个变量作为RBF径向神经网络的输入变量,分别为发车间隔X1、停站时间X2、前车停站时间X3、区间旅行时间X4、车辆编号X5、时间段X6和车站编号X7,将该车辆下一站车头时距Y1设为输出变量,建立7-15-1网络结构,即7个输入层节点、15个隐含层节点和1个输出层节点.
3.3.2 公交车串车预测模型
随机选取300组数据作为训练集,30组数据作为测试集,分别计算出发车间隔、停站时间、前车停站时间、区间旅行时间、车辆编号、时间段和车站编号,并计算出本站车头时距.将所有计算结果以车辆编号为筛选字段,离站时间为排序字段排序,从而得到下一站的车头时距.
利用Excel对所有历史数据进行数据处理,得到历史数据源.利用Matlab软件随机选取300组数据作为原始数据进行网络学习,得到基于RBF神经网络预测模型实际值与预测值对比图(见图4).
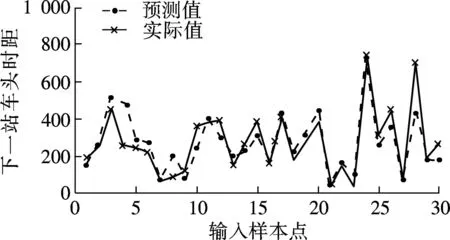
图4 基于RBF神经网络预测模型输出曲线图
由图4可见,30个样本点中预测值与实际值偏差在10%以内的样本点占90%,拟合效果较好,基本可以体现出串车问题的发生点与问题严重程度.因此,基于RBF神经网络预测模型具有较好的预测价值.
4 结语
采用理论模型和基于真实数据的实例分析相结合的方式,列举了串车的6种典型过程,系统地分析了导致串车发生的影响因素和形成原因,筛选出7个因素,按照重要性大小排序为发车间隔、时间段、停站时间、前车停站时间、区间旅行时间、车站编号、车辆编号.最后,通过RBF径向神经网络模型,实现了对公交车辆串车问题有效的预测.
研究中未能对其他可能影响因素(如天气、驾驶员驾驶习惯等)进行筛选,RBF径向神经网络的收敛速度也较慢,预测实时性较差,这些将在后续研究中深入讨论分析.
基于此,本研究通过实地与网上两种形式对居民厕纸使用后的处理方式进行调查,并根据调查结果进行统计分析,了解人们对厕纸的处理习惯及厕纸处置现状.为探究两种方式对环境的影响,采用实验室模拟的方式,测定厕纸置于水中后不同时间产生的化学需氧量(COD)、悬浮物(SS)、氨氮、五天生化需氧量(BOD5),得到厕纸进入下水道对污水处理厂的污染物贡献值;另一方面为了分析将厕纸作为固废处理会对环境产生怎样的污染情况,采用客观的统计数据和科学的研究实验,最后通过分析结果与实验监测等得出的数据作为依据,正确地回答了“如何处理厕纸更符合节能环保理念”的问题.
)
[1] Joshua M P. An approach to reducing bus bunching [D]. Berkeley, CA, USA: University of California, 2009.
[2] Zolfaghari S, Azizi N, Jaber M Y. A model for holding strategy in public transit systems with real-time information [J].InternationalJournalofTransportManagement, 2004,2(2): 99-110. DOI:10.1016/j.ijtm.2005.02.001.
[3] Rufi F M. Optimization analysis of the number and location of holding control stops to prevent bus bunching [D]. Stockholm, Sweden: Kungliga Tekniska Hogskolan, 2011.
[4] Delgado F, Munoz J C, Giesen R. How much can holding and/or limiting boarding improve transit performance? [J].TransportationResearchPartB, 2012,46(9): 1202-1217. DOI: 10.1016/j.trb.2012.04.005.
[5] Chen Q, Adida E, Lin J. Implementation of an iterative headway-based bus holding strategy with real-time information [J].PublicTransport, 2012,4(3): 165-186. DOI:10.1007/s12469-012-0057-1.
[6] Bartholdi J J, Eisenstein D D. A self-coordinating bus route to resist bus bunching [J].TransportationResearchPartB, 2012,46(4): 481-491. DOI: 10.1016/j.trb.2011.11.001.
[7] 董高成,张海,沈晓蓉,等.基于区段划分的快速公交实时行车控制研究[J].系统仿真技术,2012,8(1):16-22,50. DOI: 10.3969/j.issn.1673-1964.2012.01.004.
Dong Gaocheng, Zhang Hai, Sheng Xiaorong, et al. BRT real-time control based on bus-line partition[J].SystemSimulationTechnology, 2012,8(1): 16-22, 50. DOI: 10.3969/j.issn.1673-1964. 2012.01.004. (in Chinese)
[8] 刘明卉.基于甩站策略的城市公交服务可靠性研究[D].北京:北京邮电大学经济管理学院,2012.
[9] 徐茹.公共交通运力配置最优化问题研究[D].北京:北京工业大学软件学院,2013.
[10] Zhang Man, Li Wenquan. Factors affecting headway regularity on bus routes [J].JournalofSoutheastUniversity(EnglishEdition), 2013,29(1): 99-102. DOI: 10.3969/j.issn.1003-7985. 2013. 01. 020.
[11] 杨敏,丁剑,王炜.基于ARIMA-SVM模型的快速公交停站时间组合预测方法[J].东南大学学报(自然科学版),2016,46(3):651-656. DOI: 10.3969/j.issn.1001-0505. 2016. 03.033.
Yang Min, Ding Jian, Wang Wei. Hybrid dwell time prediction method for bus rapid transit based on ARIMA-SVM model[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2016,46(3): 651-656. DOI: 10.3969/j.issn.1001-0505.2016.03.033. (in Chinese)
[12] Yin T T, Zhong G, Zhang J, et al. A hybrid real-time bus control strategy with a multi-criterion evaluation[C]//Proceedingsofthe16thCOTAInternationalConferenceofTransportationProfessionals. Shanghai, China, 2016: 681-691. DOI: 10.1061/9780784479896.063.

Causesandforecastmodelingofconventionalbusbunching
Zhang Jian1,2,3,4Li Mengtian1,2,3,4Ran Bin1,2,3,4Li Wenquan1,2
(1Jiangsu Key Laboratory of Urban ITS, Southeast University, Nanjing 210096, China) (2Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies, Southeast University, Nanjing 210096, China) (3Jiangsu Province Collaborative Innovation Center for Technology and Application of Internet of Things, Southeast University, Nanjing 210096, China) (4Research Center for Internet of Mobility, Southeast University, Nanjing 210096, China)
First, based on the concept of vehicle headway instability, the criterion for bus bunching phenomenon is proposed. By analyzing the six typical processes of the bus bunching problem, a mathematical model is established, with which the theoretical factors of bus bunching are analyzed. Then, taking the actual data of No.38 bus route in Zigong city for example, seven influencing factors are selected by using variance analysis and regression analysis, and are sorted by the importance. Finally, a forecasting model of the bus bunching problem based on radial basis function (RBF) neural network is established to forecast the headway of the future station. The real-time data of No. 38 bus route in Zigong city are employed to validate the proposed model. The 300 groups of data randomly selected from more than 38 000 groups of real data are used for training. By comparing 30 sets of test data, the results show that the samples with the errors between predicted and actual values within 10% account for 90%, which illustrate the result is good. It is proved that established model has good applicability.
public transit; bus bunching; sort; radial basis function (RBF) neural network
10.3969/j.issn.1001-0505.2017.06.029
U492.3
A
1001-0505(2017)06-1269-05
2017-03-24.
张健(1984—),男,博士,讲师,jianzhang@seu.edu.cn.
国家重点研发计划资助项目(2016YFB0100906)、国家自然科学基金资助项目(61620106002,51308115).
张健,李梦甜,冉斌,等.常规公交车辆串车形成及预测建模[J].东南大学学报(自然科学版),2017,47(6):1269-1273.
10.3969/j.issn.1001-0505.2017.06.029.
