基于虚拟惰性点的土基模量反演方法

臧国帅 孙立军 陈 长

(同济大学道路与交通工程教育部重点实验室, 上海 201804)

基于虚拟惰性点的土基模量反演方法

臧国帅 孙立军 陈 长

(同济大学道路与交通工程教育部重点实验室, 上海 201804)

为了提高惰性点法土基模量反演精度,研究了基于有限点弯沉的完整弯沉盆的预测方法,提出了基于预测完整弯沉盆的虚拟惰性点计算方法,并与基于实际完整弯沉盆的实际惰性点的反演结果相对比,针对反演精度进行了理论分析和实例验证.结果表明,分别采用对数分段线性插值法和指数模型预测弯沉检测范围内、外的弯沉盆信息时,预测精度高,计算简便.实惰性点法和虚惰性点法的平均理论反演误差分别为1.70%和1.53%.惰性点位置对反演误差有较大影响,当惰性点位置超出弯沉盆检测范围时,实惰性点法和虚惰性点法的平均反演误差分别为2.63%和1.45%.实测弯沉盆分析结果与理论模拟分析结果相符.通过改进惰性点参数计算方法,虚惰性点法显著提高了土基模量反演精度.

沥青路面;惰性点;弯沉盆曲线;落锤式弯沉仪;模量反演

基于落锤式弯沉仪(falling weight deflectometer,FWD)检测的弯沉盆反演路面结构模量是路面结构承载能力评估的重要指标.模量反演方法可以大致分为弯沉盆匹配法和弯沉盆规律2类[1].弯沉盆匹配法的基本原理是采用迭代试算方法来匹配实测弯沉盆和理论弯沉盆,即采用蚁群算法、遗传算法、人工神经网络算法等使目标函数最小[2].弯沉盆规律法的基本原理是从弯沉盆本身受结构参数影响的规律出发,找到具有特殊意义和规律性较强的点来反演结构各层模量.孙立军等[3]发现在水泥混凝土路面中存在惰性弯沉点,将其用于反演水泥混凝土路面结构模量,该方法收敛且解唯一,精度和效率均较高.Zhang等[4]验证出惰性弯沉点也存在于沥青路面弯沉盆中.朱洁等[5]提出了一种基于均方根误差最小原则的沥青路面惰性弯沉点选取方法.

模量反演的首要前提是已知路面完整弯沉盆信息.然而,受限于设备造价和检测效率,常用的FWD设备仅能检测出有限个位置处的弯沉,且最远弯沉检测位置约为2.4 m,无法测得整个弯沉盆信息.当结构层厚度较大而土基模量较小时,路面弯沉盆的影响范围可能距离荷载中心点以外4 m以上.对于弯沉盆匹配法来说,采用的是不完整的弯沉盆信息;对于惰性弯沉规律来说,检测弯沉范围可能没有覆盖惰性点.因此,在模量反演之前,应当首先利用实测的有限点弯沉来预估路面完整弯沉盆信息.本文采用插值和拟合相结合的方法来预估路面完整弯沉盆信息,即分别采用了插值法和拟合回归函数来预估FWD检测范围内、外的弯沉盆信息.然后,分析了此方法对惰性点参数和土基模量反演精度的影响.

1 惰性点法土基模量反演原理

惰性弯沉点具有2个参数,即惰性弯沉点至荷载中心距离Rc和相应的弯沉Dc.惰性点参数只与路面总厚度H和土基模量E0有关,即

Rc=f(H,E0),Dc=g(H,E0)

(1)

对于某一FWD实测弯沉盆,其对应的路面总厚度H已知,则式(1)可转化为

Rc=f(E0),Dc=g(E0)

(2)

由式(2)可知,Rc和Dc均与E0成一一对应关系,因此存在着如下隐式的惰性点参数函数关系:

Dc=h(Rc)

(3)

图1为惰性点法示意图.由图可知,当E0增大时,Rc逐渐靠近荷载中心点,使惰性点位置处的Dc逐渐减小,而FWD弯沉随之增大.当惰性点弯沉与FWD弯沉相等时,便可得到土基模量反演值.

图1 惰性点法示意图

由此可知,惰性点法反演土基模量的关键是基于有限点弯沉预测完整弯沉盆信息以及惰性点参数回归方程.

2 完整弯沉盆预测模型

常用的FWD设备仅能检测有限位置处的弯沉,并未测得整个弯沉盆信息,需要基于有限点弯沉预测完整弯沉盆信息.

根据文献[6-7],列出对FWD弯沉盆拟合效果较好的曲线模型(见表1).常用的插值法有分段线性插值、牛顿插值、三次样条插值等.插值法经过已知测点,而曲线拟合方法不经过已知测点,因此对弯沉检测范围内、外分别采用插值法和曲线拟合外延方法进行弯沉预测.

表1 弯沉盆拟合曲线模型

以一个典型路面结构来举例说明表1中各曲线模型的预测效果.路面结构参数取值如下:面层分为上、中、下3层,厚度分别为4,6,8 cm,模量分别为6 000,4 500,3 000 MPa,泊松比均为0.25;基层厚度为32 cm,模量为10 GPa,泊松比为0.2;在土基顶面以下550 cm[8]处设置刚性下卧层,模量取值为6 894 MPa[9-10],泊松比为0.2.

采用弹性层状体系进行弯沉计算,弯沉计算点位置有9个,间隔为30 cm,径向距离分别为0,30,60,90,120, 150,180,210,240 cm,对应弯沉计算结果分别为141,108,96.8,84.9,73.2,62.3,52.5,43.8,36.2 μm

2.1 曲线拟合模型

多项式曲线对弯沉检测范围内的弯沉预测效果较好,当对弯沉检测范围外的弯沉进行预测时,预测弯沉可能为负值.因此,仅采用表1中其余3种曲线模型进行弯沉盆数据拟合,拟合结果见表2.基于模型回归结果对径向距离500 cm范围内的弯沉进行预测,采用均方根相对误差(RMSE)来表征预测结果与理论弯沉盆的吻合程度,结果见表2.

表2 曲线模型拟合结果与预测结果

注:R2为相关系数.

由表2可知,二次分式曲线的拟合效果较差,指数模型的拟合效果最好;指数型曲线的预测效果最差,指数和二次分式曲线预测效果较好.指数模型可以通过对数变换化为线性模型,模型易于求解.因此,本文选取指数曲线模型进行弯沉盆拟合,用于对有限点弯沉信息进行外延.

2.2 插值法

不同插值法的预测效果见表3.由表可知,三次样条插值法的插值效果最好,对数分段线性插值法次之,牛顿插值插值法效果最差.鉴于三次样条插值计算复杂,本文选取对弯沉取对数后进行分段线性插值的方法.

表3不同插值方法的RMSE对比%

拟合方法并不经过已知点,而插值方法则经过已知点.为了保证用插值法和拟合回归函数来预估FWD检测范围内、外的弯沉盆信息时预测弯沉盆在最外侧检测弯沉处连续,对拟合函数值按照下式进行修正,使得其经过最外侧观测弯沉wout:

(4)

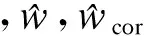
3 虚惰性点法理论反演精度分析

进行土基模量反演时,需基于有限点弯沉预测得到完整弯沉盆信息.如果在进行惰性点参数方程回归时,惰性点参数的计算也是基于限点弯沉预测得到的完整弯沉盆信息,可能会消除反演方法部分系统误差,提高土基模量反演精度.此时得到的惰性点为虚拟惰性点,反演方法记为虚惰性点法.而基于实际完整弯沉盆得到的惰性点为实际惰性点,反演方法记为实惰性点法.分别回归确定这2种方法的惰性点参数方程,进行土基模量反演,对比二者的理论反演精度.

3.1 惰性点参数方程回归

惰性点参数是路面结构厚度和土基模量的函数.惰性点参数的计算需变化结构层厚度组合或模量组合.路面结构层厚度取值范围为20～80 cm,土基模量取值范围为30～300 MPa,面层模量取值范围为1～10 GPa,基层模量取值范围为1.5～15 GPa.共得到5 691个惰性点参数.

采用Table Curve 3D三维曲线拟合软件对惰性点参数数据进行回归分析.该软件内置了大量回归模型,可以实现对三维数据的自动拟合,筛选出回归精度较高的回归模型.本文采用下式来拟合惰性点位置和弯沉方程:

Rc=b1+b2H+b3lnE0+b4H2+b5(lnE0)2+

b6HlnE0+b7H3+b8(lnE0)3+

b9H(lnE0)2+b10H2lnE0

(5)

Dc=c1+c2H-1+c3lnE0+c4H-2+

c5(lnE0)2+c6H-1lnE0+c7H-3+

c8(lnE0)3+c9H-1(lnE0)2+c10H-2lnE0

(6)

式中,b1,b2,…,b10和c1,c2,…,c10均为回归系数.

模型参数回归结果见表4.由表可知,惰性点参数的相关系数均接近于1,表明拟合效果很好.

表4 惰性点参数回归参数

3.2 土基模量理论反演精度分析

3.2.1 理论模拟弯沉盆

路面结构层数设置为5层,即上面层、中面层、下面层、基层和土基.用于生成测试弯沉盆的路面结构的结构层数取5层.厚度取值范围为20～70 cm,取值间隔为5 cm.上、中、下面层厚度均取总厚度的1/9,基层厚度取总厚度的2/3.面层模量取值组合为3组,上、中、下面层模量分别为6.0,4.5,3.0 GPa或4.0,3.0,2.0 GPa或2.5,2.0,1.5 GPa.基层模量在2,6,10,15 GPa中取值.土基模量取值为70～250 MPa,按均匀分布随机生成.总共得到6 600个测试路面结构.

基于层状弹性体系理论模型,计算不同路面结构的路表弯沉.为了模拟FWD检测有限点弯沉,选取9个计算位置,间隔为30 cm,分布范围为0～240 cm.对于实惰性点法和虚惰性点法,完整弯沉盆信息均基于有限点弯沉通过预测模型预测得到.

3.2.2 土基模量反演误差分析

分别使用实惰性点法和虚惰性点法反演土基模量,土基模量反演值与真值对比见图2.由图可知,实惰性点法和虚惰性点法的模量反演值靠近等值线,表明模量反演精度很高.采用实惰性点法和虚惰性点法计算得到的土基反演模量均方根误差分别为3.00和2.89 MPa,表明这2种方法的模量反演精度均较高,相比而言,虚惰性点法的精度更高.

(a) 实惰性点法

(b) 虚惰性点法

这2种方法的土基模量反演误差绝对值的频率分布见图3.由图可知,实惰性点法和虚惰性点法的土基模量反演误差直方图均偏左,土基模量反演误差小于2%的模拟路面结构数占总模拟路面结构数的比例分别为70.4%和69.5%,反演误差大于5%的模拟路面结构数占总模拟路面结构数的比例分别为1.8%和0.1%.实惰性点法和虚惰性点法的土基模量的平均理论反演误差分别为1.70%和1.53%.这表明虚惰性点法的模量反演精度高于实惰性点法,且误差分布范围更小.

(a) 实惰性点法

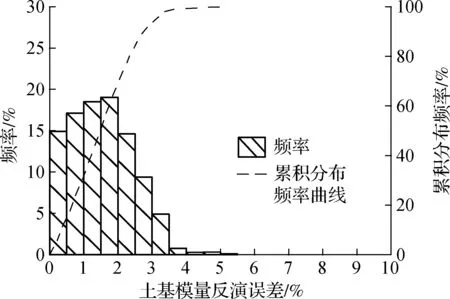
(b) 虚惰性点法

3.2.3 惰性点位置对反演误差的影响

当惰性点位置超出弯沉检测范围时,需要对弯沉盆进行外延,因此惰性点位置对土基模量反演误差有较大影响.表5给出土基模量反演误差按照惰性点位置进行分组统计分析结果,其中惰性点位置的分组间隔为30 cm.由表可知,当惰性点位置在弯沉检测范围内(Rc<240 cm)时,实惰性点法和虚惰性点法的反演误差相近,平均误差分别为1.53%和1.55%;当惰性点位置在弯沉检测范围外(Rc≥240 cm)时,2种方法的反演误差均随惰性点位置外移而增大,但是虚惰性点法的反演误差变化较小,而实惰性点法的反演误差急剧增大,实惰性点法和虚惰性点法的平均反演误差分别为2.63%和1.45%.

表5 不同惰性点位置下的土基模量反演误差 %

当惰性点位置超出弯沉检测范围时,虚惰性点法的反演精度显著优于实惰性点法.这主要是因为实惰性点法和虚惰性点法所用惰性点参数不同,前者计算惰性点参数时所用弯沉盆均由理论推导生成,而后者是通过有限点弯沉预测得到完整弯沉盆信息的.因此,当惰性点位置超出弯沉检测范围时,虚惰性点法的土基模量反演误差更小.

综上所述,当惰性点位置位于弯沉检测范围内时,实惰性点法和虚惰性点法均可用于土基模量反演;当惰性点位置超出弯沉检测范围时,应当使用虚惰性点法进行土基模量反演.

4 实例分析验证

4.1 实测弯沉盆数据和路面结构信息

本文在北方某环道实验路采集了沥青路面弯沉盆数据,该环道实验路铺设了不同类型的路面结构,弯沉盆数据见表6,路面厚度信息见表7.各结构的土基类型相同.对土基表面进行了水泥稳定处治,处治深度为20 cm,水泥用量为9.5%.

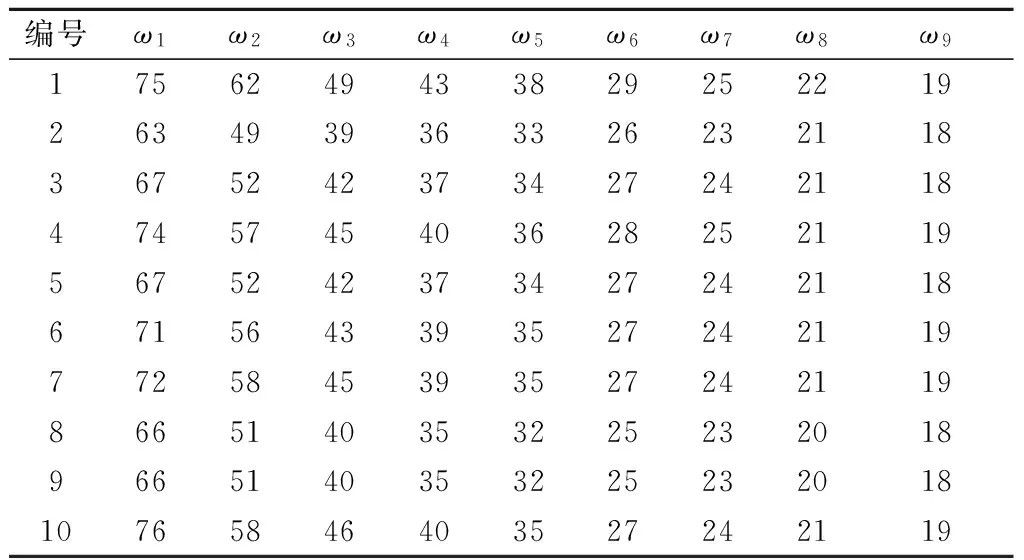
表6 实测弯沉盆 μm

注:ω1,ω2,ω3,ω4,ω5,ω6,ω7,ω8,ω9分别为距离荷载中心点0,30,60,90,120,150,180,210,240cm处的弯沉.

4.2 土基模量反演结果

分别采用虚惰性点法和实惰性点法进行土基模量反演,结果见表7.由表可知,虚惰性点法和实惰性点法的土基模量平均值均为226 MPa,变异系数分别为4.0%和4.2%,二者的反演结果较为一致,这主要是因为惰性点位置均小于240 cm,位于弯沉盆检测范围内.

表7 基于实测弯沉盆的土基模量反演结果

注:ha和hb分别为面层和基层厚度.

4.3 土基模量反演偏差分析

为了分析惰性点位置(Rc)和弯沉检测范围(Ld)对土基模量反演值的影响,分别使用不同检测范围(Ld=150,180,210,240 cm)内的实测弯沉预测完整弯沉盆信息,反演土基模量,并以Ld=240 cm时的土基反演模量为基准,分别计算各反演方法的土基反演模量相对偏差,结果见图4.

图4 弯沉检测范围对土基模量反演值的影响

由图4可知,当惰性点位置较远时,采用2种方法得到的土基模量反演偏差均较大.与实惰性点法相比,当惰性点位置较远时,虚惰性点法的土基模量反演偏差较小;而当惰性点位置较近时,2种方法的反演偏差相近,这与理论模拟分析结果一致.

5 结论

1) 对于FWD检测范围外的弯沉盆信息,指数模型的预测精度较高,且模型所需参数较少,仅2个.对于FWD检测范围内的弯沉盆信息,对数分段线性插值法的预测精度较高,且计算简便.

2) 虚惰性点法和实惰性点法的平均理论反演误差分别为1.53%和1.70%,均具有很高的反演精度.惰性点位置对反演误差有较大影响,当惰性点位置超出弯沉盆检测范围时,虚惰性点法和实惰性点法的平均反演误差分别为1.45%和2.63%.

3) 对于土基相同但路面厚度不同的实测路表弯沉盆,虚惰性点法和实惰性点法的土基反演模量的变异系数分别为4.0%和4.2%.惰性点位置对土基模量反演偏差影响较大.当惰性点位置较远时,与实惰性点法相比,其反演偏差较小,这与理论模拟分析结果一致.

4) 从土基模量反演精度出发,对于弯沉检测范围较小且惰性点位置较远的结构,建议采用虚惰性点法进行土基模量反演.

)

[1] 朱洁. 沥青路面多层结构模量高精度反算方法研究[D]. 上海:同济大学交通运输工程学院, 2013.

[2] Burak Goktepe A, Agar E, Hilmi Lav A. Advances in backcalculating the mechanical properties of flexible pavements[J].AdvancesinEngineeringSoftware, 2006,37(7): 421-431. DOI:10.1016/j.advengsoft.2005.10.001.

[3] 孙立军, 八谷好高, 姚祖康. 水泥混凝土路面板模量反算的一种新方法——惰性弯沉法[J]. 土木工程学报, 2000, 33(1): 83-87,99. DOI:10.3321/j.issn:1000-131X.2000.01.016.

Sun Lijun, Yoshitaka Hachiya, Yao Zukang. A new method to backcalculate layer moduli for concrete pavements[J].ChinaCivilEngineeringJournal, 2000,33(1): 83-87,99. DOI:10.3321/j.issn:1000-131X.2000.01.016.(in Chinese)

[4] Zhang X, Sun L. Novel method for backcalculation of asphalt pavement moduli [J].TransportationResearchRecord:JournaloftheTransportationResearchBoard, 2004,1869: 67-72. DOI:10.3141/1869-08.

[5] 朱洁, 陈长, 孙立军. 沥青路面惰性弯沉点的选取及土基模量的反演[J]. 同济大学学报(自然科学版), 2013, 41(12): 1824-1829. DOI:10.3969/j.issn.0253-374x.2013.12.010.

Zhu Jie, Chen Zhang, Sun Lijun. Selection of inertial point for asphalt pavement and backcalculation method of subgrade modulus[J].JournalofTongjiUniversity(NaturalScience), 2013,41(12): 1824-1829. DOI:10.3969/j.issn.0253-374x.2013.12.010.(in Chinese)

[6] 王旭东, 郭大进, 邓学钧. 动态弯沉盆几何特性分析[J]. 东南大学学报(自然科学版), 1999, 29(5): 115-120. doi:10.3969/j.issn.1001-0505.1999.05.024.

Wang Xudong, Guo Dajin, Deng Xujun. Geometric characteristic analyze of the dynamic deflection basin[J].JournalofSoutheastUniversity(NaturalScienceEdition), 1999,29(5): 115-120. doi:10.3969/j.issn.1001-0505.1999.05.024. (in Chinese)

[7] 刘军忠, 翁兴中, 张俊，等. 应急机场土质道面疲劳变形特性模型试验[J]. 西南交通大学学报, 2014, 49(3): 412-418. DOI:10.3969/j.issn.0258-2724.2014.03.007.

Liu Junzhong, Weng Xingzhong, Zhang Jun, et al. Model experiment of fatigue deformation characteristic of emergency soil airfield pavement[J].JournalofSouthwestJiaotongUniversity, 2014,49(3): 412-418. DOI:10.3969/j.issn.0258-2724.2014.03.007.(in Chinese)

[8] 余欢. 沥青路面半刚性基层损坏评价及刚性下卧层深度设置[D]. 上海:同济大学交通运输工程学院,2015.

[9] Uzan J, Lytton R L, Germann F P. General procedure for back-calculating layer moduli [C]//FirstInternationalSymposiumonNondestructiveTestingofPavementsandBackcalculationofModuli. Baltimore, USA, 1989: 217-228. DOI:10.1520/stp19809s.

[10] 余欢, 陈长. 沥青路面模量反演分析中刚性下卧层设置方法[J]. 交通科学与工程, 2014, 30(4): 1-6. DOI:10.3969/j.issn.1674-599X.2014.04.001.

Yu Huan, Chen Zhang. Setting method of rigid substratum in modulus back-calculation of the asphalt pavement[J].JournalofTransportScienceandEngineering, 2014,30(4): 1-6. DOI:10.3969/j.issn.1674-599X.2014.04.001.(in Chinese)

Back-calculatingmethodforsubgrademodulusbasedonvirtualinertialpoints

Zang Guoshuai Sun Lijun Chen Zhang

(Key Laboratory of Road and Traffic Engineering of Ministry of Education, Tongji University, Shanghai 201804, China)

To improve the back-calculating accuracy of subgrade modulus based on inertial points, the prediction method for the complete deflection basin based on a finite number of deflections was studied. The calculation method for virtual inertial points based on the predicted complete deflection basin curve was proposed. The results were compared with the back-calculated results for the realistic inertial points based on the realistic complete deflection basin curve. The theoretical analysis and the example verification for the back-calculating precision were carried out. The results show that, when the deflections within and outside the detection range are predicted by the logarithmic piecewise linear interpolation method and the exponential fitting model respectively, the prediction accuracy is high and the calculation is convenient. The average theory back-calculating errors for the realistic and virtual inertial point methods are 1.70% and 1.53%, respectively. The position of the inertial point has a great influence on the back-calculating error. When the inertial point is outside the detection range, the average back-calculating errors for the realistic and virtual inertial point methods are 2.63% and 1.45%, respectively. The results based on the measured deflection basin curves are in agreement with the simulation results. Through the improvement of the calculation of inertial point parameters, the virtual inertial point method significantly improves the back-calculation precision of the subgrade modulus.

asphalt pavement; inertial point; deflection basin curve; falling weight deflectometer; modulus back-calculation

10.3969/j.issn.1001-0505.2017.06.023

U416.2

A

1001-0505(2017)06-1227-06

2017-04-29.

臧国帅(1992—),男,博士生;孙立军(联系人),男,博士,教授，博士生导师，ljsun@tongji.edu.cn.

国家自然科学基金资助项目(51678443，71471134)、交通运输建设科技资助项目(2015318822170).

臧国帅,孙立军，陈长.基于虚拟惰性点的土基模量反演方法[J].东南大学学报(自然科学版),2017,47(6):1227-1232.

10.3969/j.issn.1001-0505.2017.06.023.