基于小波神经网络的短时交通流量预测

赵道利，谷伟豪，冯亚平

(西安理工大学 水利水电学院，陕西 西安 710048)

基于小波神经网络的短时交通流量预测

赵道利，谷伟豪，冯亚平

(西安理工大学 水利水电学院，陕西 西安 710048)

短时交通流量预测对于改善交通拥堵、减少环境污染具有重大的现实意义。传统神经网络进行短时交通流量预测难度大，精度低。为了提高预测精度，采用一种小波神经网络模型，小波神经网络具有小波分析和神经网络两者的优点，非线性拟合能力强，收敛速度快，训练精度高，可以对短时交通流量预测进行局部分析，非常适合非线性预测。文中建立了小波神经网络模型，构造了交通流量样本集，对样本数据训练至收敛，然后选取一定数量的样本数据进行测试。测试结果表明，采用小波神经网络进行短时交通流量的预测不仅预测精度高，而且收敛速度快，实时性好，具有一定的应用价值。

短时交通流量；小波分析；神经网络

0 引言

随着我国城市化进程的大力发展，机动车数量剧增，导致城市道路拥堵、交通事故以及环境污染等一系列的问题。因此，城市交通问题已是困扰着民生的大问题。为了有效控制和管理城市交通，有必要对交通流量进行实时准确的预测，然后交通部门可以采取有效的控制策略来对交通流量进行疏导和控制，保障机动车的畅通无阻，改善交通拥堵状况。

目前短时交通预测方法主要有两类：一类是时间序列预测，例如参数回归模型预测、卡尔曼滤波模型等，这类预测方法原理简单，考虑的影响因素少，因此预测精度不高，无法考虑突发性因素的影响；另外一类是非线性预测模型，例如神经网络、支持向量机、小波神经网络等方法，这类模型的非线性逼近能力好，而短时交通流量具有高度复杂性、不确定性，非线性预测模型可根据这个特点进行建模预测。

文献[1]根据道路交通流量的复杂性和不确定性，提出一种改进K近邻非参数回归预测算法，取得了良好的预测结果。文献[2]提出改进的BP神经网络模型，与传统的BP神经网络预测相比，精度更高。文献[3]采用小波支持向量机进行预测，先将交通流量进行小波分解，得到高频部分和低频部分，再分别利用支持向量机进行预测。文献[4]针对RBF神经网络预测中收敛速度慢和泛化能力差等问题，提出将粒子群算法应用到RBF神经网络中，进行参数优化。文献[5]针对时间序列模型的缺陷提出改进时间序列模型的预测方法。文献[6]将小波分析与神经网络相结合，用来进行短时交通流预测。文献[7]将多种模型预测结果综合起来，利用贝叶斯网络进行学习，选定学习概率最大的为最终的预测结果。

本文主要研究了城市短时交通流量的预测方法。根据交通流量的不确定性和复杂性，通过分析影响交通流量的因素从而得出短时交通流量预测的可行性。选取某个城市某个交叉路口的交通流量作为数据来源，利用小波神经网络进行短时交通流量的预测，目的是提高训练的收敛速度以及预测的精度。仿真验证了该方法在交通流量预测中的效果。

1 短时交通流量分析

城市交通系统是一个时变的、不确定的系统，交通流量随着时间的变化而变化，但每个市民的出行要受到城市交通状况的制约，并且每个市民的出行具有一定的规律，因此交通流量在一定程度下还是有规律可循的。交通流量的特性分析主要有以下几个方面：

(1)不确定性

交通流量的不确定性因素很多。例如，车辆的类型和性能不同；机动车司机的驾驶水平参差不齐，心理素质也不相同，对突发情况的反应时间不同；天气因素的影响等。影响交通流量的因素很多，所以交通流量的不确定性很大，预测的时间越短，不确定性因素也就越多。

(2)周期性

交通流量在时间周期内呈现一定的周期性。据交通部门统计，在同样的路段同样的时间段内交通流量虽然有一定的波动，但是从整个周期来看，以一周为例，是呈现周期性变化的。交通流量是随着交通需求的变化而变化的，而社会中人们的出行规律、出行需求表现出一定的规律性，所以交通流量也呈现周期性的规律。交通流量呈现周期性的变化也为交通流量的预测提供了一定的技术支持。

综上所述，交通流量呈现高度的不确定性但是又存在一定的周期性，不确定性为交通流量的预测增加了困难，周期性又为交通流量的预测增加了可行性。

表1列举了常用的短时交通流量预测方法。如表1所示，现有的交通流量预测方法很多，有的方法只能用于预测线性的交通流量，有的方法模型太过复杂，有的方法可用于预测复杂多变的交通流量，其中，小波神经网络具

表1 常见的短时交通流量预测方法对比

有预测精度高、收敛速度快的特点，同时它可用于预测非线性的交通流量，因此，本文选取小波神经网络来预测交通流量。

2 短时交通流量预测模型

短时交通流量预测模型的建立原则如下:

(1)精确性：交通流量的预测结果只有满足精度要求，才能获得实际应用，如果预测结果精度不高，也就没有了研究意义。

(2)实时性：交通流量预测要求必须在规定的时间内得到计算结果，才能及时获得交通预测结果，进而进行必要的交通协调控制。因此，实时性是很重要的。

(3)动态反馈性：交通流量预测不仅要实时准确地进行预测，而且还要动态反馈，当交通流发生异常时，要根据实际情况反馈到预测模型，从而进行相应的调整，确保实时更新。

2.1 小波分析

小波分析在时域和频域都有良好的局部特性，与传统傅里叶变换不同，小波分析可通过平移母小波获得良好的时间特性，通过缩放小波的尺度获得良好的频率特性。

假设x(t)是平方可积函数[x(t)∈L2(R)],ψ(t)为母小波的函数，则称：

(1)

为x(t)的连续小波变换。其中，(*)代表共轭；a是尺度因子(a>0)；τ是位移，可正可负。尺度a的作用是将小波ψ(t)作伸缩，a越大，ψ(t/a)越宽。

小波变换的逆变换如下：

(2)

小波函数有很多种。不同的小波函数其变换后的效率和结果也不同。目前常用的小波函数有Haar小波、Morlet小波、Mexican hat小波等。

2.2 小波神经网络

小波神经网络是将小波和神经网络结合，将神经网络中的传递函数用小波函数替代，综合了小波分析良好的时频分析能力和神经网络强大的自学习能力，因此小波神经网络拥有非常强大的非线性拟合能力和模式识别能力。

小波神经网络结构图如图1所示。

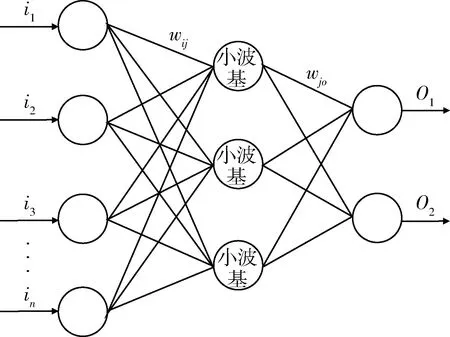
图1 小波神经网络结构

图1中，i1,i2,i3,…,in是小波神经网络的输入，o1,o2是小波神经网络的输出，ωij是从输入层到隐含层的权值，ωjo是从隐含层到输出层的权值，隐含层的输出为：

(3)

式中，Sj为隐含层中第j个节点的输出，f(j)为小波基函数，bj为小波基函数的平移参数，aj为小波基函数的伸缩参数。

本文选取Morlet为小波基函数，其数学表达式如下：

(4)

Morlet小波基函数的时域和频域图像如图2所示。

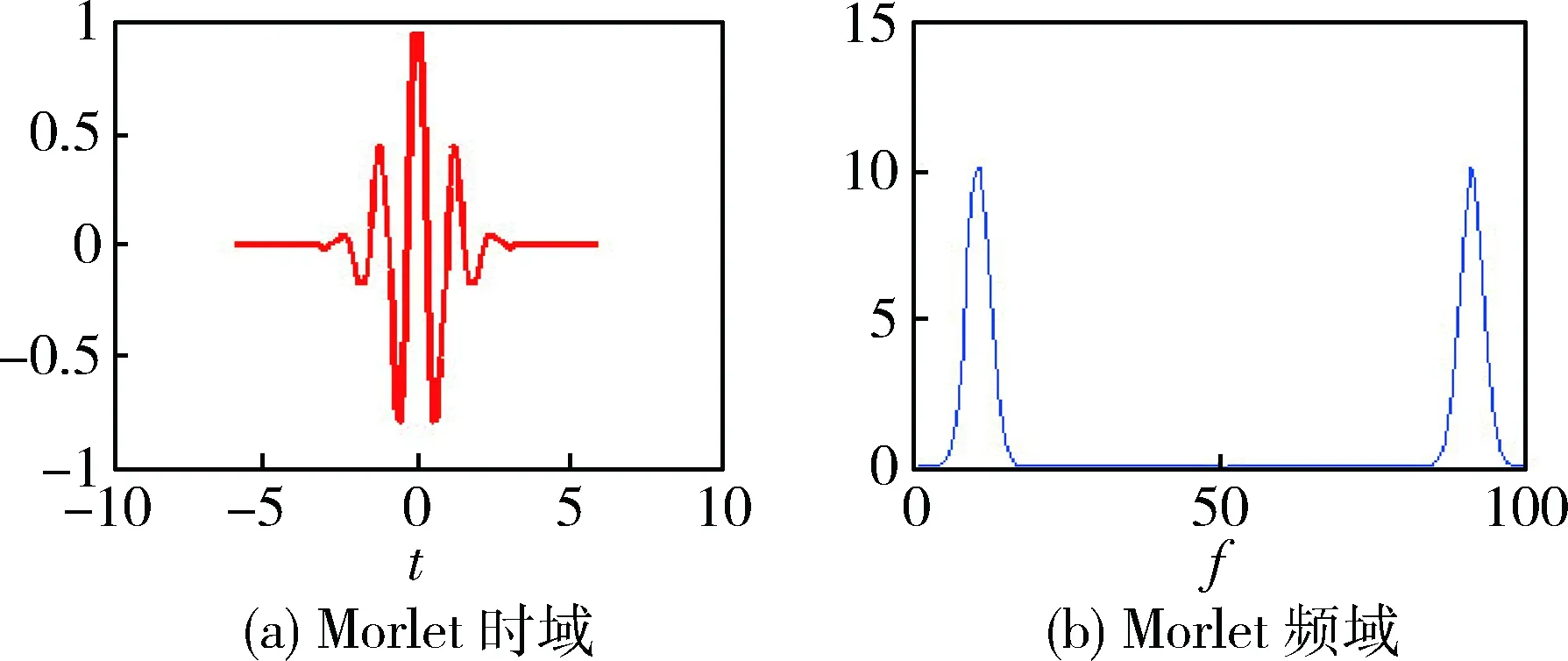
图2 Morlet小波基函数时频域图像

小波神经网络输出层输出为：

(5)

式中，ωjo为从隐含层到输出层的权值，S(j)为隐含层中第j个节点的输出，l为隐含层节点个数，m为输出层节点个数。

小波神经网络的权值修正是利用梯度下降法对小波基函数和网络的权值进行修正优化，不断接近网络的期望输出。修正过程如下：

(1)计算误差

(6)

式中，yn(k)为网络的期望输出，y(k)为网络的实际输出。

(2)误差E修正

(7)

(8)

(9)

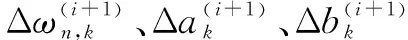
(10)

(11)

(12)

式中，η为网络学习效率。

2.3 小波神经网络预测流程

小波神经网络训练流程如图3所示。

3 仿真与结果分析

3.1 短时交通流量样本的预处理

在短时交通流量预测中，从道路两侧和交叉路口的交通流量采集装置等智能装置上采集到的交通流量样本数据数量众多且大小单位不一致，因此需对样本集进行归一化处理。

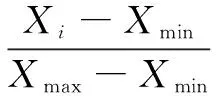
(13)

式中，X为归一化后的样本值，Xi为归一化前的样本值，Xmax和Xmin分别为每组样本中的最大值和最小值。

3.2 小波神经网络的构造

小波神经网络的构造是根据短时交通流量的特性来设计的。根据短时交通流量的特点，选定小波神经网络为三层：输入层、隐含层和输出层。输入层的输入为当前时间点的前4个时间点的交通流量，每个时间点共采集276点的流量数据，因此，小波神经网络的输入节点为4个。各个时间点的交通流量原始数据图如图4所示。

隐含层节点是由Morlet小波函数构成的，隐含层层数选用单隐层结构。对于隐含层节点数目，迄今尚未有明确

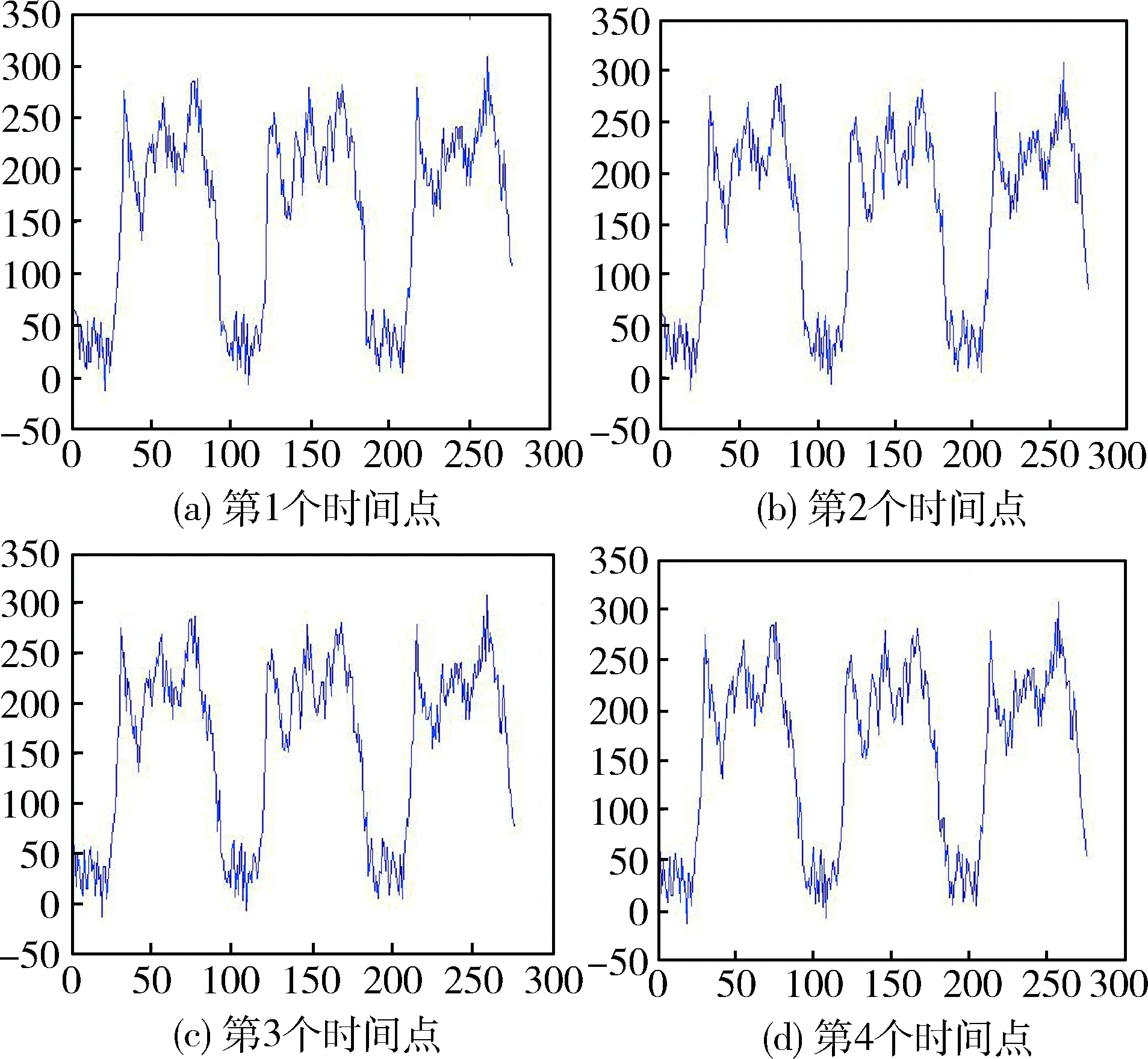
图4 原始数据图

的公式，隐层节点数目的确定根据试凑法确定，参照如下公式设计：

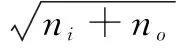
(14)

式中，n为隐含层节点数，ni为输入层节点数，no为输出层节点数，a范围为1～10。

根据式(14)可确定隐含层节点数在3～12之间。具体数目还需根据网络的训练次数和误差来确定。先选择较小的隐含层节点数，然后在样本数不变的情况下逐步增加隐含层节点数目，以此种方法来训练神经网络，选择在误差最小情况下的隐含层节点数为最终结果。小波神经网路的学习采用有导师学习，传输函数选择Morlet小波函数，训练算法采用梯度下降法。对神经网络进行训练的目的就是使误差函数E值最小，本文设置网络的训练误差为0.001，最大迭代次数为500次。

3.3 小波神经网络的预测结果

将上述样本数据经过归一化处理后，作为小波神经网络模型的输入。向网络中输入样本集后，开始训练小波神经网络。首先选择较小的隐含层节点数3，然后逐渐增加到12。观察网络模型的误差曲线，最终得出当隐含层节点数为6时误差最小。因此，选定隐含层节点数为6，此时小波神经网络训练曲线如图5所示。图5中，小波神经网络在第415次时误差达到0.001，保存网络，然后对网络进行测试，预测结果如图6所示。

图6中，除个别时间点以外，在整个趋势上小波神经网络的预测精度很高。

图5 训练曲线图

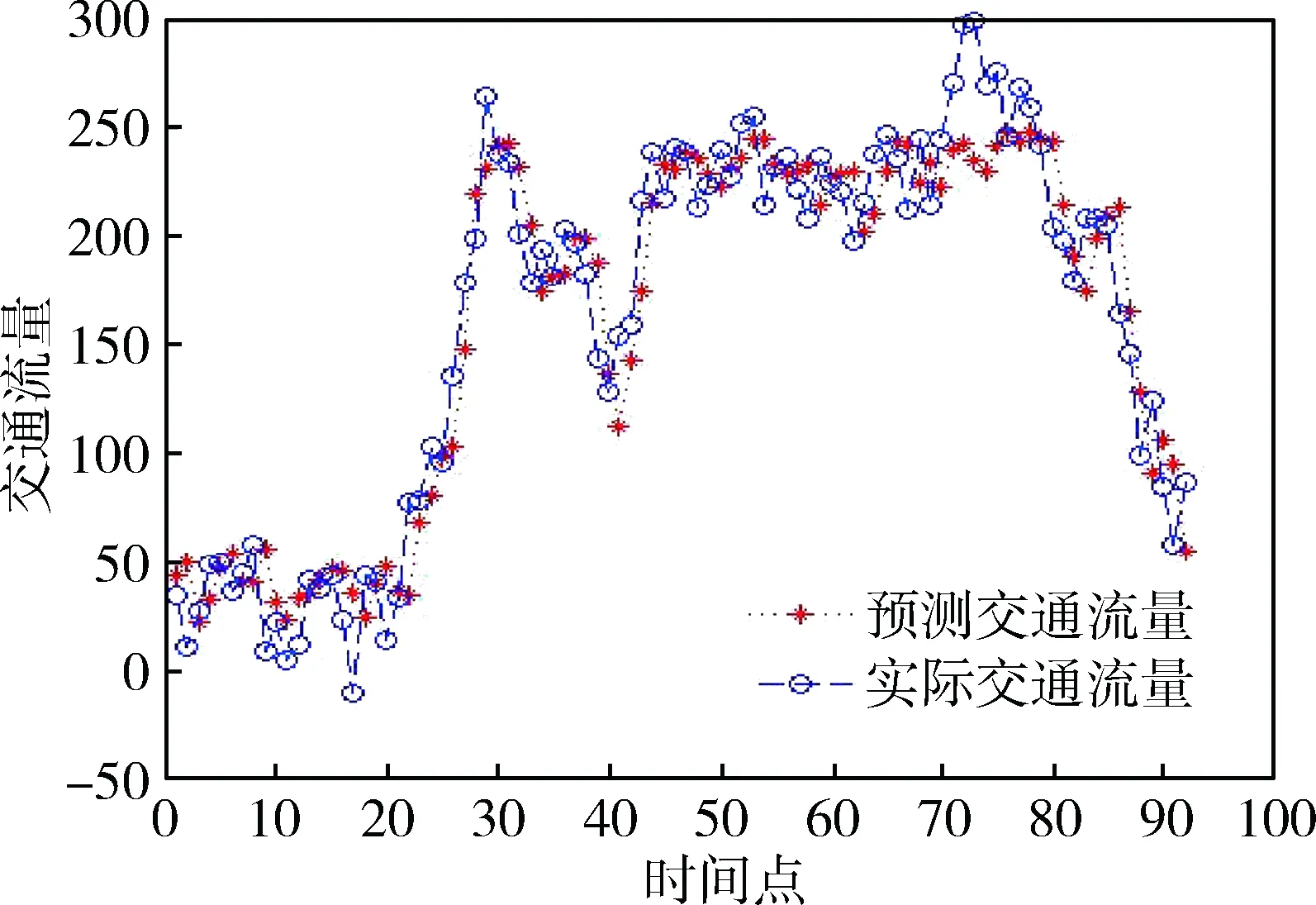
图6 小波神经网络短时交通流量预测图

3.4 预测性能分析

为了进一步评价小波神经网络的预测结果，本文选用了两种性能评价指标：均方误差(MSE)和平均绝对误差(MAE)，分别计算了BP神经网络和小波神经网络的均方误差和平均绝对误差，计算结果如表2所示。

由表2可知，小波神经网络模型的均方误差(MSE)为97.96，平均绝对误差(MAE)为5.679 3，这两个值与BP神经网络相比都小得多，说明小波神经网络的收敛速度很快，而且网络的预测精度很高。

表2 预测性能分析

4 结束语

短时交通流量具有高度的时变性、复杂性、不确定性，其预测难度比中期和长期交通流量预测难度要大。本文利用小波神经网络对其进行预测，预测结果表明小波神经网络可以很好地进行短时交通预测，并且精度很高，具有一定的应用价值。

[1] 范鲁明. 基于非参数回归的短时交通流量预测[D].天津:天津大学,2012.

[2] 张佳宁. 基于神经网络的城市交通流量预测模型研究[D].广州：广东工业大学,2016.

[3] 崔艳,程跃华. 小波支持向量机在交通流量预测中的应用[J].计算机仿真,2011,28(7):353-356.

[4] 冯明发,卢锦川. 粒子群优化RBF神经网络的短时交通流量预测[J].计算机仿真,2010,27(12):323-326.

[5] 唐毅,刘卫宁,孙棣华,等. 改进时间序列模型在高速公路短时交通流量预测中的应用[J]. 计算机应用研究,2015,32(1):146-149.

[6] 王芬,马涛. 基于小波神经网络的短时交通流预测[J].宁夏师范学院学报,2012,33(6):60-62.

[7] 王建,邓卫,赵金宝. 基于贝叶斯网络多方法组合的短时交通流量预测[J].交通运输系统工程与信息,2011,11(4):147-153.

Short time traffic flow prediction based on wavelet neural network

Zhao Daoli, Gu Weihao, Feng Yaping

(College of Water Resources and Electric Power, Xi’an University of Technology, Xi’an 710048, China)

Short time traffic flow forecasting is of great significance for improving traffic congestion and reducing environmental pollution.Traditional neural network is very difficult to predict short time traffic flow and has low precision.In order to improve the prediction accuracy, a wavelet neural network model is adopted. Wavelet neural network has the advantages of both wavelet analysis and neural network, with strong nonlinear fitting ability, fast convergence speed and high precision of training,which is very suitable for nonlinear prediction. So partial analysis of short-term traffic flow forecasting can be carried out. The wavelet neural network model is established in this paper, a traffic flow sample set is constructed. The sample data is trained to convergence, and then a certain number of sample data are selected for testing. The test results show that the wavelet neural network for short time traffic flow prediction not only has high prediction accuracy, but also the convergence speed is fast, the real-time performance is very good, and has certain application value.

short time traffic flow; wavelet analysis; neural network

TP391； P208

A

10.19358/j.issn.1674- 7720.2017.23.023

赵道利，谷伟豪，冯亚平.基于小波神经网络的短时交通流量预测[J].微型机与应用，2017,36(23)：80-83.

2017-06-09)

赵道利(1973-)，男，在职博士，副教授，主要研究方向：故障诊断。

谷伟豪(1990-)，通信作者，女，硕士研究生，主要研究方向：人工智能算法的应用。E-mail：nerilian@163.com。

冯亚平(1990-)，男，硕士研究生，主要研究方向：故障诊断。