一种新型粒子群改进遗传算法

刘 露，陈 赞，刘世劼，章 静，朱雯雯

(1.上海航天控制技术研究所，上海 201109； 2.上海航天电子通讯设备研究所，上海 201109； 3.上海航天技术研究院，上海 201109)

一种新型粒子群改进遗传算法

刘 露1，陈 赞2，刘世劼2，章 静3，朱雯雯1

(1.上海航天控制技术研究所，上海 201109； 2.上海航天电子通讯设备研究所，上海 201109； 3.上海航天技术研究院，上海 201109)

传统优化算法均存在各种局限，无法同时满足性能优良算法的几个标准：不容易陷入局部最优解、收敛速度较快、具有框架性及可结合性。在传统粒子群与遗传算法的基础上，结合其他常用算法，提出一种新型混合智能优化算法——粒子群改进遗传算法。该算法在变异环节、交叉环节、淘汰环节中引入许多其他算法的优点加以改进。最后，通过修正某控制系统的控制参数验证了新算法相对于传统单一优化算法的先进性。

遗传算法；粒子群算法；模拟退火；局部最优

0 引言

借鉴于生物生态学的物种进化理论，基于种群的智能优化算法以其独有的并行搜索优势吸引了众多科研工作者的研究。其概念首次提出于1966年，由Fogel等人提出了进化规划，由Rechenberg和Schwefel提出了进化策略。在此基础上，作为智能算法领域最经典的遗传算法于1975年由Holland[1]提出，并于1992年由Koza通过其提出的遗传规划加以完善。

经过50多年的发展，一个性能良好的种群智能优化算法应该具有全局随机搜索规律、全局优化性能、鲁棒性、高搜索精度和收敛速度快等优点。

现阶段比较常用的智能算法如遗传算法、粒子群算法、蚁群算法、模拟退火算法等均存在各种局限，无法同时满足性能优良算法的5个标准，例如遗传算法易过早收敛、粒子群算法搜索精度不高、蚁群算法易陷入局部最优解且收敛速度慢[2]。

若将各个智能算法的优势混合应用，可得到一个同时具有多个算法优点的新算法[3]。本文在遗传算法的基础上引入其他优化算法的局部环节，提出了一种新智能算法——粒子群改进遗传算法。

1 粒子群改进遗传算法概述

粒子群改进遗传算法使用标准遗传算法作为算法的主框架，在变异环节、交叉环节、淘汰环节中引入许多其他算法的优点加以改进。其添加的主要环节及效果概述为：改进基础变异、引入强化变异、改进交配对象选择方法、改进交叉环节、自适应调节迭代速率、改进淘汰机制、改进单一优化目标，以及陷入最优解的自我调整。

该算法综合了近10种算法的优秀特性，主要适用于求解复杂、大型、具有很多局部最优解，对优化的精度要求较高，且优化问题对优化时间的要求并不严苛的优化问题。

2 算法细节设计

2.1 算法变异环节设计

算法变异环节包括粒子群移动变异和变异环梯度变异两个顺序进行的环节，其具体设计如下：

在粒子群移动变异的过程中，首先更新每个粒子群的最优性能及全部粒子群的最优性能。随后，按标准粒子群算法更新全部个体的运动速度，并计算每个个体的速度是否满足速度约束条件，如果超速，则将该个体的对应性能调整为超速的临界点[4]。然后，在上一步得到粒子运动速度的基础上，对全部个体的性能进行更新，并检查更新后的个体性能是否满足约束条件，若不满足则将对应个体性能调整为约束条件的临界点，从而完成粒子群迭代的单步操作。

在变异环节中，父本变异的步骤主要为以下几步：

(1)在全部待优化参数组成的高维空间中随机选择一组向量，作为待变异环的法向方向，选择本步迭代的迭代步长，作为待变异环的半径，选择待变异的父本个体作为变异环的圆心，就此组成变异环；

(2)在变异环中平均选取10个点作为子代胚胎，并求出各个胚胎的适应度指标，对全部子代胚胎连同其父本进行性能排序，选取前2名作为该父本变异后得到的子代个体；

(3)子代个体在粒子群环节的相关属性如粒子最优性能和运行速度均与其父本相同。

2.2 算法交叉环节设计

算法的交叉环节包含选择交配对象、生成子代胚胎及子代和引入移民个体等三个顺序执行的步骤，其设计流程图如图1所示。

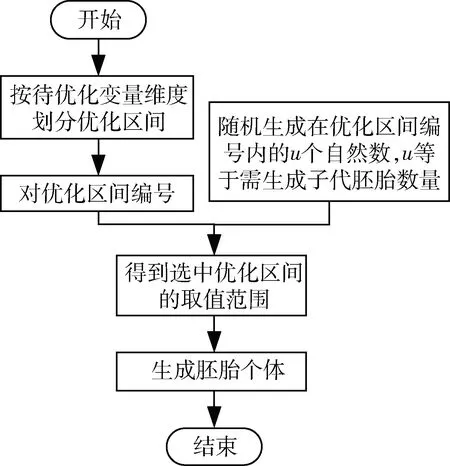
图1 生成胚胎的算法设计流程图

生成胚胎后对全部胚胎及其父母进行性能排序，选取前2名作为该父母的子代。交叉环节的第三步为添加移民算子。移民算子的实现比较简单，在算法优化空间中随机初始化Nadd数量的粒子，计算这些粒子的适应度函数，并将满足基本约束条件的粒子加入到种群中。

2.3 算法淘汰环节设计

经过遗传、交叉两个大环节的演算，粒子总数量已达到该步迭代前的4～6倍，因此，需要淘汰环节保持种群数量的一致性[5]。取种群平均马氏的一半作为种群间个体距离过近评判标准的阈值MTS，对种群中个体间距离小于阈值的个体对进行内部淘汰，即对这两个距离过近的个体按性能指标排序，将排序末位个体淘汰。

2.4 算法的自适应性

2.4.1迭代收敛程度的量化

收敛程度的量化可分为三个部分：最优个体适应度值的进步程度Ebest、平均适应度值的进步程度Eava及个体间的集群聚集程度Ddr。各个指标的计算方法如式(1)～式(3)所示：

Ebest,i=100×

(1)

(2)

(3)

其中，Fj,i表示第i次迭代，种群第j个个体的适应度指标。系统的综合迭代收敛程度指标Ecm写作如式(4)所示：

Ecm=Kava×Eava+Kbest×Ebest+Kdr×Ddr

(4)

式(4)中各个指标的系数由各个指标的物理意义、量纲及权重决定。对于描述进化速度百分比Ebest和Eava的两个指标，本文取适应度指标在50代内增加30%为判定收敛的界限，经过计算，Ebest和Eava两个指标判定为收敛的界限为0.53%；而对于描述代内代际性能指标分布比率的指标Ddr，本文取分布比率为1作为判定收敛的界限[6]。取这三个指标的权重分别为30%、30%和40%，得到综合迭代收敛程度的表达式如式(5)所示：

(5)

将式(5)整理，得到其标准计算公式如式(6)所示：

Ecm=0.556×Eava+0.556×Ebest+0.4×Ddr

(6)

因此，当综合收敛指标Ecm小于1时，可判定该步迭代系统处于收敛的状态。

2.4.2基于算法收敛程度的调整

该算法的核心在于迭代过程中根据收敛的程度动态调整迭代控制参数。当种群趋向于收敛时，需要动态调整迭代控制参数来保证算法的搜索范围、迭代精度等。算法中可自适应修正的变量及其性质如表1所示。

表1 优化算法可修正变量一览表

当综合收敛指标小于1时，即将4个自适应变量向收敛趋势方向调整，反之则向相反的方向调整，其调整幅度与综合收敛指标的数值有关。该算法可使整体迭代过程更具有智能性。

3 控制器设计的实物验证

本文分别用普通遗传算法、普通粒子群算法、改进遗传算法及粒子群改进遗传算法4种方法解决实际工程问题，以此验证提出的新算法相对传统优化算法的先进性。

3.1 优化问题及优化指标

该优化问题为修正某控制系统的控制参数，以使该控制系统对阶跃信号产生的输出信号的震动及内部电机输入信号的震动最小化。待修正的原控制系统结构图如图2 所示。

图2 原控制结构结构图

由于震荡会导致系统运行故障，降低系统运行可靠性，因此，需要通过修改系统参数或系统结构来消除或最大程度地减弱震荡。首先对系统的输出震荡程度进行数学描述，其震荡程度Evib的评价指标的计算公式如式(7)所示：

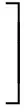
(7)

其中，e1(t)、e2(t)分别为电机输入信号和系统输出信号，S1、S2分别为电机输入信号和系统输入信号在tn时间内的震动次数。

3.2 4种优化算法求解效果对比

调节控制系统参数使系统的震荡程度Evib最小化，需要调节的控制参数k1～k8如图3所示。

图3 系统可调节参数图

使用普通遗传算法、粒子群改进遗传算法、普通粒子群算法及其他文献中的抽象粒子群遗传算法分别对系统可调节系数进行100代优化迭代，得到经过4种算法迭代优化后的可调节参数组合，4种优化参数下系统的输出信号和电机的输入信号分别如图4和图5所示。

图4 4种优化算法100次迭代后输出信号图

由图4～图5可以看出，4种优化算法经过100代优化迭代得到的系统输出信号及电机输入信号的震动均在1.3 s后达到平稳，而粒子群改进遗传算法相较于其他3种算法其输出信号和电机输入信号均震动程度更小，波动更加平稳。因此，可验证粒子群改进遗传算法是一个优化性能更好的算法。

图5 4种优化算法100次迭代后电机输入信号图

4 结论

本文在传统粒子群与遗传算法的基础上，结合其他常用算法，提出一种新型智能优化算法——粒子群改进遗传算法。该算法在变异环节、交叉环节、淘汰环节中引入许多其他算法的环节并为了性能优化结果的进一步提高而加以改进。该算法相对于普通遗传算法或普通粒子群算法均具有很强的收敛性能和规避局部最优解的能力，而算法的时间开销依旧在可接受范围内。

[1] 戴朝华.搜寻者优化算法及其应用研究[D]. 成都：西南交通大学，2010.

[2] 匡芳君.智能混合优化算法及其应用研究[D]. 南京：南京理工大学，2014.

[3] 关沫, 佟彤. 多核系统的实时任务调度算法研究[J]. 微型机与应用, 2016, 35(2):17-19.

[4] AVRIEL M.Nonlinear programming:Analysis and methods[M].Mineola, NY: Dover Publishing,2003.

[5] FOGEL L J,OWENS A J,WALSH M J.Artificial inmlligence through simulated evolution[M]. New York: Jollll Wiley,1966.

[6] RECHENBERG I. Evolutions strategie-optimierung technischer systeme nach prinzipien der biologischen evolution[M]. Stuttgart: Fromman-Holzboog,1973.

A new particle swarm optimization improved genetic algorithm

Liu Lu1, Chen Zan2, Liu Shijie2, Zhang Jing3, Zhu Wenwen1

(1. Shanghai Aerospace Control Technology Institute, Shanghai 201109, China;(2. Shanghai Aerospace Electronic Technology Institute, Shanghai 201109, China;3. Shanghai Academy of Spaceflight Technology, Shanghai 201109, China)

There are several limitations in the traditional optimization algorithms, which can not satisfy the performances of excellent algorithms at the same time: it is not easy to fall into the local optimal solution, the convergence speed is faster, have a framework and compatibility. In this paper, based on the traditional particle swarm and genetic algorithm, combined with other commonly used algorithms, a new intelligent optimization algorithm is proposed which is called Particle Swarm Optimization Improved Genetic Algorithm. The algorithm introduces many advantages of other algorithms in the process of variation, intersection, elimination and improves the performance of optimization results. Finally, the application in optimizing parameters in a control system proved the advantages of the new algorithm.

genetic algorithm; particle swarm optimization algorithm; simulated annealing algorithm; local optimal

TM46; TN86

A

10.19358/j.issn.1674- 7720.2017.23.005

刘露，陈赞，刘世劼，等.一种新型粒子群改进遗传算法[J].微型机与应用，2017,36(23)：17-20.

2017-06-06)

刘露(1991-)，女，硕士，工程师，主要研究方向：飞行控制系统仿真测试。

陈赞(1982-)，男，硕士，工程师，主要研究方向：通信系统设计。

刘世劼(1987-)，男，硕士，工程师，主要研究方向：通信系统设计。