一种基于双界面函数的界面捕捉方法1)
2017-12-18何志伟骆龙山田保林2
李 康 刘 娜 何志伟 骆龙山 田保林2)
*(北京应用物理与计算数学研究所,北京100088)
†(中物院高性能数值模拟软件中心,北京100088)
一种基于双界面函数的界面捕捉方法1)
李 康*,†刘 娜*,†何志伟*骆龙山*,†田保林*2)
*(北京应用物理与计算数学研究所,北京100088)
†(中物院高性能数值模拟软件中心,北京100088)
基于代数重构思想,发展了一种新的双界面函数重构方法,并采用双正弦函数构造了双正弦界面重构方法(double sine interface capturing,DSINC).为验证不同界面函数对界面捕捉效果的影响,用数值方法求解了可压缩五方程模型,其中对流项的离散采用五阶WENO(weighted essentially non-oscillatory method)格式,时间积分采用三阶Runge--Kutta方法,通量计算分别考虑了HLL和HLLC方法,而状态方程采用Mie-Grneisen状态方程.在数值计算中,在界面附近,采用DSINC来获得体积分数的重构,而在远离界面的区域采用WENO格式来获得高阶插值状态.相比采用单界面函数的方法,如双曲正切界面重构方法(tangent of hyperbola for interface capturing,THINC),DSINC方法同样具有界面重构算法简单,在程序中添加方便等特点,两者区别在于,DSINC方法在重构过程中未知函数更易于求解,而无需求解复杂的非线性超越方程,这就使其具有易于向多维扩展的能力.一些典型的两相流动问题,如圆形水柱对流问题,两相三波点问题和激波--界面不稳定性问题等被用作不同界面函数对界面捕捉效果的影响对比.对比分析发现,DSINC与THINC在界面捕捉效果上大致保持一致,并在计算中表现出了较好的稳定性.双界面函数重构思想可以为多相流动界面的代数重构提供了一种新的思路.
多相流动,界面捕捉,双曲正切界面重构方法,双界面函数重构,双正弦界面重构方法
引言
界面分割不同流体的研究在许多科学和工程领域都有重要的应用价值,如超燃冲压发动机、天体物理Rayleigh-Taylor(RT)不稳定性和惯性约束核聚变等[1].在界面问题的数值模拟过程中,界面的演变问题受到格外的关注.如何更精确捕捉界面特征,降低数值方法带来的界面耗散以及更真实反映流动特征,一直是当前界面研究中重点关注的问题.
从方法类型上来区分,界面捕捉方法有两种,一是界面追踪方法(interface tracking method,IT),另一个是界面捕捉方法(interface capturing method,IC).在界面追踪方法中,界面位置可以显式给出,如阵面追踪方法 (front-tracking method)[2-5]和标记法 (marker method)[6-7].然而,界面追踪方法虽可以有效地标识界面的位置,但在处理大变形界面和拓扑变化界面时存在困难.在界面捕捉方法中,界面位置通过隐式方法给出,如水平集方法(level-set method,LS)[8-9]和流体体积分数方法(volume-of- fl uid method,VOF)[10].LS方法通过引入一个带符号的距离函数来确定界面位置,界面位于函数等于零处,所捕捉的界面十分陡峭,但其不足之处是不满足离散守恒(体积守恒或质量守恒).VOF方法采用体积分数来分辨界面的位置,该方法最大的优点是可以保证体积守恒,但由于耗散性,界面的分辨率不高,即使采用高精度方法也无法完全去除界面耗散[11].Sussman等[12]结合LS和VOF方法的优点,采用耦合的LS-VOF方法研究多相流动界面问题时,界面模拟的可信度明显提高.So等[13]将反扩散 (anti-di ff usion)方法用于多相流的求解,通过引入反扩散项来降低界面的耗散,随后将反扩散方法拓展至可压缩多相流动的数值模拟中[14].这些数值模拟技术的提出在一定程度上能够有效解决界面问题研究中的一些问题.
除上述数值模拟技术外,界面重构技术在界面问题的研究中也占有重要地位.从构造过程来看,界面重构分为代数重构和几何重构.Youngs等[15]提出了分段线性界面重构(piecewise linear interface calculation,PLIC)的方法,采用几何重构方法通过分段的线性函数来重构界面.而近年来,代数重构方法在获得清晰界面方面同样受到了广泛关注.Xiao等[16-17]采用双曲正切函数重构界面,从而使得数值模拟中的界面更为陡峭,由于采用的双曲正切重构(tangent of hyperbola interface capturing,THINC)方法不同于 PLIC几何重构方法[15]的复杂过程,THINC过程简单,在程序中添加方便.从构造思路来看,THINC方法的主要针对一维问题,在处理实际的多维问题时需要采用分裂方法或者多次积分的方法.Li等[18]考虑到采用分裂的方法将一维THINC方法拓展至多维情况可能会降低界面模拟的可信度,将THINC方法通过多次积分的方法拓展至多维情况.针对其中的双曲正切函数多次积分的困难问题,其采用了高斯积分克服了困难.考虑不同的界面函数会对界面捕捉效果产生不同的影响,Cassidy等[19]分别采用分段的直线、正弦函数作为界面函数来构造界面得到分段线性界面方法(piecewise linear interface capturing,PLINC)、分段正弦界面方法(piecewise sine interface capturing,PSINC),结果表明:不同的界面函数(线性或正弦)均可以获得较为陡峭的界面,但针对不同的问题时略有差异.对以上代数界面重构方法的对比发现,这些方法均采用单界面函数来重构界面,因此本文中称之为单界面函数代数重构方法.
对于单界面函数重构方法来说,为了保证单元体内的质量守恒,即使界面重构函数较为简单,在实际构造过程中由于需要对界面函数进行守恒积分,单界面函数在守恒积分时的求解过程也甚为复杂.为了进一步研究界面重构函数对数值模拟结果的差异以及进一步评估多维界面重构时的简易方法,本文提出一种基于双界面函数的重构方法,并采用双界面重构思想构造了双正弦界面重构方法,对比了不同类型界面重构函数对数值结果的影响差别.本文的组织结构如下.第1部分介绍所采用的数值方法.第2部分详细给出双界面重构的思想和双正弦界面函数构造方法.数值计算结果在第3部分给出.第4部分介绍研究结论.
1 数值方法
1.1 控制方程:可压缩多相流五方程模型
对于不可溶、无黏的可压缩两相流动来说,流动过程可用五方程来描述
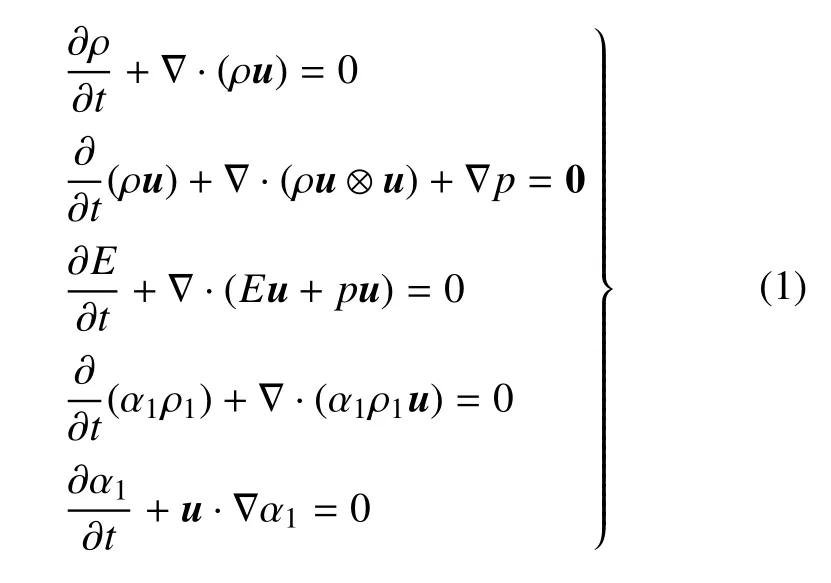
式中,ρ为混合密度,ρi为第i相的密度,u=(u,v)为流动速度,p为压力,E为总能,αi为第i相的体积分数.五方程模型除了包含质量、动量和能量三大守恒方程外,还包括组分质量守恒和体积分数演化方程.界面重构后,通过对流场中的密度和总能做相应的修正,保证在界面处的质量、动量和能量守恒[11].对流项的数值离散采用常用的五阶WENO格式和HLL或HLLC方法求解[20-21].
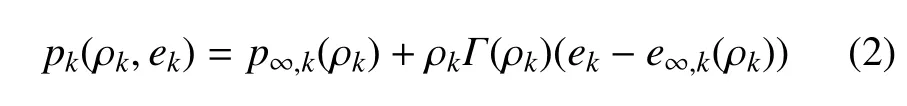
在等压假设下,方程(2)可以导出
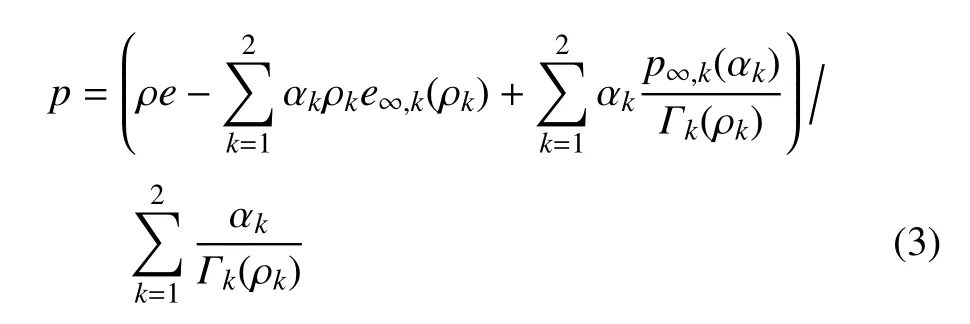
在式 (2)和式 (3)中,ek为分相k的内能,Γk(ρk)=(1/ρk)(∂pk/∂ek)|ρk,p∞,k和e∞,k定义压力和内能的参考状态.
1.2 原始的THINC界面重构方法
以一维情况为例,先介绍THINC的构造思想[16],然后以此为基础,进一步介绍采用双界面函数的界面重构方法的构造思想.设为t时刻单元体i的平均体积分数,αi(x,t)为t时刻体积分数在单元体i中的分布.因此,对于单元体i来说,即x∈ [xi−1/2,xi+1/2],有
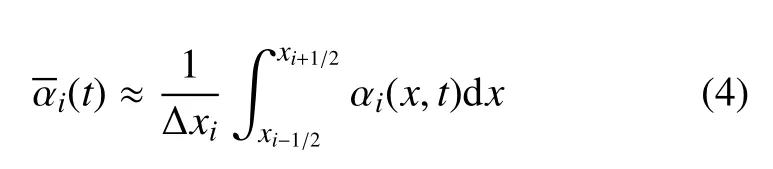
式中,∆xi=xi+1/2−xi−1/2为单元体的网格尺寸.根据体积分数的定义,有

在实际计算中,需要定义界面单元,这时体积分数的取值范围满足
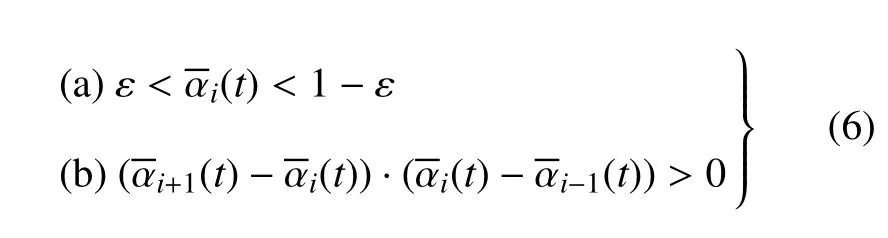
式中,ε为一个小量,可取为10−3.条件(a)定义了界面处体积分数的取值区间,条件(b)定义了界面的单调性.
在界面处体积分数从0变化到1,THINC方法选用双曲正切函数来模拟界面的变化趋势,如图1所示.对于固定的时间t和空间单元x∈[xi−1/2,xi+1/2],有从0到1的曲线
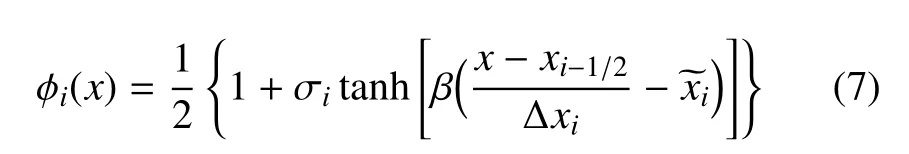
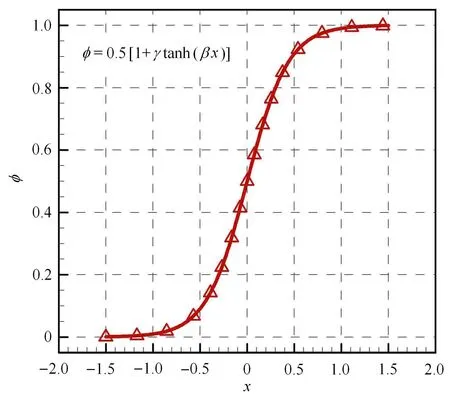
图1 双曲函数的变化规律Fig.1 Hyperbolic tangent function with x
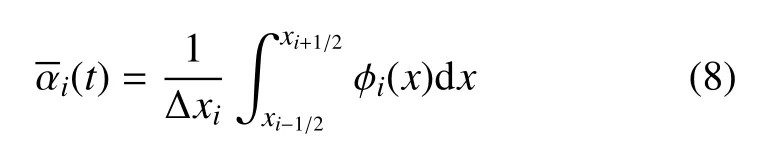
求解方程(8)可得
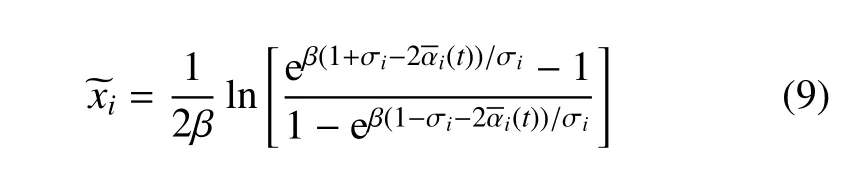
于是可知,包括体积分数重构在内,任何物理量的重构过程如下
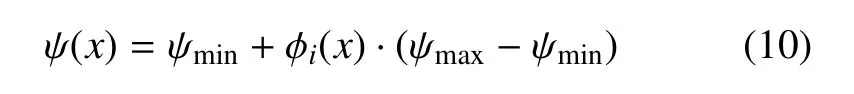
式中
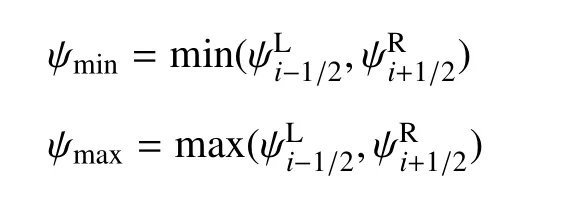
2 基于双界面函数的界面重构方法
由上述可知,THINC方法的构造过程保证了重构后体积分数的守恒性,但一次积分后双曲正切函数变得较为复杂.本文的研究在考察不同界面函数对界面重构效果的同时,也提供一种向多维扩展的可能性.与单界面函数不同,双界面函数在一个子网格内采用两个函数来重构界面.对于双界面重构方法,多种界面函数可供选择,本文以双正弦界面函数的界面重构方法DSINC为例来详细介绍双界面函数的构造过程.如图2所示,DSINC方法采用两条连续的正弦函数来重构界面,两个函数可以存在一阶间断,间断点位于单元体的中心.图2中,HL(x)定义为左正弦函数,HR(x)定义为右正弦函数,Cj为一阶间断点.下面给出界面重构后左右状态的推导过程.
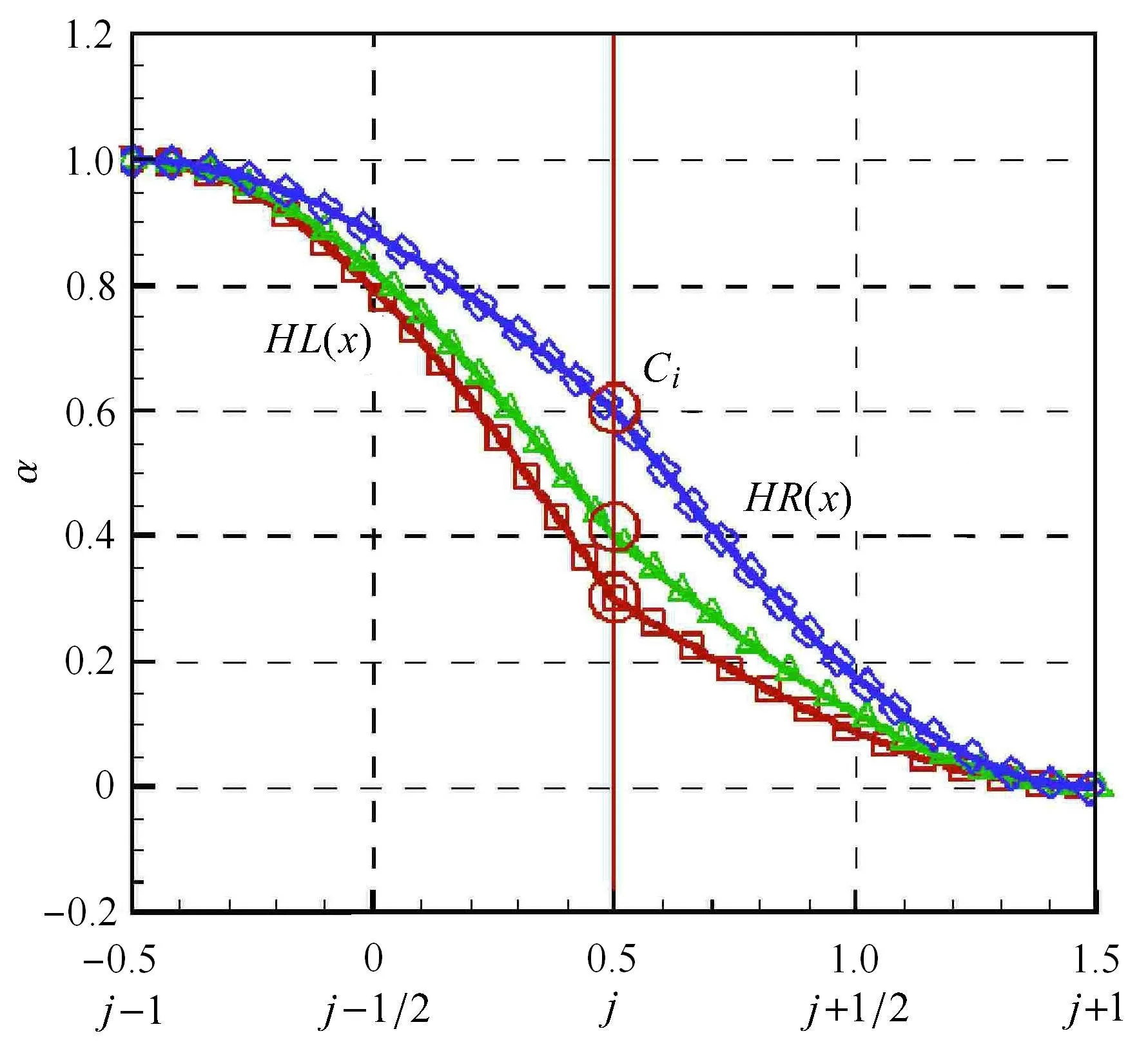
图2 DSINC界面重构示意图Fig.2 The illustration of interface functions used by DSINC
由于HL(x)和HR(x)连结了0和1,易知其函数形式为
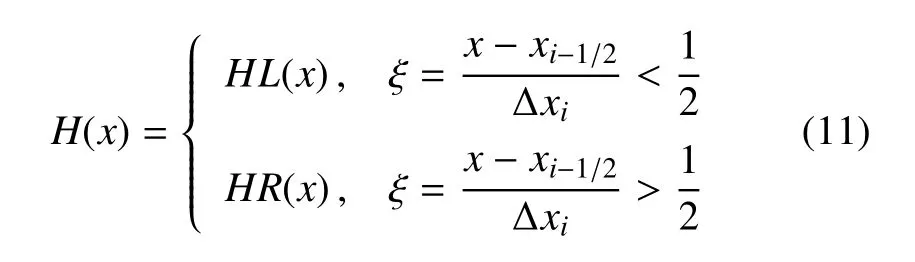
若设定i为单元体的中心索引,在保证界面函数连续的情况下,对于上升界面,即当时,则
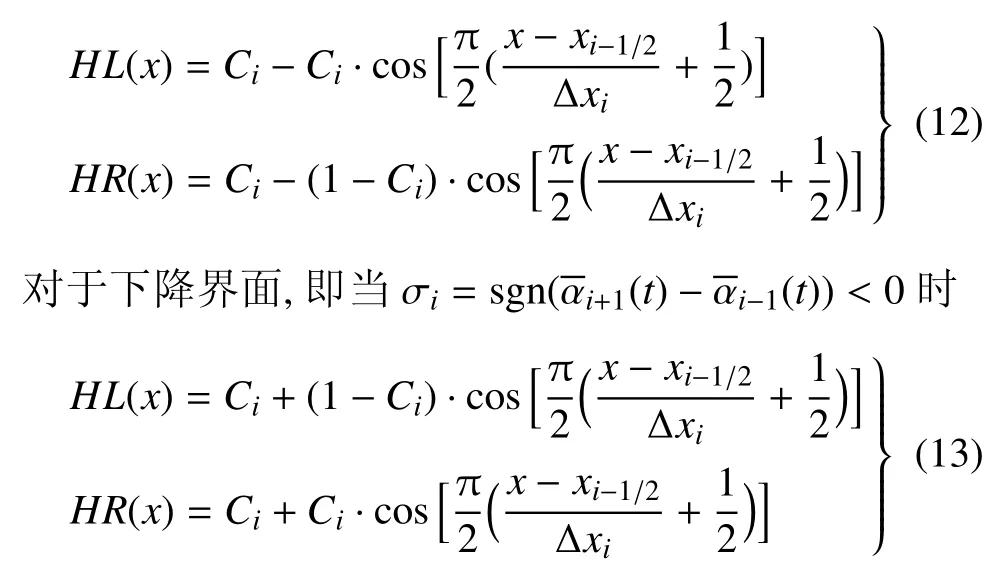
重构后的界面需保证体积分数守恒,即有
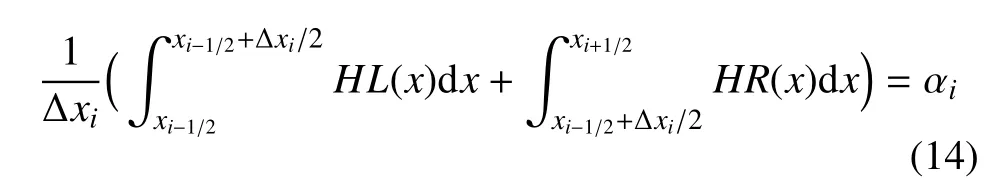
将方程(12)和方程(13)代入方程(14)可以求得连结点Ci的位置.经求解可得,上升界面(σi>0)与下降界面(σi<0)具有相同的积分结果
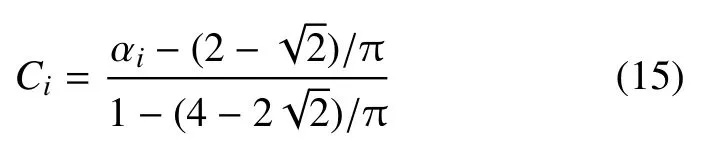
于是可知,采用DSINC方法重构界面后,左右状态分别为:
当σi>0时,有
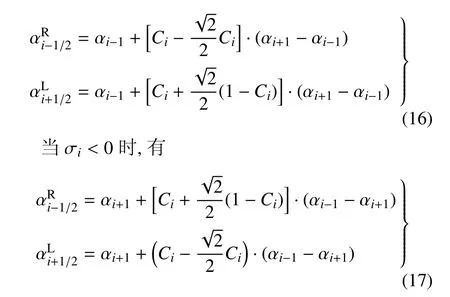
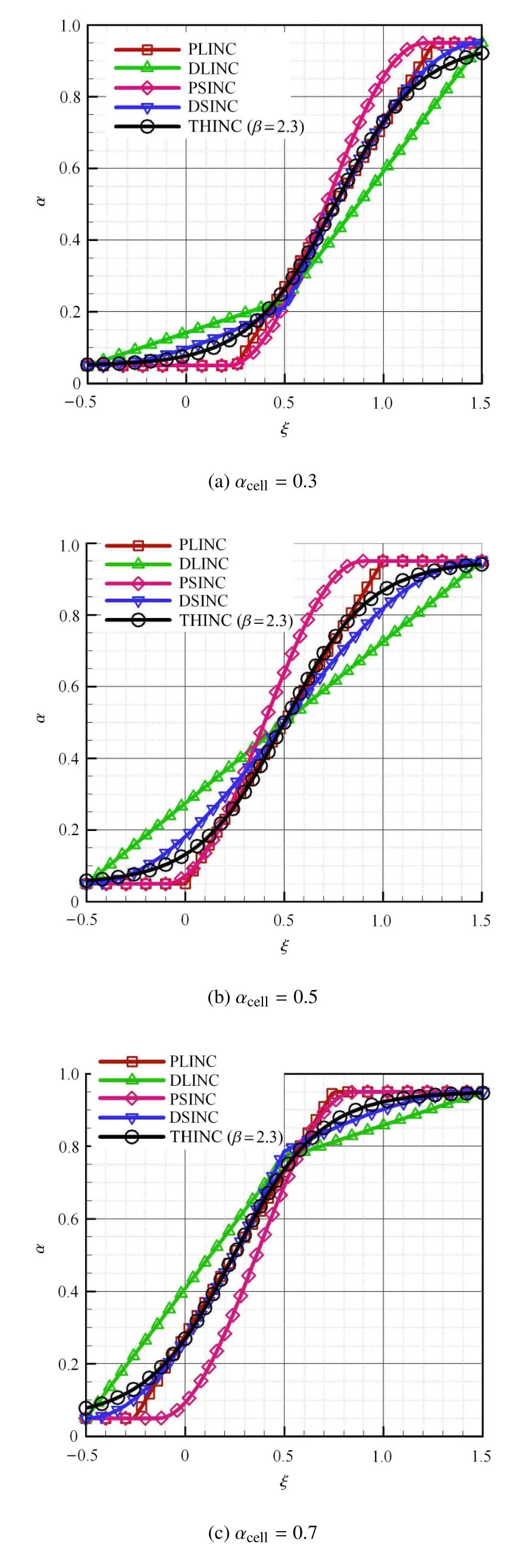
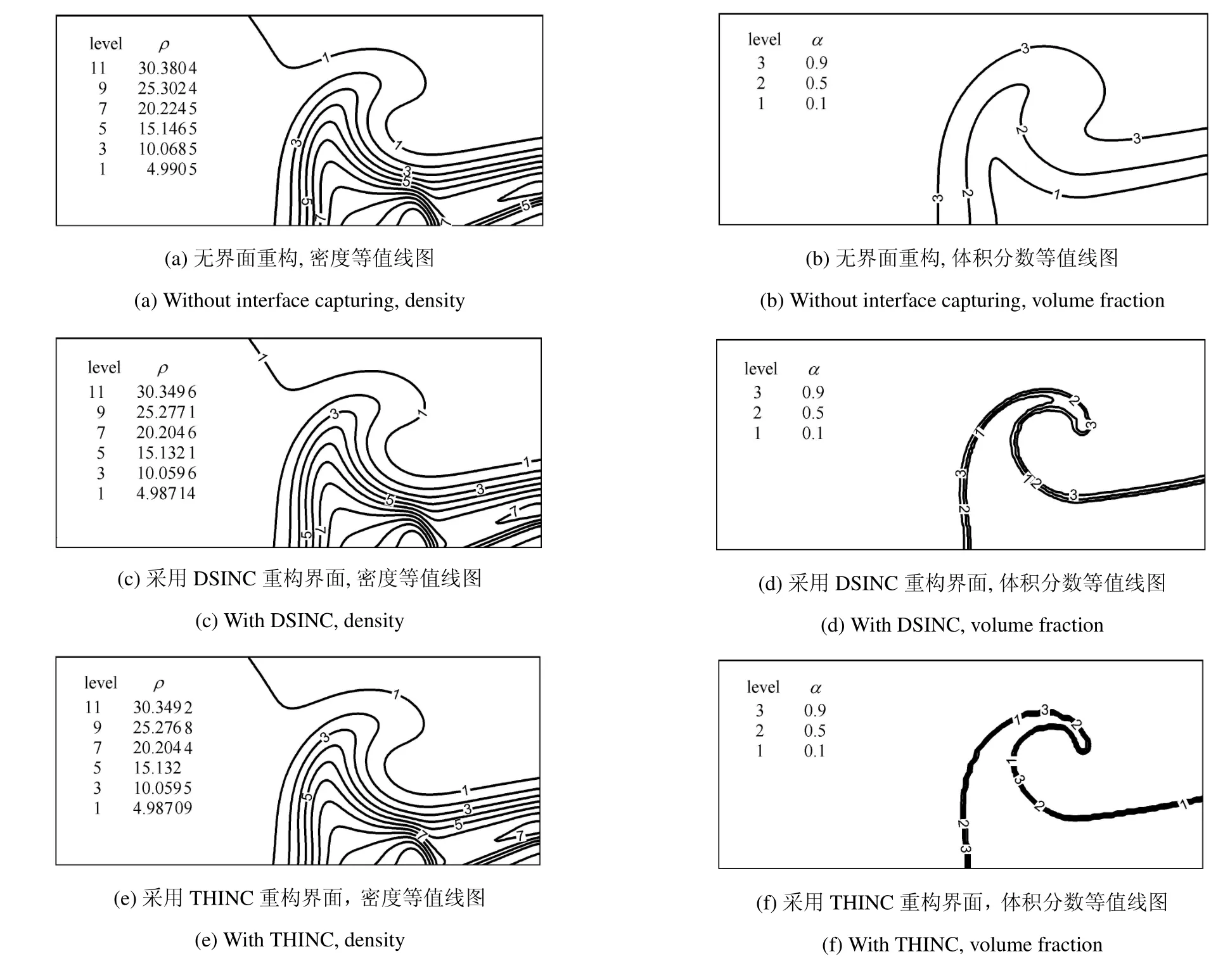
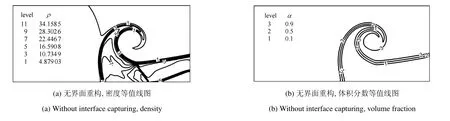
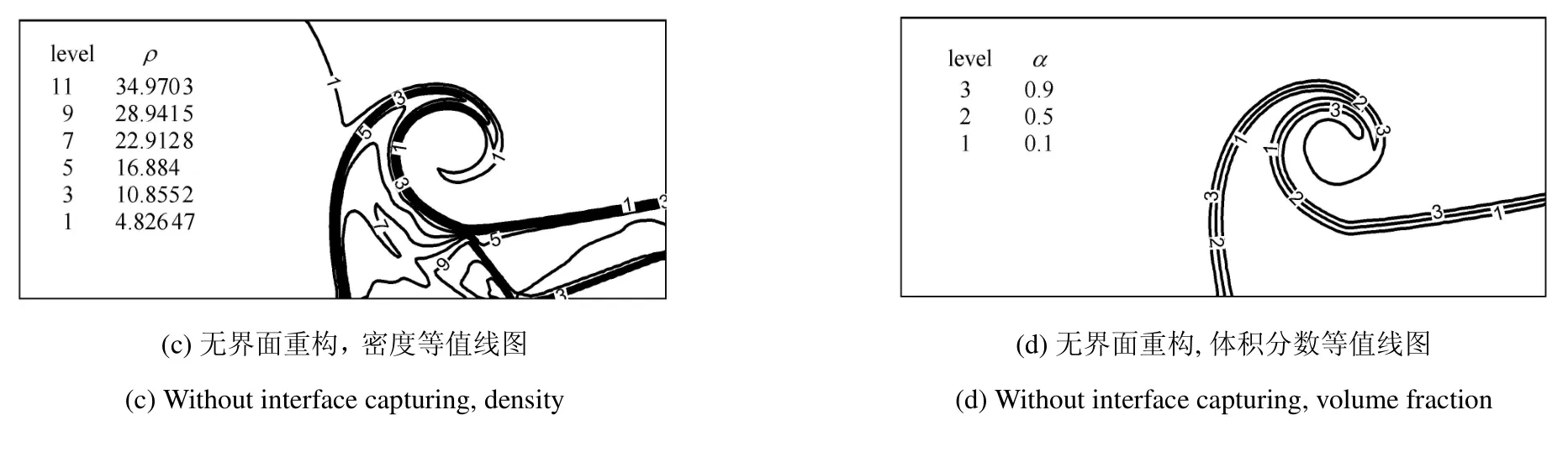
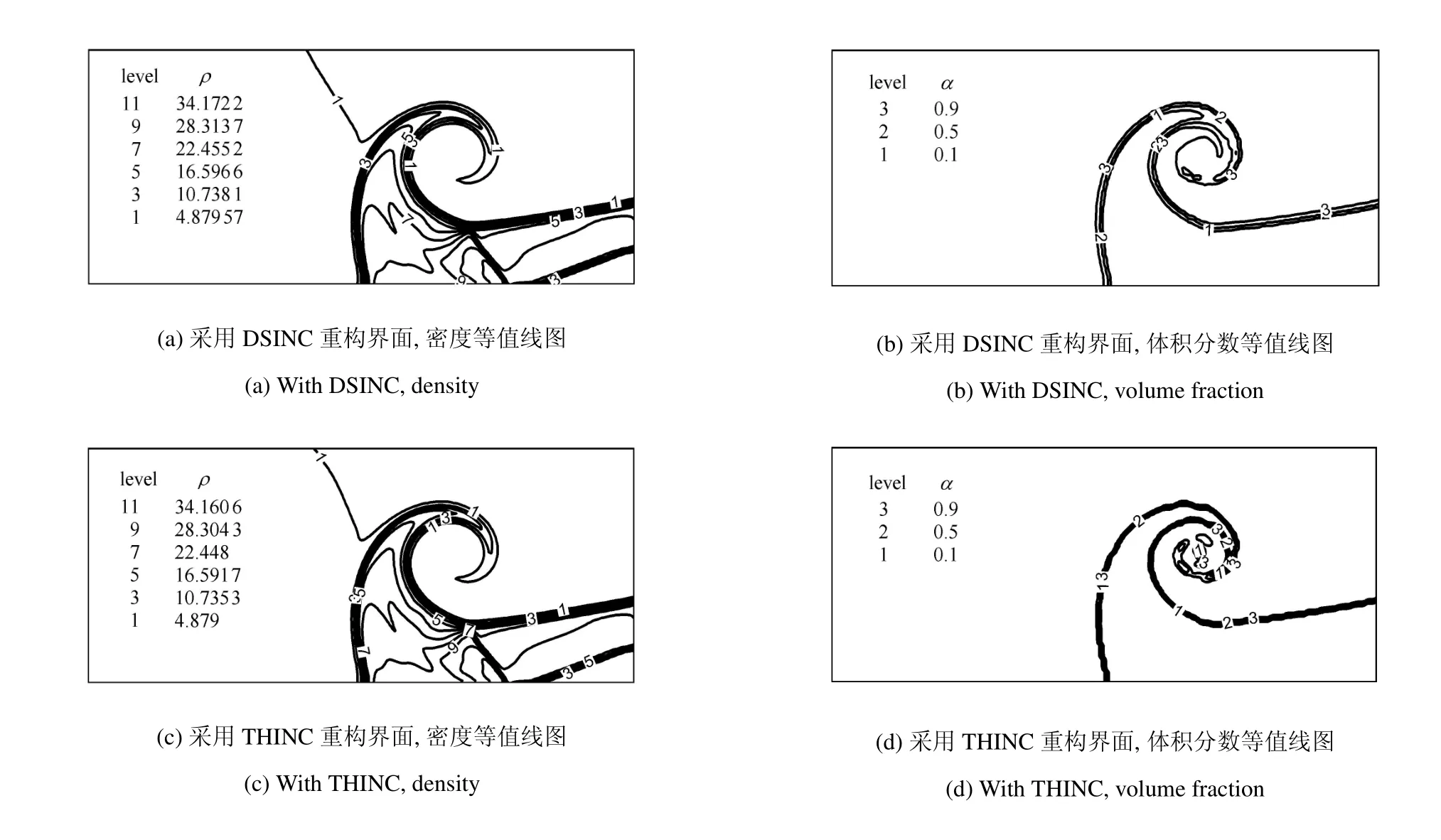
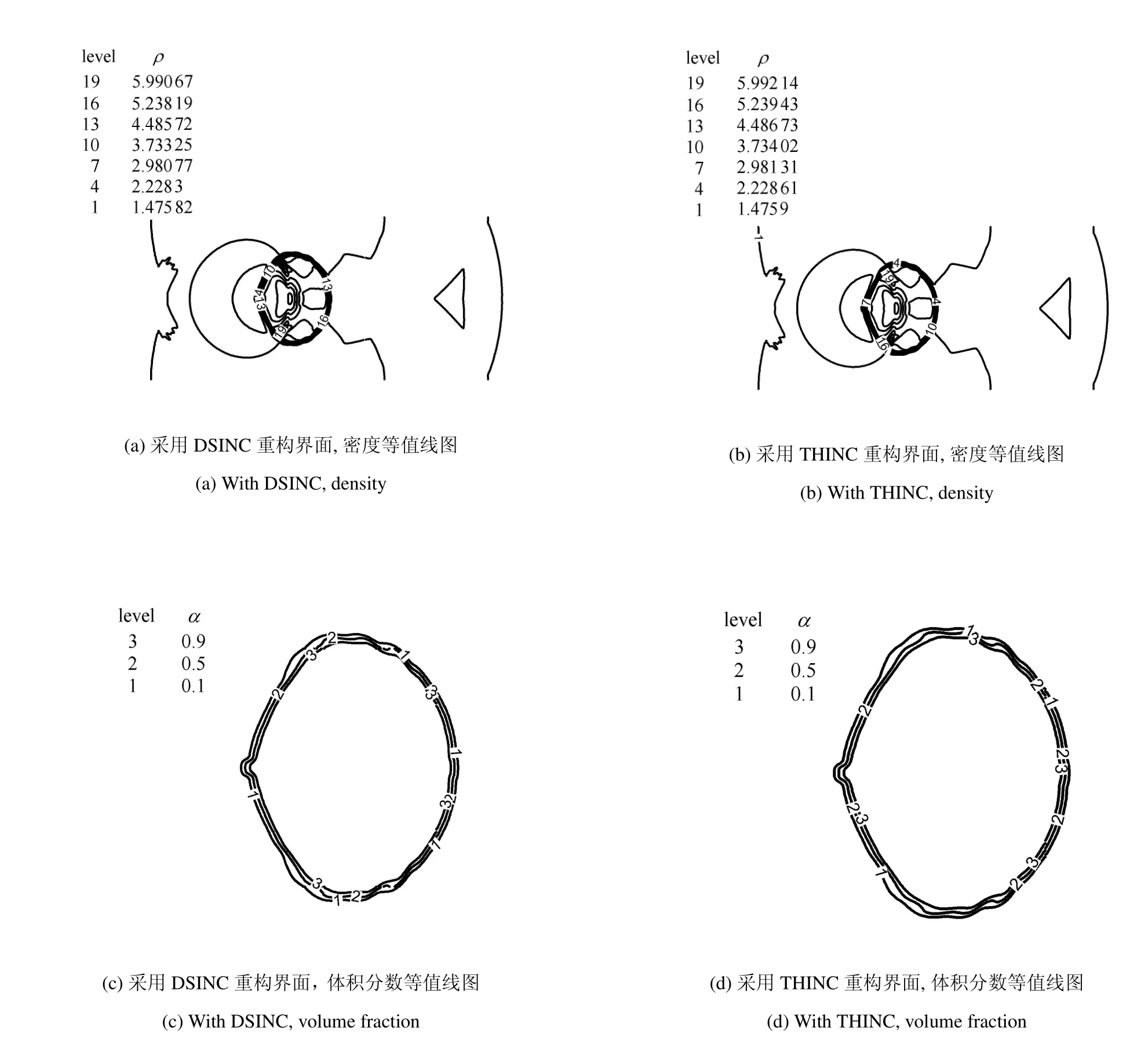
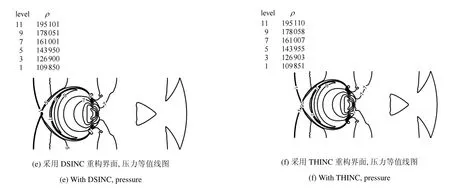
需要指出的是,由Cj的意义可知,0 此时,界面重构后的左右状态分别为 此时,界面重构后的左右状态分别为 此时,界面重构后的左右状态分别为 此时,界面重构后的左右状态分别为 基于以上重构思想,同样可以得到双线性界面重构方法 (double linear interface capturing,DLINC).对于单界面函数重构方法和双界面函数重构方法,图 3给出了单界面函数以及双界面函数在不同单元体中心体积分数值时的分布规律,其中ξ=(x−xi−1/2)/(xi+1/2−xi−1/2),而αcell为计算所得单元体中心值.对于THINC方法来说,反映界面斜率的参数β取2.3.从界面函数的分布规律来看,PSINC方法的界面最为陡峭,PLINC次之,THINC最为平缓,而DSINC的界面函数平缓度位于PLINC和THINC之间,界面函数的特性在一定程度上决定了界面捕捉的效果. 图3 界面重构后界面函数α随空间位置的变化Fig.3 The distribution of interface function in a cell under di ff erent cell value 方法测试的数值计算基于作者所在课题组开发的可压缩流体有限差分程序(code of fi nite di ff erence forcompressible fl uiddynamics,CFD2)开展.CFD2程序包含多种高阶方法,如WENO,MP和MUSCL等,通量的求解可选用Steger-Warming(SW),Lax-Friedrichs(LF)或者HLL黎曼求解器.考虑到本文所研究的主要内容为数值方法的对比,选用五阶WENO方法来求解左、右特征状态,用HLL方法来求解通量.在界面方法的验证中,在界面位置,WENO方法用THINC或DSINC方法来代替,流场中其他位置的求解保持不变. 为了研究所构造的界面方法对界面的捕捉效果,首先模拟了典型的圆形水柱的对流问题.计算区域(x,y)∈[0,2]m×[0,2]m,圆形水柱的初始位置为(0.5,0.5)m,水柱的半径R为0.25m,对流速度设为常数(ux,uy)=(100,100)m/s.此问题中,水的密度为ρ1=1000kg/m3,周围空气的密度为ρ2=1kg/m3.对于状态方程,参数选取为:对于水相,γ1=4.4,c01=1624.8m/s,ρ01=1000kg/m3;对于气相,γ2=1.4,c02=0,ρ02=1kg/m3.边界条件设为周期边界.在计算中,x,y方向的网格数均为100,计算CFL数取为0.2. 图4∼图6分别给出了计算300时间步后无界面重构方法、THINC方法和DSINC方法所得水柱界面体积分数分布.在不采用界面重构方法时,界面随着计算时间的延长而逐渐变宽,即使采用高阶格式,界面依然在逐渐耗散,如图4所示.对于THINC格式来说,无论是低阶还是高阶格式,界面均可以保持一种锐利(sharp)的效果.图6所给出的DSINC的计算结果,在低阶时,界面可以保持锐利,而高阶时界面捕捉效果更好. 图4 无界面重构时圆柱对流数值模拟结果Fig.4 Numerical results of water column problems without interface reconstruction 图5 THINC界面重构下圆柱对流数值模拟结果Fig.5 Numerical results of water column problems with THINC 图6 DSINC界面重构下界面重构数值结果Fig.6 Numerical results of water column problems with DSINC 两相三波点问题的计算区域为(x,y)∈[0,7]×[0,3],计算网格数为210×90,其他计算参数依照文献[11]来设置.图7给出了一阶精度下流场中的密度和体积分数分布.结果显示,在无界面重构方法时,流场中密度和体积分数分布逐渐变宽,以至于界面变得十分模糊.在采用界面重构方法时,对于体积分数来说,DSINC和THINC方法均能获得较为清晰的界面.同时,对比密度和体积分数的分布表明,体积分数的耗散来源于非守恒方程,而密度的耗散来自于连续方程,即使计算中采用体积分数去修正了流场中的状态分布,密度的耗散依然十分严重.在高阶格式下,所得密度和体积分数分布如图8(a)和图8(b)所示.而对于体积分数分布来说,采用高阶格式可以获得较为清晰的界面,但界面依然在逐渐耗散.这一结论与圆形水柱对流的计算结果较为一致.HLL通量方法本身具有一定的耗散性,为了分析这种特性,图8(c)和图8(d)给出了采用HLLC方法模拟三波点问题的数值结果.结果显示,对于所模拟的问题来说,结果仅在半圆形的界面处存在有限的改善.这表明,在两相流问题的数值模拟中,获得清晰的界面捕捉效果仍需对界面采用界面捕捉格式进行处理. 采用五阶精度数值格式和THINC/DSINC界面方法来模拟的两相三波点问题如图9所示.在高阶格式下,对比图7发现,采用DSINC和THINC依然均可以使得界面保持锐利的捕捉效果.进一步分析发现,相比THINC方法,DSINC方法略带耗散.Xiao等[16]分析了界面函数变化趋势以及在界面函数下所产生的耗散性,依据其分析结果可知,DSINC所产生的略大的界面耗散性是由界面函数的特点所引起. 图7 一阶精度下两相三波点问题密度和体积分数分布Fig.7 Density and volume fraction distributions for two-phase triple point problems using 1st order scheme 图8 两相三波问题五阶精度下采用HLL和HLLC所得密度和体积分数分布的对比((a)和(b)采用HLL格式计算,(c)和(d)采用HLLC格式计算)Fig.8 Density and volume fraction distributions using 5th WENO+HLL/HLLC methods(HLL is used in(a)and(b),HLLC is used in(c)and(d)) 图8 两相三波问题五阶精度下采用HLL和HLLC所得密度和体积分数分布的对比((a)和(b)采用HLL格式计算,(c)和(d)采用HLLC格式计算)(续)Fig.8 Density and volume fraction distributions using 5th WENO+HLL/HLLC methods(HLL is used in(a)and(b),HLLC is used in(c)and(d))(continued) 图9 五阶精度下两相三波问题DSINC和THINC所得密度和体积分数分布的对比((a)和(b)采用HLL格式计算,(c)和(d)采用HLLC格式计算)Fig.9 Density and volume fraction distributions using 5th WENO and DSINC/THINC methods(HLL is used in(a)and(b),HLLC is used in(c)and(d)) 激波界面相互作用问题是两相流数值模拟中另一个典型的问题[22],其中激波气泡相互作用问题经常用作数值验证和实验对比分析[23-24].在本文的数值模拟中,气泡内的气体为R22,周围为空气.在初始时刻,马赫数为1.22的左行激波位于x=275mm处,而气泡的半径R=25mm,位于(x,y)=(225,44.5)mm之处.R22气体采用理想气体模型:γ1=1.249,ρ01=3.863kg/m3;空气的相应参数为:γ2=1.4,ρ02=1.225kg/m3.在气泡内,流场初始变量设为 激波后区域 其他区域 在此问题的模拟中,计算区域的大小为(x,y)∈[0,445]×[0,89]mm,计算网格数为1780×178.数值模拟结果如图10所示.计算中除所采用的界面方法不同外,其他条件均相同.从图中可以看出,对于相同的时间(t=0.3ms)的计算结果,DSINC和THINC方法所得结果略有差异.从计算结果来看,较长时间的数值模拟之后,密度所表示的界面依然可以清晰分辨出来,两种方法所计算的体积分数等值线较为相似,界面较为清晰.由此可知,对于本文所构造的双正弦界面重构方法来说,可以获得与THINC相当的计算效果. 图10 采用DSINC和THINC界面方法所得密度、体积分数和压力等值线图对比Fig.10 Density,volume fraction and pressure distributions using DSINC and THINC interface methods 图10 采用DSINC和THINC界面方法所得密度、体积分数和压力等值线图对比(续)Fig.10 Density,volume fraction and pressure distributions using DSINC and THINC interface methods(continued) 本文的研究发展了一种新的双界面函数重构方法,并基于此思想采用双正弦函数构造了双正弦界面重构方法DSINC.随后在数值方法的验证中,采用作者所在课题组发展的CFD2程序,分别对比了一阶、五阶精度数值模拟中无界面重构、DSINC界面重构和THINC界面重构计算结果的不同.从圆柱对流问题、两相三波点问题和激波与界面相互作用问题的对比发现,DSINC与THINC出现了基本一致的界面重构效果.另外,双界面函数重构时,由于函数的易于积分的特性,左、右特征变量并没有出现复杂的表达式,这一特点使其更易于向多维扩展. 1 赵宁,王东红.多介质流体界面问题的数值模拟.北京:科学出版社,2016(Zhao Ning,Wang Donghong.Numerical Simulation of Multimaterial Fluid Interface Problems.Beijing:Science Press,2016(in Chinese)) 2 Jesus WC,Roma AM,Pivello MR,et al.A 3D front-tracking approach for simulation of a two-phase fl uid with insoluble surfactant.Journal of Computational Physics,2015,281(c):403-420 3 Terashima H,Tryggvason G.A front-tracking/ghost- fl uid method for fl uid interfaces in compressible fl ows.Journal of Computational Physics,2009,228(11):4012-4037 4 Tryggvason G,Bunner B,Esmaeeli A,et al.A front-tracking method for the computations of multiphase fl ow.Journal of Computational Physics,2001,169(2):708-759 5 Lu H,Zhao N,Wang D.A front tracking method for the simulation of compressible multimedium fl ows.Communications in Computational Physics,2016,19(1):124-142 6 ScardovelliR,ZaleskiS.Directnumericalsimulationoffree-surface and interfacial fl ow.Annu Rev Fluid Mech,1999,31(1):567-603 7 Torres DJ,Brackbill JU.The point-set mothod:front-tracking without connectivity.Journal of Computational Physics,2000,165(2):620-644 8 Fedkiw RP,Sapiro G,Shu C-W.Shock capturing,Level sets and PDE based methods in computer vision and image processing:A review of Osher’s constributions.Journal of Computational Physics,2003,185(2):309-341 9 Sussman M,Smereka P,Osher S.A level set approach for computing solutions to incompressible two-phase fl ow.Journal of Computational Physics,1994,114(1):146-159 10 Fleckenstein S,Bothe D.A volume-of- fl uid-based numerical method for multi-component mass transfer with local volume changes.Journal of Computational Physics,2015,301(c):35-58 11 Shyue K-M,Xiao F.An Eulerian interface sharpening algorithm for compressible two-phase fl ow:The algebraic THINC approach.Journal of Computational Physics,2014,268(2):326-354 12 Susman M,Puckett EG.A coupled level set and volume-of- fl uid method for computing 3d and axisymmetric incompressible twophase fl ows.Journal of Computational Physics,2000,162(2):301-337 13 So KK,Hu XY,Adams NA.Anti-di ff usion method for interface steepening in two-phase incompressible fl ow.Journal of Computational Physics,2011,230(13):5155-5177 14 So KK,Hu XY,Adams NA.Anti-di ff usion interface sharpening technique for two-phase compressible fl ow simulations.Journal of Computational Physics,2012,231(11):4304-4323 15 Youngs DL.An interface tracking method for a 3D Eulerian hydrodynamics code.Technical Report 44/92/35,AWRE,1984 16 Xiao F,Honma Y,Kono T.A simple algebraic interface capturing scheme using hyperbolic tangent function.International Journal for Numerical Methods in Fluids,2005,48(9):1023-1040 17 Xiao F,Li S,Chen C.Revisit to the THINC scheme:A simple algebraic VOF algorithm.Journal of Computational Physics,2011,230(19):7086-7092 18 Li S,Sugiyama K,Takeuchi S,et al.An interface capturing method with a continuous function:The THINC method with multidimensional reconstruction.Journal of Computational Physics,2012,231(5):2328-2358 19 Cassidy DA,Edwards JR,Tian M.An investigation of interfacesharpening schemes for multi-phase mixture fl ows.Journal of Computational Physics,2009,228(16):5628-5649 20 Toro EF.Riemann Solvers and Numerical Methods for Fluid Dynamics(Third Edition).Berlin,Heidelberg:Springer-Verlag,2009 21 Johnsen E,Colonius T.Implementation of WENO schemes in compressible multicomponent fl ow problems.Journal of Computational Physics,2006,219(2):715-732 22 蒋华,董刚,陈霄.小扰动界面形态对RM不稳定性影响的数值分析.力学学报,2014,46(4):544-552(Jiang Hua,Dong Gang,Chen Xiao.Numerical study on the e ff ects of small-amplitude initial perturbations on RM instability.Chinese Journal of Theoretical and Applied Mechanics,2014,46(4):544-552(in Chinese)) 23 王革,关奔.激波作用下R22气泡射流现象研究.力学学报,2013,45(5):707-715(Wang Ge,Guan Ben.A study on jet phenomenon of R22 gas cylinder under the impact of shock wave.Chinese Journal of Theoretical and Applied Mechanics,2013,45(5):707-715(in Chinese)) 24 王显圣,司廷,罗喜胜等.反射激波冲击重气柱的RM不稳定性数值研究.力学学报,2012,44(4):666-674(Wang Xiansheng,Si Ting,Luo Xisheng,et al.Numerical study on the RM instability of a heavy-gas cylinder interacted with reshock.Chinese Journal of Theoretical and Applied Mechanics,2012,44(4):664-672(in Chinese)) A NEW INTERFACE CAPTURING METHOD BASED ON DOUBLE INTERFACE FUNCTIONS1) Li Kang*,†Liu Na*,†He Zhiwei*Luo Longshan*,†Tian Baolin*,2) Wedescribeanoveldouble-interface-function(DIF)reconstructionmethodforefficientnumericalresolutionof a compressible two-phase fl ow.Based on the new method,double sine interface capturing scheme(DSINC)is obtained.Five-equation model is solved to analyze the e ff ect of di ff erent interface functions such as DIF and Single Interface function(SIF)on the interfaces captured numerically.Near the interfaces,the algorithm uses the DIF or SIF as a basis for the reconstruction of a sub-grid discontinuity of volume fractions.In regions away from the interfaces,WENO is used to reconstruct the convective term,and time integration of the algorithm is done by employing the TVD Runge-Kutta method.Comparing with tangent of hyperbola for interface capturing(THINC)using SIF method,the left and right states reconstructed by DSINC is simpler and we need not solve a transcendental equation.Numerical results are shown with the Mie-Grneisen equation of state(EOS)for sample problems such as discontinuous advection,two-phase triple problem and shock-bubble interaction problem with THINC and DSINC.It can be found that DSINC is able to get as efficient resolution interface as THINC and shows to be more stable in the simulation. multi-phase fl ow,interface capturing,THINC,double interface functions reconstruction,DSINC O359+.1 A doi:10.6052/0459-1879-17-210 2017–09–04 收稿,2017–09–12 录用,2017–09–13 网络版发表. 1)国家自然科学基金资助项目(11472059,U1630247,1730111). 2)田保林,研究员,主要研究方向:计算流体力学数值方法.E-mail:tian_baolin@iapcm.ac.cn 李康,刘娜,何志伟,骆龙山,田保林.一种基于双界面函数的界面捕捉方法.力学学报,2017,49(6):1290-1300 Li Kang,Liu Na,He Zhiwei,Luo Longshan,Tian Baolin.A new interface capturing method based on double interface functions.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1290-1300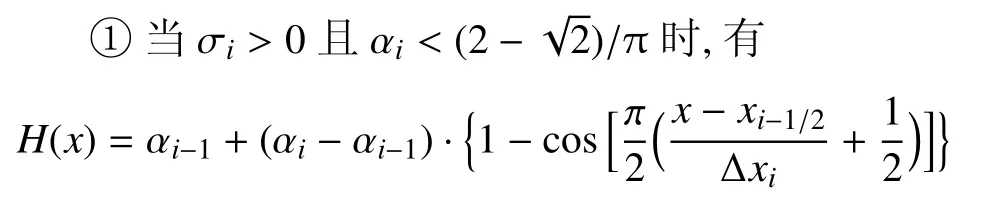
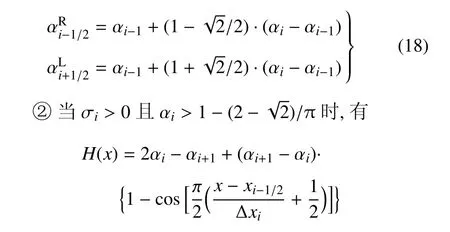
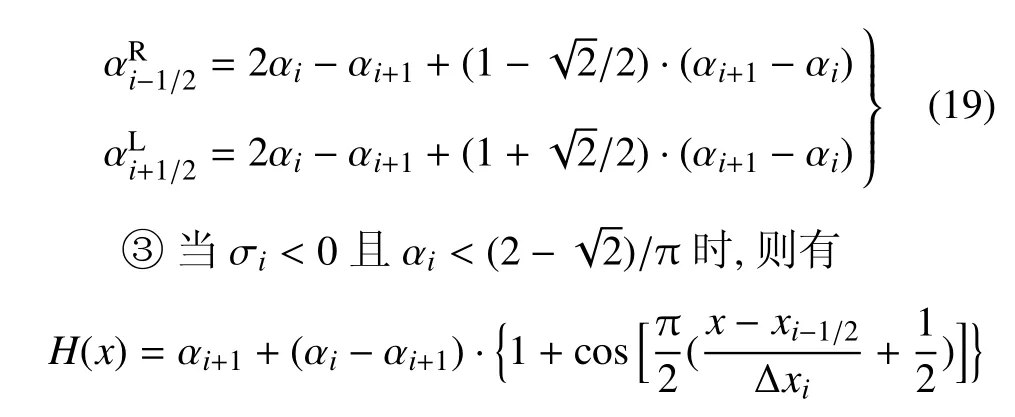
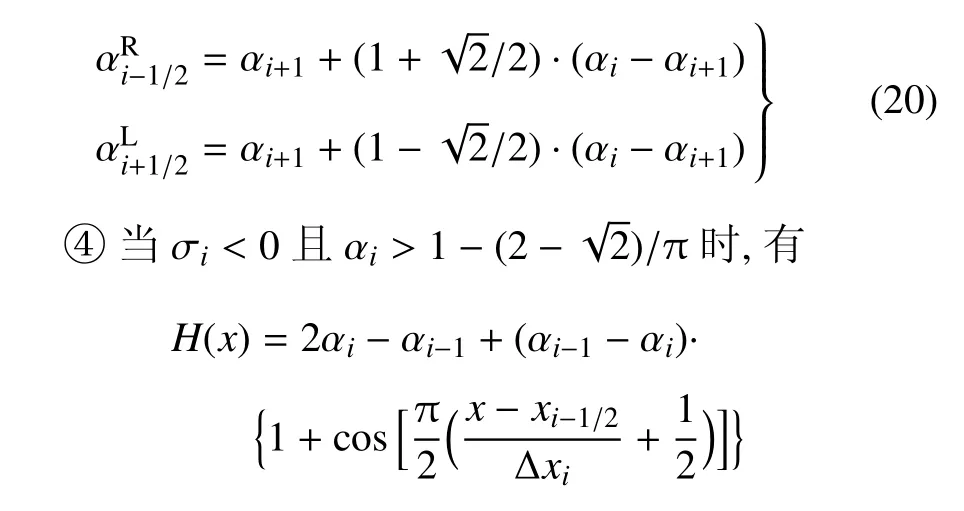
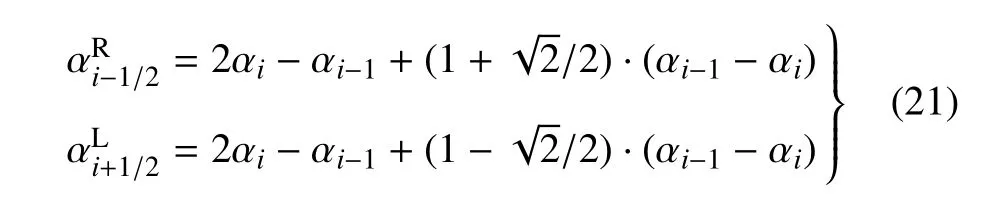
3 数值结果与分析
3.1 圆形水柱对流问题
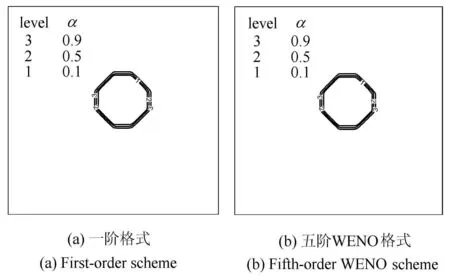
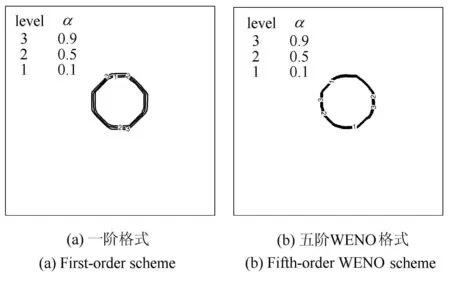
3.2 两相三波点问题
3.3 激波与气泡相互作用问题
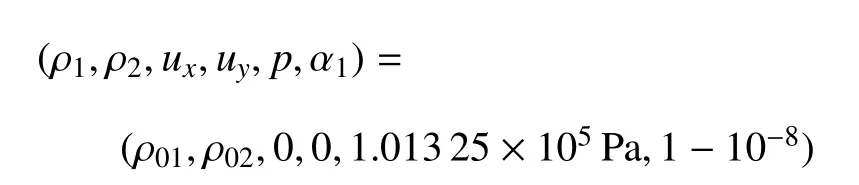
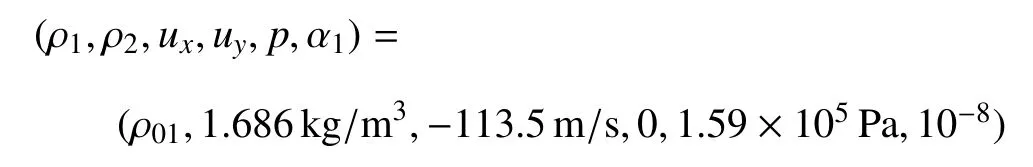
4 结论
*(Institute of Applied Physics and Computational Mathematics,Beijing100088,China)
†(CAEP Software Center for High Performance Numerical Simulation,Beijing100088,China)
