矩形疏水沟槽表面水滴振荡特性1)

董琪琪 胡海豹,†,2) 陈立斌 余思潇

*(西北工业大学航海学院，西安710072)

†(西北工业大学深圳研究院，深圳518057)

矩形疏水沟槽表面水滴振荡特性1)

董琪琪*胡海豹*,†,2)陈立斌*余思潇*

*(西北工业大学航海学院，西安710072)

†(西北工业大学深圳研究院，深圳518057)

液滴振荡行为是液滴运动中的重要伴随现象,具有重要科研价值.由于液滴撞击疏水沟槽板时运动行为与光滑表面明显不同，可以推测疏水沟槽表面液滴振荡特性也将会呈现与众不同的行为特点.采用高速摄像技术，研究了矩形疏水沟槽表面上水滴高度和接触线振荡行为随沟槽尺寸和撞击速度的变化规律.结果发现，矩形疏水沟槽造成的各向润湿异性使得振荡过程中水滴在平行沟槽方向上的接触线长度大于垂直方向，但并不影响水滴高度方向上衰减振荡的周期，即水滴振荡周期与沟槽间距无关；同时由于疏水沟槽表面上存在能垒束缚效应，致使水滴振荡过程中接触线的铺展和回缩运动不服从典型阻尼振荡规律，而呈现振荡数次后直接趋稳的特点.如水滴以0.61m/s撞击时，接触线经历2次振荡后即维持稳定，但此时水滴仍在持续振荡中.另外，还初步分析了水滴振荡周期与沟槽间距无关的原因.

矩形疏水沟槽，水滴，振荡，三相接触线

引言

液滴撞击壁面的现象出现在很多工程应用中,例如喷墨打印、喷涂、喷雾冷却、电缆结冰等[1-8].当液滴撞击在润湿壁面后，会出现铺展、振荡、破裂、反弹等现象[9-16]，具有重要科研价值.其中，液滴振荡行为已经被用于提高DNA微数列荧光性[17]和测量水滴表面张力和黏度[18].

在液滴振荡试验研究方面，Wang等[19]发现液滴在玻璃壁面振荡三个周期(0.085s)后达到平衡，而在石蜡壁面却能持续 28个周期(0.266s).Wang等[20]发现壁面润湿性和液滴撞击速度对液滴振荡高度影响较明显，而表面活性剂对其影响较弱.Banks等[21]则提出亲水性表面阻碍液滴振荡，而疏水表面能维持振荡，且低黏度液滴振荡时间比高黏度液滴更长.通过数值模拟，Miller等[22]分析了黏性振荡液滴浸入到另一种液体时的色散方程，通过小振荡的频率和阻尼率可以计算出液滴尺寸和界面黏弹性系数.Prosperetti[23]利用Laplace变换，解决了当黏性效应不能忽略时，气泡和液滴在液体中的小振幅(线性)自由振荡所引起的初值问题.Tsamopoulos等[24]获得了无黏性、大幅度振动液滴的振幅振荡的一般理论，最明显的结果是液滴形状的振荡频率表现出随振幅的升高而降低，在小幅度理论中频率随幅度的变化而没有改变.Damir等[25]得出在真空中黏弹性液滴振荡的特征方程，从液体的性质上发现一些令人关注的问题.Zhang等[26]指出运动黏度对液滴振荡高度和速度的影响大于液滴表面张力.陈石等[10]则指出液滴的铺展半径在黏性力的作用下衰减振荡,并且黏性力越大,铺展半径衰减越快.液滴振荡最大铺展半径、高度随着液滴大小和初始铺展速度的增大而增大,而随着表面张力的增大而减小.液滴的振荡是等幅振荡,并且振幅随着表面张力的增大而减小,频率随着表面张力的增大而增大.

与光板润湿行为不同，Range等[27]研究了液滴对粗糙固体表面的撞击，发现水滴飞溅的最小韦伯数与水滴半径、表面粗糙度系数有关.Kannan等[28]发现，沟槽结构改变了液体薄片在沟槽表面上的形状.施瑶等[29]发现，在平板上加工规则的沟槽能有效改变壁面的润湿性，致使壁面润湿展现出各向异性.Hu等[30]发现在较高的冲击速度下，扩散过程是在平行于微沟槽的表面上进行的，在垂直于微沟槽的方向上反而被阻止.Song等[31]进一步发现液滴在部分微沟槽表面上时，平行于沟槽的接触角大于光滑表面上的接触角，而微观结构对垂直于沟槽的接触角影响不大.由上可知，液滴撞击疏水沟槽板时的运动行为与光滑表面明显不同.可以推测，疏水沟槽表面液滴振荡特性也将会呈现与众不同的行为特点.为此，本文重点研究矩形疏水沟槽壁面上水滴振荡特性，并初步分析其产生原因.

1 实验装置与方法

实验装置主要由采集计算机、微量泵、平头针、高速摄像机和试件等组成 (如图 1).其中，采集计算机用于实验数据记录、处理；平头针与微量泵连接，用于产生体积恒定的水滴；高速摄像机 (RED LAKE,IDT N4)用于水滴在平行和垂直于试件两方向的动态形态捕捉，采集频率为3000fps.同时,为观测水滴细微形态变化，这里给高速摄像机加装了显微镜头.实验图像则采用Image-Pro Plus软件进行处理.实验用水为去离子水，实验温度为20◦C.

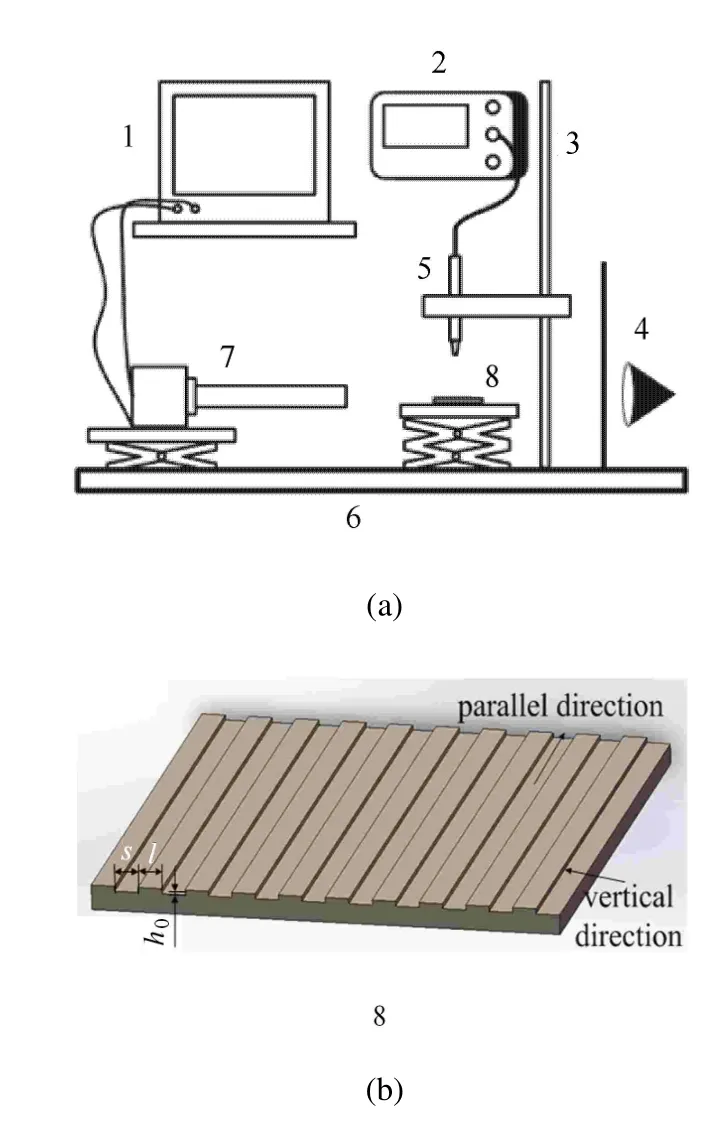
图1 实验装置简图1:采集计算机,2:微量泵,3:可调节支架,4:光源,5:平头针,6:移动导轨,7:高速摄像机(装配显微镜头),8:试件Fig.1 Schematic diagram of experimental apparatus 1:Acquisition computer,2:Micro pump,3:Adjustable frame,4:Light source,5:Flat face needle,6:Moving rail,7:High-speed camera(micro lens),8:Specimen

试件材料(图1(b))为黄铜，表面矩形沟槽采用LIGA-like技术加工，其中，s为槽宽度(s=0.5mm)，h0为槽深度 (h0=0.1mm)，l为槽间距 (l=0.2∼0.6mm).疏水化处理前，首先将沟槽试件分别在乙醇和丙酮中超声洗涤3次，然后用氧气等离子体处理2min以去除表面污染物.然后将其浸入大分子引发剂溶液中(溶剂为DMF)，室温避光条件下浸泡24h后，取出并用大量DMF和乙醇冲洗以除去表面物理吸附的聚合物，然后用氮气流吹干.最后，分别取适量GO悬浮水和CNTs粉末加入1.0mg/mL的大分子引发剂溶液中，并在室温避光下搅拌24h后离心分离，再分别用DMF和乙醇离心洗涤2次以除去物理吸附的引发剂.经过以上步骤，便可以获得稳定的疏水性沟槽壁面.对不同矩形疏水沟槽试件上水滴静态接触角进行测试，发现接触角的变化呈规律性的波动，且垂直沟槽方向上接触角始终大于平行沟槽向(图2),这与文献[29]中的结论基本一致，而具体波动的原因有待进一步研究.

图2 矩形疏水沟槽壁面上静润湿状态随槽间距l的变化规律Fig.2 The variation of wetting state with the width of the slot l on the rectangular hydrophobic grooves

2 结果与分析

2.1 水滴撞击振荡过程

与文献报道一致[9-16]，随撞击韦伯数We的增大，疏水沟槽壁面上水滴会呈现出铺展、弹跳、和破碎等不同行为.当We6 13.13时，水滴会经历多次铺展和收缩过程，即呈现不稳定的振荡过程.图3为直径为2.57mm水滴以U=0.44m/s的速度撞击到槽间距l=0.2mm沟槽壁面上的振荡过程.其中，图3(a)为垂直于沟槽方向水滴振荡过程，图3(b)为平行于沟槽方向水滴振荡过程，这里t=0为水滴接触壁面的瞬时.可以发现，在0∼25.0ms期间，水滴外形变化幅度很大，呈现快速衰减特征.其中，在t=1.7ms时，水滴呈葫芦状，即下半部分为半径较大的椭球状，上半部分为半径较小的椭球状.t=4.7ms时，水滴中心部分则呈锥型.t=6.7ms时，水滴中心出现一股反冲向水滴内部的射流.t=11.3ms时，水滴高度达到最高.随后，在t为25∼166ms期间，水滴外形则无大幅度变化，呈现缓慢衰减振荡特征(因该过程持续很多个振荡周期，图3中仅给出4张典型水滴状态照片).同时可以看出，在平行和垂直于沟槽方向上,虽然振荡现象相似，但平行向水滴接触线的长度要长于垂直向(图中垂直向接触线的宽度等于白色细线长度，而平行向接触线的宽度大于白色细线长度).这与垂直沟槽向的静态接触角大于平行沟槽向上静态接触角的规律正好对应，说明垂直沟槽方向上存在更大能量壁垒(能垒)，即沟槽对其垂直方向上接触线移动的束缚更强.

图3 水滴撞击矩形疏水沟槽表面的典型振荡形态Fig.3 Typical shapes of water droplet impinging on the surface of rectangular hydrophobic grooves

2.2 水滴高度振荡

为观察典型矩形疏水沟槽上水滴振荡周期的变化，这里详细统计了10种不同沟槽上水滴振荡高度的变化情况，图4仅给出了槽间距l为0.2mm，0.6mm，1.0mm时矩形疏水沟槽壁面上水滴高度的振荡曲线.从中也可以清晰发现，水滴高度振荡可分为快速衰减振荡阶段和缓慢衰减振荡阶段.为准确提取水滴振荡周期信息，文中采用线性衰减振荡函数对第二振荡阶段进行数值拟合，即弃用前两个振荡周期的试验数据，而选取从第三个振荡周期开始的试验数据来拟合.采用拟合函数表达式为

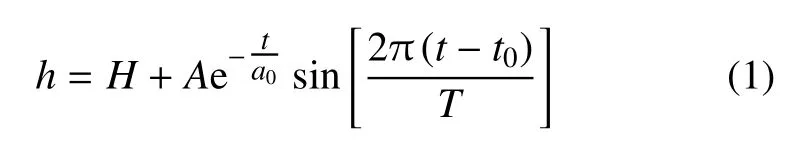
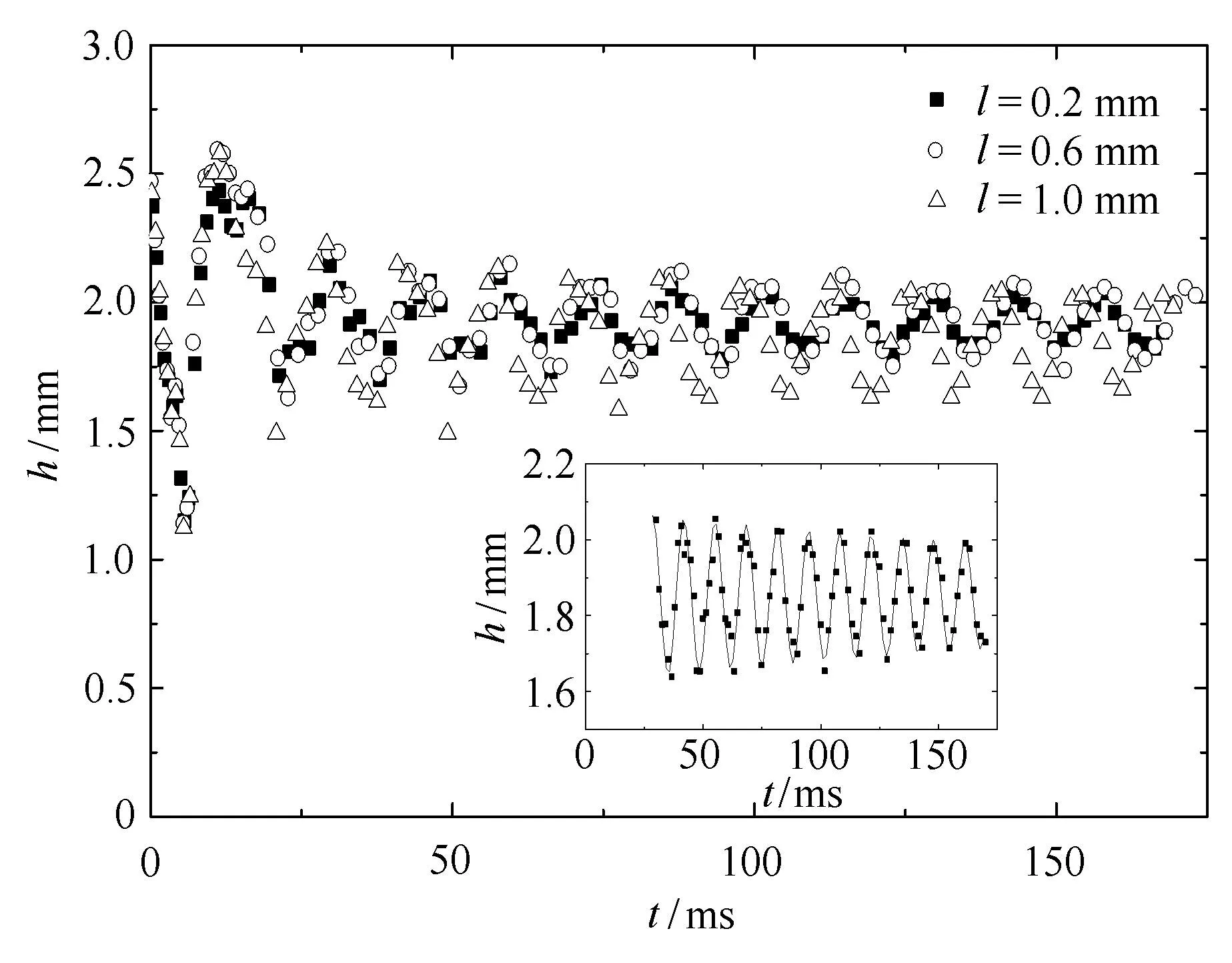
图4 典型矩形疏水沟槽壁面上水滴高度振荡(中小图为槽间距l=0.2mm壁面上振荡拟合曲线)Fig.4 Oscillation of the water droplet in the height direction on the surface of the typical rectangular hydrophobic grooves(Illustration is the curve fi tting for oscillation on the surface of l=0.2mm)

式中，H为液滴最终稳定高度，A为高度振荡幅值，a0为衰减模量(1/a0为衰减系数)，为圆频率(T为周期).图4内的插图为槽间距l=0.2mm矩形疏水沟槽壁面上水滴高度振荡拟合曲线，与试验数据吻合良好.

图5为拟合处理得到的矩形疏水沟槽壁面上水滴振荡周期T随槽间距l的变化关系.令人惊讶的是，水滴高度的振荡周期维持不变，即沟槽间距不影响水滴高度的振荡周期.

图5 水滴振荡周期T随槽间距l的变化Fig.5 The variation of water droplet oscillation period T with the width of the slot l

不同试件上沟槽间距和润湿性(平行向及垂直向润湿性)存在明显差异，却展示出几乎完全相同的振荡周期.为探索其原因，论文从疏水沟槽表面水滴体积及振荡周期的理论预测方面进行了详细分析.水滴稳定在疏水矩形沟槽壁面后呈现Cassie状态，这里假定水滴在垂直于沟槽壁面方向呈球缺状(图6(a))，而在平行方向呈椭球缺状(图6(b)).图6中，R2和R1分别为平行向剖面椭圆的半长轴和垂直向的剖面圆的半径.

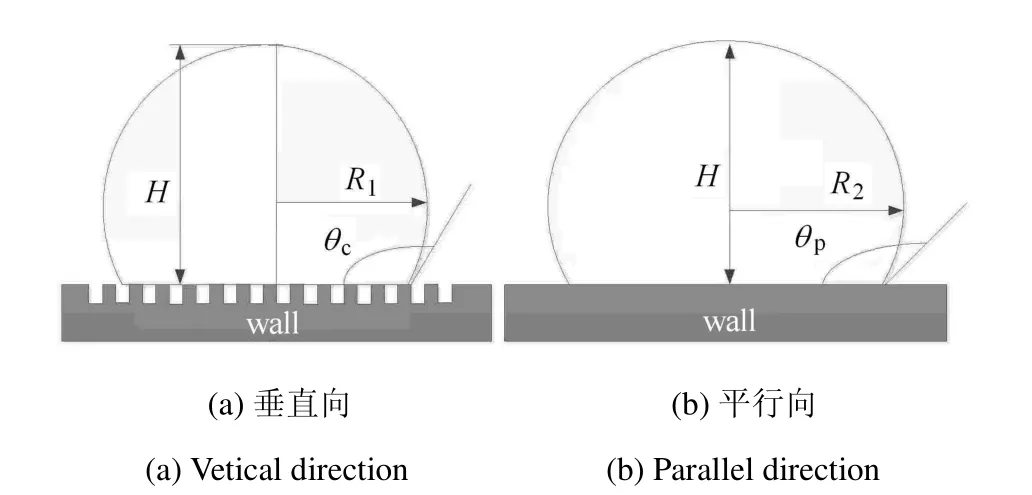
图6 矩形疏水沟槽壁面上水滴接触示意图Fig.6 Schematic diagram of water droplet on the surface of rectangular hydrophobic grooves

椭球缺体积计算公式为[32]而在垂直沟槽方向上水滴截面成球缺，所以体积V可以写为

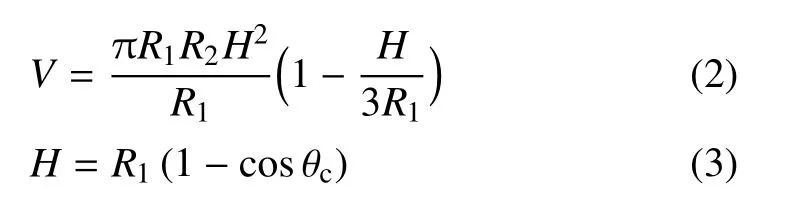
这里，θc为球缺在垂直沟槽方向上水滴的接触角，H为球缺高度.将式(3)代入式(2)中，可获得理想椭球缺的接触角、高度与体积之间的关系

同时，再代入文献[33]给出的R2与液滴滴落前球体半径之间的关系 (θp为平行沟槽方向上水滴接触角)

则可推出

由文献[34]知，固体表面上水滴的振荡周期公式为

根据矩形疏水沟槽壁面上平行向和垂直向接触角的差异性，这里假定矩形疏水沟槽壁面上水滴的振荡周期为平行垂直两方向的几何平均.式(7)给出的振荡周期公式可以修正为

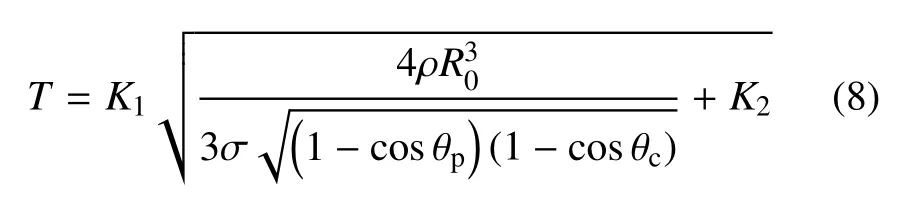
式中，K2为上述几何平均运算引入的误差修正常量.

为考察式(6)和式(8)中三角函数项的关系，这里令

并将试件θc和θp数值代入.图7为该批试验中C1和C2数值关系，其中散点为由试验数据计算获得的数值，实线为最小二乘法获得的拟合曲线，证实二者满足C2=−2.5×C1+4.4.

图7 参数C1和C2数值关系图Fig.7 Relational graph between parameter C1and C2

将C1和C2之间关系式及式(6)一起代入式(8)可得

为简化方程形式，这里取式(9)右边第一项中的常数项运算等于K3，则可表示为

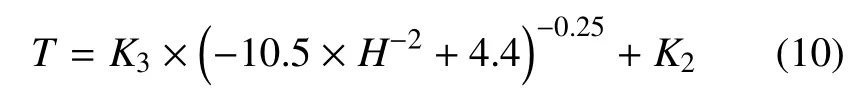
图8给出了振荡周期T与液滴最终稳定高度H的关系，其中，散点为由试验数据，实线则为用式(10)对试验数据拟合得到的曲线，二者基本吻合.由此可以初步推测，水滴高度的振荡周期确实与接触角的大小没有关系，继而与润湿性和试件表面沟槽间距无关，而仅与水滴最终稳定高度有关.

图8 振荡周期T随稳定高度H的变化曲线Fig.8 The variation of oscillating period T with stable height H

2.3 水滴三相接触线振荡

图9给出了不同撞击速度时水滴振荡过程中接触线铺展因子dc/D(dc为接触线宽度，D为液滴直径)随时间t的变化情况.其中，图 9(a)和图 9(c)为垂直沟槽方向的测量结果，图9(b)和图9(d)为平行沟槽方向上的测量结果.可以看出，在快速衰减振荡阶段，接触线的移动呈现出与水滴高度相同的振荡频率，但相位相差半个周期(高度减小时接触线外移，高度增大时接触线回缩)；但在缓慢衰减振荡过程中，接触线却基本不动.这说明疏水沟槽表面上存在的能垒束缚效应，使得水滴振荡过程中，接触线铺展和回缩运动不再服从典型阻尼振荡规律.例如，水滴以U=0.61m/s撞击后接触线经历2次振荡就可维持稳定；以U=0.44m/s撞击后接触线则经历1次振荡，但此后水滴仍会持续振荡较长时间.通过对比垂直和平行沟槽向的接触线移动曲线，还可以看出，平行沟槽方向水滴的接触线振荡持续时间明显长于其在垂直向的持续时间.

图9 水滴速度对接触线铺展因子的影响Fig.9 In fl uence of water droplet velocity on contact wire spreading factor

该过程的物理机制如下：水滴撞击壁面后发生形变，其初始动能被转化为表面能，然后又在表面张力的驱动下发生反复的变形振荡，即其动能和张力势能不断相互转移.水滴振荡期间，存在固液界面间摩擦阻力耗散和液体内部的黏性耗散作用(随水滴振荡的衰减，其能量耗散速度放缓)，致使水滴总机械能不断减小，即水滴变形振荡幅度(高度振幅和接触线移动振幅)逐渐衰减.同时，由于试件表面上存在润湿异性(实际壁面上均会呈现一定程度的各向润湿异性)导致的能垒，致使接触线能否移动取决于接触线处流体质点的能量是否克服此处的能量壁垒.在撞击后的初始振荡阶段，水滴机械能充足，其接触线会发生移动并伴随振荡；但当水滴机械能快速减小无法克服能垒后，水滴接触线不能继续移动，即接触线振荡现象消失.另外，随着水滴撞击速度的提高，水滴振荡的初始机械能增大，水滴接触线振荡持续时间延迟；同理，在能垒大的方向上，接触线振荡幅度小，且持续时间更短.

进一步观测图9还发现，撞击速度U=0.61m/s时，在槽间距l为0.2mm,0.6mm的试件上水滴会发生弹跳行为(接触线宽度能减小至0)，而槽间距l=1.0mm的试件上并未发生弹跳行为.同样，撞击速度U=0.44m/s时，只有槽间距l=0.2mm的试件上发生了弹跳行为.这说明疏水沟槽间距越小，越利于水滴发生弹跳.其原因在于：水滴撞击疏水沟槽壁面时界面一直处于Cassie润湿状态.文中疏水沟槽表面的槽宽度s和槽深度h0均相等，随槽间距l的减少，其表面固体分数不断减少，即液滴下气垫面积越大，液滴自然容易反弹.

3 结论

通过研究矩形疏水沟槽表面上水滴高度和接触线振荡行为，发现：

(1)矩形疏水沟槽表面水滴振荡过程可分为快速衰减振荡阶段和缓慢衰减振荡阶段，且前者持续时间相对短暂.

(2)矩形疏水沟槽表面的润湿异性使得振荡过程中水滴在平行沟槽方向上的接触线长度大于垂直方向；但水滴振荡周期却与沟槽间距引起的润湿性差异无关，仅是水滴最终稳定高度的函数.

(3)与水滴高度振荡行为不同，水滴三相接触线的铺展和回缩运动仅发生在撞击壁面后的初始振荡阶段(此时接触线处流体质点能量能克服能垒束缚)，且振荡相位相反，随后则不随水滴高度振荡而移动.

(4)疏水矩形沟槽的槽间距越小，水滴接触固体面积越小，即液滴下气垫面积越大，越有利于水滴发生撞击弹跳行为.

1 Hao CL,Li J,Liu Y,et al.Superhydrophobic-like tunable droplet bouncing on slippery liquid interfaces.Nature Communications,2015,6:7986

2 秦梦晓，张旭辉，汤成龙.液滴撞击不同粗糙度固体表面动力学行为实验研究.西安交通大学学报,2017,51(9):1-5(Qin Mengxiao,Zhang Xuhui,Tang Chenglong.An experimental study on the droplet impact on solid surface with di ff erent roughness.Journal of Xi’an Jiaotong University,2017,51(9):1-5(in Chinese))

3 王刚，徐守萍，皮丕辉等.液滴在梯度润湿铜表面上的定向铺展.中国科技论文,2016,11(6):659-663(WangGang,XuShouping,Pi Pihui,et al.Directional spreading of droplet on copper surface with wettability gradient.China Science Paper,2016,11(6):659-663(in Chinese))

4 朱军悦，段远源，王晓东等．流体在固体表面超铺展特性的研究进展．化工学报，2014,65(3):765-776(Zhu Junyue,Duan Yuanyuan,Wang Xiaodong,et al.Review of super-spreading of fluids on solid substrates.Journal of Chemical Industry and Engineering,2014,65(3):765-776(in Chinese))

5 于程，张程宾，陈永平等．液滴在粗糙固体表面上的铺展特性．工程热物理学报，2014，35(1):145-147(Yu Cheng,Zhang Chengbin,Chen Yongping,et al.Spreading of droplet on a rough solid surface.Journal of Engineering Thermophysics，2014，35(1):145-147(in Chinese))

6 焦云龙,刘小君,刘焜.离散型织构表面液滴的铺展及其接触线的力学特性分析.力学学报,2016,48(2):353-360(Jiao Yunlong,Liu Xiaojun,Liu Kun.Mechanical analysis of a droplet spreading on the discrete textured surfaces.Chinese Journal of Theoretical and Applied Mechanics,2016,48(2):353-360(in Chinese))

7 杨淑燕,郭峰,马冲等.固液润湿性对流体动压润滑薄膜的影响.摩擦学学报,2010,30(2):203-208(Yang Shuyan,Guo Feng,Ma Chong,et al.In fl uences of the liquid/solid wettability on thin hydrodynamic lubrication fi lms.Tribology,2010,30(2)：203-208(in Chinese))

8 Zhang HY,Li W,Fang GP.A new model for thermodynamic analysis on wetting behavior of superhydrophobic surfaces.Applied Surface Science,2012,258(7):2707-2716

9 高全杰，彭承焘，邓云峰等.雾化喷涂过程中的液滴特性研究.武汉科技大学学报(自然科学版)，2010，33(4)：417-419(Gao Quanjie,Peng Chengtao,Deng Yunfeng,et al.Characteristics of droplets during atomization and spraying process.Journal of Wuhan University of Science and Technology(Natural Science Edition),2010，33(4)：417-419(in Chinese))

10 陈石，王辉，沈胜强等.液滴振荡模型及与数值模拟的对比.物理学报,2013,62(20)(Chen Shi,Wang Hui,Shen Shengqiang,et al.The drop oscillation model and the comparison with the numerical simulations.Acta Phys Sin,2013,62(20)(in Chinese))

11 Rioboo R,Marengo M,Tropea C.Outcomes from a drop impact on solid surfaces.Atomization&Sprays,2001,11(2):155-166

12 陆军军,陈雪莉,曹显奎等.液滴撞击平板的铺展特征.化学反应工程与工艺,2007,23(6):505-511(Lu Junjun,Chen Xueli,Cao Xiankui,et al.Characteristic phenomenonan and analysis of a single liquid droplet impacting on dry surfaces.Chemical Recation Engineering and Technology,2007,23(6):505-511(in Chinese))

13 魏明锐,刘明嘉,颜伏伍等.液滴平壁铺展过程分析.内燃机学报,2012(6):538-543(Wei Mingrui,Liu Mingjia,Yan Fuwu,et al.Analysis of spreading process of droplet on fl at surface.Transactions of CSICE,2012(6):538-543(in Chinese))

14 李春曦,杨保才,叶学民.分离压对波状基底上活性剂液滴铺展过程的影响.力学学报,2015,47(1):71-81(Li Chunxi,Yang Baocai,Ye Xuemin.E ff ect of disjoining pressure on spreading of liquid droplet containing surfactant over corrugated topography surface.Chinese Journal of Theoretical and Applied Mechanics,2015,47(1):71-81(in Chinese))

15 阎凯，宁智，吕明等.圆环旋转黏性液体射流破碎液滴粒径与速度数量密度分布相关性研究.力学学报，2016,48(3):566-575(Yan Kai,Ning Zhi,LMing,et al.Study on correlation of breakup droplet size and velocity distributions of an annular swirling viscous liquid sheet.Chinese Journal of Theoretical and Applied Mechanics,2016,48(3):566-575(in Chinese))

16 赵西增,付英男,张大可等.紧致插值曲线方法在流向强迫振荡圆柱绕流中的应用.力学学报,2015,47(3):441-450(Zhao Xizeng,Fu Yingnan,Zhang Dake,et al.Application of a cip-based nu-merical simulation of flow past an in-line forced oscillating circular cylinder.Chinese Journal of Theoretical and Applied Mechanics,2015,47(3):441-450(in Chinese))

17 刘大渔，梁广铁，雷秀霞等.基于液滴技术的毛细管DNA提取//第一届国际微纳尺度生物医学分离和分析技术学术会议,上海，2010年 10月17-20日(Liu Dayu,Liang Guangtie,Lei Xiuxia,et al.DNA puri fi cation in a polytetra fl uoraethylene capillary,1st International Symposium on Micro/Nano-scale Biomedical Separation and Analysis,Shanghai,2010-10-17-20(in Chinese))

18 王飞龙,孙一宁,孙志斌等.基于PSD的静电悬浮液滴振荡技术在表面张力与黏度测量中的应用.仪表技术与传感器,2016(12):173-175(Wang Feilong,Sun Yining,Sun Zhibin,et al.Application of electrostatic levitation droplet oscillation technique in surface tension and viscosity measurement based on PSD.Instrument Technique and Sensor,2016(12):173-175(in Chinese))

19 Wang MJ,Lin FH,Ong JY,et al.Dynamic behaviors of droplet impact and spreading-water on glass and paraffin.Colloids and Surfaces a-Physicochemical and Engineering Aspects,2009,339(1-3):224-231

20 Wang MJ,Hung YL,Lin FH,et al.Dynamic behaviors of droplet impact and spreading:A universal relationship study of dimensionless wetting diameter and droplet height.Experimental Thermal and Fluid Science,2009,33(7):1112-1118

21 Banks D,Ajawara C,Sanchez R,et al.E ff ects of liquid and surface characteristics on oscillation behavior of droplets upon impact.Atomization and Sprays,2014,24(10):895-913

22 Miller CA,Scriven LE.The oscillation of a fl uid droplet immersed in anther fl uid.Journal of Fluid Mechanics,1968,32:417-435

23 Prosperetti A.Free oscillations of drops and bubbles:the initialvalue problem.Journal of Fluid Mechanics,1980,100:333-347

24 Tsamopoulos JA,Brown RA.Nonlinear oscillations of inviscid drops and bubbles.Journal of Fluid Mechanics,1983,127:519-537

25 Khismatullin DB,Nadim A.Shape oscillation of a viscoelastic drop.Physical Review E Statistical Nonlinear&Soft Matter Physics,2001,63(6Pt1):061508

26 Zhang JL,Liu QZ,Meng SJ.Numerical simulation of oscillation phenomenon for droplet spreading on solid surface by lattice Boltzmann method.Indian Journal of Physics,2016,90(5):589-594

27 Range K,Feuillebois F.In fl uence of surface roughness on liquid drop impact.Journal of Colloid and Interface Science,1998,203(1):16-30

28 Kannan R,Sivakumar D.Drop impact process on a hydrophobic grooved surface.Colloids and Surfaces a-Physicochemical and Engineering Aspects,2008,317(1-3):694-704

29 施瑶，胡海豹，黄苏和等.条纹沟槽表面润湿性的试验研究.测控技术,2011,30(11):119-121,126(Shi Yao,Hu Haibao,Huang Suhe,et al.Experimental Research on Wettability of Riblet Structure Surface.Measurement&Control Technology,2011,30(11):119-121,126(in Chinese))

30 Hu HB,Huang SH,Chen LB.Droplet impact on regular microgrooved surfaces.Chinese Physics B,2013,22(8):084702-1-084702-6

31 Song D,Song BW,Hu HB,et al.Contact angle and impinging process of droplets on partially grooved hydrophobic surfaces.Applied Thermal Engineering,2015,85:356-364

32 朱建泽.球缺、椭球缺及其实际应用.数学教学与研究,2011(29):77-78(Zhu Jianze.Ball,ellipsoid and its application.Mathematics Teaching and Research,2011(29):77-78(in Chinese))

33 黄苏和，胡海豹，陈立斌等.剪切气流驱动下微沟槽表面液滴受力分析.上海交通大学学报,2014,48(2):260-264(Huang Suhe,Hu Haibao,Chen Libin,et al.Force analysis of liquid droplets on micro-grooved surfaces with air fl ow.Journal of Shanghai Jiaotong University,2014,48(2):260-264(in Chinese))

34 Fedorchenko AI,Wang AB,Wang YH.The formation and dynamics of a blob on free and wall sheets induced by a drop impact on surfaces.Physics of Fluids,2004,16(11):3911-3920

CHARACTERISTIC OF DROPLET OSCILLATION ON THE SURFACE OF RECTANGULAR HYDROPHOBIC GROOVES1)

Dong Qiqi*Hu Haibao*,†,2)Chen Libin*Yu Sixiao*
*(College of Marine，Northwestern Polytechnical University，Xi’an710072，China)
†(Research&Development Institute in Shenzhen，Northwestern Polytechnical University，Shenzhen518057，China)

Droplet oscillation is an important phenomenon in nature,it has important scienti fi c research value.Since the liquid droplet behavior when impinging on the hydrophobic plate surface with grooved texture is obviously di ff erent from that on the smooth plate surface,the characteristics of the oscillation of the height and the contact line of water droplet on the rectangular hydrophobic grooves are studied via high-speed camera.Due to the anisotropic wetting of the rectangular hydrophobic grooves,the length of the contact line of water droplet in the parallel direction of the groove is longer than that in the vertical direction.However,it does not a ff ect the period of the attenuation oscillation in the height direction,which means the droplet oscillation period has no relationship with the width of the slot.What’s more,due to the binding e ff ect of the barrier on the surface within hydrophobic grooves,the spreading and retraction of the contact line do not follow the typical damping oscillation law.It stabilizes rapidly after several oscillations.For example,when the velocity of water droplet is 0.61m/s,the contact line is stable after 2 oscillations,but the water droplet is still oscillating.In addition,we give the reason why the water droplet oscillation period is irrelevant to the groove size.

rectangular hydrophobic grooves,water droplet,oscillation,contact line

O353.4

A doi：10.6052/0459-1879-17-225

2017–06–19 收稿，2017–08–07 录用,2017–08–11 网络版发表.

1)深圳市基础研究项目(JCYJ20160510140747996)和陕西省自然科学基础研究计划项目(2016JM1002)资助.

2)胡海豹，教授，主要研究方向：表界面力学行为机理与控制.E-mail:huhaibao@nwpu.edu.cn

董琪琪，胡海豹，陈立斌，余思潇.矩形疏水沟槽表面水滴振荡特性.力学学报,2017,49(6):1252-1259

Dong Qiqi，Hu Haibao，Chen Libin，Yu Sixiao.Characteristic of droplet oscillation on the surface of rectangular hydrophobic grooves.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1252-1259