线性规划中目标函数的变式研究

湖北省松滋市第二中学 卢 涛 (邮编：434213)

线性规划中目标函数的变式研究

湖北省松滋市第二中学 卢 涛 (邮编：434213)

通过线性规划目标函数分析,与数的形式联想图形的几何量解决问题,目的为了发展学生类比联想与解决问题的能力.

线性规划;目标函数;构造变形

线性规划是高考中的常考题型,对目标函数的分析处理形式多样,考查灵活,面对众多不同形式的目标函数类型,我们如何高效进行高三复习,本文通过一题多变,多题归一研究了目标函数的类型以期对大家复习备考有参考作用.

(1)求z＝2x＋y的取值范围.

目标函数过B(5,2)时,zmax＝12;目标函数过交点A(1,1)时,zmin＝3,故z∈ [3 ,12].

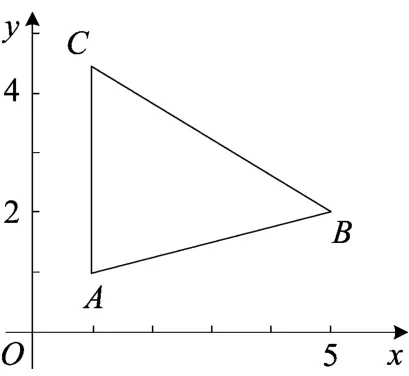
图1

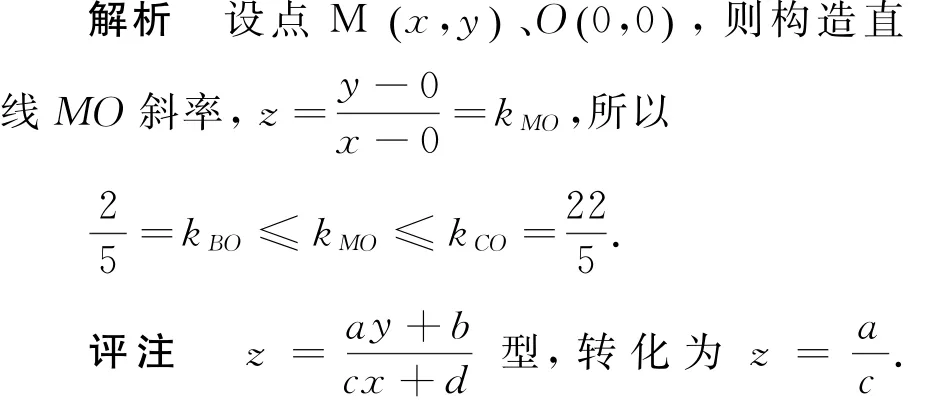
(3)设z＝x2＋y2,求z的取值范围.

解析 设点 M(x ,y)、O(0,0),构造MO两点之间的距离,MO＝,则z＝MO2,因为 AO ≤MO ≤BO,所以2≤z≤29.

评注 将目标函数转化为两点间的距离.

(4)求z＝ x＋y＋1的最小值.

解析 思路1 去掉绝对值化为x＋y＋1＝±z,求z的最小值.

思路2 构造点M(x ,y)与直线x＋y＋1＝0的距离d,则

所以z＝x＋y＋1＝ 2d,又A(1,1)到直线x＋y＋1＝0的距离d＝.

min

所以z＝2d≥3.

评注 z＝ Ax＋By＋C型转化为点M(x ,y)到直线Ax＋By＋C＝0的距离.

思路3 因为可行域在直线x＋y＋1＝0上方,所以x＋y＋1＞0,,所以z＝x＋y＋1＝x＋y＋1,故y＝－x＋z－1,得zmin＝3.

评注 应用线性规划思想直接去掉绝对值.

变式(2015高考浙江,文14) 已知实数x、y满足x2＋y2≤1,则 2x＋y－4＋6－x－3y 的最大值是 .

解析 设z＝|2x＋y－4|＋|6－x－3y|＝ －2x－y＋4＋6－x－3y＝－3x－4y＋10转化为在y轴截距形式解决.zmax＝15;

图2

思路2 满足条件的点 (x ,y)中,x＞0,y＞0,故z＝x＋2y,即y＝－,当过C1时,z＝1＋2×max＝.

评注 在题设条件下将 x的绝对值去掉,将目标函数化简求得.

(6)x＋y＝z,求z最大值.

思路1 作出 x＋y＝z的图象,若z变大时正方形DEFG逐步扩大,当正方形DEFG与△ABC相交时,当DE过B(5,2)时,zmax＝7.

评 注 将 x ＋y＝z整体考察,z相当于点D的纵坐标或者点E的横坐标.

思路2 满足条件的点 (x ,y)中,x＞0,y＞0故x＋y＝z,即y＝ －x＋z过B(5,2)时,zmax＝7.

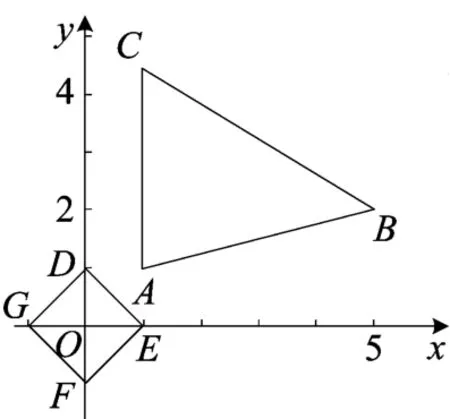
图3

评注 在题设条件下将 x 、y的绝对值去掉,将目标函数化简求得.

(7)设点P(x,y)在可行域内,点M(－2,－1)求z＝的最大值.

评注 与向量有关的借助向量计算或者几何性质解决.

变式 若P是△ABC平面区域内的一点,Q是直线2x＋y＝0上任一点,O是坐标原点,求最小值.

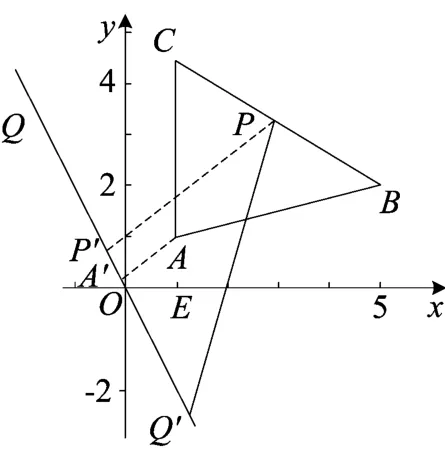
图4

(8)求xy的最大值.

解析 因为可行域内的点 x,y( )中x、y都为正值,若x一定时,要使xy最大,则要y最大.所以xy最大时点一定在线段BC上.

评注 先分析出最值可能区域,再具体求最值.

max

图5

评注 目标函数转换为与二次函数开口开阔程度的量解决.

10()若x2＋4y2≥a恒成立,则a的最大值为多少?

当椭圆过A1,1( )时椭圆的长轴最长,故amax＝12＋4×12＝5.

评注 将问题转换为椭圆的长轴的长短问题,借助椭圆几何性质解决.

思路2 设2y＝t,则问题转化为：x2＋t2≥a恒成立.

评注 通过仿射变换思想,将问题转换为熟悉的距离问题.

线性规划中目标函数主要考察数形结合,化归转化思想,考查学生分析,解决问题的能力,通过类比,联想转换成熟悉的数学模型,借助图象几何性质解决.如果我们减少题目背景,增加题目思维含量,相信在我们的复习中一定会事半功倍!

2017-09-23)