把“根”留住——含参数的零点问题的消参策略

安徽省池州市第一中学 黄立明 (邮编：247000)

把“根”留住
——含参数的零点问题的消参策略

安徽省池州市第一中学 黄立明 (邮编：247000)

有关函数的零点或极值点的问题,在高考尤其全国卷中不仅是常考的问题,而且通常是高考的压轴题,重在考查学生的数学素养、数学基本功和数学能力.设置的问题中除零点这个变量外,往往还有其它变量,解题时就是要善于消去一些变量,或者通过整体代换将多元变量化为单元变量.而在消去一些变量时,需要考虑消去哪些变量更好,更有利于问题的巧妙解决.研究发现,当极值点x0无法用参数a表示时,我们用x0表示a,并通过a的范围得到x0的范围.大多数情况下保留零点x0这个变量,即把“根”x0留住,用“根”x0表示其它变量会更方便,更有利于问题的求解.下面通过实例,探究把“根”留住的消参策略,在解决这类问题时显得更加行之有效.

1 求极值范围问题的消参策略

含参数极值范围问题是高考常考的问题,解决这类问题,通常是先根据极值点的个数求出参数的范围,然后再选择消参的策略,主要是看消去哪一个变量更容易,以及保留哪些变量更利于问题求解,从而选择最为合理的消参策略.

例1 (2009年全国卷Ⅱ)设函数f(x)＝x2＋aln(1＋x)有两个极值点x1、x2,且x1＜x2.

(Ⅰ)求a的取值范围,并讨论f(x)的单调性;

(Ⅱ)证明：f(x2)

2－2x2(1＋x2),于是f(x2)＝x22－2x2(1＋x2)ln(1＋x2).

设函数g(x)＝t2－2t(1＋t)ln(1＋t),则g′(t)＝－2(1＋2t)ln(1＋t).

评注 本题有两个极值点,由函数的定义域求得参数a的范围,再由a的范围求得“根”x2的范围,这些条件比较隐含.本题用“根”x2表示参数a,再消去参数a,保留“根”x2,解法简单.

2 极值与极值点的比值问题中的消参策略

在涉及几个极值点以及参数的时候,保留哪一个“根”最为合适,需要对问题的结构特征做出准确的判断,选择最佳的消参策略,使问题求解变得简单可行.

例2 已知函数f(x)＝x2＋aln(x＋1).

(Ⅰ)若函数y＝f(x)在区间[1,＋∞)上是单调递增函数,求实数a的取值范围;

(Ⅱ)若函数y＝f(x)有两个极值点x1、x2,且x1＜x2,求证：0

解 (Ⅰ)a的取值范围为[－4,＋∞).

因为x1＋x2＝－1,2x22＋2x2＋a＝0,

列表如下：

x (－12,x0) x0 (x0,0)p′(x) － 0 ＋

评注 本题将“根”x1和参数a都转化为“根”x2,并根据参数a的范围求出“根”x2的范围,这是最佳的消元策略,而这种消元策略不少学生可能不容易想到,他们可能认为这种消参运算量很大,很难算出结果,而恰恰这种方法是最简便的方法.解法2则利用重要不等式ln(1＋x)＜x,使问题求解简单不少,这个不等式经常会用到.

3 最值问题中的消参策略

最值问题与极值问题类似,在涉及参数的最值问题中,首先要找出最值点,通过最值点与参数的关系,既求出最值点的范围,又消去参数保留最值点,最后解决有关最值问题.

(I)讨论函数的单调性,并证明当x＞－2时,xex＋2＋x＋4＞0;

解 (1)易证,此处略.

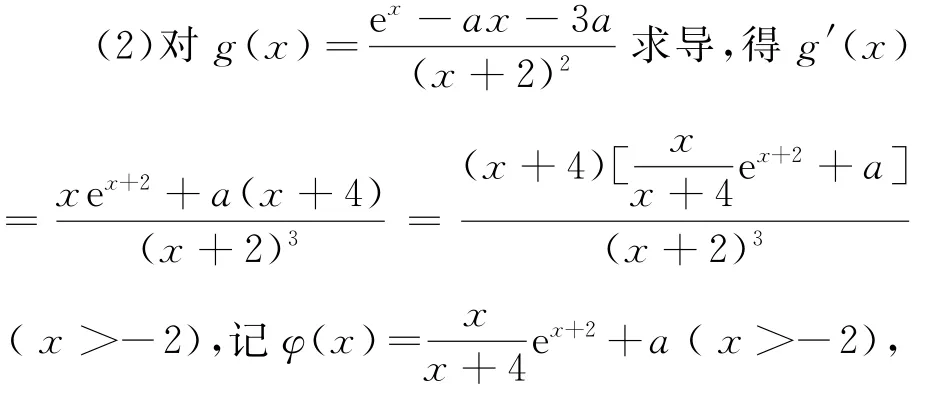
由(Ⅰ)知,函数φ(x)区间 (－2,＋∞)内单调递增,

又φ(－2)＝－1＋a＜0,φ(0)＝a≥0,所以存在唯一正实数x0,－2＜x0＜0,使得

于是,当x∈ (－2,x0)时,φ(x)＜0,g′(x)＜0,函数g(x)在区间(－2,x0)内单调递减;

当x∈(x0,＋∞)时,φ(x)＞0,g′(x)＞0,函数g(x)在区间(x0,＋∞)内单调递增.

所以g(x)在(－2,＋∞)内有最小值g(x0)

所以u(－2)＜u(x)≤u(0),

评注 本题求解需要层层深入,先求出最小值,用参数a及“根”x0两个变量表示最小值(x0不是题目给的,而是虚设的一个变量.),根据零点存在定理求出“根”x0的范围,消去参数a,保留“根”x0,使问题顺利求解.

4 含多个参变量问题的消参策略

有些问题中含有多个参变量,消去哪些变量和保留哪些变量对解题繁简程度有很大影响,所以需要对式子的结构特征做出准确判断,选择最佳的消参策略,使问题求解朝着简单的方向努力.

A.－e3B.－e2C.－e D.－

因为f(x)存在极小值,所以方程－x2＋bx＋a＝0有两个不等正根,

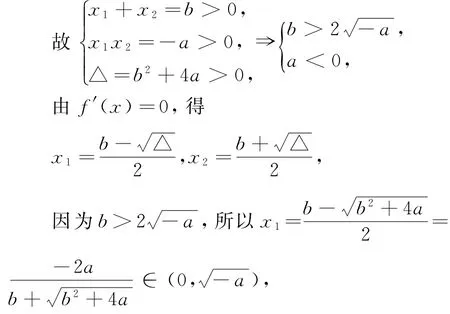
易知f(x)在 (0,x1)递减,在 (x1,x2)递增,在(x2,＋∞)递减.

则f(x)极小值恒大于0,等价于g(x)恒大于0,

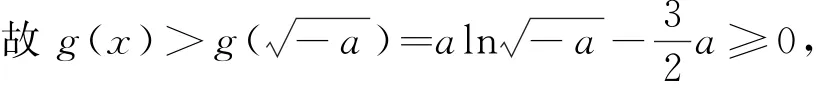
解得a≥－e3,故amin＝－e3,选A.

评注 本题是2016年安徽省江南十校的一道考试题,学生普遍感到这道题比较难,这道题的综合性比较强.通过存在极小值这个条件,求出参数a、b的范围,进而求出极小值点x1的范围.极小值点x1是虚设的,保留“根”x1,且将变量b换成变量a,这是问题求解的巧妙之处!

例5 (2009年全国卷I)设函数f(x)＝x3＋3bx2＋3cx在两个极值点x1、x2,且x1∈[－1,0],x2∈ [1,2].

(I)求b、c满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点 (b,c)的区域;

2

解 (I)此处从略;

(II)证明：由题意有f′(x2)＝3x22＋6bx2＋3c＝0 ①

又f(x2)＝3x32＋3bx22＋3cx2②

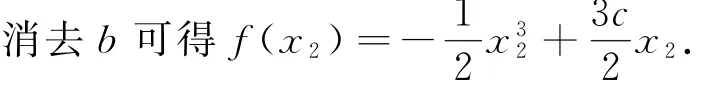
又x2∈[1,2],且c∈[－2,0],所以

评注 (I)这一问主要考查了二次函数根的分布及线性规划作可行域的能力.大部分考生有思路并能够得分.

(II)这一问考生不易得分,有一定的区分度.主要原因是含字母较多,不易找到突破口.此题主要利用消元的手段,消去目标f(x2)＝x32＋3bx22＋3cx2中的b,(如果消c会较繁琐)再利用“根”x2的范围,并借助(I)中的约束条件得c∈[－2,0]进而求解,有较强的技巧性.

5 综合性问题中的消参策略

综合性问题中要考虑的条件较多,有些条件单从表面上看比较复杂,需要我们看清式子的结构特征,挖掘隐含条件,将式子化简变形,找出它们之间的简洁关系,便于消去一些变量,使问题求解朝着简捷的方向进行.

例6 (2015年四川卷)已知函数f(x)＝－2(x＋a)lnx＋x2－2ax－2a2＋a,其中a＞0,(I)设g(x)是f(x)的导函数,讨论函数g(x)的单调性

(Ⅱ)证明：存在a∈(0,1)使得f(x)≥0在区间(1,＋∞)内恒成立,且f(x)＝0在区间(1,＋∞)内有唯一解.

(2)证法1 由(1)得f′(x)＝g(x)在(1 ,＋∞)内单调递增,且

f′(1)＝－2－2a＋2－2a＝－4a＜0,f′(＋ ∞)＞0.由零点存在性定理得存在唯一x0∈ (1 ,＋∞)(虚设零点x0)使得

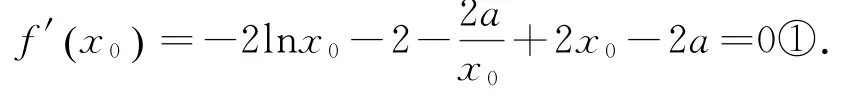
f(x)在(1,x0)上单调递减,(x0,＋∞)上单调递增.

所以满足f(x)＝0在区间 (1 ,＋∞)内有唯一解只需满足f(x)min＝f(x0)＝0即可.

f(x0)＝－2(x0＋a)lnx0＋x20－2ax0－2a2＋a＝0,将①带入消去lnx0化简得：

2a2＋ (5x0－2x20)a－(x30－2x20)＝0(以a为主元,便于因式分解)

(2 a －x0)(a＋x20－2x0)＝0,

所以h(x)在 (1 ,2)上单调递减.h(x)＜h(1)＝－2＜0不满足.

当a＝2x0－x20时(用“根”x0表示参数a,巧妙!),此时①变形为2x20－2lnx0－6＝0在(1 ,2)上有解.

不妨设h(x0)＝2x20－2lnx0－6,h′(x0)＝

所以h(x0)在 1,2( )上单调递增.h(1)＝－4＜0,h2()＝2－2ln2＞0,所以2x20－2lnx0－6＝0在 1,2( )上有解.所以命题得证.

证法2 由证法1得

我们的目标是证明这个二元方程组有实数解,且至少有一组解满足限制条件x0＞1且0＜a＜1.采用消元的策略,由第一个方程与第二个方程作差,整理得(x0＋2a)(a＋lnx0－1)＝0,因此a＝1－lnx0(用“根”x0表示参数a,巧妙!),代入－x0lnx0＋x20－(a＋1)x0－a＝0可得x20－2x0－1＋lnx0＝0,容易判断出x0∈(1,e),因此对应的a∈(0,1),命题得证.

因此函数g(x)的最小值为－2lnx0－2x20＋4x0＋2＝0,从而可以估计出x0∈(1,e),因此对应的a∈(0,1),命题得证.

评注 由于所得的初始条件比较复杂,需要对初始条件进行化简变形,这有较强的技巧.证法1化简后得到的式子是：a＝,a＝2x0－x20,

证法2化简后得到的式子是：a＝1－lnx0,证法1和证法2不是简单粗暴的代入消元,而是注意到联立方程组,通过代数变形大大简化a与x0的关系,实施精准打击.证法3转化原来的复杂函数,通过一次求导得到极值点,并通过化简得到简洁的式子：a＝x20－2x0,然后利用与主思路一致的方式解决问题.三种证法的共性都是用“根”x0表示参数a,体现了在消参中把“根”留住的消参策略.

例7 已知a为常数,f(x)＝x－a·ex有两个零点x1、x2,求证：x1＋x2＞2.

121＜1,x2＞1,x1＝a·ex1,x2＝a·ex2,

x1－x2＝a(ex1－ex2),x1＋x2＝a(ex1＋(用“根”x1、x2表示参数a),

要证x1＋x2＞2,即证a(ex1＋ex2)＞2,

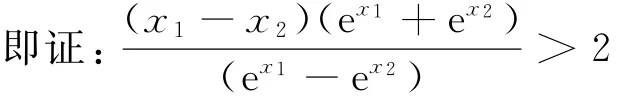
(消去参数a保留“根”更简便),

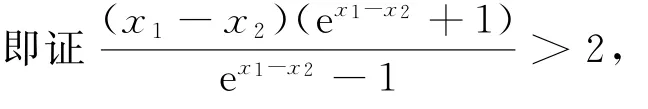
令x1－x2＝t,则t＜0,即证(将多元变量化成单元变量),

即证(t－2)et＋t＋2＜0.

令φ(t)＝(t－2)et＋t＋2(t＜0),则φ′(t)＝et＋(t－2)et＋1＝(t－1)et＋1,

φ″(t)＝et＋(t－1)et＝tet＜0(因t＜0),

则φ′(t)在 (－∞,0)递减,φ′(t)＞φ′(0)＝0,得φ(t)在(－∞,0)递增,即φ(t)＜φ(0)＝0,结合可知,φ(t)＜0,命题得证.

评注 (1)用“根”表示参数a简便易行;(2)多元变量化成单元变量使问题化繁为简,化难为易;(3)本题还可以用极值点偏移的方法先证：x1＋x2＞－2lna(－lna为函数f(x)的极值点),因为0＜a＜,所以－2lna＞2,所以x＋x12＞2,命题得证.

转化与化归思想是数学中最重要的数学方法,可以说在数学解题中无处不在.转化与化归思想就是化繁为简,化难为易,化生为熟,化未知为已知.我们在数学解题中经常发现,一个小小的变形(如移项、分式化整式、加一项再减一项、式子两边同乘以2等),往往会带来意想不到的效果,使问题求解变得十分简便,给人带来美的享受和思维的启迪.把“根”留住,就是较好地体现了转化与化归的思想,将其它参数转化到“根”上来,这是解决与“根”有关问题的最佳策略,而且具有通性.在课堂教学中,教师要善于引导学生探求问题的内在规律,发现解决问题的“巧思妙解”,激发学习数学的兴趣,培养创新精神,提高数学素养.

2017-10-17)