基于改进最小二乘的缺陷椭圆定位方法∗

何志强 曹 彪 张立新

（海军航空工程学院基础实验部 烟台 264001）

基于改进最小二乘的缺陷椭圆定位方法∗

何志强 曹 彪 张立新

（海军航空工程学院基础实验部 烟台 264001）

分析形心法、Hough变换法和最小二乘拟合法等典型椭圆中心提取算法在应用中对噪声过于敏感、抗干扰性差的不足，提出了一种基于随机抽样一致性方法的改进最小二乘椭圆中心提取算法，经过仿真实验分析表明，该算法与最小二乘法、形心法相比具有更高的定位精度和强鲁棒性。

中心定位；椭圆拟合；最小二乘法；RANSAC

1 引言

在基于视觉的航天器交汇对接中，物体位姿定和摄像机的参数标定等是通过图像中一系列特征点坐标计算得到［1］。圆形标志相对其他形状，以噪声抑制性强、便于识别和提取而得到广泛使用。但是在相机成像过程中，圆形标志经过透视投影变换后，在图像中呈现椭圆的形状。所以对椭圆中心坐标准确提取是相机标定、位姿测量等应用中至关重要的环节，其中心坐标提取的准确性直接影响了最终计算结果的精度。因此，准确提取椭圆中心坐标有着重要意义。

目前常见椭圆中心定位算法有重心法、形心法、Hough变换法、高斯曲面拟合法和最小二乘拟合法等［2］。形心法是一种内部区域表示法，以特征标志外形为特征。首先进行图像分割，然后进行图像二值化，在提取到二值图像椭圆轮廓后，在轮廓区域内使用形心法提取椭圆中心。重心法则可以看成是以灰度为权值的加权形心法，在灰度图像中将轮廓区域内各点灰度值作为权值进行加权平均计算。不管是形心法还是重心法，都是对椭圆轮廓区域进行处理，对区域内噪音敏感。Hough变换法是利用图像空间上的椭圆与参数空间点之间的对偶性，满足通过该点的超平面数目最多即认为改点的坐标值就是椭圆参数值，Hough变化虽然具有较强的鲁棒性，但随着模型参数增加计算量和存储量指数增加，无法满足现代检测对实时性的要求。高斯曲面拟合法则假设椭圆的灰度分布满足二维高斯分布特征［3］，在此基础上用二维高斯曲面来拟合椭圆标志，对于不能简化为点光源的模型该假设一般不能成立。最小二乘法属于曲线拟合算法，提取椭圆轮廓后将轮廓像素点坐标带入参数方程通过最小化误差平方和来找到一组最佳匹配参数［4～5］。所以这些方法都要求特征椭圆轮廓是完整的，当椭圆轮廓存在干扰信号尤其是当椭圆轮廓残缺不全时会严重影响拟合精度。但是在实际采集椭圆图像过程中由于环境光照、振动等非控制量因素影响会导致图片中存在大量噪音，严重影响拟合精度，严重时甚至会直接导致拟合结果失效，所以考虑在椭圆拟合时如何在包含有误差的数据集中最大程度的得到准确的参数模型是本文研究的问题。

随机抽样一致性（Random sample consensus，RANSAC）方法是基于已知参数模型来判别数据点是否为有效数据［6～8］，RANSAC算法属于强鲁棒性算法，可以容忍超过半数的离群数据，大量理论和实际应用说明该方法可以有效解决上述问题［9］。本文分析比较了形心法、最小二乘拟合法等典型椭圆中心提取算法在应用中对噪声敏感，抗干扰性差的不足等问题，故本文根据RANSAC算法的强鲁棒性特点，提出了一种基于RANSAC的缺陷椭圆中心提取算法，经过仿真实验分析表明，该算法能够保持椭圆中心提取精度同时还具有很强的鲁棒性。

2 基本概念和算法模型

2.1 最小二乘法椭圆模型

如图1中所示，平面上任一椭圆可以由椭圆长轴b短轴a，中心坐标(xc，yc)和长半轴与轴夹角θ共5个独立参数来唯一确定［10］。则椭圆方程可以表示为：

图1 椭圆方程

令式（3）取得最小值为约束条件，则有：

由式（4）有

将式（5）写成矩阵形式表示为

则式（6）可变为

参数向量X可由下式解出

2.2 基于RANSAC改进最小二乘算法

RANSAC算法主要根据随机表决的原理，来计算模型参数［11～12］。

令参数向量 X=(A，B，C，D，E)，d 为拟合误差范围，u为阈值，N为最大迭代次数。图2所示为算法流程图。

本文算法步骤如下：

1）随机抽取一组观测样本数据t，本文中抽取8个数据点以保证一定的亢余。

2）将样本数据带入本文式（8）中，得到参数方程解X。

3）计算所有数据点与 X的拟合残差delta（i），记录残差绝对值小于d的样本数目，记为K1。由多次实验确定文中d=4时可以取得较好拟合效果。

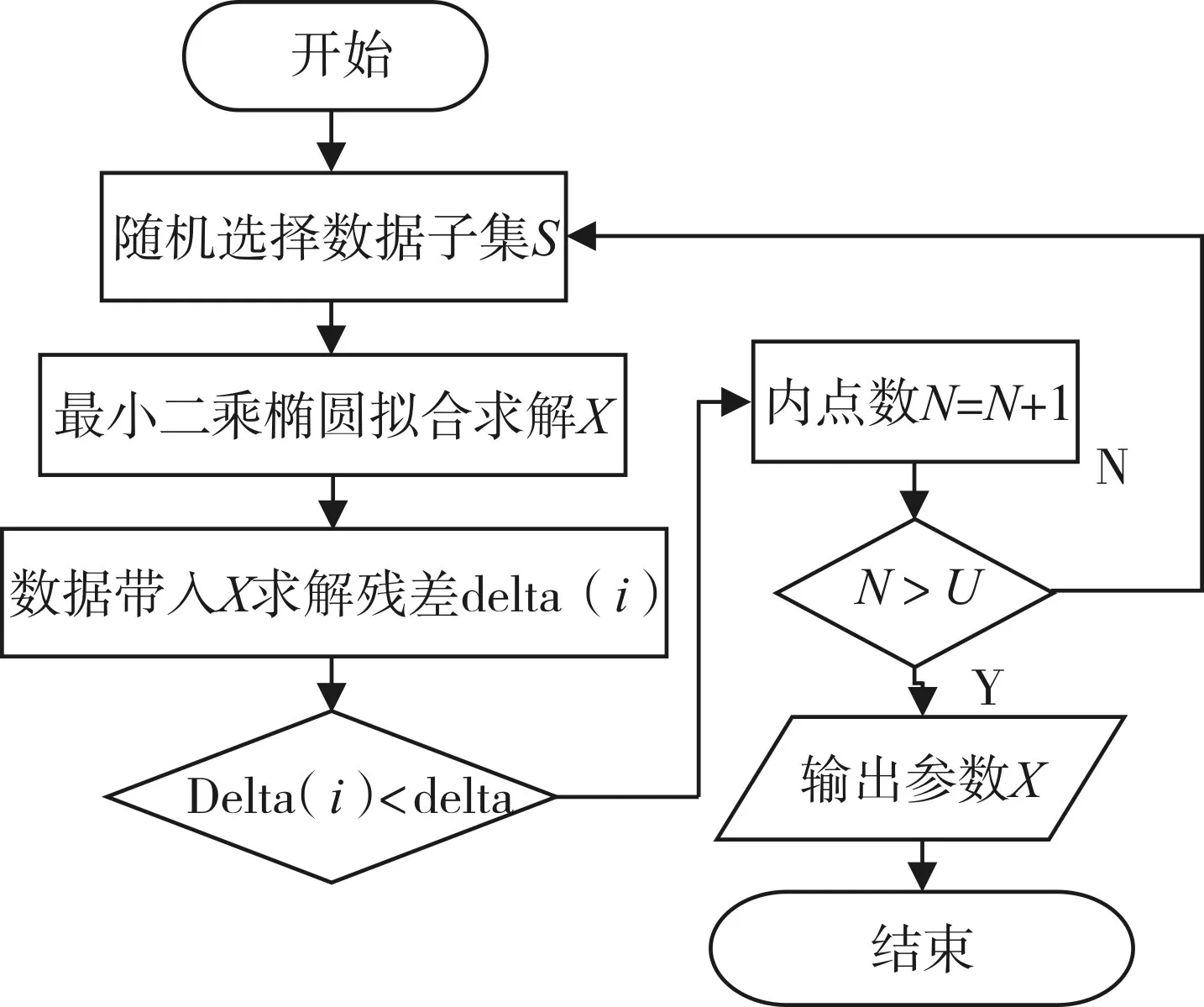
图2 算法流程图

4）重复以上步骤N次，得到K1K2…KN，取N=100。其中N根据参考文献12中估计式估计得到。

5）取 K=max{K1K2…KN}对应的参数方程解Xj，j∈(1，2…N)即为求得最优解。

3 仿真实验及分析

目前没有表征椭圆缺陷变形的一般的为验证算法是否有效，首先用计算机生成中心坐标已知的不同形状椭圆并在椭圆中加入不同类型的缺陷，如轮廓缺失、轮廓突出、边缘不平整等［13～15］。如图3所示，所有椭圆的理想中心坐标已知，椭圆1为无缺陷的理想椭圆，椭圆2～椭圆5为含有一种缺陷的椭圆，椭圆6、7、8为含有两种或以上缺陷的椭圆图像。对图3中椭圆图片分别使用形心法、最小二乘法和本文算法来提取椭圆中心坐标，得到表1。

图3 仿真椭圆图像

表1 椭圆中心坐标

将各算法提取的中心定位坐标与标准值相减并取绝对值得到各算法绝对误差的绝对值为σ，并分别用σ1、σ2和σ3表示形心法、最小二乘法和本文算法的绝对误差。图像上任一像素点P的综合像素误差应该满足以下公式：

根据表1中数据整理可得到误差数据表2和误差分布图4。

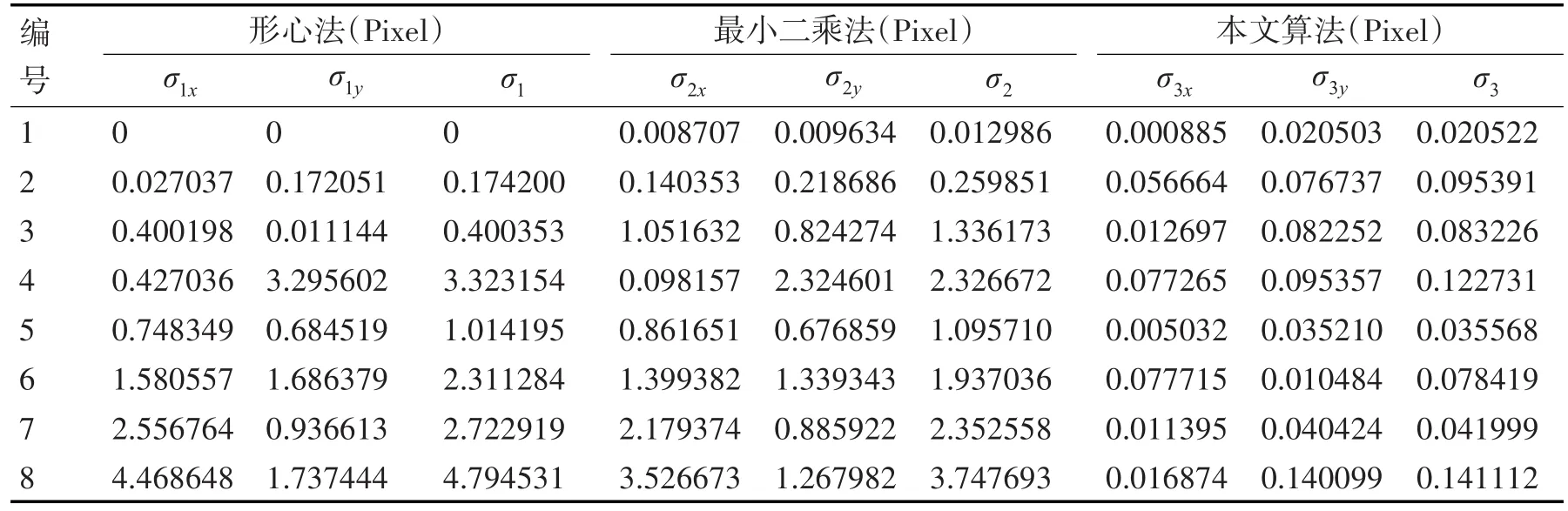
表2 绝对误差数据

由图4可以看出，在理想椭圆图形中本文算法和形心法及最小二乘法具有同数量级的定位精度。在缺陷椭圆图形中，本文算法定位误差略有变大但不超过0.15个像素，而形心法和最小二乘法的定位误差随缺陷不同而有较大变化。最大定位误差出现在图3中的8号椭圆中，形心法和最小二乘法的定位误差分别是4.8像素、3.7像素，对应的本文算法定位误差小于0.14像素，具有亚像素级定位精度且定位结果不随椭圆缺陷的不同而变化，具有较好的鲁棒性。

图4 绝对误差分布

4 结语

对椭圆中心定位算法研究分析发现主要算法都存在抗干扰性不足的问题，提出了一种基于随机约束一致性的改进最小二乘法算法，仿真实验结果分析表明该算法定位精度可达到亚像素级并且还具有一定鲁棒性。

［1］吴亮，王智灵.一种新的基于椭圆模型的鲁棒估计方法［J］.数据采集与处理，2010，25（3）：407-412.WU Liang，WANG Zhiling.A new robust estimation method based on elliptic model［J］.Data acquisition and processing，2010，25（3）：407-412.

［2］周红锋，任朴生.光学测量中光斑图像的处理及测量精度研究［J］.鸡西大学学报，2014，14（5）：61-63.ZHOU Hongfeng，REN Chengsheng.Study on the processing and measurement accuracy of spot image in optical measurement［J］.Journal of Jixi University，2014，14（5）：61-63.

［3］陈天飞，赵吉宾.基于射影变换圆阵靶标中心像点的计算［J］.仪器仪表学报，2015，36（4）：895-900.CHEN Tianfei，ZHAO Jibin.The projective transformation of circular array target center image point calculation based on［J］.Chinese Journal of scientific instrument，2015，36（4）：895-900.

［4］Fitzgibbon A，Pilu M，Fisher R B.Direct least square fitting of ellipse［J］.Pattern Analysis and Machine Intelligence，1999，21（5）：476-480.

［5］林润芝，杨学友，邹剑，等.面向大尺寸检测CCD图像中心提取精度的研究［J］.传感器与微系统，2010，29（12）：51-53.LIN Runzhi，YANG Xueyou，ZOU Jian，et al.Research on the extraction accuracy of CCD image center for large size measurement［J］.Sensors and Microsystems，2010，29（12）：51-53.

［6］高晶，吴育峰，吴昆，等.基于角点检测的图像匹配算法［J］.仪器仪表学报，2013，34（8）：1717-1724.GAO Jing，WU Yufeng，WU Kun，et al.Image matching algorithm based on corner detection［J］.Chinese Journal of scientific instrument，2013，34（8）：1717-1724.

［7］张丽敏，朱枫，郝颖明，等.基于圆特征和异面点特征的位姿测量［J］.光子学报，2015，44（11）：20021-20025.ZHANG Limin，ZHU Feng，HAO Yingming，et al.Pose measurement based on circular features and different point features［J］.Journal of photonics，2015，44（11）：20021-20025.

［8］尹玄武，王贵锦，施陈博，等.基于RANSAC和灰度一致性的PET瓶胚口缺陷检测［J］.计算机应用研究，2012，29（9）：3525-3527.YIN Xuanwu，WANG Guijin，SHI Shi，et al.Detection of PET bottle mouth defects based on RANSAC and gray level coherence［J］.Computer Application Research，2012，29（9）：3525-3527.

［9］张虎，达飞鹏，邢德奎.光学测量中椭圆圆心定位算法研究［J］.应用光学，2008，29（6）：905-911.ZHANG Hu，DA Feipeng，XING Dekui.Optical measurement of ellipse center location algorithm of［J］.Applied Optics，2008，29（6）：905-911.

［10］解则晓，顾宾.一种圆形标记点的快速提取算法［J］.光学技术，2013，39（5）：393-397.XIE Zexiao，GU Bing.Rapid extraction algorithm［J］.Optical Technology of a Circular Marker，2013，39（5）：393-397.

［11］李江涛，倪国强，王强，等.一种快速准确识别圆形目标的新算法［J］.激光与红外，2007，3（6）：575-578.LI Jiangtao，NI Guoqiang，WANG Qiang，et al.A new algorithm for fast and accurate identification of circular targets［J］.Laser and Infrared，2007，3（6）：575-578.

［12］王军华，李丁，刘胜鹏.基于改进RANSAC的消防机器人双目障碍检测［J］.计算机工程与应用，2017，53（2）：236-240.WANG Junhua，LI Ding，LIU Shengpeng.Improved RANSAC estimation based fire-fighting robot obstacle detection using binocular vision［J］.Computer engineering and application，2017，53（2）：236-240.

［13］安新源，周宗潭，胡德文.椭圆拟合的非线性最小二乘方法［J］.计算机工程与应用，2009，45（18）：188-190.Xin an source，ZHOU Zongtan，HU Dewen.Nonlinear least square method for ellipse fitting［J］.Computer Engineering and Applications，2009，45（18）：188-190.

［14］谭燕，邹峥嵘.近景摄影测量圆形标志与其椭圆构像的 中 心 偏 差 估 计［J］.测 绘 科 学 ，2009，34（6）：250-251.TAN Yan，ZOU Zhengrong.Estimation of the central deviation of circular symbols and their ellipses in close range photogrammetry［J］.Journal of Surveying and Mapping Science，2009，34（6）：250-251.

［15］张广军，魏振忠.结构光三维视觉检测中光条椭圆中心定位方法与仿真研究［J］.仪器仪表学报，2003，24（6）：589-593.ZHANG Guangjun，WEI Zhenzhong.Research on the method and Simulation of light strip ellipse center positioning in structured light 3D vision inspection［J］.Chinese Journal of scientific instrument，2003，24（6）：589-593.

A Defect Ellipse Locating Method Based on Least Squares

HE ZhiqiangCAO BiaoZHANG Lixin
（Department of Basic Science，Naval Aeronautical and Astronautical University，Yantai 264001）

In this paper，an improved elliptic ellipse center extraction algorithm based on stochastic sampling consistency method is proposed，which is too sensitive to noise and has poor anti-jamming performance in typical ellipse center extraction algorithms such as centroid method，Hough transform method and least squares fitting method.Simulation results show that the proposed algorithm has higher accuracy and strong robustness compared with the least square method and the centroid method.

central location，ellipse fitting，least square method，RANSAC

TP242.6

10.3969/j.issn.1672-9722.2017.11.007

Class Number TP242.6

2017年5月12日，

2017年6月29日

何志强，男，硕士研究生，助理工程师，研究方向：机器视觉、模式识别、虚拟现实。