基于多重频脉冲串信号解速度模糊的研究

夏梦颖 苏卫民 顾 红 卢建春



基于多重频脉冲串信号解速度模糊的研究

夏梦颖①苏卫民*①顾 红①卢建春②

①(南京理工大学电子工程与光电技术学院 南京 210094)②(94647部队 福州 350000)

针对双重频解速度模糊系统中，信号参数选择不合理导致解速度模糊存在量化误差的问题，推导了双重频解速度模糊的量化要求。为了增大最大不模糊速度，该文提出多层解模糊系统，提出了一种四重频脉冲串解速度模糊的模型，推导了四重频信号脉冲个数的下界，并简化为了三重频脉冲串信号模型。仿真验证了理论推导的正确性。

多重频雷达；解速度模糊；量化要求；1维集算法

1 引言

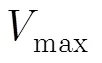
在多重频解速度模糊系统中，如何选取合适的重频数、脉冲重复周期和脉冲个数，使能解模糊的速度范围尽量大并且解速度模糊没有量化误差成了本文的研究方向。在雷达的距离分辨率和目标最高速度确定的条件下，目标最高速度跨过一个距离分辨单元的时间确定，对于高速目标，则雷达允许对目标的最大积累相干时间有限，需要选取合适的信号参数以满足测距测速要求。本文将通过推导，计算脉冲重复数的下界，使在双重频测速范围内，解速度模糊时不会出现二义性。提出了一种四重频脉冲串解速度模糊的新方式，可以获得更大的速度不模糊范围，并根据双重频脉冲串信号解速度模糊的量化要求，推导出四重频信号脉冲个数的下界，随后简化了四重频脉冲串信号为三重频脉冲串信号。

2 问题模型

解模糊实际上是多维有限空间的点到1维有限空间点的信号映射。由数据选取和数据处理的特点决定了速度解模糊算法有别于距离解模糊算法。在距离解模糊算法中，多维有限空间中每一维空间的数据个数不一样，各维空间数据的采样间隔一样，此时可以按中国余数定理求解距离模糊。速度模糊求解算法所遇到的情况正好相反，多维有限空间中各维空间的数据个数一样，而数据之间的采样间隔不一样。这就决定了速度解模糊算法有别于距离解模糊算法，中国余数定理只能有条件地应用[11]。

解模糊算法要求多维有限空间和1维有限空间的点是一一对应的。速度模糊的实际形成过程是1维有限空间到多维有限空间的变换，解模糊只不过是其逆过程变换而已。因而在所确定的最大范围内，要求多维有限空间映射到1维有限空间的点不会出现二义性。由于频率域各维空间有不同的量化间隔，当采样个数较小时，在中国余数定理所确定的最大不模糊频率范围内，保证不了多维有限空间的点到1维有限空间的点不会出现二义性，那么就会出现由于量化误差造成的解速度模糊误差。

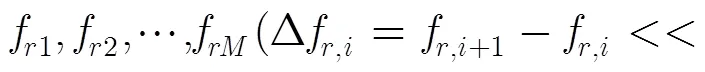
3 解速度模糊量化要求理论推导

3.1 双重频速度量化要求理论推导

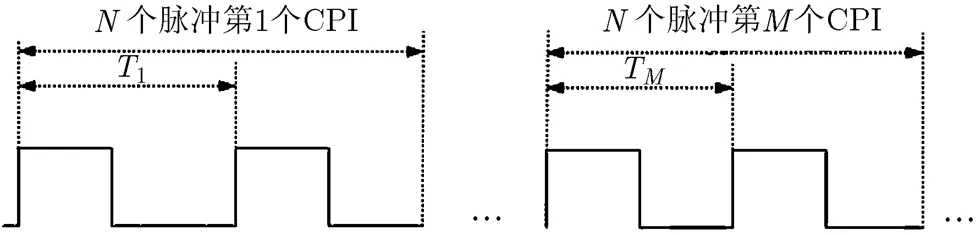
图1 多重频雷达发射信号波形(重频数为M)

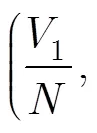
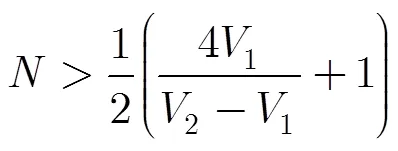
3.2 当脉冲个数不同时双重频速度量化要求理论推导

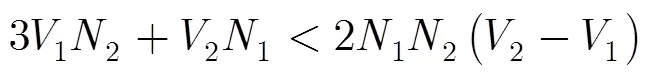
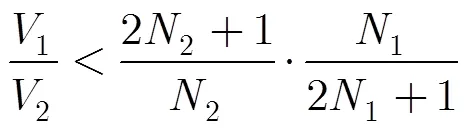
为简化模型，下文中均假设每种CPI的脉冲个数相同且均为。

3.3 多层解模糊模型建立和速度量化要求理论推导

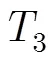
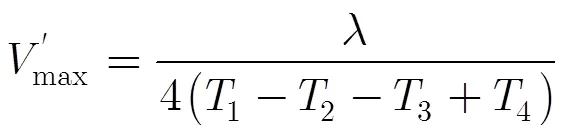
在选取合适的参数条件下，利用四重频解速度模糊将会获得比双重频更大的不模糊测速范围。由双重频解速度模糊的量化要求可推得四重频解速度模糊的量化要求为

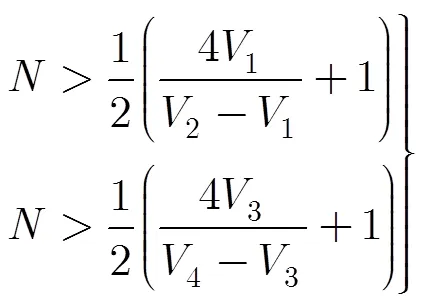
图2为多层解速度模糊时最大测量速度的二叉树。

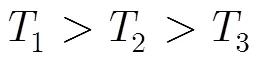
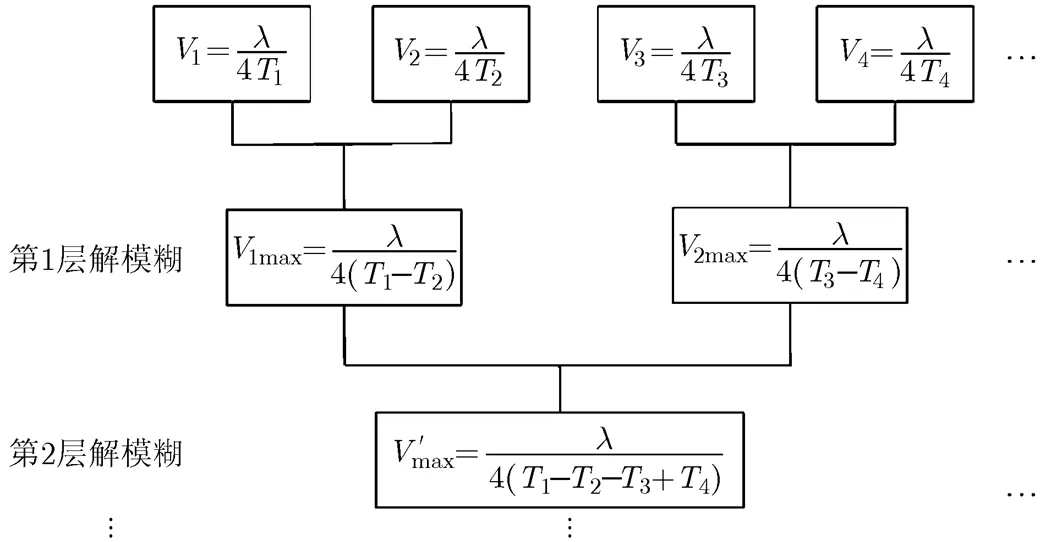
图2 多层解速度模糊时最大测量速度的二叉树

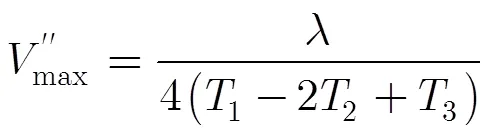
三重频由于精简了一重频，则需要两次使用中间重频的测速结果。由双重频解速度模糊的量化要求可推得三重频解速度模糊的量化要求为

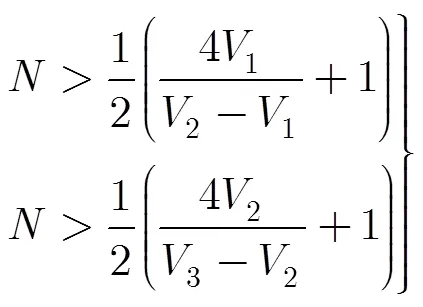
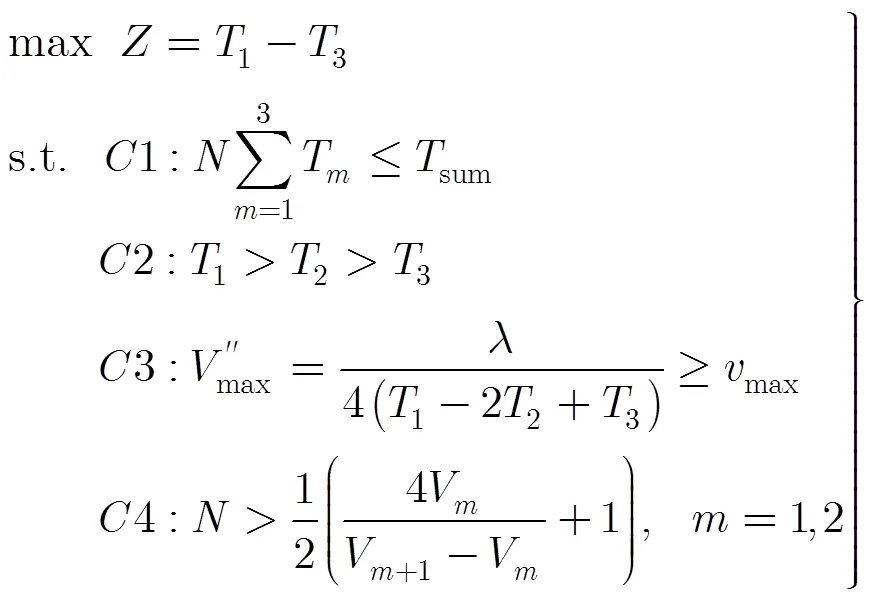
4 仿真及结果分析

仿真1 解速度模糊的量化误差

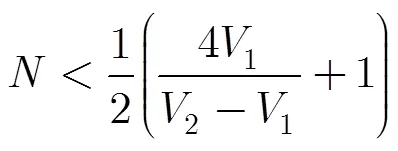
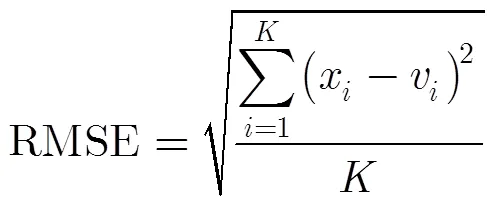
仿真2 三重频两层解速度模糊效果

5 结束语

针对多重频解速度模糊系统中，信号参数选择不合理导致解速度模糊存在量化误差或解模糊的速度范围不够大的问题，本文通过推导，计算了脉冲重复数的下界，使在双重频测速范围内，当脉冲个数相同或不同时，解速度模糊时不会出现二义性。提出了一种四重频脉冲串解速度模糊的新方式，并推导了四重频信号脉冲个数的下界，简化了四重频脉冲串信号为三重频脉冲串信号。因为本文都是在信噪比足够大的场合下进行计算的，理论推导时假设不存在速度门测量错误的情况，而实际测量中，采用多层多重频脉冲串信号解速度模糊时，若存在速度门测量误差或有量化误差的情况，则对最终速度的测量可能存在较大影响。该算法的鲁棒性研究将是下一步研究方向。

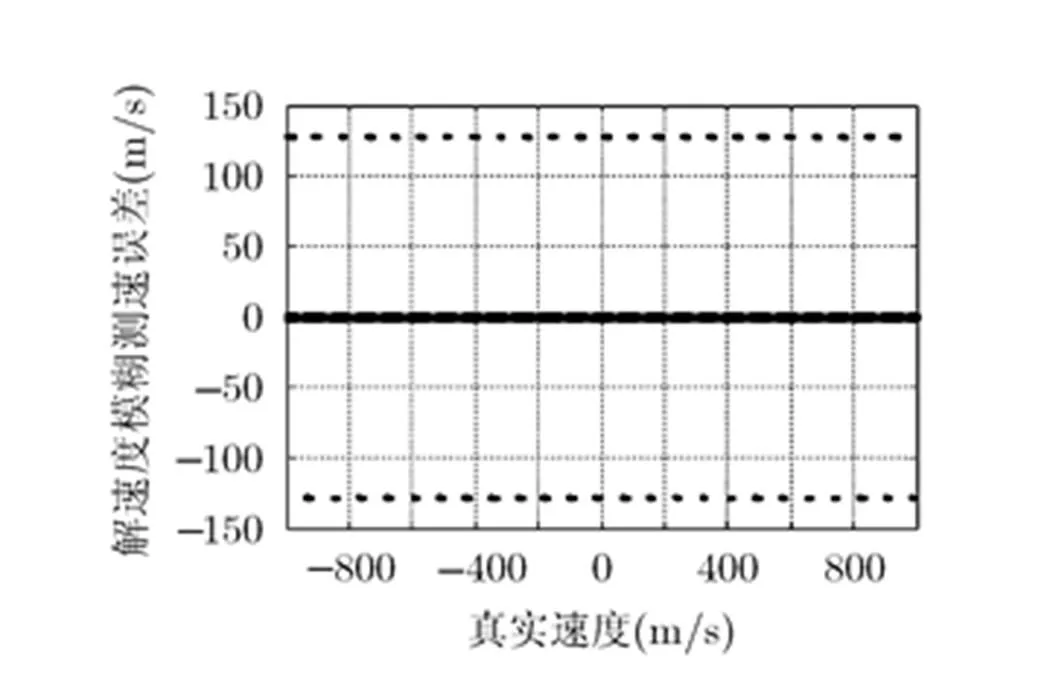
图3 存在量化误差时1维集解速度模糊测速误差图

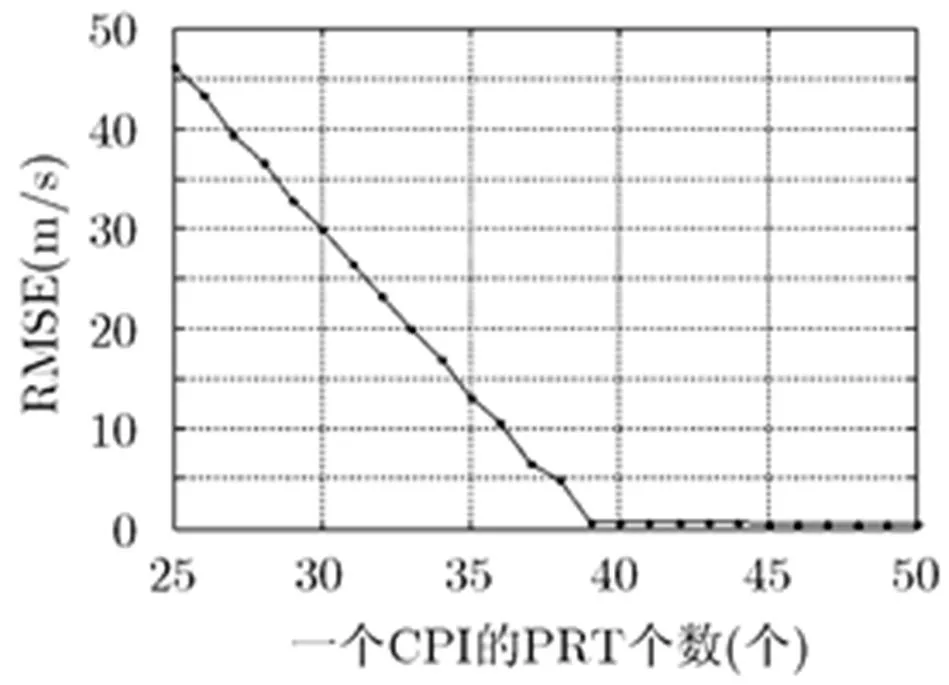
图4 不同PRT个数与1维集解速度模糊均方根误差曲线

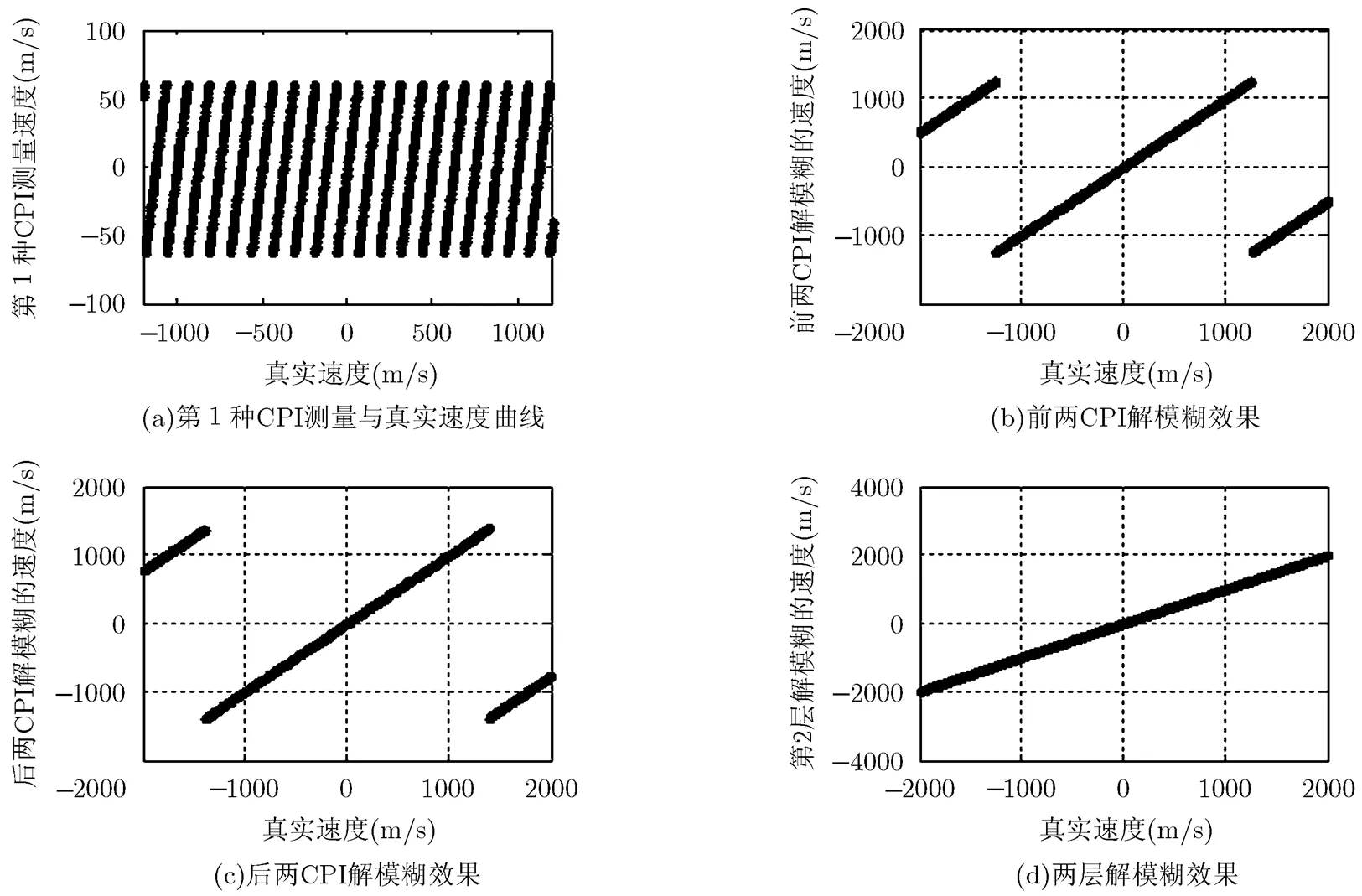
图5 多层解速度模糊效果

[1] DOVIAK R J and ZRNIC D S. Doppler Radar and Weather Observation[M]. New York: Academic, 1993.

[2] WANG Zhirui, XU Jia, and HUANG Zuzhen. Doppler ambiguity resolver via range blur in range-Doppler domain[J]., 2016, 52(20): 1719-1721. doi: 10.1049/el. 2016.1000.

[3] HOVANESSIAN S A. Medium PRF performance analysis[J]., 1982, 18(3): 286-296. doi: 10.1109/TAES.1982.313320.

[4] CHANG C Y and CURLANDER J C. Application of the multiple PRF technique to resolve Doppler centroid estimation ambiguity for spaceborne SAR[J]., 1992, 30(5): 941-949. doi: 10.1109/36.175329.

[5] 黄振兴, 万征. 距离-速度噪扰数据同时分辨的孙子定理算法[J]. 电子学报, 1992, 20(9): 27-33.

HUANG Zhenxing and WAN Zheng. Simultaneous ambiguity resolution on noisy range and velocity data via CRT algorithm[J]., 1992, 20(9): 27-33.

[6] 秦国栋, 陈伯孝, 陈多芳, 等. 多载频MIMO雷达解速度模糊及综合处理方法[J]. 电子与信息学报, 2009, 31(7): 1696-1700. doi: 10.3724/SP.J.1146.2008.01054.

QIN Guodong, CHEN Baixiao, CHEN Duofang,Velocity ambiguity resolution and synthesis processing in multi-frequency MIMO radar[J].&, 2009, 31(7): 1696-1700. doi: 10.3724/SP.J.1146.2008.01054.

[7] XU Jingwei, LIAO Guisheng, ZHANG Yuhong,An adaptive range-angle-Doppler processing approach for FDA- MIMO radar using three-dimensional localization[J]., 2017, 11(2): 309-320. doi: 10.1109/JSTSP.2016.2615269.

[8] 陈春晖, 张群, 罗迎, 等. 一种步进频率信号认知雷达波形优化设计方法[J]. 航空学报, 2016, 37(7): 2276-2285. doi: 10.7527/S1000-6893.2016.0063.

CHEN Chunhui, ZHANG Qun, LUO Ying,A waveform optimization designing method for cognitive radar with stepped-frequency signal[J]., 2016, 37(7): 2276-2285. doi: 10.7527/S1000-6893. 2016.0063.

[9] TRUNK G and BROCKETT S. Range and velocity ambiguity resolution[C]. Proceedings of the IEEE National Radar Conference, New York, 1993: 146-149.

[10] SUN J, TIAN J, and WAND G. Doppler ambiguity resolution for multiple PRF radar using iterative adaptive approach[J]., 2010, 46(23): 1562-1563. doi: 10.1049/el. 2010.1865.

[11] 洪一. 脉冲多普勒雷达的速度模糊求解[J].现代电子, 1995, 50(1): 19-22.

HONG Yi. Resolution on velocity for pulse Doppler radar[J]., 1995, 50(1): 19-22.

[12] ZRNIC D S and MAHAPATRA P. Two methods of ambiguity resolution in Pulse Doppler weather radars[J]., 1985, AES-21(4): 470-483. doi: 10.1109/TAES.1985.310635.

[13] TAHANOUT M, El Hamid Adane Abd, and CHATELET Jacques Parent du. An improved M-PRT technique for spectral analysis of weather radar observations[J]., 2015, 53(10): 5572-5582. doi: 10.1109/TGRS.2015.2425549.

[14] SI Hongwei and LI Zhaohui. An optimization design scheme for multiple PRT and multi-frequency coherent Doppler velometry[C]. 2016 MTS/IEEE OCEANS’16 Conference, Shanghai, 2016: 1-6.

[15] XIA Mengying, SU Weimin, and GU Hong. The research on Doppler ambiguity for dual pulse repetition frequencies radar[C]. CIE International Conference on Radar, Guangzhou, 2016: 1090-1093.

夏梦颖： 女，1990年生，博士生，研究方向为阵列信号处理.

苏卫民： 男，1959年生，教授，博士生导师，主要研究方向为阵列信号处理、雷达成像.

顾 红： 男，1967年生，教授，博士生导师，主要研究方向为雷达信号处理、噪声雷达体制、稀疏阵列信号处理.

卢建春： 男，1983年生，助理工程师，研究方向为阵列信号处理、信息自动化.

Research on Velocity Ambiguity Resolution for Multiple PRF Radar

XIA Mengying①SU Weimin①GU Hong①LU Jianchun②

①(,,210094,)②(94647,350000,)

In dual pulse repetition frequencies radar systems, mathematical deduction of the number of pulse repetition intervals required to satisfy quantitative requirements is presented to resolve velocity ambiguity. Multiple layer systems to increase the maximum unambiguous velocity are proposed. A new model of quadruple pulse repetition frequencies signal is proposed. The lower bound of the number of pulse repetition intervals required to satisfy quantitative requirements is deduced and quadruple pulse repetition frequencies signal is simplified as triplet pulse repetition frequencies signal. Simulation results validate the accuracy of our deduction.

Multiple pulse repetition frequencies radar; Resolving velocity ambiguity; Quantitative requirements; Clustering algorithm

TN958

A

1009-5896(2017)12-2860-06

10.11999/JEIT170259

2017-03-29；

2017-09-21；

2017-11-01

通信作者：苏卫民 suweiminnust@163.com

国家自然科学基金(61471198)

The National Natural Science Foundation of China (61471198)