面向时间同步业务的空间信息网络拓扑聚合图模型

蔚保国 鲍亚川 魏海涛



面向时间同步业务的空间信息网络拓扑聚合图模型

蔚保国 鲍亚川*魏海涛

(卫星导航系统与装备技术国家重点实验室 石家庄 050081)(中国电子科技集团公司第五十四研究所 石家庄 050081)

空间信息网络的发展呈现出节点异构和功能多样化趋势，网络节点间的时间同步是实现协同任务的重要技术基础。论文对空间信息网络的时间同步业务特性进行了分析，并提出基于多跳中继的时间同步误差模型。针对非实时时间同步业务特点，提出了钟差相对不变性概念，并基于此提出了面向时间同步业务的空间信息网络拓扑聚合图模型。不同于面向通信业务的网络拓扑模型，该模型的建立以节点时钟性能和时间比对链路性能为约束条件，反映了时间同步业务的特性和需求。针对该模型进行了空间信息网络时间同步仿真实验，实验结果表明基于该模型进行多跳中继时间同步，可以减少时间同步过程的路由筛选及建链次数，降低时间同步业务的链路资源消耗，同时可以达到更高的时间同步精度。

空间信息网络；时间同步；钟差相对不变性；拓扑聚合图

1 引言

空间信息网络是以地球同步卫星(GEO和IGSO)、中轨道卫星(MEO)、低轨道卫星(LEO)、平流层气球和有人或无人驾驶飞机等空间平台为载体，实时获取、传输和处理空间信息的网络系统[1]。最初的空间信息网络是基于星间链路由空间平台作为节点所构建的网络，主要面向解决空间平台的信息传输问题，服务于卫星通信系统，最典型代表是1998年部署的铱星系统。随着星间/星地链路技术的逐渐成熟，多类非卫星通信系统包括GPS、北斗、GRACE、“白云”系列监视卫星系统等也采用星间链路技术实现了节点间信息的互传以及高精度测量，执行自主导航、空间物理实验以及多星协同目标监视等功能。

面向未来的空间信息网络发展，美国于2004年提出了TSAT计划[2,3]，计划在太空建立类似地面的Internet网络，把太空、空中、陆地、海洋的网络整合为一体化；欧洲提出了全球通信一体化空间架构(ISICOM)，计划基于微波和激光链路构建大容量空间信息网络，将包括通信卫星、伽利略导航卫星系统、对地观测卫星星座、高空平台、无人机以及地面网络融为一体[4]。我国也在谋划开展天地一体化信息网络的设计论证[5,6]。

未来空间信息网络的发展呈现出节点数量剧增、节点类型异构以及功能业务多样化的趋势，而节点间的功能协同将成为空间信息网络重要的应用模式。时间同步，作为网络运行以及节点协同的基础，是实现空间信息网络大时空跨度网络体系结构，动态网络环境下的高速信息传输，稀疏观测数据的连续反演与高时效应用等技术的重要保障，在未来的空间信息网络体系架构中具有关键作用。

目前针对空间信息网络拓扑模型的研究主要面向通信业务，为了表征空间信息网络的动态拓扑特征，空间信息网络时变图模型被提出[7]，在此基础上又有学者提出了扩展时变图等模型，针对空间信息网络空间连接、传输和计算等多维能力评估方法进行了探索[8]。在网络模型研究的基础上针对空间信息网络的信息容量理论[9]、资源管理方法[10,11]和最大流路由算法[12]等研究成果不断涌现。这些研究绝大多数都面向通信业务，以实现通信容量与服务质量最优化为目标，但是对于空间信息网络时间同步，这些模型没用反映时间同步业务的本质特点和需求，难以满足时间同步业务性能最优化的需求。

本文面向空间信息网络时间同步需求，基于对空间信息网络时间同步业务特性的分析，提出了空间信息网络的钟差相对不变性以及时间比对误差模型，在此基础上提出了基于钟差相对不变性的空间信息网络拓扑聚合图模型，并进行了空间信息网络建模仿真与时间比对实验，实验表明基于该模型进行空间信息网络时间同步可以以更少的比对建链次数获得更优的时间同步性能。

2 空间信息网络时间同步误差模型

目前的GPS和北斗系统均基于星间链路建立了星间测量通信网络，采用双向时间同步体制实现星地和星间的时间同步，当进行时间同步的两节点的时间信号传播路径及设备处理时延绝对对称时，理论上可以消除所有系统误差，因此双向时间同步是目前精度最高的时间同步技术之一，时间同步精度最高可达亚纳秒级，是未来空间信息网络时间同步的主要技术体制之一，本文将以此作为研究对象。

空间信息网络条件下的节点数量庞大且分布广泛，可视节点间可以通过单一双向链路直接实现时间同步，但是大量节点间不具备可视条件或者比对链路作用距离有限，这类节点间的时间同步将需要依赖于一个或者多个节点作为中继实现彼此间的双向时间同步。根据中继节点类型的不同，可以分为透明转发双向时间同步，以及中继比对多跳双向时间同步两种类型。

透明转发中继时间同步过程中，中继节点不进行时间比对的处理，只进行时间同步信号的转发，一般中继节点只有一个，目前广泛应用的地面站间双向时间同步就是这一类型的典型代表，如图1(a)所示。由中继节点引入的误差主要是转发时延不等误差。其误差模型为

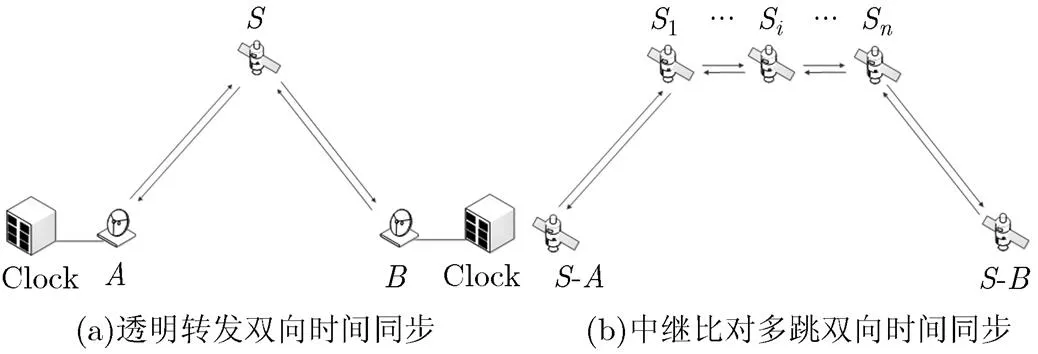
图1 空间信息网络条件下的中继双向时间同步

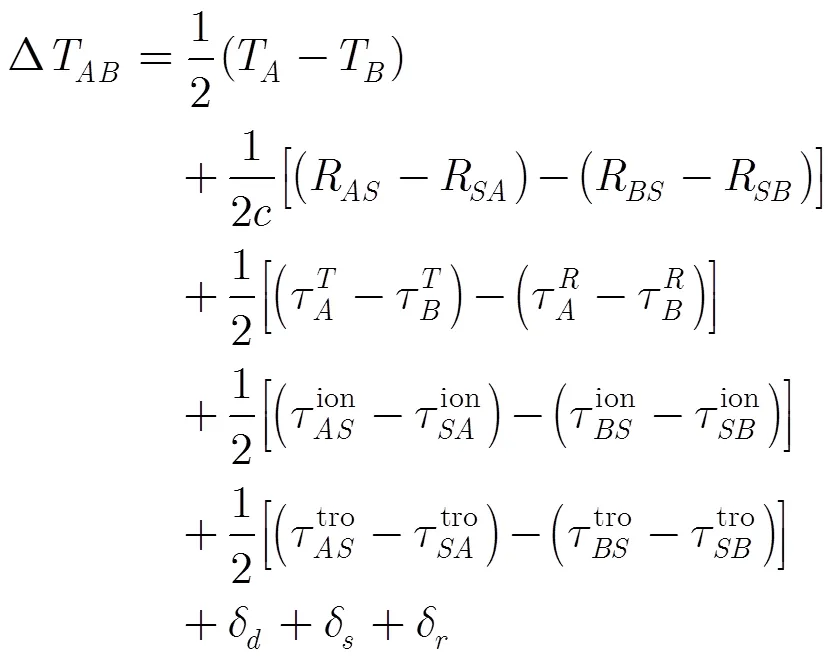
对于中继比对多跳双向时间同步，中继节点不进行时间同步信号的转发，而是作为时间同步过程的直接参与者，进行钟差的处理与解算。这种模式下，/钟差等于整个链路所包含+1次双向时间比对钟差之和。

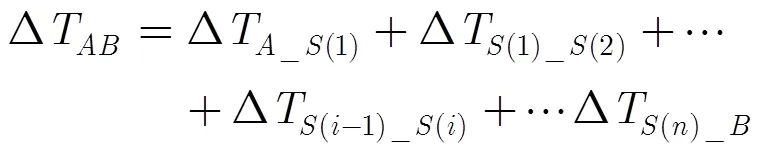
时间同步误差也就等于每条中继链路的时间同步误差为各种影响误差的累积。发起的时间同步两节点的时间同步误差等于整条比对链路中各单链路的时间比对误差的累积，此外还会受到比对过程中各中继节点原子钟的钟差漂移影响。

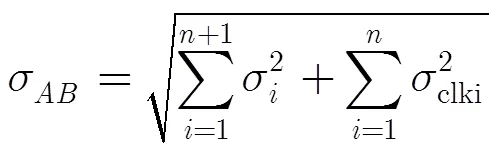
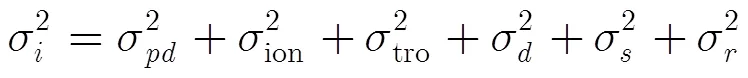
归纳来说，基于中继节点的双向时间比对性能会受到各中继链路比对精度的影响，同时也会受到中继节点时频性能的影响。若中继节点原子钟稳定性能很差，在短时间内就会发生较为明显的时钟偏差，由此将导致比对结果的不准确。

3 空间信息网络时间同步业务特性分析

空间信息网络节点间时间同步业务，根据其应用时效性可以分为实时性和非实时性两类。

实时性业务主要面向一些不具有较好守时能力的节点，要保持时间同步需要提高时间同步的频度，强调钟差信息的实时获取；非实时业务，一种是装备高稳定原子钟的节点间时间同步，同步过程允许较长时延的存在，典型代表是欧空局空间原子钟计划(ACES)中类似于空间搬钟法的非共视时间同 步[13]；另一种是面向事后数据处理的时间同步信息业务，时间比对信息不应用于节点间时间同步，而用于观测数据后期融合处理、事后精密钟差产品生成、精密轨道外推等。总体而言，空间原子钟技术的进步使非实时的时间同步业务在空间信息网络中应用更为广泛。

对于非实时的时间同步业务，高精度测量是其根本目标，少量的较高精度测量相比于多次较低精度的测量平均对于提高整体测量精度更有意义，结合其比对过程的间歇性和延迟性特点，因此在时间比对链路的选择上，可以在时间和空间尺度上进行综合考虑。

3.1 钟差相对不变性

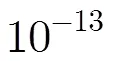
如式(2)所示，对基于多点中继的时间同步，中继节点具有较好的频率准确度，其在一定时间间隔内钟差的变化相对于时间比对测量精度而言是可以忽略的话，可以认为是该中继节点的钟差相对不变。

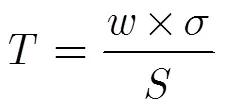
不同频率准确度和比对测量精度条件下的钟差相对不变时间如表1所示。

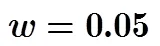
50025050 50002500500 50000250005000

3.2 等效钟差相对不变性

高准确度的原子钟可以具有很长的钟差相对不变时间，但是空间信息网络中大量的节点往往只能装备性能有限的原子钟，因此其钟差相对不变时间有限。从另一个角度来说，如果能够对节点原子钟的钟差在一段时间内进行精确预报，在该时段内，以该节点作为中继节点进行双向时间同步，基于精确钟差预报对时间比对结果进行补偿，理论上也可以消除中继过程时延所带来的误差。

钟差预报与原子钟准确度、星座建模方法以及预报算法等有关。空间原子钟的精密钟差建模与预报技术目前主要应用于卫星导航定位领域，可以分为短期预报和长期预报两类。短期预报主要面向高精度定位应用，长期预报主要面向现代化卫星导航系统的自主导航需求。常用的钟差预报模型主要有多项式模型、周期项模型、灰色模型以及ARIMA模型等[14]。相关研究表明针对导航卫星的精密钟差预报精度可以达到2小时内误差约为0.1~0.2 ns[14,15]。

基于上述分析可将精确钟差预报时间定义为等效钟差相对不变时间，

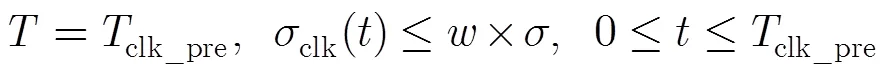
4 基于钟差相对不变性的空间信息网络拓扑聚合图

4.1 空间信息网络时变拓扑

由于卫星的运动特性，空间信息网络具有时变性特征，其网络拓扑也就具有了典型的时变特征以及断续连通特征。在不同时段，空间信息网络节点连通情况不断改变，在每一个时段的网络拓扑图，被称为快照图，快照图变化具有周期性。

拓扑快照图也可以用拓扑矩阵进行表示。矩阵元素定义如下：

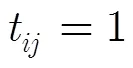
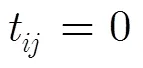
以图2中网络拓扑为例，网络内共用7个节点，网络拓扑可表示为7×7拓扑矩阵。不同时段节点连通性不同，将获得不同的网络拓扑矩阵。时段1的拓扑矩阵为

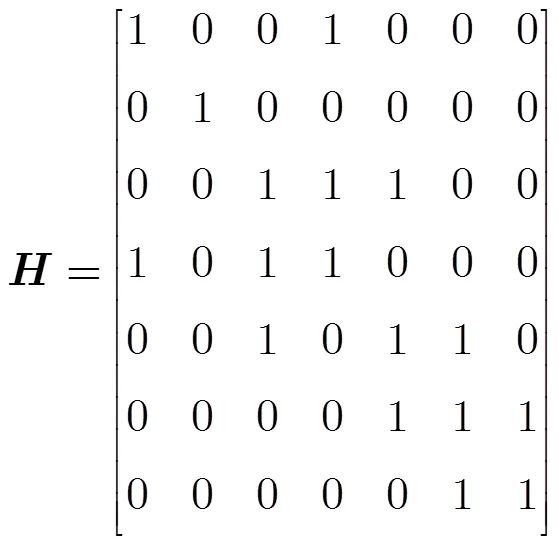
4.2 基于钟差相对不变性的空间信息网络拓扑聚合图

基于时间比对节点的钟差相对不变性，提出了空间信息网络时间比对拓扑聚合图模型。该模型基本思想是将钟差相对不变时间间隔内的空间信息网络拓扑时变图进行聚合，形成拓扑聚合图。基本原理如图3所示。

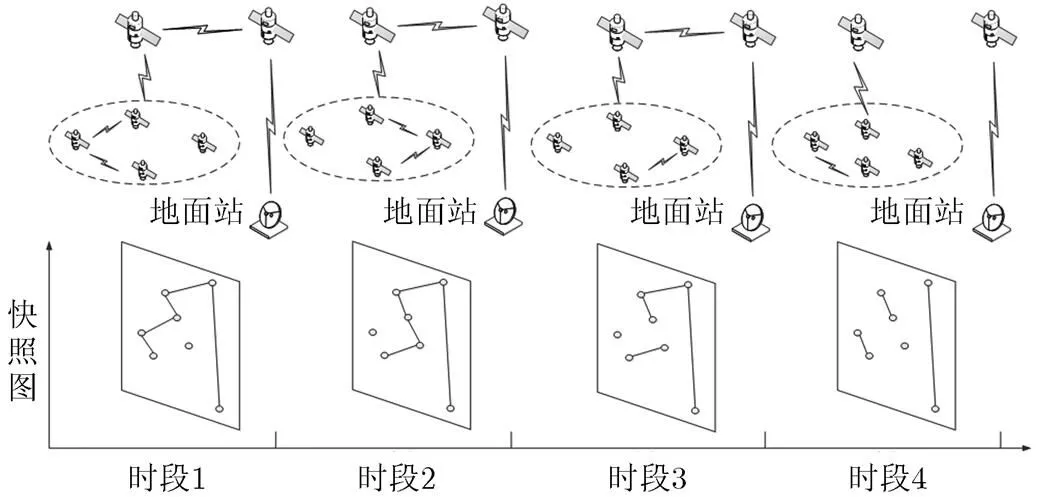
图2 空间信息网络拓扑时变图

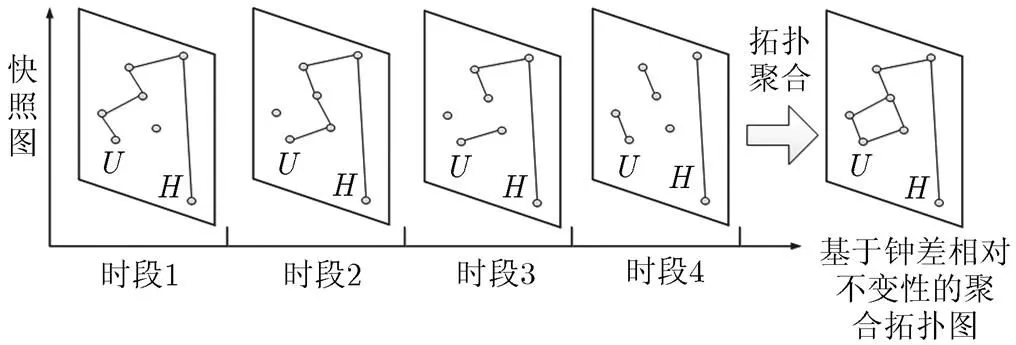
图3 基于钟差相对不变性的空间信息网络拓扑聚合图

空间信息网络内的时间同步基本要素由时间比对节点和比对链路构成。比对节点根据时间过程中的功能可以划分为端节点和中继节点。

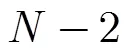
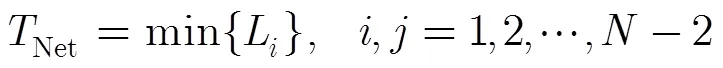
网络拓扑具有时间起点差异性，在不同的起始时刻发起时间比对，会形成不同的拓扑聚合图。拓扑聚合图变化周期只与中继节点寿命有关，与端节点寿命无关。

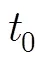
基于钟差相对不变性的拓扑聚合图网络模型进行空间信息网络节点间时间比对链路规划，相比基于聚合前的空间网络时变图模型可以带来以下的优势：反映了时间比对网络的特点，基于非实时时间同步业务特点实现了对不同时段拓扑的连通，可以获得更优的多点中继时间比对性能；减少网络拓扑图的数量，减少拓扑搜索次数。

4.3 基于拓扑聚合图的多跳时间同步方法

基于所提出的时间比对网络拓扑聚合图模型以及多跳时间同步误差模型，算法主要解决中继多跳时间同步方法中中继节点的优化选择问题，算法主要包括以下3个步骤。

(1)空间信息网络拓扑聚合图生成：根据网络内中继节点的原子钟性能或钟差预报水平确定各节点钟差不变时间，确定拓扑聚合图更新周期，根据网络拓扑快照图叠加得到基于网络拓扑聚合图。

(2)比对链路代价定义：以各中继节点间的比对链路时间同步测量精度作为链路选择的主要约束条件，各条比对链路的时间同步精度通过长期观测得到，以此作为链路选择的代价。

(3)比对链路优选：基于代价最小原则进行比对链路优选，每个拓扑聚合图周期进行一次链路优选。可选用Dijkstra或者Floyd代价最小算法进行链路的选取。

4.4 模型性能分析

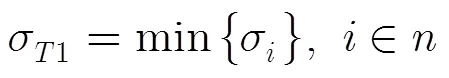
式中，假设该时段包含条比对路径。

设拓扑聚合周期包含个时段。在该周期内基于时变图模型得到时间同步误差均方根为

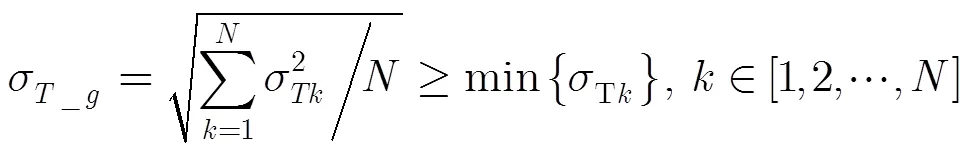
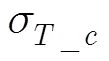
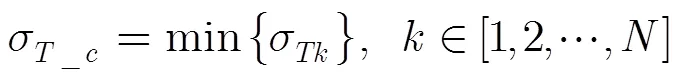
基于拓扑聚合模型所获得的时间同步误差上限与基于时变图模型的时间同步误差下限一致，因此基于拓扑聚合可以使得多跳中继时间同步获得更好的时间同步精度。

5 基于拓扑聚合图的空间信息网络时间同步仿真实验

5.1 空间信息网络建模

基于STK进行空间信息网络建模，该网络包含一个地面站，一颗LEO卫星，2颗GEO卫星，以及3 颗MEO卫星。如图4所示。地面站选取为北京，LEO卫星采用天宫2号轨道数据，两颗GEO卫星分别位于东经80°和东经140°, 3颗MEO卫星为同轨道面Walker星座，轨道高度为27906.1 km。卫星间均可以建立双向时间比对链路进行时间同步。

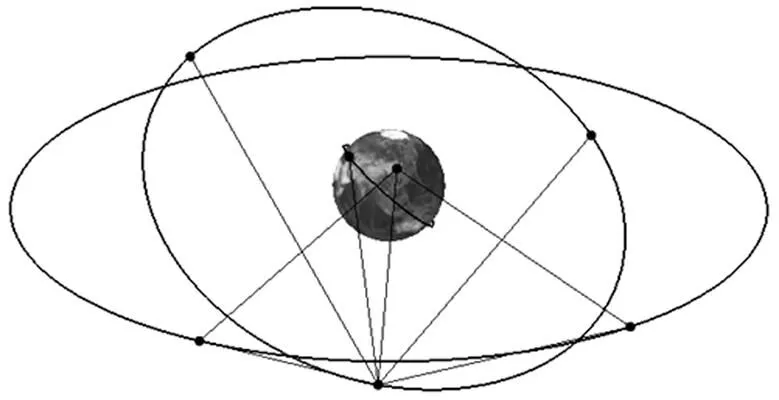
图4 空间信息网络轨道星座图

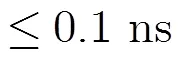
表2各节点原子钟参数

原子钟秒稳钟差预报时间钟差不变时间(最低1 ns比对测量精度，w 取为0.1) 地面站- 天宫2- MEO12 h内0.1 ns2 h MEO22 h内0.1 ns2 h MEO32 h内0.1 ns2 h GEO12 h内0.1 ns2 h GEO22 h内0.1 ns2 h

5.2 时间同步实验

取2016年12月5日至2016年12月6日24小时运行时段进行观测实验，以MEO3与地面站的时间比对过程进行实验。该时间段内地面站及MEO3与其他各节点的链路连通性如图5所示。时变图快照频度为30 min。网络拓扑聚合图周期为2 h，截取21:00~23:00时段进行分析。

该时段内的网络时变拓扑矩阵如下，矩阵元素顺序按照地面站、天宫二号、MEO1, MEO2, MEO3, GEO1和GEO2的顺序排列。

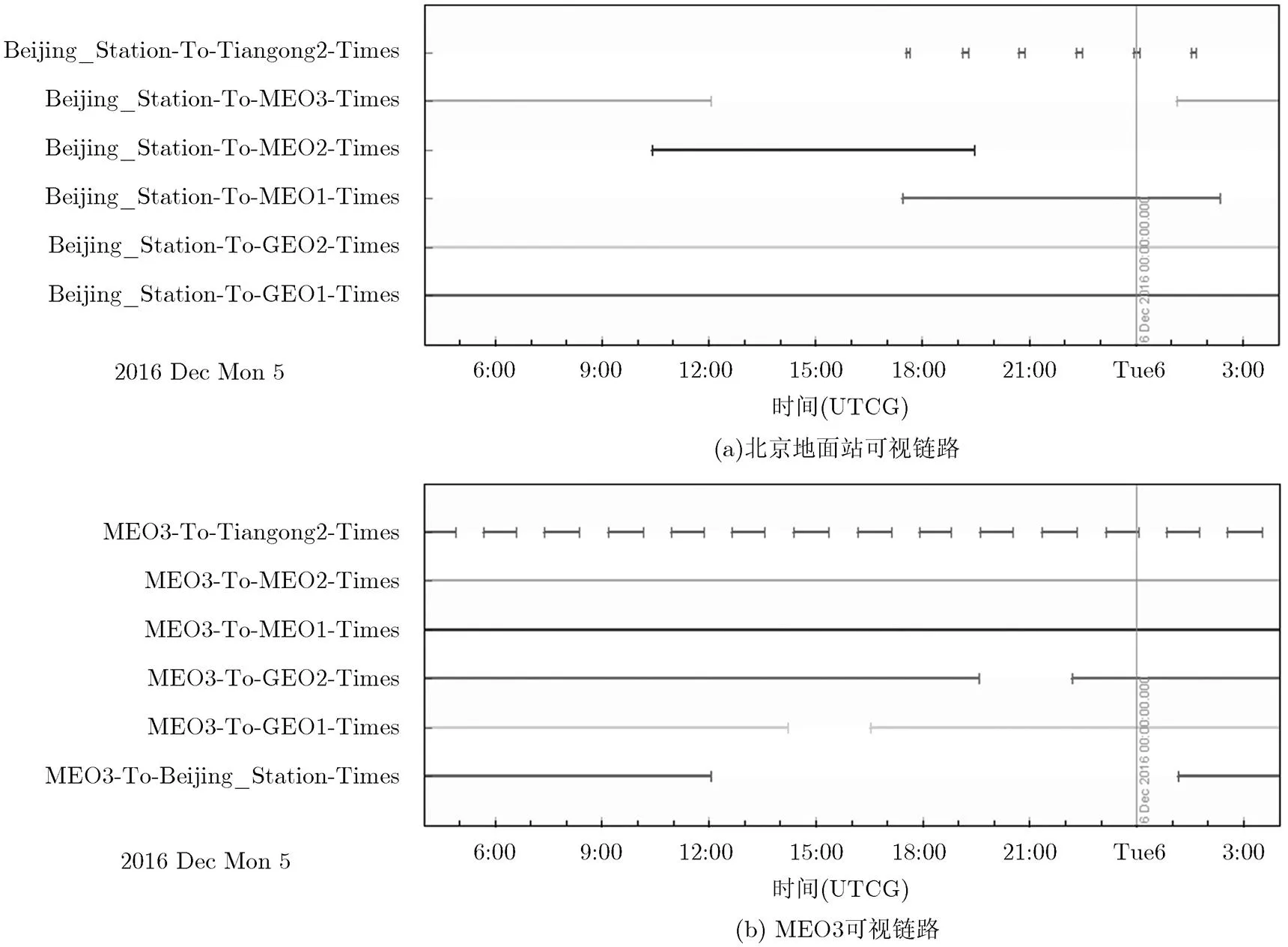
图5 时间同步可视链路变化

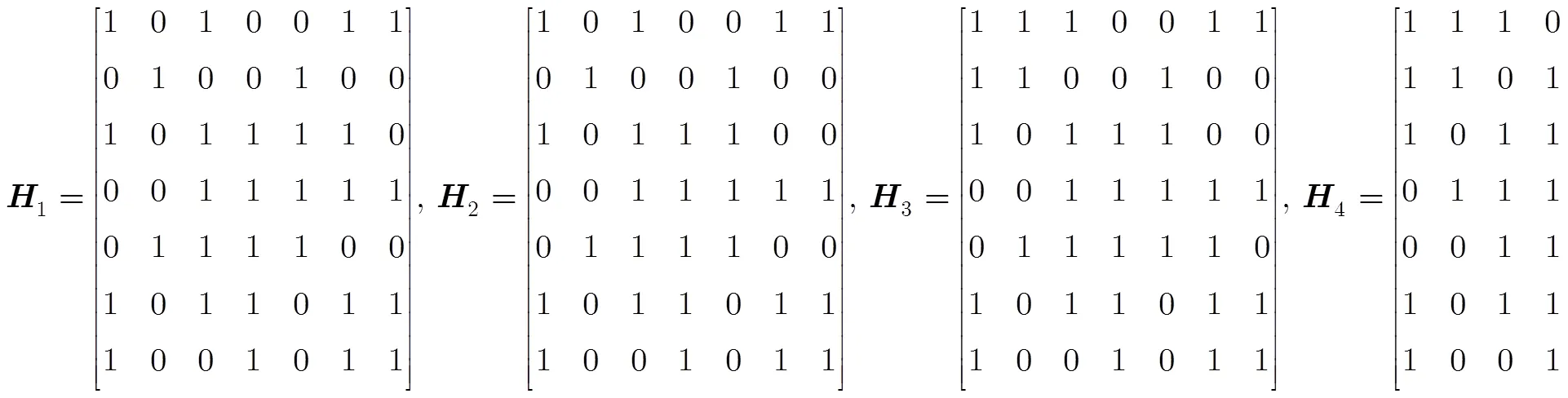
基于钟差不变时间的拓扑聚合图矩阵为

对各节点间链路时间同步精度进行统计分析，以时间同步精度作为链路代价得到时间比对代价矩阵，此处实验链路比对精度为随机定义。

表3不同时段的比对路径选择与观测误差

路径选择时间同步精度(ns) 时段1MEO3→GEO1→地面站0.98 时段2MEO3→GEO1→地面站0.98 时段3MEO3→天宫2→地面站0.50 时段4MEO3→GEO2→地面站0.92 均方值-0.87

对24小时内的时间同步精度变化进行实验，结果如图6所示。仿真分别基于固定可视链路、时变图模型以及拓扑聚合图模型进行实验，其中固定路由为MEO3与北京站不可见时依靠始终可见的另外两颗MEO星交替作为中继。可以看到，固定链路单纯依靠可视性进行路径选择，所实现的多跳时间同步精度较差；当比对节点直接可视或者网络拓扑长时间保持不变时，采用拓扑聚合图模型与时变图模型效果一致，当拓扑变化较快时，即该网络内的LEO星周期性与地面站间歇性可视情况下，基于时变图模型会进行频繁的路由切换，而拓扑聚合图模型可以始终最优路径进行时间同步。统计24小时数据，基于可视性固定链路的时间比对平均精度为0.9792 ns，采用时变图模型的时间比对平均精度为0.7768 ns，采用拓扑聚合图模型的时间同步精度提高为0.6359 ns。

改变时变图快照频度进行实验，对时变图模型以快照频度为间隔进行时间同步，统计24 h内时间同步误差均方根，实验结果如图7所示。对于基于时变图模型的时间同步，测量频度的提高并不能够使时间同步精度得到提高，主要原因就在于时变图割裂了节点在时间域上的连通关系，难以得到最优的时间同步路径。基于拓扑聚合图模型的时间同步，其测量精度与拓扑时变图的快照频度有关，更高频度的快照图聚合能够更逼真的反映节点在时间域上的连通关系，获得最优的路径选择。

对该构建的空间网络模型，统计24 h内所有空间节点与北京地面站节点进行时间比对精度的平均值。快照频度选取为15 min，采用时变图模型时，时间同步精度平均值为0.75 ns；采用基于拓扑聚合图模型时的时间同步精度为0.59 ns。

仿真实验验证了基于钟差不变性拓扑聚合图模型的有效性，基于该模型进行多跳中继时间同步，减少了时间比对路径选择次数，降低了时间比对次数，同时获得了更优的时间比对精度。

6 结论

本文以空间信息网络的时间同步业务为研究对象，针对误差模型和业务特点进行了分析，面向非实时高精度时间同步业务需求，提出了基于钟差相对不变性的空间信息网络拓扑聚合图模型。不同于面向通信业务的网络拓扑优化模型，该模型以时间同步业务为约束条件和优化对象，实现了从时间同步业务的角度对空间信息网络拓扑的刻画。基于该模型进行节点间多跳中继时间同步，以少量精度更高的测量代替多次精度相对较低的测量，在降低时间同步建链次数的同时，使时间同步精度得到提高，通过网络拓扑的优化建模实现了网络节点时间同步性能的提高，对于提高空间信息网络时间同步业务的链路资源利用效率和时间同步精度具有意义。

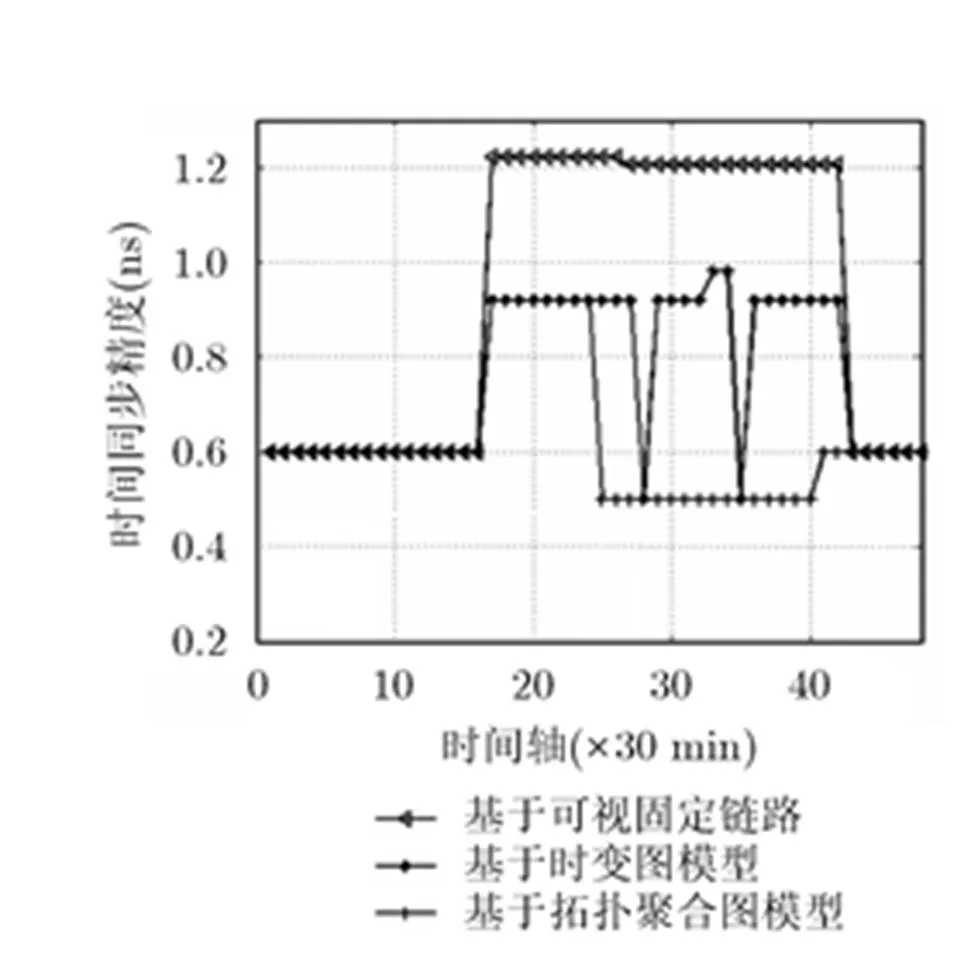
图6 24小时内北京站与MEO3的时间比对精度变化

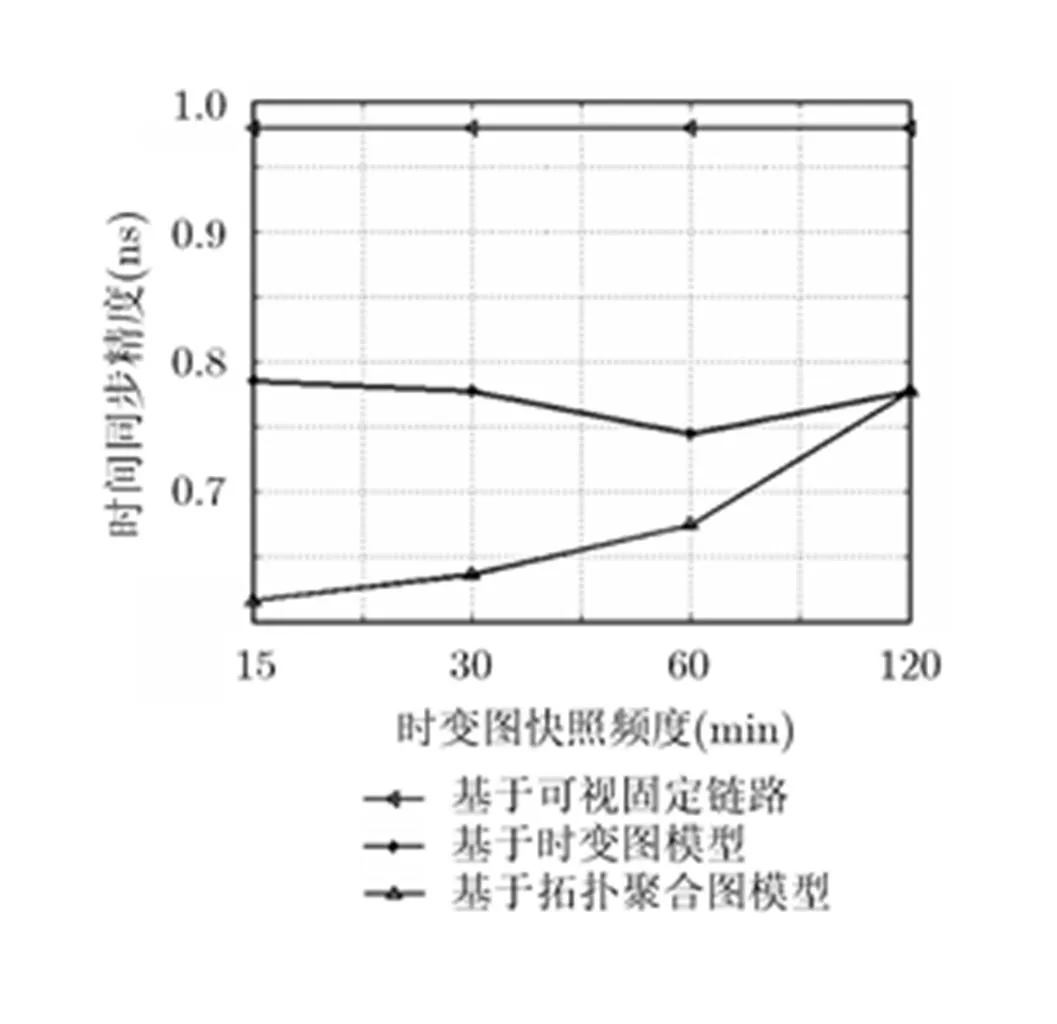
图7 不同时变图快照频度下的时间同步精度

[1] 李德仁, 沈欣, 龚健雅, 等. 论我国空间信息网络的构建[J].武汉大学学报(信息科学版)[J]. 2015, 40(6): 711-716. doi: 10.13203/j.whugis20150021.

LI Deren, SHEN Xin, GONG Jianya,. On construction of China’s space information network[J]., 2015, 40(6): 711-716. doi: 10.13203/j.whugis20150021.

[2] PULLIAM J, ZAMBRZ Y, ARMARKER A,. TSAT network architecture[C]. Military Communications Conference 2008 IEEE. San Diego, CA, 2008: 1-7. doi: 10.1109/MILCOM.2008.4753508.

[3] COOK K L B. Current wideband MILSATCOM infrastructure and the future of bandwidth availability[J]., 2010, 25(12): 23-28. doi: 10.1109/MAES.2010.5638785.

[4] The Integrated Space Infrastructure for global Communications [OL]. http: //www. isi-initiative.org/.2008.

[5] 张乃通, 赵康僆, 刘功亮. 对建设我国“天地一体化信息网络”的思考[J]. 中国电子科学研究院学报, 2015, 10(3): 223-230. doi: 10.3969/j.issn.1673-5692.2015.03.001.

ZHANG Naitong, ZHAO Kanglian, and LIU Gongliang. Thought on constructing the integrated space-terrestrial information network[J]., 2015, 10(3): 223-230. doi: 10.3969/j.issn.1673-5692.2015.03.001.

[6] 李贺武, 吴茜, 徐恪, 等. 天地一体化网络研究进展与趋势[J]. 科技导报, 2016, 34(14): 95-106.doi: 10.3981/j.issn.1000-7857. 2016.14.011.

LI Hewu, WU Qian, XU Ke,. Progress and tendency of space and earth integrated network[J].&, 2016, 34(14): 95-106. doi: 10.3981/j.issn.1000-7857. 2016.14.011

[7] LIU R, SHENG M, LUI K,. An analytical framework for resource-limited small satellite networks[J]., 2016, 20(2): 388-391. doi: 10.1109/ LCOMM.2015.2509993

[8] LI Yong, SONG Chaoming, JIN Depeng,. A dynamic graph optimization framework for multihop device-to-device communication underlaying cellular networks[J]., 2014, 21(5): 52-61. doi: 10.1109/ MWC.2014.6940433

[9] LIU R, SHENG M., LUI K,. Capacity analysis of two- layered LEO/MEO satellite networks[C]. 2015 IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, 2015: 1-5. doi: 10.1109/VTCSpring.2015.7145726.

[10] 燕洪成, 张庆君, 孙勇. 空间延迟/中断容忍网络拥塞控制策略研究[J]. 通信学报, 2016, 37(1): 142-150. doi: 10.11959/j.issn.1000-436x.2016016.

YAN Hongcheng, ZHANG Qingjun, and SUN Yong. On congestion control strategy for space delay/disruption tolerant networks[J]., 2016, 37(1): 142-150. doi: 10.11959/j.issn.1000-436x.2016016.

[11] 张威, 张更新, 边东明, 等. 基于分层自治域空间信息网络模型与拓扑控制算法[J]. 通信学报, 2016, 37(6): 94-105. doi: 10.11959/j.issn.1000-436x.2016120.

ZHANG Wei, ZHANG Gengxin, BIAN Dongming,. Network model and topology control algorithm based on hierarchical autonomous system in space information network[J]., 2016, 37(6): 94-105. doi: 10.11959/j.issn. 1000-436x.2016120.

[12] LI Hongyan and ZHANG Tao. A maximum flow algorithm based on storage time aggregated graph for delay-tolerant networks[OL]. Ad Hoc Networks(2017),http://dx.doi.org/ 10.1016/j.adhoc.2017.01.006.

[13] 杨文可, 孟文东, 韩文标, 等. 欧洲空间原子钟组ACES与超高精度时频传递技术新进展[J]. 天文学进展, 2016, 34(2): 221-237. doi: 10.3969/j.issn.1000-8349.2016.02.06.

YANG Wenke, MENG Wendong, HAN Wenbiao,. Advances in atomic clock ensemble in space of europe and ultraprecise time and frequency transfer[J]., 2016, 34(2): 221-237. doi: 10.3969/j.issn.1000- 8349.2016.02.06.

[14] 雷雨, 李变, 赵丹宁, 等. 一种高精度实时GPS卫星钟差预测算法[J]. 中国空间科学技术, 2014, 8(4): 39-45. doi: 10.3780/ j.issn.1000-758X.2014.04.006.

LEI Yu, LI Bian, ZHAO Danning,. Real-time prediction algorithm for high-accuracy GPS satellite clock offset[J]., 2014, 8(4): 39-45. doi: 10.3780/j.issn.1000-758X.2014.04.006.

[15] 杨富春, 李素英, 李斌, 等. 四种模型在卫星钟差短期预报中的应用研究[J]. 水利与建筑工程学报, 2014, 12(6): 199-204. doi: 10.3969/j.issn.1672-1144.2014.06.040.

YANG Fuchun, LI Suying, LI Bin,. Research on the application of four models used in the short-term prediction of satellite clock errors[J]., 2014, 12(6): 199-204. doi: 10.3969 /j.issn.1672-1144.2014.06.040.

蔚保国： 男，1966年生，研究员，研究方向为卫星导航系统总体设计.

鲍亚川： 男，1985年生，博士生，研究方向为卫星导航、高精度时间同步.

魏海涛： 男，1979年生，高级工程师，研究方向为卫星导航、高精度时间同步.

Time Synchronization Service Oriented Topology AggregationModel of Space Information Network

YU Baoguo BAO Yachuan WEI Haitao

(,050081,)(54,050081,)

The trend of heterogeneous node and functional diversification is presented in the development of space information network. The synchronization of network nodes is the technical foundation of task coordination of network nodes. The characteristic of time synchronization service of space information network is analyzed in this paper and the error model of multi-hop relay time synchronization is given. The concept of clock offset relative invariance is proposed based on the characteristic of non-real-time time synchronization, and a novel space information network topology aggregation model is given for time synchronization service. Differing from normal communication-service-oriented network models, the constraint condition of the model establishment is the performance of node clock and the time synchronization link, and the characteristic and requirement of time synchronization service is concerned. Simulation of space information network time synchronization is made according to the model. In the process of multi-hop relay time synchronization based on the model, less routing and linking number is needed. The link resource consumption is reduced, and the time synchronization precision is improved.

Space information network; Time synchronization; Relative invariance of clock offset; Topology aggregation

TN967.1

A

1009-5896(2017)12-2929-08

10.11999/JEIT170252

2017-03-29；

2017-08-31；

2017-10-27

通信作者：鲍亚川 baoyachuan@126.com

国家自然科学基金(91638203)，国家重点研发计划(2016YFB0502102)

: The National Natural Science Foundation of China (91638203), The National Key Research and Development Program (2016YFB0502102)