元线非直线型铧式犁几何与力学特性研究

徐锐良，刘美洲，郭志军，张 荣

(河南科技大学 车辆与交通工程学院，河南 洛阳 471003)



元线非直线型铧式犁几何与力学特性研究

徐锐良，刘美洲，郭志军，张 荣

(河南科技大学 车辆与交通工程学院，河南 洛阳 471003)

降低铧式犁耕作阻力，减少能源消耗，是国内外农业机械研究者一直非常关注的课题。铧式犁犁体曲面成型方法是元线沿着准线按照一定规律运动形成，元线与准线形式是影响铧式犁耕作阻力的两个重要因素。以BTU35犁体为基础，用三角函数曲线代替直线作为元线形成新犁体曲面，采用有限元分析方法，将两犁体曲面耕作阻力进行比较。研究发现：三角曲线作为元线形成的犁体曲面耕作阻力较小，在5、6、7km/h时耕作阻力分别比原犁体降低2.5%、4.1%、3.9%。结合直线与sin函数曲线曲率变化情况，可得出结论：变曲率犁体曲面更有利于降低耕作阻力。

犁体曲面；耕作阻力；三角函数；ANSYS

0 引言

我国是一个农业大国，每年约有1亿hm2的土地需要耕翻。铧式犁作为主要的耕作工具之一，每年要消耗大量的能源，犁体曲面形状直接影响着耕作质量的好坏与耕作阻力的大小[1]。如果能通过合理改善犁体曲面形状来降低耕作阻力，减少能源消耗，将会对我国农业经济的发展有着重要意义。针对如何优化犁体曲面，降低耕作阻力，国内外研究者曾做过很多努力。1968年，匈牙利研究者用滚子代替犁壁尾部，使土垡沿犁壁的运动由滑动摩擦变为滚动摩擦，从而减小犁壁与土壤之间的摩擦阻力，降低耕作阻力；但滚子犁翻土性能与覆盖性能都很差，又要增添滚子装置，导致成本提高[2]。1972年，苏联用聚四氟乙烯塑料覆盖犁体表面，生产出塑料犁，试图减小摩擦阻力。塑料犁在作业时有很好的减阻效果；但犁体磨损快，寿命短，成本也高[3]。20世纪70年代，上海市农科院农机所开始研究振动犁，发现犁体以恰当的振动频率、振幅、振动形式振动不仅可以使牵引阻力降低，且土壤破碎程度也很理想；但总能量减少并不显著，牵引力减少的动力不足弥补振动机构所消耗的动力，由于振动，又要增加很多附件，提高了造价，也减少了铧式犁的寿命[3]。吉林大学李建桥、任露泉教授从典型土壤动物蜣螂体表触土非光滑部位得到启发，在原来犁壁表面堆焊一系列凸点，设计了仿生非光滑犁壁，通过实验发现仿生非光滑犁壁具有很好的脱土性，耕作阻力较原来小，但却增加了表面堆焊这一工艺[4]。由于种种原因，上述方法并没有得到很好的推广。本研究从改变犁体曲面微观形状出发，采用正弦函数曲线代替原来的直线作为铧式犁成型中的元线，设计新犁体曲面，在ANSYS中进行动力学分析，将前后两犁体耕作阻力进行对比，旨在探索正弦函数作为元线形成的犁体是否具有降阻作用。

1 铧式犁犁体曲面建模方法

犁体曲面成型方法主要有水平直元线法、倾斜直元线法、曲元线法和翻土曲线法等几类[5]。本研究采用水平直元线法设计犁体曲面，所谓水平直元线法亦是一直元线沿着导曲线，并按照与沟壁间所夹元线角的变化规律，自下而上地移动所形成的连续曲面[5]。如图1所示，元线在移动过程中始终平行于水平面XOY，与沟墙面XOZ成一定角度，角度随高度的增加按一定公式计算，且在移动过程中元线始终与导曲线接触。本研究原犁体曲面采用BTU35，参数如表1所示，新犁体采用正弦函数曲线代替BTU35犁体中的直元线。正弦函数曲线振幅A取5mm[6]，铧刃线长度作为一个函数周期，ω按如下公式计算，有

Lcos(θ)=0

L=T=2π/ω

式中L—铧刃线长度；

θ—BTU35犁体铧刃线起始角，θ=42°；

D—BTU35犁体耕宽，D=375mm。

可得：A=5，ω=0.0124 5。

正弦函数曲线为y=5sin(0.012 45x)。

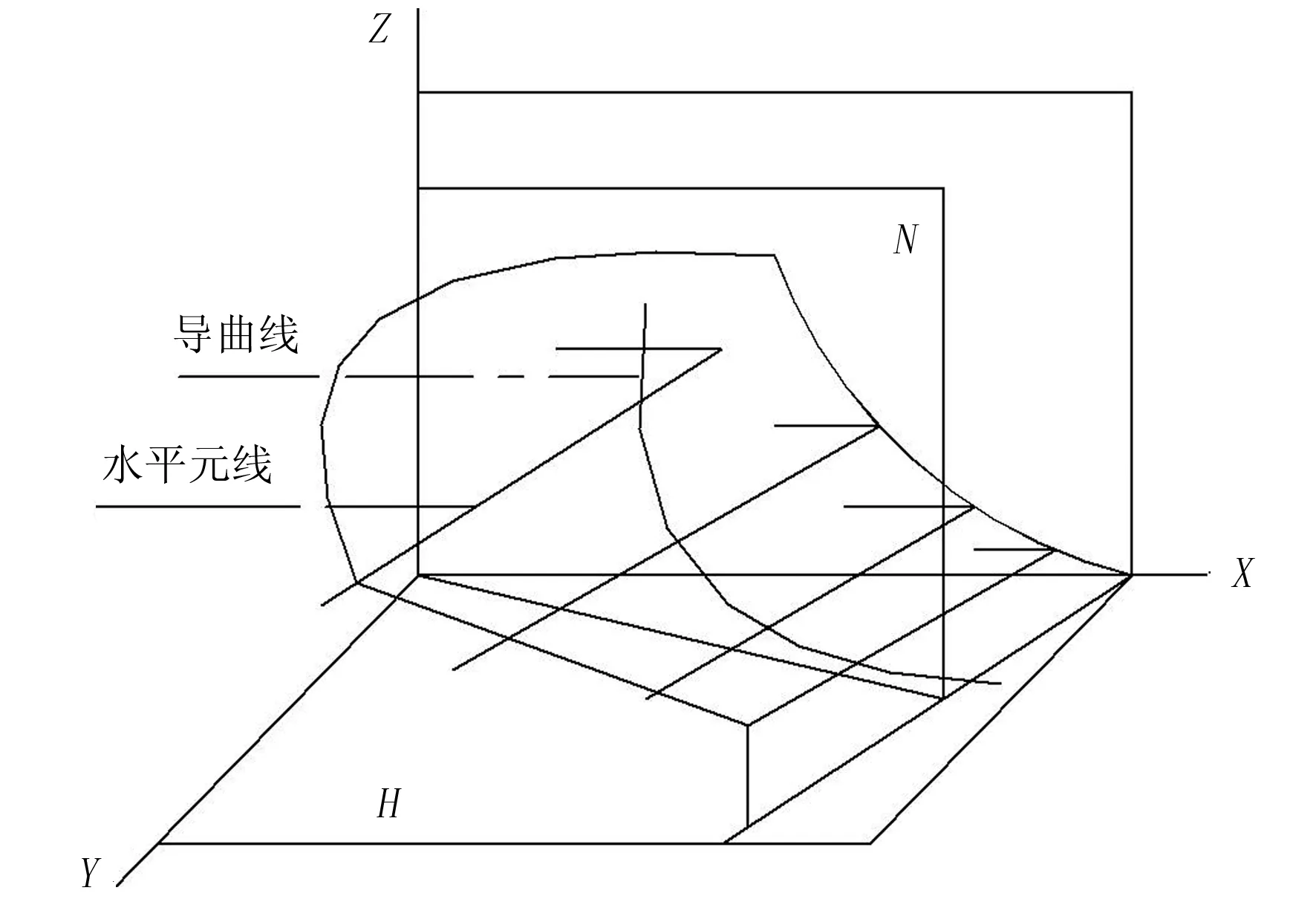
图1 犁体曲面形成示意图Fig.1 Schematic diagram of forming plow surface表1 BTU35犁体参数Table 1 The parameters of BTU35 plow

项目单位数值耕深mm270耕宽mm375胫刃线高mm344顶边线最大高度mm430翼边线夹角(°)35导曲线距铧尖距离mm323导曲线段中直线长mm60安装角(°)30切线夹角(°)115起始元线角(°)42中间最小元线角(°)40顶部最大元线角(°)115

2 元线曲率

元线曲率变化趋势在微观上表现为土壤应力波动程度，在宏观上表现为犁体耕作阻力变化情况。以下分析直线与正弦函数曲线曲率变化趋势及元线曲率几何特征与土壤应力波动之间的关系。

2.1 元线曲率分析

直线曲率半径为无穷大，曲率恒为零。正弦函数曲率变化如图2所示，随着x的增大，正弦函数曲线曲率呈现波动趋势，总体变化表现为先增大后减小至零，之后反向增大再减小接近于零；沿x轴正向，正弦函数函数曲线曲率出现3次极值，极大值、极小值交替出现。

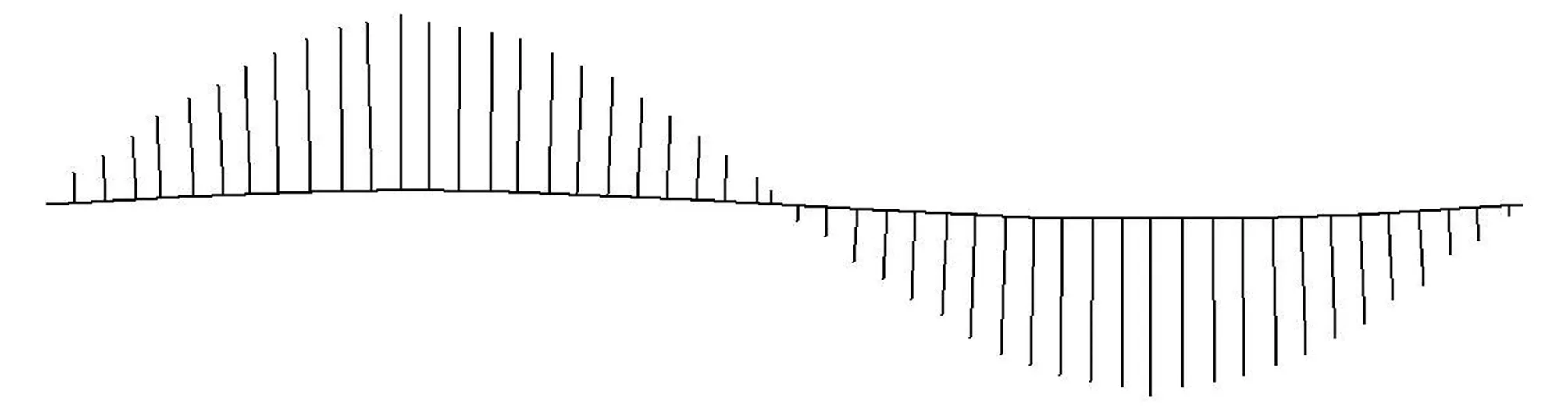
图2 正弦函数曲率变化图Fig.2 Curvation variation of sine function

2.2 元线曲率几何特征与土壤应力波动间的关系

1)直线型元线：具有平行于曲线本身的曲率半径中心轨迹以及自平行的曲率半径。自平行的曲率半径，表现为土壤沿该直线型元线犁体曲面侧向移动时，法向应力不会发生变化。位于元线同一侧的曲率半径反映了犁体曲面对土壤的法向作用力方向未发生变化。

2)正弦函数型元线：曲率趋势总体呈波动状态，曲率半径大小不断变化，且位于曲线的两侧。分布于元线两侧不同的曲率半径，微观表现为土壤沿该犁体曲面侧向运动时，土壤所受法向应力不断发生变化，且应力方向发生一次改变，宏观表现为曲面对作用其上的土壤具有破碎作用，这将减小犁体曲面前方土壤因挤压形成的高压应力，从而在宏观上减小犁体工作阻力。

3 仿真分析

3.1 有限元模型的建立

ANSYS分析功能强大，建模能力欠佳，对于曲面较为复杂犁体曲面可在SolidWorks中建模。模型建完后保存为.XT格式，然后导入ANSYS进行显式动力学分析。为了简化计算，结合实际情况，将土壤模型定为一个长宽高为1.5m×0.4m×0.32m的长方体。土壤模型简单，可直接在ANSYS中建模。土壤-犁体曲面模型建完后开始生成有限元模型，有限元模型是有限元分析的基础，研究采用网格划分间接生成有限元模型。按照有限元原理，网格划分越多，计算值越接近于实际值，但同时计算量将大大增加。犁体曲面形状较为复杂，微观是一个三面锲形状，对其只能采用自由网格划分(free)，划分为4面体4节点的网格，智能尺寸采用9级精度。对于形状比较规则的土垡，可采用扫略(sweep)方式进行网格划分，划分为6面体8节点网格，网格数量采用控制边长法。

3.2 ANSYS/LS-DYNA中土壤切削模型参数设置

1)单元类型。根据土壤切削模型现有研究成果，犁体和土垡单元类型均设置为3维8节点solid164实体单元。积分模式采用Lagrange全积分模式，不仅能提高计算精度，而且可以控制沙漏模式出现。单点积分虽可减少节点计算个数，提高运算效率，却会降低计算精度。

2)材料模型。材料模型的定义是数值模拟中一个非常重要的环节，直接影响着数值模拟的精度与可靠性。犁体材料模型选用16Mn，参数如表2所示[7]。用刚性体模型定义有限元模型中刚硬部分可以大大缩减显式分析计算时间，结合犁体材料模型，将犁体材料定义为刚体。根据土壤物理及力学特性分析，对其采用LS-DYNA中的塑性随动材料模型，土壤模型材料特性参数值如表3所示[7]。

表2 犁体材料特性参数Table 2 Material properties of plow

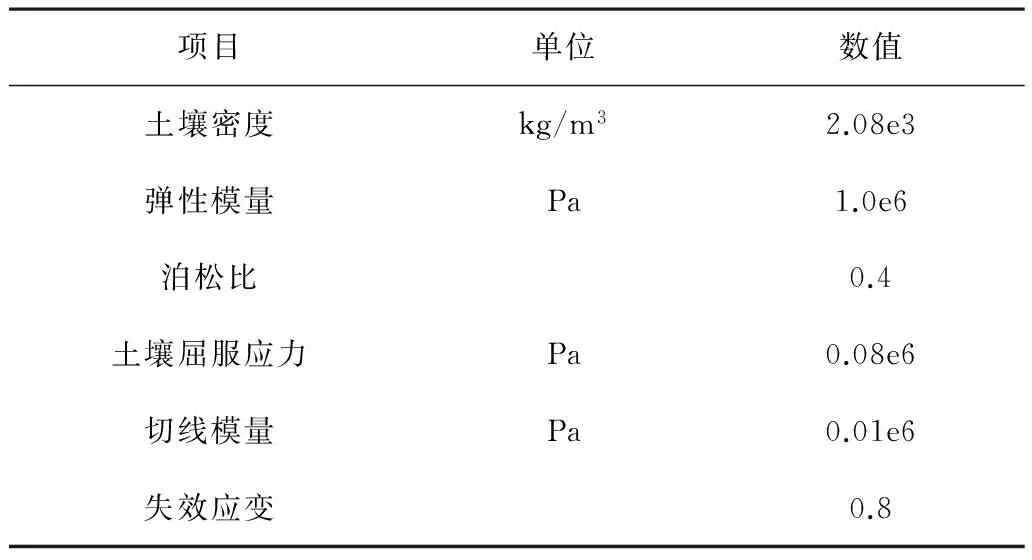
表3 土壤材料特性参数Table 3 Material properties of soil

3)接触模式。接触算法是程序用来处理接触面的方法，在LS-DYNA接触面处理算法中，当一个物体穿透另一个物体的面时，使用面面接触算法，当单元失效发生时，使用侵蚀接触算法[8]。铧式犁耕作过程中，土壤作为受体被切削破坏侵，因此犁体与土壤接触类型采用面面侵蚀接触(Surface to Surface-Eroding)，接触因子设置为0.2。

4)约束、载荷设置。正常作业情况下，犁体一般沿直线切削土壤，因此约束犁体除沿z轴平行移动外的所有自由度。从z轴负正方向看，约束土垡底面、左侧面、后视面所有自由度。实际中，待切土壤应为半无界区域，为了真实反映土壤之间作用力，对上述3个面施加非反射边界条件。载荷设置为犁体以5、6、7km/h沿z轴方向切割土壤。

5)输出设置。输出文件选择可用LS-Prepost读入的LS-DYNA类型，并在ASCII输出文件控制中添加RCFORC，用于输出接触面接触反力。

全部参数设置完后，开始求解，直到界面出现“Solution is done!”，说明计算完成。

4 结果分析

LS-Prepost是LSTC公司专门为LS-DYNA求解器开发的高级有限元前后处理软件，打开LS-Prepost软件后，首先读取结果文件d3plot，可显示犁体切割土壤全过程，如图3所示。

图3 土壤等效应力云图Fig.3 Equivalent stress nephogram for soils

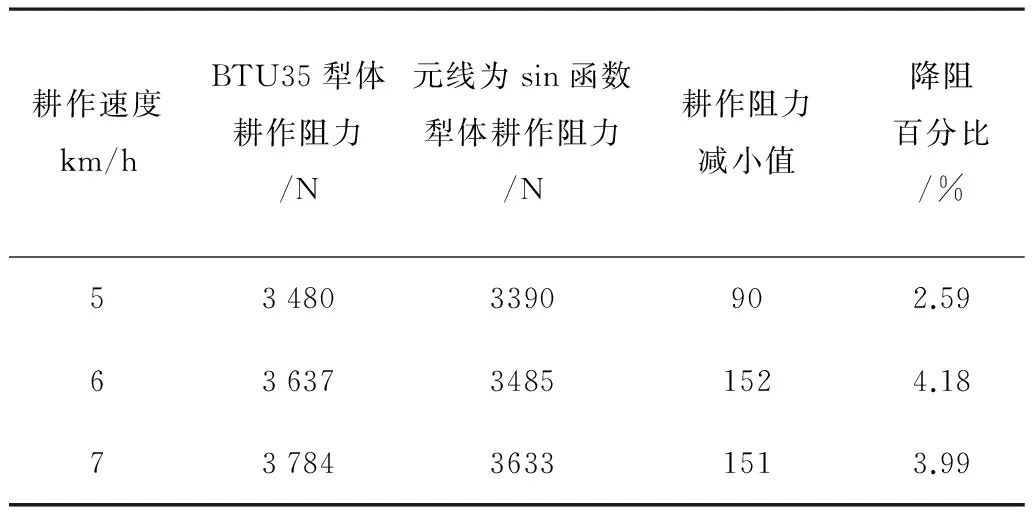
打开ASCII中的rcforce文件，可显示犁体总耕作阻力随时间变化曲线图，如图4所示。用记事本打开rcforce文件，可得犁体在各个时刻所对应的耕作阻力数据，如图5所示。把数据导入Excel中进行处理，可求出犁体作业过程中所受的平均耕作阻力，如表4所示。

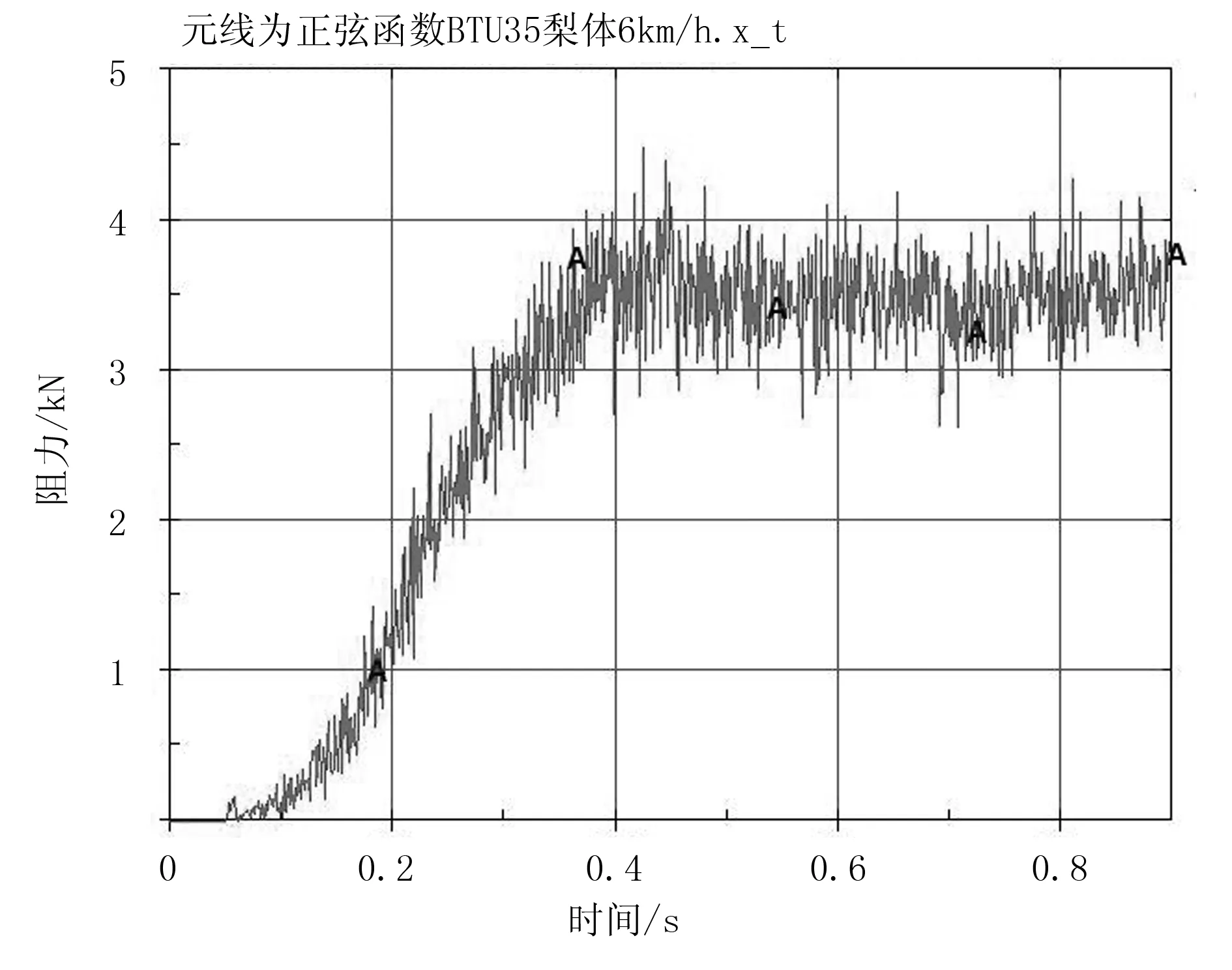
图4 铧式犁总耕作阻力-时间曲线Fig.4 Curve of operating resistance-time of plow

图5 铧式犁耕作阻力部分数据Fig.5 Partly data of plow’s operating resistance表4 犁体平均耕作阻力Table 4 The average resistances of plow

耕作速度km/hBTU35犁体耕作阻力/N元线为sin函数犁体耕作阻力/N耕作阻力减小值降阻百分比/%534803390902.596363734851524.187378436331513.99

4.1 切削过程中土壤应力变化

从图3中可看出：元线为正弦函数BTU35犁体以6km/h速度切削过程中土壤应力变化情况。在0.135s，铧式犁犁铧铧尖首先进入土壤，土壤开始变形，应力发生变化，此时最大应力为71 088Pa，发生在单元6 343上；在0.378s，铧式犁已部分进入土壤，犁体的铧刃和胫刃分别沿水平方向和铅垂方向将土壤切开，形成一个具有一定宽度和深度的土垡，此时最大应力为80 132.7Pa，发生在单元8254上;在0.684s与0.828s，土垡已全部进入土壤，切削过程趋于稳定阶段，此时最大应力分别为81 962、81 715.3Pa，发生在单元34 415与33 017上。从整个动态画面及稳定时刻后土壤应力变化情况可知整个切削过程比较稳定。

4.2 铧式犁阻力分析

由图4可知：随着时间变化，切削深度不断增加，耕作阻力逐渐增大，直到切削过程进入稳定阶段，耕作阻力在一个值附近上下波动。

由图5可知：在相同时刻，犁体与土壤所受界面反力大小相等，方向相反。0.4～0.9s为稳定时刻，把此时间段耕作阻力数据导入Excel进行处理，可得到此犁体以6km/h速度切削土壤时平均耕作阻力。

由表4中可知：随着作业速度增加，耕作阻力也在增大。元线为三角函数曲线BTU35犁体比原BTU35犁体耕作阻力小，这与三角函数曲线和直线曲率变化不同有着密切关系。元线为正弦函数犁体耕作阻力较小与其曲线曲率出现3次极值点有关，因为此元线犁体可使土壤应力场出现波动现象。一方面，土壤沿着此变曲率元线犁体曲面侧面滑动时，所受应力大小会出现波动现象，应力方向也会发生改变，这将提高碎土率，有利于降低阻力；另一方面，犁体曲面垂直方向土壤单元应力波动可使犁体前方被压实的土壤松碎，最终获得较小阻力。

5 结论

1) 应用ANSYS/LS-DYNA软件可以对犁体土壤切削模型进行较好的数值模拟仿真实验。

2) 用三角函数曲线作为元线形成的犁体比用直线作为元线形成的犁体耕作阻力小。

[1] 北京农业机械化学院.农业机械学(上册)[M].北京：中国农业出版社，1992：27-33.

[2] 高尔光.滚子犁的工作阻力[J].粮油加工与食品机械，1974,5(2)：11-14.[3] 高尔光.减少耕作部件牵引阻力的途径[J].粮油加工与食品机械，1980,11(3)：33-35.

[4] 李建桥，任露泉.减粘降阻仿生犁壁的研究[J].农业机械学报，1996,27(2)：3-4.

[5] 中国农业机械化科学研究院.农业机械设计手册(第1版)[K].北京：中国农业科学技术出版社，2007：188-192.

[6] 张毅，周志立.仿生圆盘犁犁体设计与制作[J].洛阳工学院学报，2002,23(3)：2-3.

[7] 庞承妮.1LD-440型深耕犁的仿真研究[D].南宁:广西大学，2005.

[8] 张红松.ANSYS14.5/LS-DYNA非线性有限元分析实例指导教程[M].北京：机械工业出版社，2013：114-115.

Abstract： Reducing the working resistance and cutting down the energy consumption has been an important subject for domestic and foreign agricultural machinery researchers.Plow-surface is formed when the basic line move along the directrix according to certain rules.The basic line and directrix are two important factors to affect the plow’s working resistance.Research on the base of BTU35, the new plow is designed by using trigonometric function curve instead of straight line as the baisc line.The working resistances are analyzed and compared with finite element method.It was discovered that the new plow reduced working resistance by 2.5 percents in 5km/h,4.1 percents in 6km/h, 3.9percents in 7km/h.Taking the condition of straight line and sine function currature changes into consideration,we can draw a conclusion that the variable curvature plow has better drag reduction effect.

ID:1003-188X(2017)03-0022-EA

Study on Geometrical Properties and Working Resistance Characteristics of Non-linear Basic Line Plow

Xu Ruiliang, Liu Meizhou, Guo Zhijun， Zhang Rong

(College of Vehicles and Traffic Engineering,Henan University of Science and Technology, Luoyang 471003,China)

plow surface；working resistance；sine function；ANSYS

2016-02-15

国家自然科学基金项目(51175150)

徐锐良(1966-),男，河南洛阳人，副教授，硕士生导师，(E-mail) lyxrl@163.com。

刘美洲(1988-)，男，河南周口人，硕士研究生，(E-mail)472050529@qq.com。

S222.12+1

A

1003-188X(2017)03-0022-04