“Y”型果树动力学模型仿真及试验的研究
2017-12-16刘子龙王春耀罗建清魏庭鹏吕梦璐
刘子龙,王春耀,罗建清,魏庭鹏,吕梦璐
(新疆大学 机械工程学院,乌鲁木齐 830047)
“Y”型果树动力学模型仿真及试验的研究
刘子龙,王春耀,罗建清,魏庭鹏,吕梦璐
(新疆大学 机械工程学院,乌鲁木齐 830047)
为了在研究分析果树振动特性时使问题简化,提出了用质量—弹性元件系统来建立果树力学模型的方法。为验证该方法的有效性,选择将“Y”型果树主干L0、主枝L1、侧枝L2视为3个质量块,建立三自由度果树振动模型,并运用MatLab中Simulink子系统封装技术对所建立的振动模型进行仿真运算,将得到的仿真结果与试验结果进行比较,得出主干L0、主枝L1、侧枝L2的加速度时域变化曲线。结果表明:仿真与试验结果吻合程度较好,建立的果树三自由度模型能够比较好地反映果树振动情况,用质量—弹性元件系统来建立果树力学模型的方法是切实可行的。同时,通过对果树共振频率的研究,确定25Hz左右为较合适的采摘激振频率,可为林果振动采摘收获机的参数优化提供必要的理论基础。
“Y”型果树;动力学模型;Simulink;共振频率
0 引言
新疆是著名的瓜果之乡,林果业已成为新疆发展的产业支柱。随着种植规模的扩大,每到收获季节需要投入大量的劳动力,人工收获水果的速度缓慢且成本较高,若要大面积发展水果种植,必须要依靠机械化来提高采摘效率[1]。目前,比较常用的机械化振动采收器械是通过振动式或冲击式激振果树,使果实脱落,能够快速、有效地分离成熟果实,适合大面积、规模化果品生产[2]。国内外有不少学者对机械振动式果实采收机理进行了相关研究: 1980年,Pacheco和Rehkugler采用撞击采摘原理,设计了一种用弹簧力撞击果树的收获机,其弹簧力的撞击速度最高可达5.16m/s,适合对中型大小的苹果树进行收获[3]。Kececioglu等人在利用惯性振摇器对橄榄进行收获时发现:当频率为20~28Hz、振幅为20~30mm时,收获效果最好,且果实脱落效率与激振频率和振幅有关[4]。Yung和Fridley为了分析整棵树的动态特性与振动激励参数关系,将果树简化为由树干—枝条、树叶—嫩枝、果实—果柄3种不同力学特性单元组成的集合体进行研究[5]。Castro-Garcia等人运用模态分析研究了果树的振动参数、固有频率和阻尼比[6]。郑甲红等人对树体枝干进行三维实体建模,并进行模态分析和频率谐响应分析,得出激振频率为24Hz时振幅较好[7]。张敏敏等人通过试验的方法将海棠果树的密度、阻尼系数、等效质量、等效刚度等果树谐振系统物理参数进行了测定[8]。
针对果树力学模型的建立,Zoltán Láng[9-12]做了一系列的研究,并指出:首先,果树在振动时树干的运动与各分枝的运动是相互独立的,即树干在分叉处的上下部分具有良好的线性关系;其次,在只考虑果树的结构阻尼、忽略粘性阻尼的前提下,将树干—树枝力学模型简化为双自由度的质量—刚度—阻尼力学模型时,较为准确。本文在Zoltán Láng提出的双自由度模型基础上,将“Y”型果树等效为三自由度模型,并进行了相关仿真与试验对比,从而验证了模型的有效性。
1 果树模型建立与仿真
1.1 果树振动系统动力学模型的建立
本次试验研究对象为“Y”型海棠果树,各测点安装实物图与简化图分别如图1、如图2所示。
由于生物系统的复杂性及多样性,在研究分析果树振动特性时,为了使问题简化,可以用几个质量—弹性元件系统来建立果树力学模型。因此,将“Y”型果树建为如图3所示的三自由度振动模型。根据张敏敏等人对海棠果树谐振系统物理参数的测定,本次研究“Y”型海棠果树的谐振系统物理参数如表1所示。
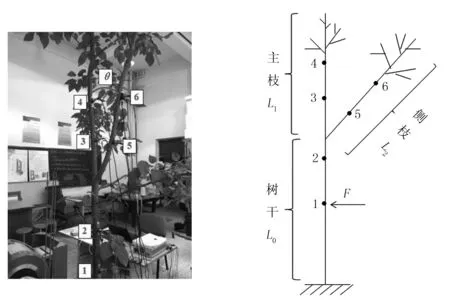
图1 试验现场 图2 果树简化图
Fig.1 Testing site Fig.2 The fruit trees simplified diagram

图3 果树三自由度力学模型

平均密度ρ/kg·m-3平均直径D/mm长度L/mm等效质量M/kg等效刚度K/N·mm-1等效阻尼C/N·S·mm-1树干L035.0414280.84780.62.335主枝L180923.5216360.73473.041.003侧枝L220.2615740.63440.070.559
1.2 果树振动微分方程的建立
根据上述力学模型,建立果树振动微分方程为[12-13]
将上述微分方程组表示成矩阵形式,则
方程可写为更为一般的形式,则
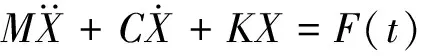
1.3 MatLab/Simulink模型的建立
采用MatLab中Simulink子系统封装技术[14],对上述所建立的振动微分方程进行仿真运算并输出,最后得出系统分别在5、7、9g激振载荷作用下的树干、树枝的加速度在时域内的变化曲线,如图4~图7所示。

图4 系统封装图
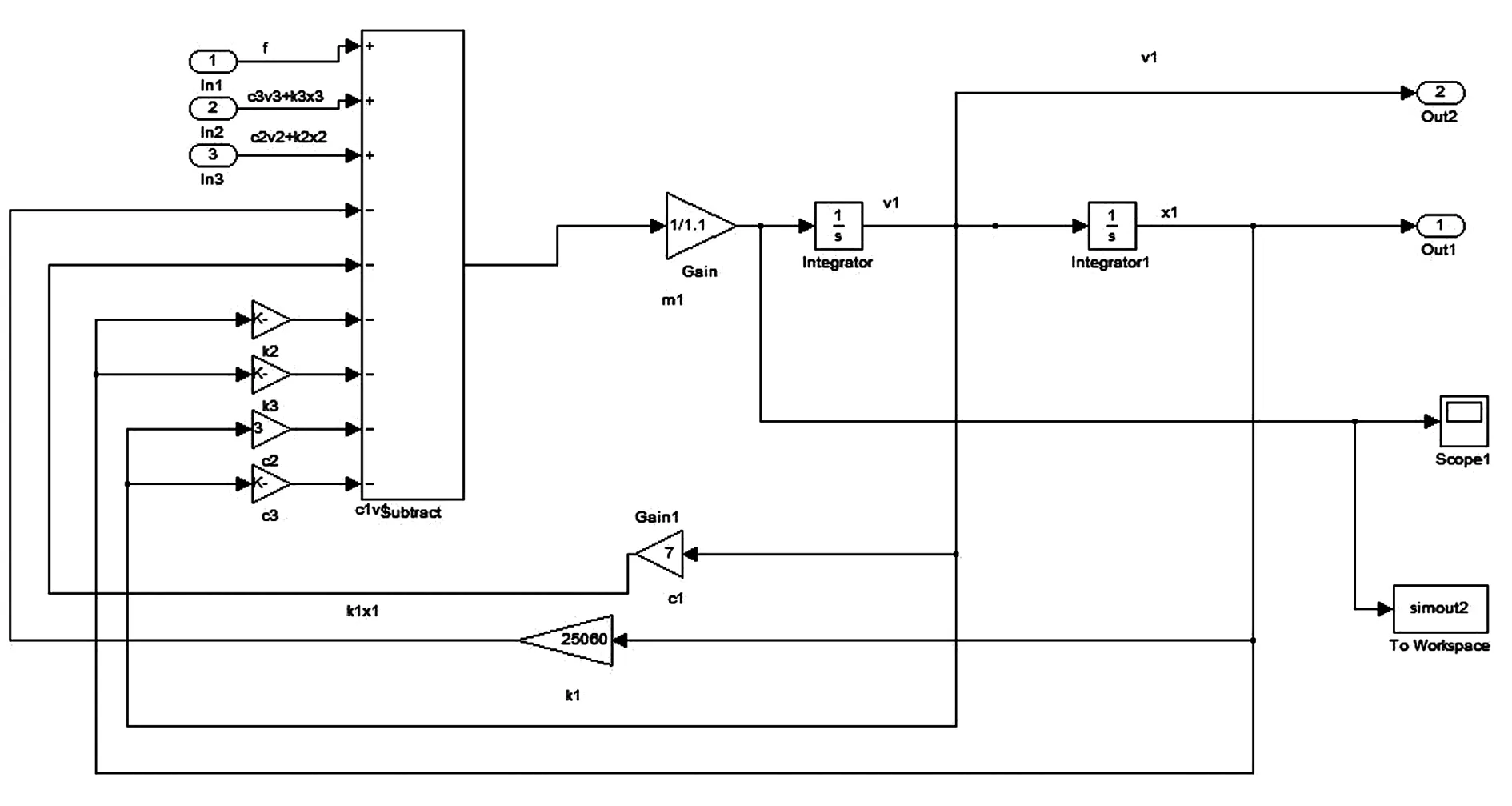
图5 子系统Subsystem1内部图
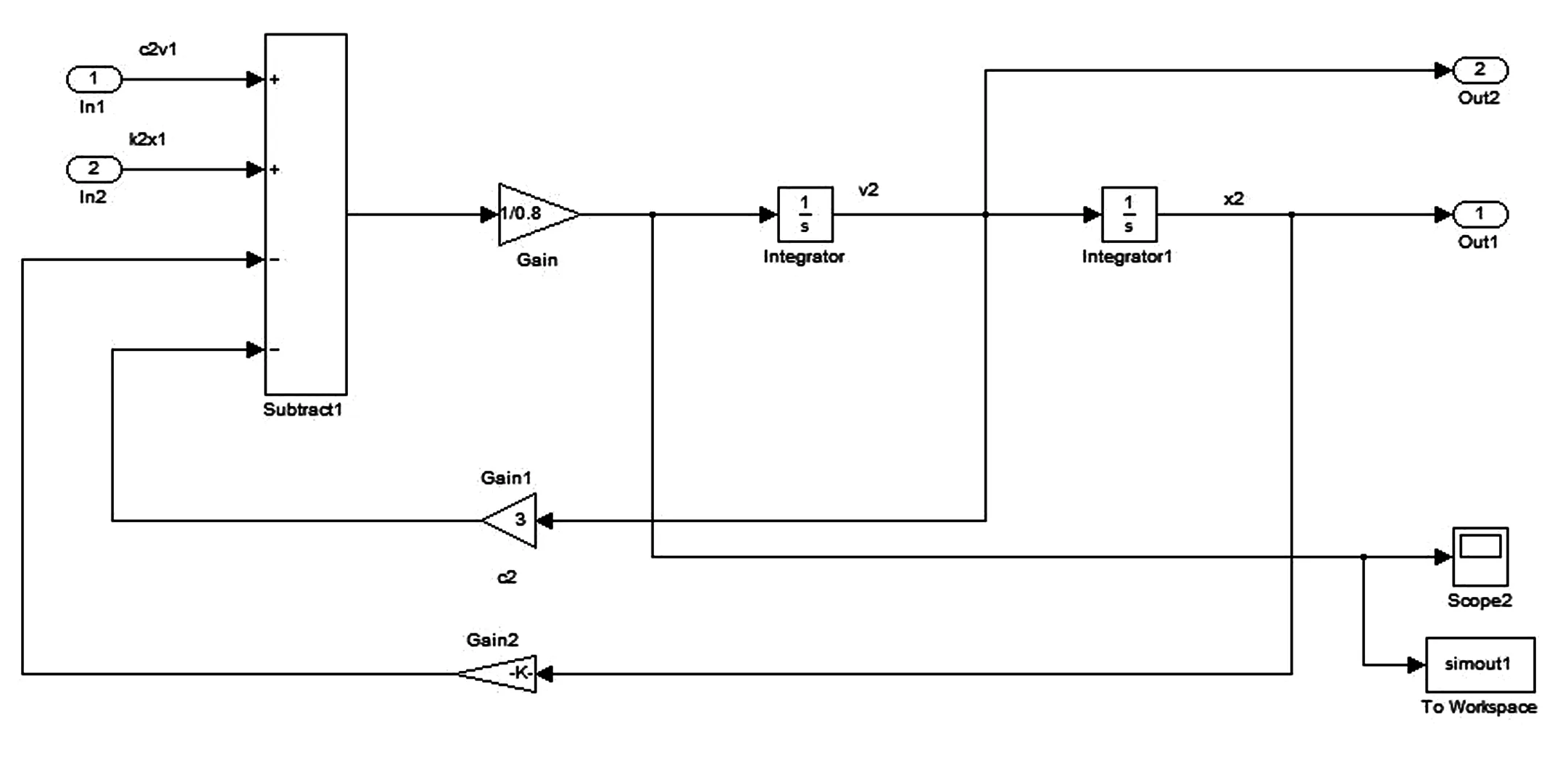
图6 子系统Subsystem2内部图
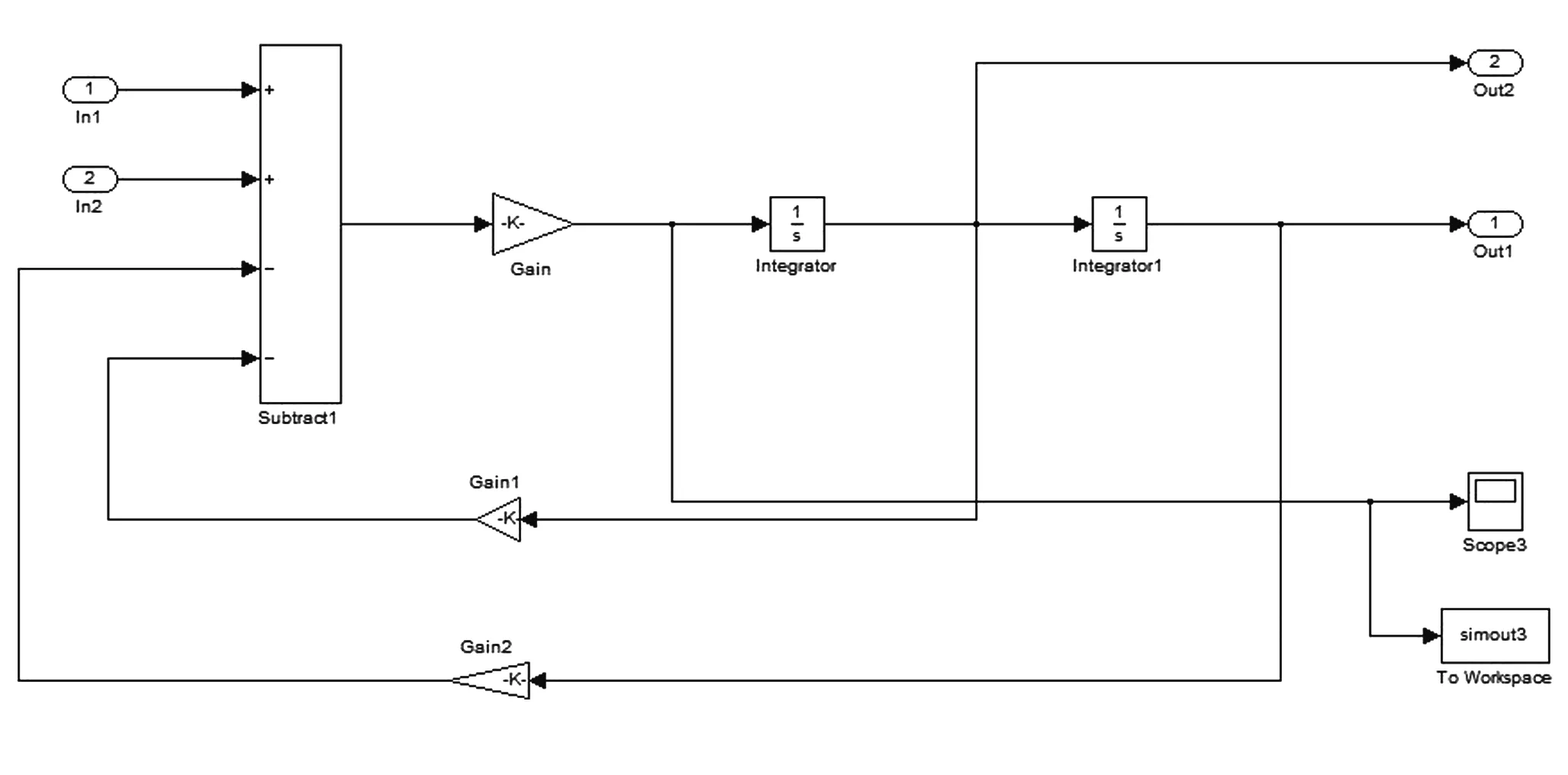
图7 子系统Subsystem3内部图
2 材料与方法
2.1 试验设备
试验设备为振动试验台DC-600-6、SV-0505水平滑台、功率放大器SA-5、RC-300-2振动控制仪、DH5922N动态信号测试分析系统、压电式加速度传感器DH311E及GHDAS软件等。
2.2 试验材料
试验样本为新疆地区有着5年树龄的海棠果树。
2.3 试验过程
树干底部用固定加持装置固定,在距离树干底部70cm处安装1号加速度传感器,距离树干底部120cm处安装2号加速度传感器,主枝上距离分叉点20cm处安装3号加速度传感器,主枝上距离分叉点40cm处安装4号加速度传感器,侧枝上距离分叉点20cm处安装5号加速度,主枝上距离分叉点40cm处安装6号加速度传感器,简化模型如图2所示。在测点1处分别施加加速度为5、7、9g的瞬时冲击载荷。设置采样频率为500Hz,利用DH5922N动态信号测试分析系统采集信号。将2号加速度传感器所测得的数据作为树干L0的试验数据,将3、4号加速度传感器测得的数据作为主枝L1的试验数据,将5、6号加速度传感器测得的数据作为侧枝L2试验数据。
2.4 试验结果与仿真结果比较
试验与仿真曲线如图8~图10所示。
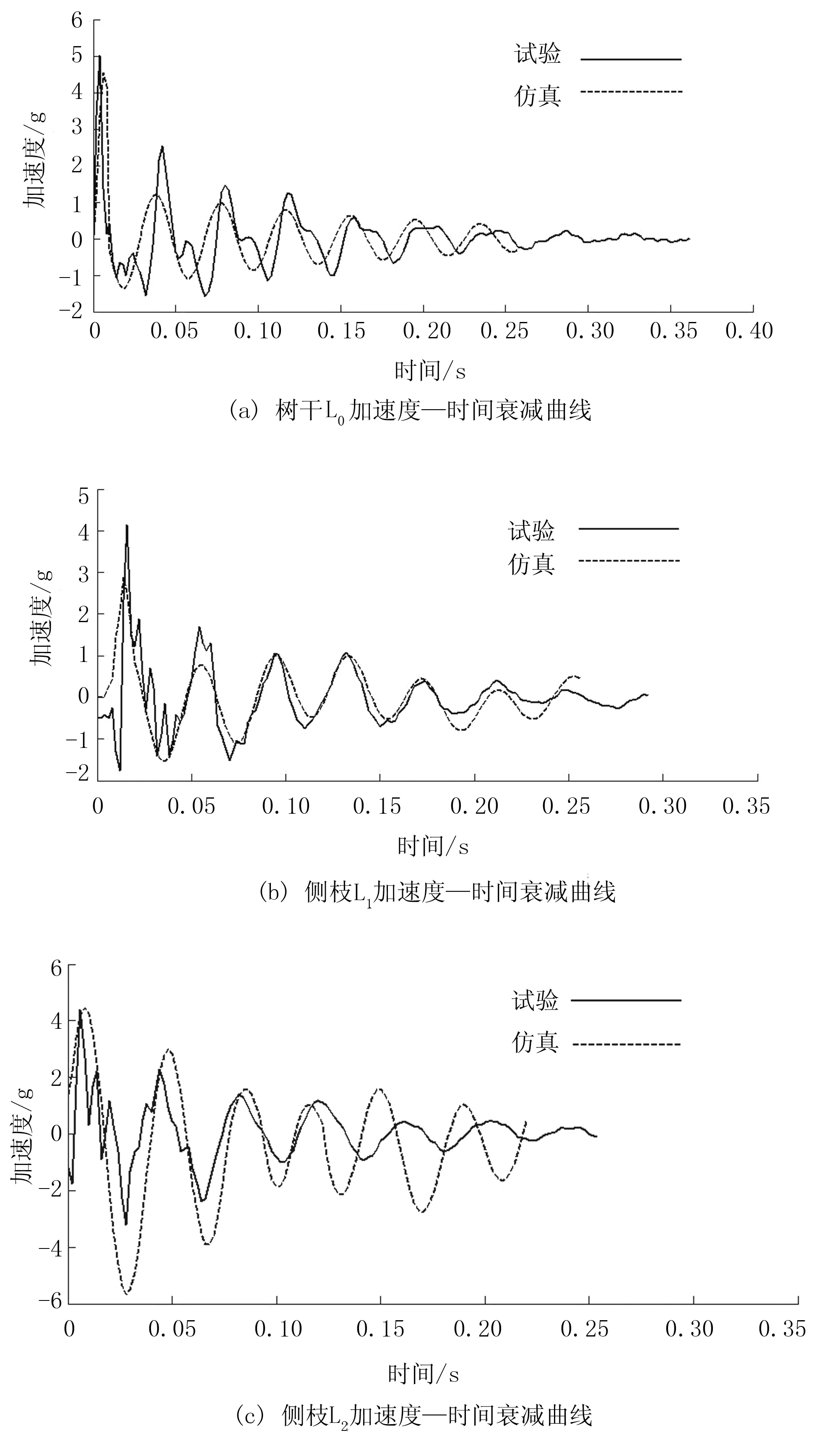
图8 5g载荷作用下试验与仿真曲线
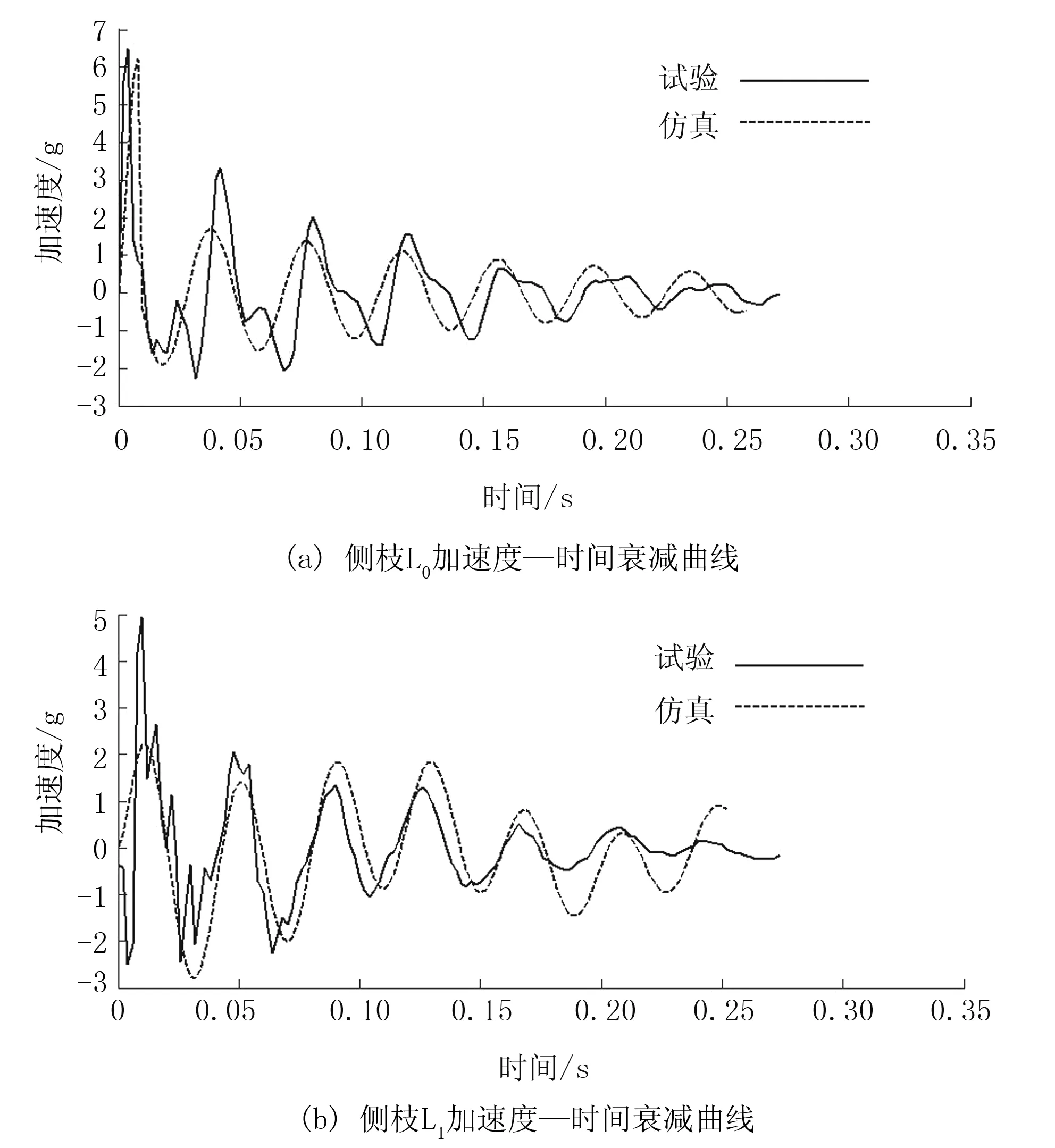
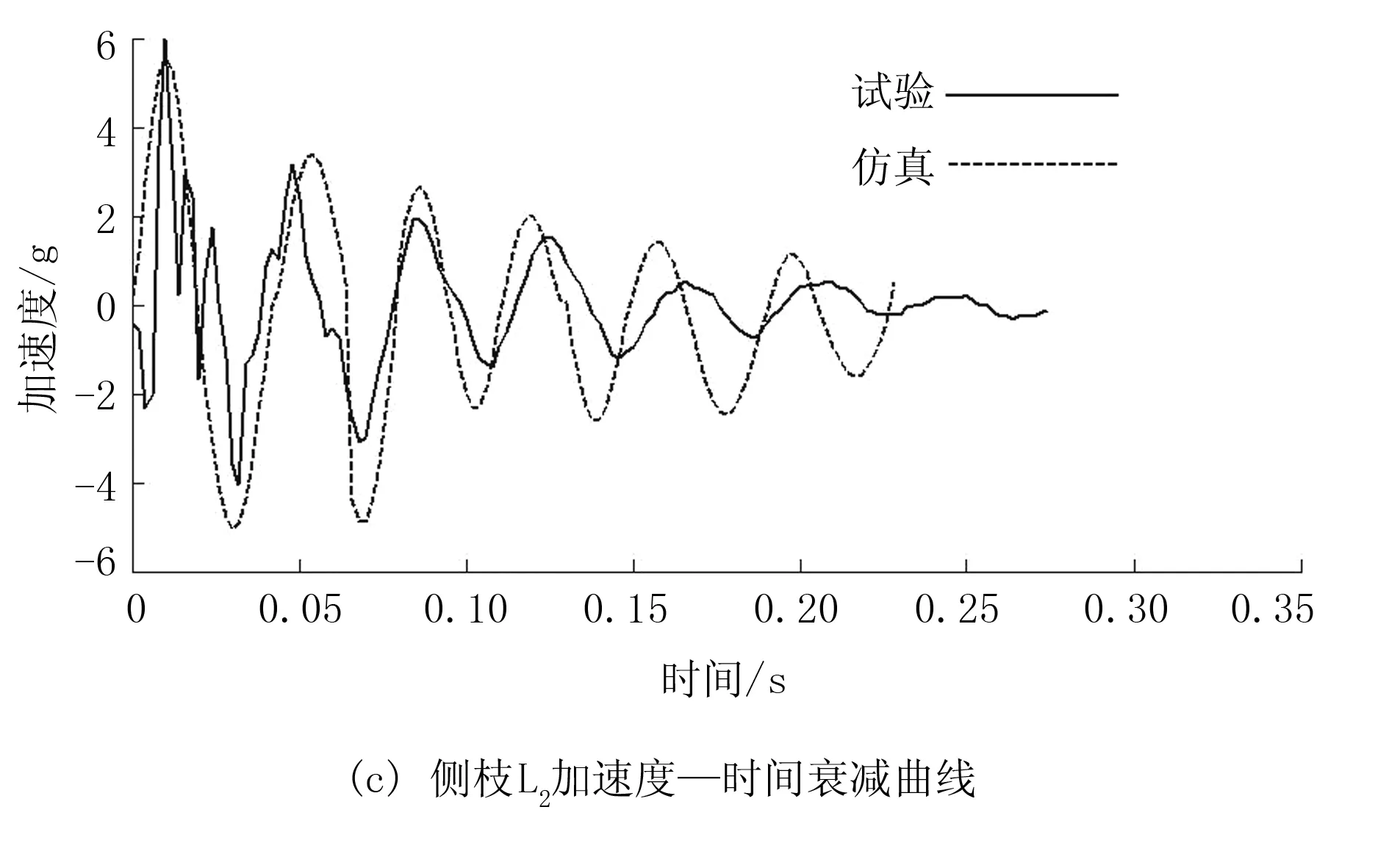
图9 7g载荷作用下试验与仿真曲线
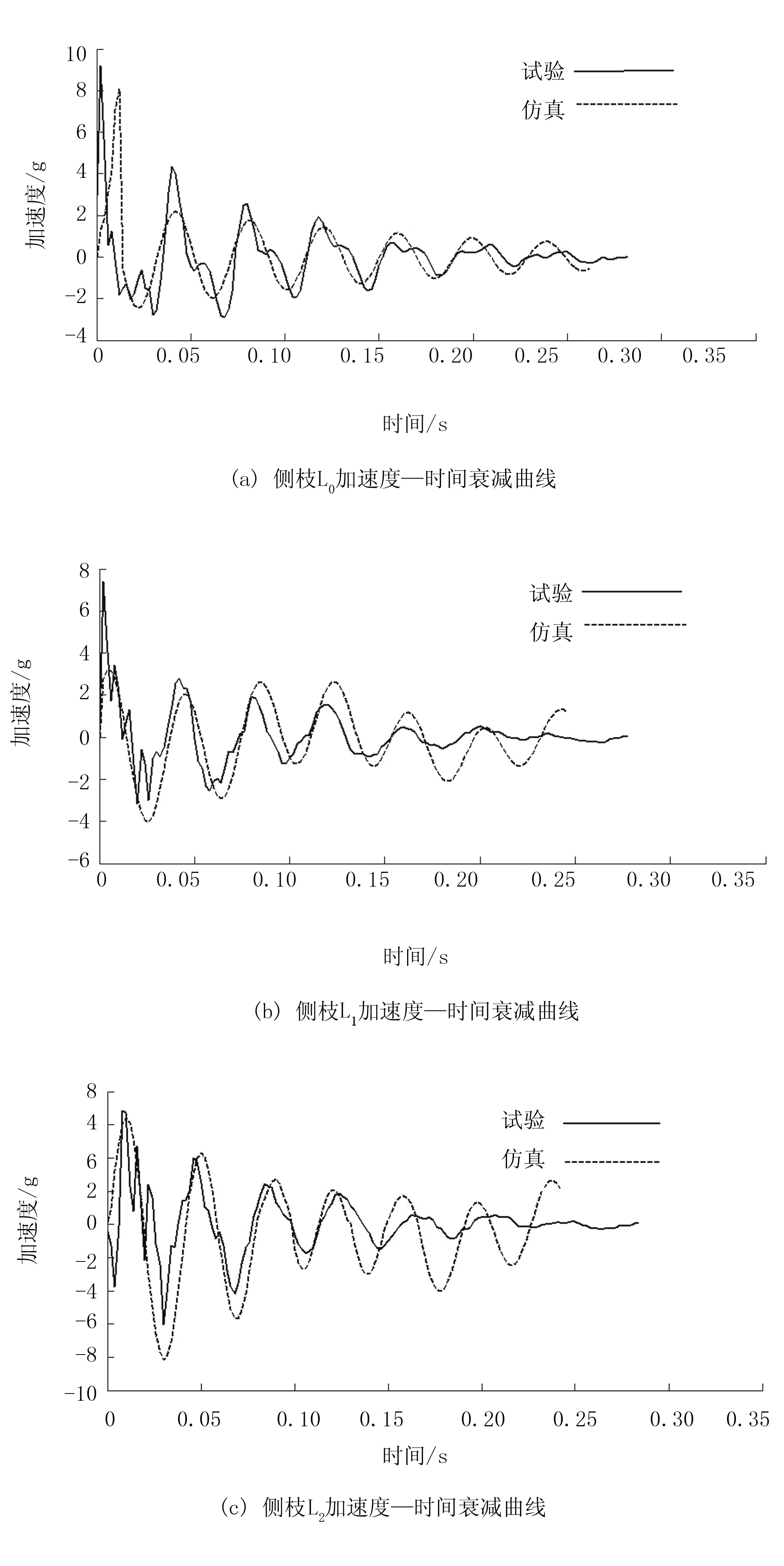
图10 9g载荷作用下试验与仿真曲线
将得到的仿真结果与试验结果进行比较,得出主干L0、主枝L1、侧枝L2的加速度时域变化曲线仿真与实验结果吻合程度较好。
2.5 果树共振频率
对采集到的加速度时域信号进行快速傅里叶变换(FFT)[15-16],得到各测点在不同激励信号作用下的加速度响应曲线,如图11所示。
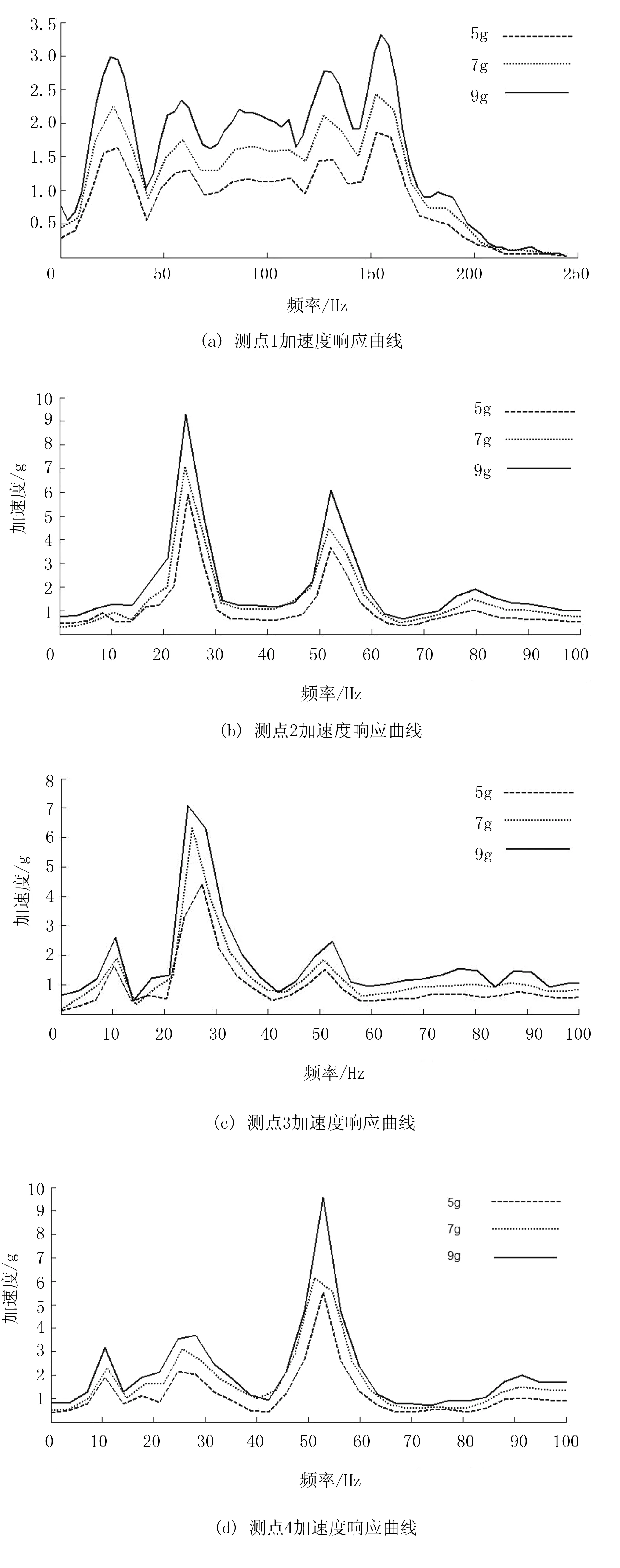

图11 各测点加速度响应
由各测点的加速度响应曲线可以看出:树干和树枝在25Hz左右产生共振,且共振峰较大;随着外界激振载荷的增大,树干和树枝所获得的加速度值也在不断增大,其数值增加的趋势与外界所施加载荷的大小近似成倍数增加,但共振频率并未发生改变。振动采收的基本原理是:外界激振载荷的能量通过树枝传递给果实,果实以某一加速度运动,使果实在运动过程中产生的惯性力大于果实与果柄间的结合力,从而使果实脱落。所以,在采收果实时,为提高采摘效率,使果实获得较大加速度,激振器的最佳激振频率应选择在25Hz附近,同时在不损伤果树的情况下,激振器激振载荷尽可能选择较大值。
3 结论
针对果树系统的复杂性及多样性所带来的建模困难问题,为使研究分析果树振动特性问题简化,提出用质量—弹性元件系统来建立果树力学模型的方法。为验证该方法的有效性,选择对“Y”型果树建立三自由度果树振动模型,即将主干L0、主枝L1、侧枝L2等效为3个质量块,并运用MatLab中Simulink子系统封装技术对所建立的振动模型进行仿真运算,将得到的仿真结果与试验结果进行比较,得出主干L0、主枝L1、侧枝L2的加速度时域变化曲线仿真与实验结果吻合程度较好,所建立的果树三自由度模型能够比较好地反映果树振动情况,所以用质量—弹性元件系统来建立果树力学模型是切实可行的。
同时,本文利用试验的方法对果树共振频率进行研究,得出树干和树枝在25Hz附近产生共振且峰值较大,所以在采集果实时激振器给定的最佳激振力频率应选择在25Hz附近。树干和树枝的加速度响应值随着激振载荷的增大而增大,因此在不损伤果树的情况下激振器的载荷应选择较大值。
[1] 梁勤安,楚耀辉.新疆特色水果机械化收获问题的探索[J].新疆农机化,2006(4):41-53.
[2] 陈都,杜小强.振动式果品收获技术机理分析及研究进展[J].农业工程学报,2011,27(8):195-200.
[3] Pacheco A,Rehkugler G E.Design and develop- ment of a spring activated impact shaker forapple harvesting[J].Transactions of the ASAE,1980,23(4):826-830.
[4] Kececioglu G. Research on olive harvesting possibilities with an inertia for tree shaker[D].Izmir:Ege University,1975.
[5] Yung C,Fridley R B.Simulation of vibration of forced vibrations of tree limbs with secondary branches[J].Transactions of the ASAE,1975,18(3):475-481.
[6] Castro-Garcia S,Blanco-Roldan G L,Gil-RibesJ A,et al.Dynamic analysis of olive trees in intensive orchards under forced vibration[J].Trees-structure and Function.2008,22(6):795-802.
[7] 郑甲红,毛俊超.振动式采摘机振动夹持位置的仿真研究[J].陕西科技大学学报,2014,32(1):142-147.
[8] 张敏敏.海棠果树粘弹性振动结构模型的研究[D].乌鲁木齐:新疆大学,2015.
[9] Zoltán Láng. A fruit tree stability model f-or static and dynamic loading[J]. BiosystemsEngineering, 2003,85 (4):461-466.
[10] Zoltán Láng. A simple model for fruit tree s-haking harvest[J].International Journal ofHorticultural Science,2007,13 (1):33-36.
[11] Zoltán Láng. A one degree of freedom damped fruit tree model[J].Transactions of the AS-ABE,2008,51(3): 823-829.
[12] 靳晓雄.汽车振动分析[M].上海:同济大学出版社,2002:27-29.
[13] 刘习军,贾启芬.工程振动理论与测试技术[M].北京:高等教育出版社,2004:33-34.
[14] 黎明安. MATLAB/Simulink动力学系统建模与仿真[M].北京:国防工业出版社,2012:27-36.
[15] 吴正毅.测试技术与测试信号处理[M].北京:清华大学出版社,1991.
[16] 王济. MATLAB在振动信号处理中的应用[M].北京:中国水利水电出版社,2006.Abstract ID:1003-188X(2017)08-0154-EA
"Y" Ttype of Fruit Tree Dynamic Model Simulation and Experimental Research
Liu Zilong, Wang Chunyao, Luo Jianqing,Wei Tingpeng, Lv Menglu
When we study the vibration characteristic of the fruit trees, in order to make the problem to simplify, this paper puts forward with a method to builed fruit tree mechanics model with quality - elastic element systemis .To verify the effectiveness of the method, we consider the "Y" fruit tree trunk L0, major branch L1, lateral branch L2as three mass piece to establish three degrees of freedom of fruit trees vibration model, and by using the Matlab Simulink subsystem in packaging technology to establish the vibration model of simulation calculation, the simulation results will be compared with the test results, it is concluded that the trunk L0, major branch L1, lateral branch L2acceleration curves of time domain simulation is consistent with the experimental results, the establishment of fruit trees three degree of freedom model can better reflect the fruit trees vibration situation, with quality-so elastic element system to establish the mechanical models of fruit tree method is feasible. Through the research on fruit resonant frequency around 25Hz determined to pick a more suitable excitation frequency, to provide the necessary theoretical basis for the optimization parameters fruit picking vibration harvester.
"Y" type of fruit trees; dynamic model; simulink; resonance frequency
2016-06-20
国家自然科学基金项目(51465054)
刘子龙(1991- ),男,山东潍坊人,硕士研究生, (E-mail)1104983216@qq.com。
王春耀(1956-),男,四川万源人,教授,硕士生导师,(E-mail) wangchun_yao@126.com。
S183
A
1003-188X(2017)08-0154-05
