基于启发策略的动态平衡图划分算法

李 琪 钟 将 李 雪

1(重庆大学计算机学院 重庆 400044) 2(昆士兰大学信息技术与电子工程学院 澳大利亚布里斯班 4072)

基于启发策略的动态平衡图划分算法

李 琪1钟 将1李 雪2

1(重庆大学计算机学院 重庆 400044)2(昆士兰大学信息技术与电子工程学院 澳大利亚布里斯班 4072)

(liqi0713@foxmail.com)

随着计算技术的发展以及大数据时代的来临，分布式计算已成为研究的热点，其中大图迭代计算作为其研究的重点，降低划分后子图之间的通信边规模是改善计算性能的关键.传统算法很难在切割率最小化与负载均衡上同时满足.由于图划分属于NP组合优化问题，提出了一种动态平衡算法来解决图的平衡划分，确保在子图边界点划分最优的基础上引入扰动策略使其跳出局部最优扩大搜索空间，最后在真实世界图上验证算法的可行性，分别从平衡系数、切割边规模与传统算法进行了比较.在指定的扰动次数下，此算法比常见的算法hash，Chunk，Metis在割边率上分别降低了近40%，30%，5%.与Metis相比，平衡系数也更加地优化，实验结果证明了该算法的有效性.

平衡图划分；启发策略；负载均衡；分布式计算；局部优化

给定一个无向图G=(V,E)，V和E分别表示顶点和边的集合，平衡K划分是把点集V按照映射关系π→(S1，S2，…，SK)映射到K(K≥2)个不相交的子域中，每个子域的规模几乎相等，要求使割边数最少(边的2个端点不在同一个域).当K=2时是2划分，针对2划分经典的是KL(Kernighan-Lin)[1]算法，其基本思想是将图随机划分为2等份，将2分结果作为输入，通过交换2个子域中的点来改进2分结果.此算法已经成为大多数图划分算法迭代改进的基础，但是由于其较高的时间复杂度O(|V|3)，不适合大图的直接处理.Fiduccia和Mattheyses[2]对其进行了改进，用单点移动来代替KL的双点交换以及加入了更有效的数据结构.图划分本身是NP完全问题[3],可以通过元启发式算法[4]解决此类问题，主要有模拟退火算法[5]、禁忌搜索算法[6]、遗传算法[7]等.另外，Kumar等人提出了多层次的图划分模型Metis[8]和它的并行版本ParMetis[9].Metis算法设计主要基于多层次图划分范式.此类方法还包括Chaco[10]和Scotch[11].图划分有广泛的应用，例如并行计算[12]、VLSI设计[13]、图像分割[14]等.

图可以表达复杂的结构和丰富的语意，其迭代分析算法在社交网络、Web和科学计算等诸多领域获得了广泛的应用[15],然而，随着数据规模的不断增长对计算要求提出了严峻的挑战.在2012年，Google月活跃用户数为10亿，Twitter月活跃用户数为2亿，平均每天发送的消息量达到了1.75亿，与之相对应的是数十亿的边与顶点，但是我们仍要通过这些庞大的图数据来进行一些相关的计算，例如PageRank、寻找连通分量、计算三角形等.将如此海量的图数据存储在单机环境中计算效率会非常的低，进而人们开发了分布式迭代处理系统，如Pregel[16],GraphLab[17]，Spark[18]，Giraph[19].图划分是Spark等系统进行分布式计算的提前，每次迭代处理均会引入巨大的通信开销，这将成为制约分布式处理性能的关键因素.一个良好的划分算法应保证划分后的子图在负载均衡的前提下，最小化割边数规模.因此，设计划分效果优越的图分割算法已经成为现有大图处理系统急需解决的问题，已有的图划分算法[20-21]在割边数规模与子域负载平衡上难以同时满足.针对此问题，本文提出了动态平衡图划分算法——DyBGP，利用多种策略确保各子域负载均衡的基础上最小化割边率.

本文的贡献主要有2个方面：

1) 设计了基于启发策略的动态平衡图划分算法，贪心顶点转移操作能够有效地减少割边数达到局部最优，分区容量限制策略用来平衡各子域的负载，又定义了扰动策略，是跳出局部最优的关键，并利用全局记忆结构存储最优的结果，同时也对该算法的复杂性进行了理论分析；

2) 在真实的图数据上进行实验分析，分别在切割边数量与平衡度2方面分别与Hash，Chunk，Metis进行比较，实验结果证明了本文所提出算法在平衡图划分问题的有效性.

1 图划分及符号定义

1) 图划分.给定一个无向图G=(V,E),V和E分别表示图的点集和边集，K路平衡划分是将顶点V按照某种策略分配到K个子域中S1,S2,…,Sk,要求在各子域负载平衡的基础上最小化割边率，Vi代表第i子区中的顶点集，V1∪V2∪…∪Vk=V,Vi∩Vj=∅，i≠j，ρ为平衡系数(ρ≥1),理想值为1.0.图划分问题可以定义为

(1)

(2)

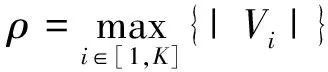
(3)

式(2)中的ECutij为子域Si到Sj(或者Sj到Si)所有边的集合(Si≠Sj).

2)g(v,n).点v从所在子域Slocal移向另一个子域Sj(Slocal≠Sj),割边减少的数量我们称之为收益值，|EVi|(i∈[1,K])表示子域Si中点与点v相连的边数，图1中有4个子域(S1,S2,S3,S4),点v在子域S3(Slocal)中，|EV1|=3,|EV2|=1,|EV3|=2,|EV4|=2.

n代表点v所移动的目标子域，取获得收益最大的子域，g(v,n)不仅有正值也有负值(图1中g(v,1)=1)，用数学形式表示g(v,n)为

(4)

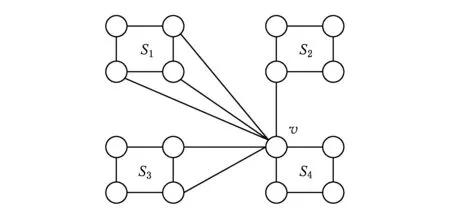
Fig. 1 An example of 4-partitioning图1 4个子域的图划分

2 动态平衡图划分算法

当初始划分完成后，首先选取边界点作为候选点，然后定义多种策略确保图的候选点划分(割边数规模、子域负载)达到最优，为了扩大搜索范围我们加入了扰动策略，在此基础上引入了惩罚措施，惩罚负载过大和过小的子域，算法1用伪代码详细描述了此过程，详细的子过程将分别在2.1～2.3节、2.5节介绍.

算法1. 动态平衡划分算法(DyBGP).

输入：初始划分Pk={V1,V2,…,VK}(见2.1节)；

输出：划分结果.

步骤1. 初始化参数，扰动次数(pertur_times),禁忌列表(tabu list),全局记忆结构(global memory structure)；

步骤2. For每一个候选点

计算g(v,n)；

将点v插入增益结构(见2.2节)；

End For

步骤3. Whilepertur_times

计算此时划分图状态；

① If 收敛

执行扰动策略跳出局部最优；

pertur_times=pertur_times-1；

pertur(v,n)(见2.5节)；

更新增益结构和全局记忆结构；

② Else If 没有收敛

Repeat

iter_number=iter_number+1；

greedy_move(v,Sdst)(见2.3节)；

更新增益结构和禁忌列表；

Balance_move(v,Sdst)(见2.3节)；

更新增益结构和禁忌列表；

Until候选点的收益值都小于等于零

③ 执行惩罚策略(见2.5节)；

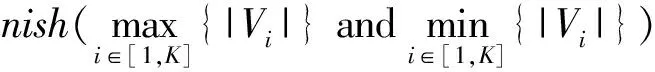
End If

End While

2.1 初始划分

首先将图分为K个小图，为了证明本算法是否与初始划分有关，本文列出了3种初始的图划分.

1) Hash.Pregel,GraphLab采用此方法，根据index=Hash(ID) modK将顶点映射到第index个分区，K为分区数.此方法时间复杂度很低O(V).

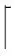
3) Metis.Metis属于多级划分，分为3个阶段——粗化、划分、细化.粗化阶段是压缩图的规模，时间复杂度大于O(|E|);粗化后的图用KL等算法进行划分，时间复杂度为O(N3)，N为粗化后的顶点数，细化是将图恢复成原图并且在恢复过程中不断调整优化，时间复杂度大于O(|E|);Metis划分整个过程时间复杂度大于O(2×|E|+N3).

2.2 增益结构

桶结构首次被Fiduccia和Mattheyses提出[2]，是为了改进2划分的KL算法，把所有相同收益值的点放在木桶结构中的相同位置，根据收益的大小进行移动操作，时间复杂度明显降低.Benlic等人[22]提出了针对K-划分的木桶结构.但是其随着子域数量的增加，所消耗的内存也是急速地增加，本文也提出了针对本算法的结构.

首先计算候选点的收益值，将点插入到对应的收益值列表中，对应相应的目标子域，每次将最大收益值对应的点移向目标子域.另外，还增加了邻居列表和邻居所在列表位置的列表，当点v发生移动时，我们只需要根据索引更新点v和点v周围邻居点的值，每次更新所需要的时间复杂度与点v的邻居数有直接的关系，同样也大大减少了计算量.图2举例说明了将例图划分为3个子图的增益结构.

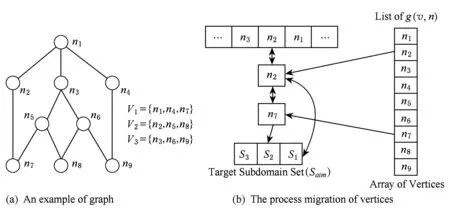
Fig. 2 An example of gain struct for 3-partitioing图2 例图划分为3个子域的增益结构

2.3 局部优化策略

为了在候选点上执行局部优化操作，采用的操作策略:

如果移动之前|Vsrc|<|Vdst|,那么移动之后在子域Sdst选择某一点v，满足g(v,Ssrc)≥0,移向目标子域Ssrc.但是如果对于Sdst中任意的点收益值g(v,Ssrc)<0,则不移动.

2) 子域负载限制操作{balance_move(v,Sdst)}.对于同一个子域来说，每次迭代可能会有很多点从不同子域转移过来，造成子域负载不平衡,因此设计了一种平衡操作，这种操作规定任意选择2个子域Si和Sj,如果|Vi|>|Vj|,在子域Si中，选择某一点v且g(v,Sj)≥0,将点v从Si移向Sj(如果|Vi|<|Vj|,执行相反的操作),此操作也可以进一步降低割边率.

2.4 禁忌列表和全局记忆结构管理

1) 禁忌列表(tabu list).本文所采用的转移决策具有独立性，局部的对称性会导致无效的转移，如1对互为邻居的顶点，在迭代中2顶点可能相互转移到对方所在的子域中不断地互相多次转移，影响局部的收敛，为了防止此类无效的转移，规定：当某个顶点从Si转移到另一个子域Sj，在某个常数时间内禁止返回原子域.该算法增加了禁忌表tabu list，禁忌长度定义为t(v,Si)=border(|Vi|)×α,border(|Vi|)表示子域Si的边界点个数，α是一个因子，在本文中设α=0.05，每次扰动之前，tabu list将清空重新计算.

2) 全局记忆结构(global memory structure).由于扰动具有随机性，因此，在设定的扰动次数下，用全局记忆结构存储划分效果最好的一次扰动，但是也会相应的增加内存消耗.

2.5 扰动和惩罚策略

为了跳出局部最优，本文设计了一种扰动策略，选择一个子域Si，在Si中任意选择其中的γ个内点(边界点之外的点)，每个点任意地移向其他子域Sj(Si≠Sj)，γ=0.03×inside(|Vi|).点在不断的移动过程中，有些子域负载规模可能过大或过小，因此，引出2种惩罚措施.

以上2种策略，都是在收益值大于或等于零的情况下进行移动，因此不会增加图的割边率.

2.6 复杂度分析

本节对所提出算法的复杂度进行分析，本算法的复杂度主要体现在初始划分、扰动以及扰动之后的迭代时间，由于初始划分的随机性，因此设初始划分的复杂度为O(t).扰动次数为pertur_times，每轮扰动之后的迭代次数为iter_number，扰动之后总的迭代时间为pertur_times×iter_number.本文中每次扰动的顶点数为0.03×inside(|Vi|)，因此扰动需要的时间复杂度为pertur_times×0.03×inside(|Vi|).整个算法时间复杂度O(t+pertur_times×iter_number+pertur_times×0.03×inside(|Vi|).

3 实 验

本节我们在真实图上来测试本算法的可行性，介绍实验的具体步骤及平台环境，展示实验的结果并对这些结果进行分析.

3.1 实验方案与环境

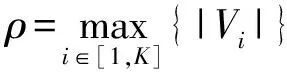
实验中使用的真实图数据来源于斯坦福大学网络分析项目,详细图信息在表1中.算法用python语言编写，在AMD phenom Ⅱ X4 955 4 GB上编译测试.

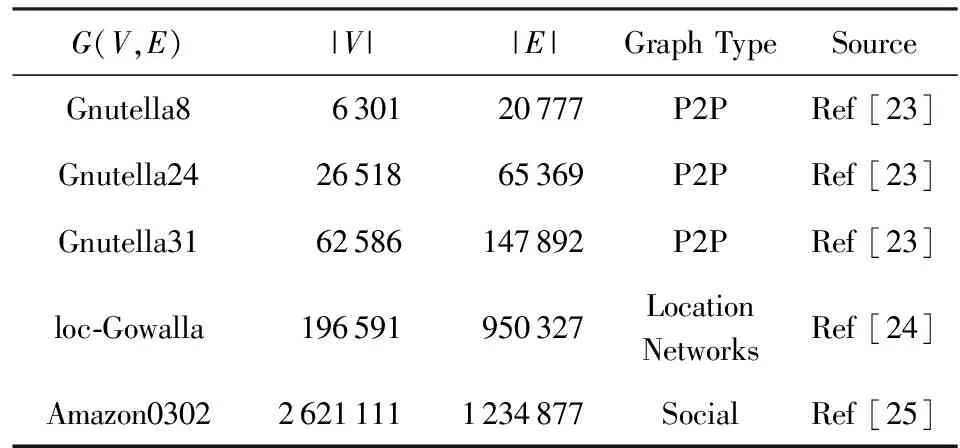
Table 1 Experimental Data Sets表1 实验数据集

3.2 实验结果与分析

如图3所示，我们用Hash，Chunk，Metis方法分别对图loc-Gowalla进行了初始的K-划分(K=2,6,8,16,32,64)，由图3可以看出Hash的划分结果最差，当子域数量为64时割边率几乎达到了94%;Metis的划分效果明显优于Hash和Chunk，随着子域的增多，割边比也会增加，但增幅明显小于Hash与Chunk.

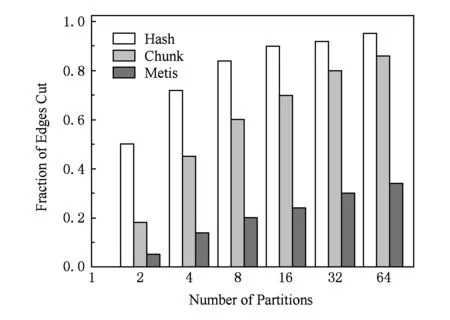
Fig. 3 Results of initial partitioning on loc-Gowalla图3 基于Hash，Chunk，Metis的K-划分

扰动策略是跳出局部最优的关键，因此也对扰动策略进行了实验分析，在图4中，在没有扰动策略的情况下(即算法1中没有步骤①)割边率与迭代次数(iter_number)的关系，横坐标为迭代次数，纵坐标为割边率.图5展示了加入扰动策略之后扰动轮数与割边率的关系，横坐标为扰动次数(dister_number)，纵坐标为割边率.

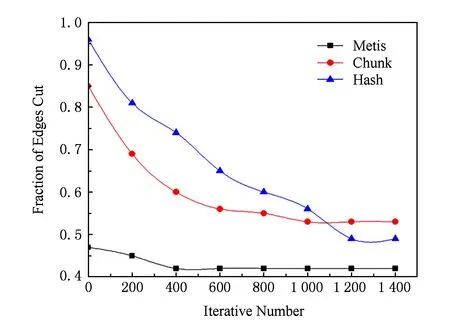
Fig. 4 Results of 16-partitioning on p2p-Gnutella8 without perturbation strategy图4 p2p-Gnutella8上没有扰动策略的16-划分结果

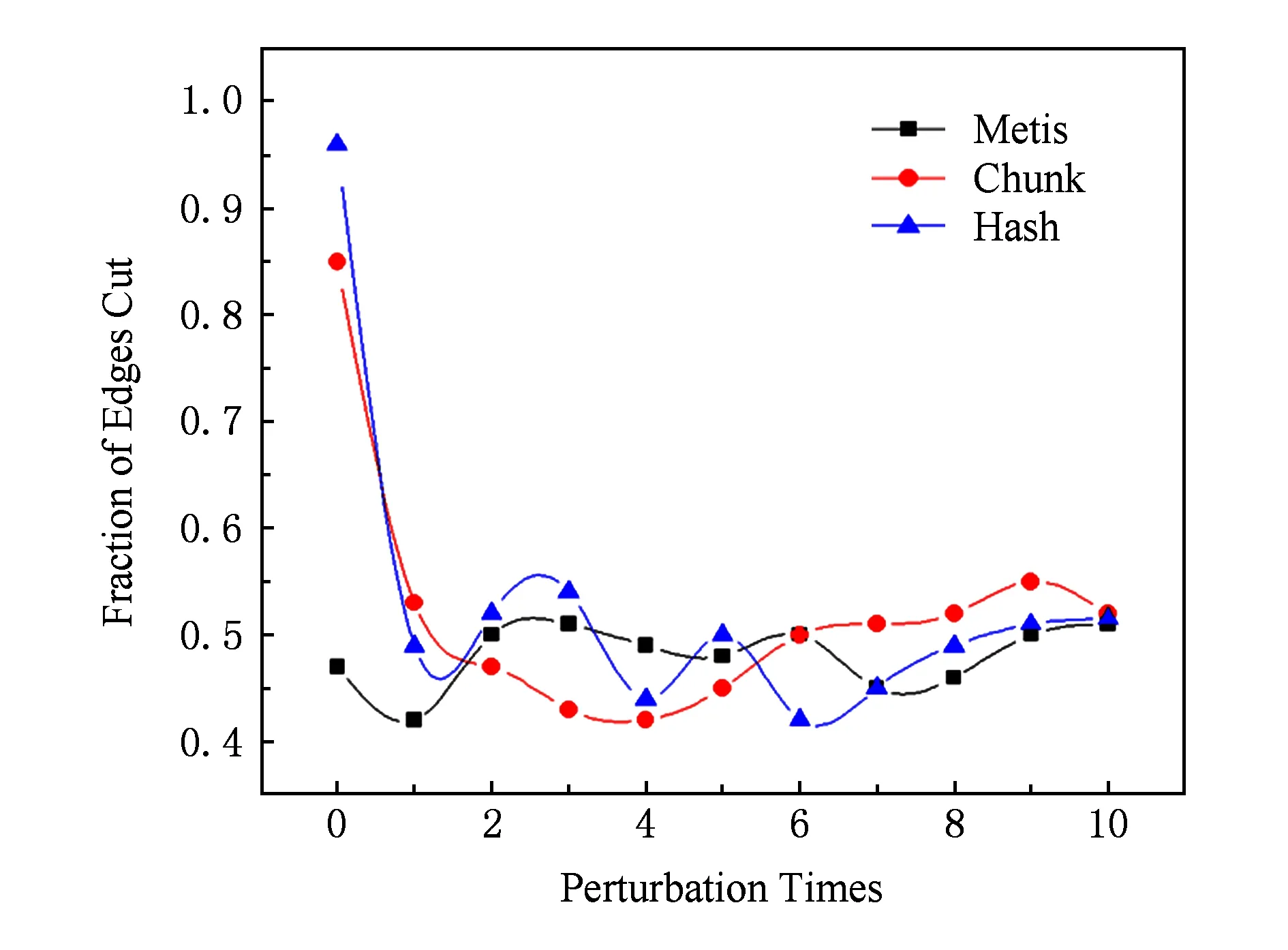
Fig. 5 Results of 16-partitioning on p2p-Gnutella8 with perturbation strategy图5 p2p-Gnutella8上加入扰动策略的16-划分结果

如图4所示，由于Hash的初始划分的割边率明显高于Chunk和Metis，在没有扰动的情况下，Hash迭代收敛的次数最高，Metis收敛的迭代次数最少.加入扰动之后，如图5所示,割边率都会有进一步降低，随着扰动次数的增加，全局记性结构里都会存储最好的划分结果，由结果可以看出，划分结果质量的优劣与初始划分没有关系.

最后在表2中，分别取Hash，Chunk，Metis为本算法的初始划分，结果取其平均值作为提出算法的划分结果,括号中的数值为平衡因子.从表2中，可以看出DyBGP算法在割边率上明显提高，而且在平衡度上与Metis相比也有所提升，证明了所提出算法的有效性.

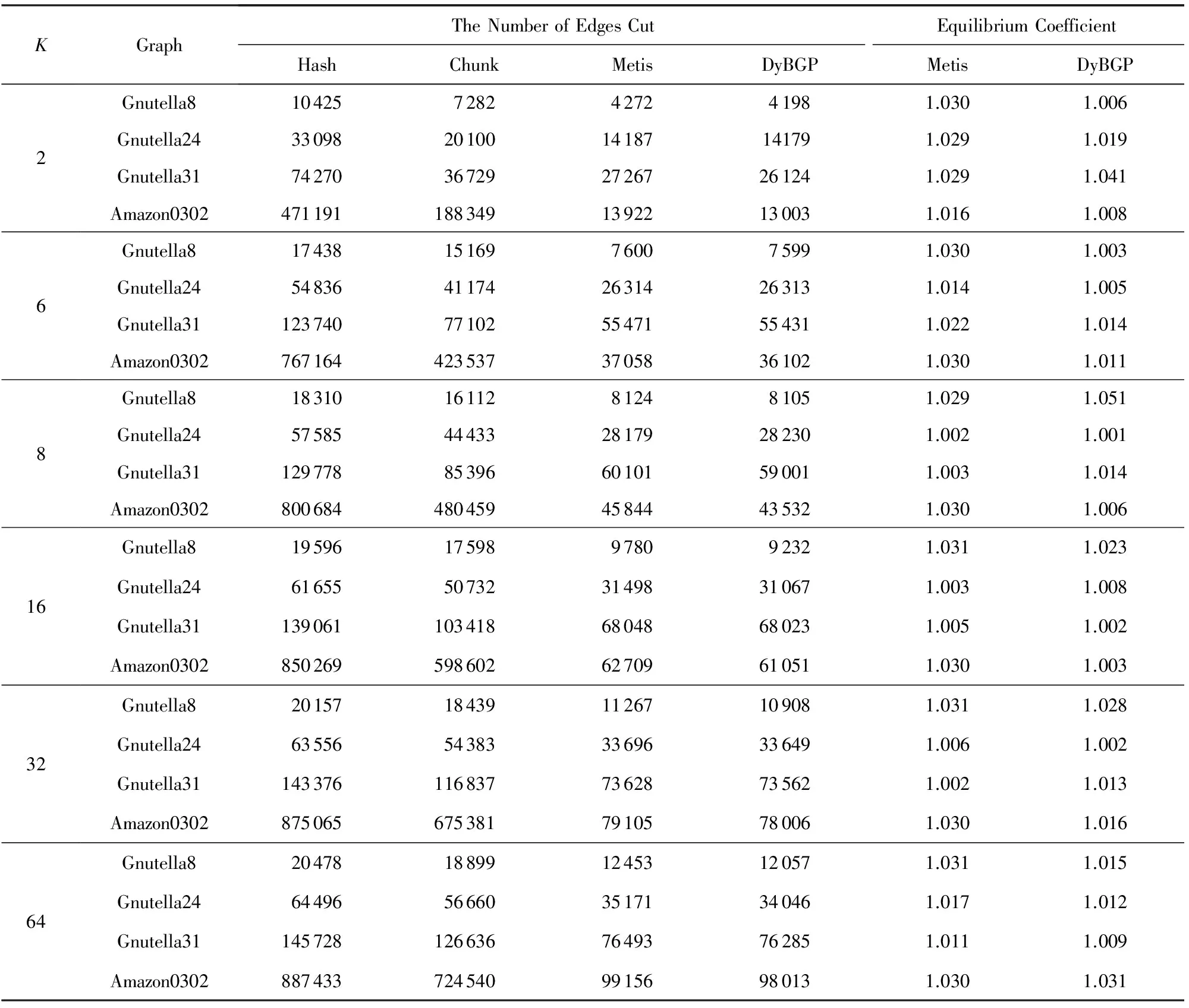
Table 2 Comparion of Our Approach (DyBGP) with Hash, Chunk and Metis表2 本文提出的方法(DyBGP)与Hash，Chunk，Metis结果比较

4 结论与未来工作

本文利用初始划分的局部信息(边界点)通过启发式策略调整点位置达到局部最优，为了扩大搜索范围，我们又定义了扰动策略，用多种策略来确保图的平衡划分且最小化割边率，实验数据也证明了此算法的有效性.平衡图划分有着广泛的应用，随着大数据发展与应用，在图并行框架中起着重要的作用，未来，我们将图划分运用到具体的大图迭代系统中，与具体的计算相结合，对于后续大图算法的研究有很重要的意义.

[1]Dutt S. New faster kernighan-lin-type graph-partitioning algorithms[C] //Pro of ICCAD-93. Piscataway, NJ: IEEE, 1993: 370-377

[2] Fiduccia C M, Mattheyses R M. A linear-time heuristic for improving network partitions[C] //Proc of the 19th IEEE Conf on Electronic Design Automation. New York: ACM, 1988: 241-247

[3] Garey M R, Johnson D S, Stockmeyer L. Some simplified NP-complete graph problems[J]. Theoretical Computer Science, 1976, 1(3): 237-267

[4] Xu Jinfeng, Dong Yihong, Wang Shiyi. Summary of large-scale graph partitioning algorithms[J]. Telecommunications Science, 2014, 30(7): 100-106 (in Chinese)(许金凤, 董一鸿, 王诗懿. 大规模图数据划分算法综述[J]. 电信科学, 2014, 30(7): 100-106)

[5] Johnson D S, Aragon C R, McGeoch L A. Optimization by simulated annealing: An experimental evaluation; part I, graph partitioning[J]. Operations Research, 1989, 37(6): 865-892

[6] Rolland E, Pirkul H, Glover F. Tabu search for graph partitioning[J]. Annals of Operations Research, 1996, 63(2): 209-232

[7] Rahimian F, Payberah A H, Girdzijauskas S, et al. JA-BE-JA: A distributed algorithm for balanced graph partitioning[C] //Proc of the 7th IEEE Int Conf on Self-Adaptive and Self-Organizing Systems. Piscataway, NJ: IEEE, 2013: 51-60

[8] Karypis G, Kumar V. A fast and high quality multilevel scheme for partitioning irregular graphs[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 359-392

[9] Karypis G, Schloegel K, Kumar V. Parmetis: Parallel graph partitioning and sparse matrix ordering library[OL]. [2016-08-16]. https://www.research-gate.net/publication/238705993_Parmetis_Parallel_graph_partitioning_and_sparse_matrix_ordering_library

[10] Hendrickson B, Leland R. A multi-level algorithm for partitioning graphs[C] //Proc of ACM/IEEE Conf on Supercomputing. New York: ACM, 1995: 28-28

[11] Pellegrini F, Roman J. Scotch: A software package for static mapping by dual recursive bipartitioning of process and architecture graphs[C] //Proc of HPCN-Europe 1996. Berlin: Springer, 1996: 493-498

[12] Simon H D. Partitioning of unstructured problems for parallel processing[J]. Computing Systems in Engineering, 1991, 2(2/3): 135-148

[13] Karypis G, Kumar V. Multilevelk-way partitioning scheme for irregular graphs[J]. Journal of Parallel and Distributed Computing, 1998, 48(1): 96-129

[14] Grady L, Schwartz E L. Isoperimetric graph partitioning for image segmentation[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 2006, 28(3): 469-475

[15] Chen Ling, Li Xue, et al. Mining health examination records—A graph-based approach[J]. IEEE Trans on Knowledge and Data Engineering, 2016, 28(9): 2423-2437

[16] Malewicz G, Austern M H, Bik A J C, et al. Pregel: A system for large-scale graph processing[C] //Proc of the 2010 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2010: 135-146

[17] Low Y, Bickson D, Gonzalez J, et al. Distributed graphLab: A framework for machine learning and data mining in the cloud[J]. Proceedings of the VLDB Endowment, 2012, 5(8): 716-727

[18] Zaharia M, Chowdhury N M, Franklin M J, et al. Spark: Cluster computing with working sets[C] //Proc of the 2nd USENIX Conf on Hot Topics in Cloud Computing. Berkeley, CA: USENIX Association, 2010: 10

[19] Avery C. Giraph: Large-scale graph processing infrastructure on hadoop[OL]. [2016-08-16]. http://giraph.apache.org/

[20] Stanton I, Kliot G. Streaming graph partitioning for large distributed graphs[C] //Proc of the 18th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2012: 1222-1230

[21] Mehrdoost Z, Bahrainian S S. A multilevel tabu search algorithm for balanced partitioning of unstructured grids[J]. International Journal for Numerical Methods in Engineering, 2016, 105(9): 678-692

[22] Benlic U, Hao J K. An effective multilevel tabu search approach for balanced graph partitioning[J]. Computers & Operations Research, 2011, 38(7): 1066-1075

[23] Leskovec J, Kleinberg J, Faloutsos C. Graph evolution: Densification and shrinking diameters[J]. ACM Trans on Knowledge Discovery from Data, 2007, 1(1): 2

[24] Cho E, Myers S A, Leskovec J. Friendship and mobility: User movement in location-based social networks[C] //Proc of the 17th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2011: 1082-1090

[25] Leskovec J, Adamic L A, Huberman B A. The dynamics of viral marketing[J]. ACM Trans on the Web, 2007, 1(1): 228-237

DyBGP:ADynamic-BalancedAlgorithmforGraphPartitioningBasedonHeuristicStrategies

Li Qi1, Zhong Jiang1, and Li Xue2

1(CollegeofComputerScience,ChongqingUniversity,Chongqing400044)2(SchoolofInformationTechnologyandElectricalEngineering,UniversityofQueensland,Brisbane,Australia4072)

With the development of computing technology and the advent of the era of big data, the distributed computing has became a research hotspot. Iterative computation of big graph becomes the focus of the research. Reducing the communication data quantity between subgraph after effective partitioning, it is the key to improve the computational performance, because the existing algorithms are difficult to meet the requirements on both minimizing fraction of egdes cut and load balancing at the same time. In this paper, a dynamic-balanced algorithm for graph partitioning named DyBGP is proposed, and it is used to solve the problem of balanced partition. Based on ensuring the partitioning of subgraph boundary vertices optimal, the perturbation strategy to jump out of local optimum to expand the search space is used. Finally, our algorithm is verified the feasibility in the real-world graph, respectively from the balance coefficient and the scale of edges cut compared with the traditional algorithms, such as Hash, Chunk and Metis. In the number of edges cut, it is decreased about 40%, 30%, 5% with our algorithm under specifying perturbation times. In the balance coefficient, our algorithm is more optimized than Metis. The experimental results show that the algorithm is effective.

balanced graph partitioning; heuristic strategies; load balancing; distributed computing; local optimization

his PhD from Queensland University of Technology in 1997. His main research interests include opinion analysis from social media, big data analytics, knowledge discovery from sequences, mining distributed, high-speed, time-variant data streams, etc.

2016-09-09；

2017-02-21

国家“八六三”高技术研究发展计划基金项目(2015AA015308)；重庆市社会事业与民生保障科技创新专项(cstc2017shmsA0641)

This work was supported by the National High Technology Research and Development Program of China (863 Program) (2015AA015308) and the Social Undertakings and Livelihood Security Science and Technology Innovation Funds of CQ CSTC (cstc2017shmsA0641).

钟将(zhongjiang@cqu.edu.cn)

TP301.6

LiQi, born in 1987. PhD candidate at the College of Computer Science, Chongqing University. His main research interests include data mining and graph computing, etc.

ZhongJiang, born in 1974. Recevied his PhD degree in computer science from Chongqing University in 2005. Professor and PhD supervisor. His main research interests include data mining, management information system, trusted computer system, service computing, etc.