一种基于全相位预处理有效消除图像Gibbs伪迹的方法

2017-12-15褚晶辉王晓娜黄翔东

数据采集与处理 2017年5期

关键词：伪影傅里叶表达式

褚晶辉王晓娜黄翔东吕卫

(天津大学电子信息工程学院,天津,300072)

一种基于全相位预处理有效消除图像Gibbs伪迹的方法

褚晶辉王晓娜黄翔东吕卫

(天津大学电子信息工程学院,天津,300072)

经典傅氏重构是一种重要的信号处理方法，该方法对连续信号重构有很好的效果，但对有间断点的信号进行重构时就会产生Gibbs效应。Gibbs现象的存在使得重构信号在边缘处存在较大的失真，严重影响了图像质量。为此，提出了改进的二维全相位重构方法，在给定有限个离散傅里叶(Discrete fourier transform,DFT)系数的情况下，综合了更多的高次谐波信息，从而实现了高精度的重构间断信号。将该算法应用于重构磁共振成像(Magnetic resonance imaging,MRI)图像的实验结果表明：相比于传统的傅里叶变换法，该重构算法可在不增加傅里叶系数的条件下同时有效减小图像的Gibbs效应，改善了重构图像的质量。

经典傅氏重构; 磁共振成像; Gibbs效应;全相位

引言

傅氏重构是一种非常重要的信号处理工具，特别是在信号重构领域有着广泛的应用。用傅里叶近似去重构原始图像，当图像没有间断时，傅里叶逼近能一致收敛于原始图像。然而，如果图像不连续，在原来信号不连续点处的重建会出现寄生振荡和整体收敛速度大大减小的现象，这就是著名的Gibbs效应[1-3]。

传统的消除Gibbs伪迹的方法是对原始数据进行滤波，削弱高频信息来达到消除Gibbs伪迹的目的，但同时会引起重建图像的边缘模糊，而且在边缘附近仍存有伪迹[4]。另外也有通过小波扩张的方法来消除Gibbs伪迹，该方法能够较好地去除Gibbs伪迹，但是计算量较大，难以用于工程实现[5,6]。在只有部分傅里叶系数情况下，为了实现原始信号的精确重构，通常采用全相位傅式法[7]这一新的重构间断信号方法。该方法在给定有限个(Discrete Fourier transform,DFT)系数的情况下，采用循环移位的方式对频域数据进行处理，综合了更多的高次谐波信息，从而实现了高精度的重构间断信号。原来的研究只针对一维间断信号进行重构[8]，本文将该方法成功推广到二维，首先介绍了全相位一维信号重构理论，在此基础上提出了改进的二维全相位重构方法，最后通过两组仿真实验来验证该方法，并对实验结果进行了对比分析。

1 全相位一维信号重构理论

用重叠的方式处理信号截断问题一直是国内外许多学者所持有的观点[9]，而全相位思想就是一种最大程度重叠的信号处理方式。它考虑了频域数据所有可能的分段情况，处理得到扩展后的频域数据相当于给原始信号补充了高频成分，从而在不降低重构图像空间分辨率的情况下，达到减小图像边缘的Gibbs效应的目的。

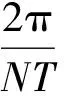
(1)

那么，傅里叶重构表达式为

(2)

式(1)中0≤k≤N-1，现在，将k的范围扩展为-N+1≤k≤N-1，根据DFT的循环移位性质可以很容易证明Fk=Fk+N,k=-N+1,…,-1。和式(2)类似，可以得到N个子重构的表达式为

(3)

对N个子重构求平均可以得到全相位重构的表达式为

(4)

全相位重构的过程如图1所示，包括3个步骤：(1) 将重构系数Fk循环右移；(2) 将扩展后的系数Fk配以更高的谐波分量ejkw0t；(3) 将所有移位后的DFT系数的子重构fi(t)叠加起来求平均。

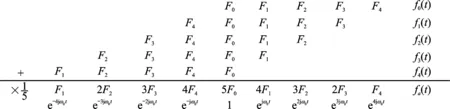
图1 N=5时全相位预处理过程Fig.1 Pre-processing of Fourier coefficients N=5

比较式(2,4)可以发现，数值上全相位重构是所有子重构的求和平均。这种未对各个子重构单独加窗的方式被称为无窗全相位傅里叶重构。

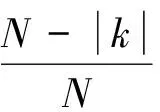
(5)

则ωk可表示为

(6)

为了进一步改善逼近效果，可对各个子重构fi(t)用中心对称的N阶窗h(k)加窗处理，则式(3)中的子重构可改写为

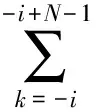
(7)

此时权重函数ωk[8]为

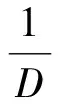
(8)

式中D为归一化因子，它能保证ωk的中心元素为1，其值为

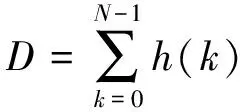
(9)

不同的窗函数效果不同，本文采用最常用的汉明窗来处理各个子重构系数，因此式(9)中的h(k)可表示为

(10)

2 基于全相位预处理的二维傅里叶重建法

通过前文可知，一维情况下直接对数据进行循环移位再叠加就可以得到扩展后的频域系数。因为二维傅里叶变换具有可分离的特性，因此可以把该重构方法推广到二维，用来重构含有间断点的二维信号，比较典型的如磁共振成像(Magnetic resonance imaging,MRI)图像。

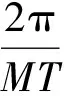
(11)

那么，传统傅里叶重构表达式为

(12)

对于上述DFT系数矩阵{Fk,l}，基于全相位预处理的二维重构算法流程为：(1) 将DFT系数矩阵{Fk,l}依次在行方向和列方向进行循环移位，得到扩展系数矩阵{Fk′,l/}；(2) 用窗函数Wk′和Wl′分别对{Fk/,l′}在行和列两个方向进行加权；(3) 采用全相位预处理后的频域数据进行傅里叶级数重构。

根据算法步骤(1)，可以得出，经过循环移位扩展后的频域系数{Fk′,l′}的表达式为

(13)

式中k′=-M+1,…,0,…,M-1;l′=-N+1,…,0,…,N-1；显然，扩展后的系数矩阵{Fk′,l′}大小为(2M+1)×(2N+1)，这表明用于重构的频域数据量增加了，这是合成的高频成份对原始DFT系数矩阵进行补充的结果。

算法流程(2)中对DFT系数矩阵{Fk,l}在行和列两个方向上加权的权重函数的表达式为

(14)

综合式(13,14)，采用傅里叶级数重构的方式，可得到二维全相位重构的表达式，即

(15)

基于全相位预处理的二维重构算法在对{Fk,l}处理过程中实际可以得到M×N组频域数据，对这些数据分别配以相应的谐波分量去单独重构，就可得到M×N个子重构的表达式，即

(16)

因此二维全相位重构也可以表示为

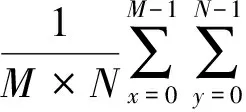
(17)

在式(16)中，如果x=y=0，就意味着没有对DFT系数矩阵进行循环移位，则f0,0(t1,t2)为传统的傅里叶重建。从数值上来看，二维全相位重构为M×N路子重构的求和平均，由于没有对各个子重构进行单独的加窗处理，因此被称为不加窗的二维全相位重构。

参照一维情况的处理方式，在行方向引入一个长为M的中心对称矩形窗RM，在列方向引入一个长为N的中心对称矩形窗RN，则Wk′和Wl′可表示为

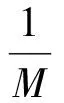
(18)

为了进一步改善逼近效果，优化重建图像的质量，可以对子重构进行加窗。根据全相位二维重建的算法流程，结合一维情况下的加窗处理，可以得到，二维情况下的卷积窗等效于两个方向的卷积窗的乘积，因此可从两个方向对子重构进行加窗：(1) 用长度为N的窗序列hN对原始数据在水平方向进行加权；(2) 将加窗后的数据矢量逐个简单循环右移，并将得到的N组新数据矩阵以中心向量为基准进行对齐，在竖直方向上进行叠加求和后得到二维矩阵F；(3) 对F在竖直方向用长度为M的窗序列hM加权；(4) 将加权后的M组数据在竖直方向逐个简单循环移位，并在竖直方向上分别进行中心对齐后进行求和叠加，就得到了单窗全相位输入序列。

通过以上分析，可以推出，在加窗情况下，二维全相位重构的表达式并没有改变，只是卷积窗的形式发生了变化。可以得到，单窗二维全相位情况下的卷积窗表达式为

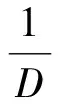
(19)

相比于单窗全相位数据预处理，双窗全相位预处理只是在数据进行中心对齐叠加时用一个窗序列进行加权求和，其全相位重构的表达式并没有改变，只是卷积窗的形式发生了改变。双窗二维全相位情况下的卷积窗表达式为

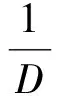
(20)

式中：hk为汉明窗。

3 仿真实验与结果分析

在Matlab环境下，通过两组仿真实验来验证所提的方法。一组为典型的二维方波信号的重构；另一组为本文算法的一个典型应用，即MRI图像的重构。

3.1 二维方波信号的重建

本组实验选用常见的方波信号进行重构，并与经典的傅氏重构结果进行比较，以验证本文所提算法的有效性，图2给出了其实验结果。通过对如图2(a)所示的原始方波进行128×128采样得到其DFT系数，将选取其中心的部分傅里叶系数进行重构。图2(b)为有限个(N=39)DFT系数作傅里叶级数重构，可以看出，在信号不连续点处存在很明显的Gibbs效应。图2(c，d)为本文所提算法的重建结果，其中图2(c)是无窗的全相位重构，图2(d)是加汉明窗重构的结果，可以看出，基于全相位预处理重构的信号Gibbs效应得到了很明显的改善，并且加窗全相位比无窗全相位的效果好。实验证明了基于全相位预处理的二维傅里叶重构算法的有效性。

3.2 MRI重建

MRI 图像的重构是傅里叶算法在二维图像重构领域的典型应用。在临床的磁共振成像中，一般采用减小数据采集量，即部分K 空间傅里叶成像技术来缩短所需的扫描时间，进而解决成像时间较长的问题。然而由于 K 空间数据的有限采样[10]，重构图像中经常出现较严重的Gibbs 伪影。为了比较本文提出的方法与传统傅里叶方法在抑制Gibbs伪影方面的效果，本组实验对MRI图像重建进行了仿真，实验数据为通过256×256的 Sheep-Logan 脑部模型进行二维傅里叶变换得到的原始K空间数据。由于K空间数据具有对称性，选取中心大小65×65的部分K空间数据作为原始频域数据，对其进行直接填零重建作为参照。

图3(a)是采用部分K空间数据，用傅里叶级数方式重构得到的MRI图像，可以看到图像包含明显的Gibbs伪影，具体表现为图像边界附近明暗相间的条纹，并且越靠近边界的地方越明显。图3(b，c，d)为采用基于全相位预处理的二维傅里叶重构算法得到的MRI图像，其中图3(b)为不加窗的形式。可以看到，虽然Gibbs 伪影得到了明显的改善，但在边界处仍存在着明暗相间的环状伪影；图3(c,d)分别为单窗和双窗重建的结果，可以看出，边界的 Gibbs 伪影几乎完全消除，并且图像的边缘保持了很高的分辨率，细节部分表现很好。由此可见，本文提出的算法可以有效地抑制Gibbs伪影，且在加窗之后取得更好的抑制效果。图3(e-h)分别是图3(a-d)的横截面图(第100行)，从截面图中，可以更直观地看到Gibbs 伪影的表现情况：图3(e)是傅里叶级数重构得到的截面波形图，可以看到其过渡带宽，并且在间断点处波形起伏较大，波形失真严重；图3(f)中，波形的过渡带明显变窄，且间断点处波形的起伏减小；图3(g)中单窗情况下的横截面波形图与无窗情况下性能表现差不多；图3(h)为双窗全相位重建的横截面波形图，可以清楚地看到间断点处波形基本平滑， Gibbs 伪影已基本消除。

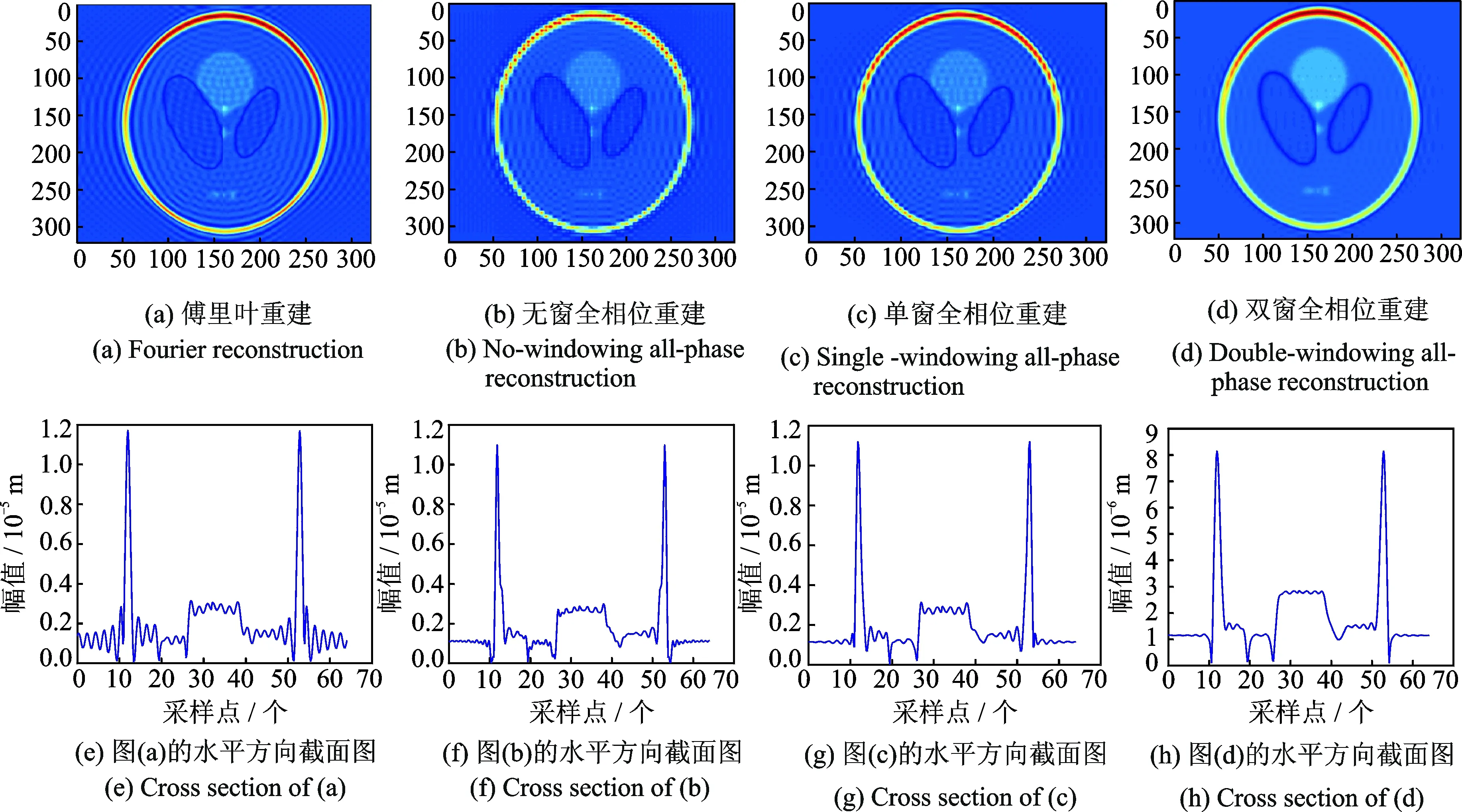
图3 MRI图像实验结果Fig.3 Reconstructed MRI images

为了进一步对实验结果进行说明，引入了量化的评价指标：归一化均方误差(Normalized mean squared error，NMSE)和峰值信噪比(Peak signal to noise ratio，PSNR)[10],其定义的表达式分别为

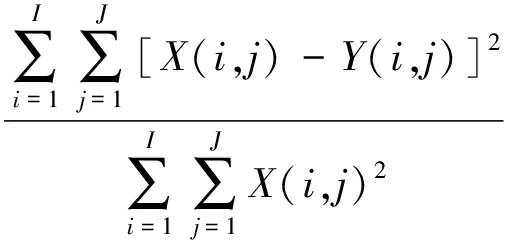
(21)

(22)

表1不同重建方法的实验结果对比

Tab．1Experimentalresultscomparisonofdifferentreconstructionmethods

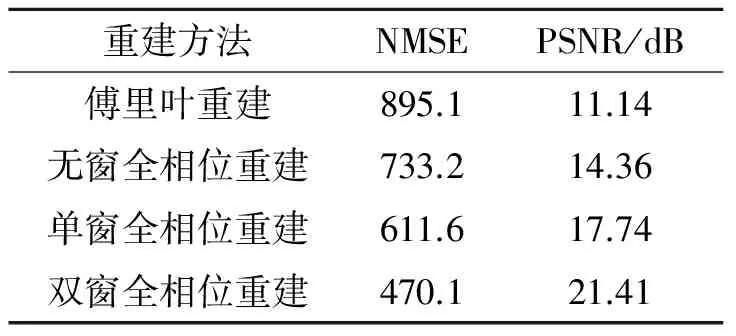
重建方法NMSEPSNR/dB傅里叶重建895．111．14无窗全相位重建733．214．36单窗全相位重建611．617．74双窗全相位重建470．121．41

式中：X(i,j)为原始图像像素值，Y(i,j)为重建图像像素值。NMSE和PSNR都是对重建图像质量的评价，其中NMSE越小，PSNR越大，则重建图像的质量越好。表1给出了不同算法重建图像的对比结果。实验结果进一步证明，本文所提方法在减小图像的Gibbs效应，改善重构图像的质量上有着明显的优势。此外，这种简单算法的运行速度比其他方法要快得多，并且和常用的滤波重构算法具有相同的复杂度，这意味着本文所提的算法具有潜在的实际应用优势。

4 结束语

本文提出了基于全相位预处理的二维傅里叶重建法，给出了运用该方法重建二维间断信号的算法流程与公式，并将该算法用于重构MRI图像。实验结果表明，相比于传统的傅里叶变换法，该方法可在不增加傅里叶系数的条件下同时有效减小图像的Gibbs效应，从而改善重构图像的质量；相比于其他非傅里叶基的重构算法，该方法仍可以使用快速傅氏变换(Fast Fourier transformation,FFT)快速算法，具有重建速度快，计算量小的特点。应当指出，全相位思想的优势在于对信号的不连续处的重构误差更小，而对于完全连续的信号，基于全相位思想的重构算法并没有绝对优势，但是由于信号处理过程中信号截断具有普遍性，而且傅氏重构法在图像重构领域有很广泛的应用，所以该方法具有很高的实用价值。

[1] Gottlieb D,Shu C W. On the Gibbs phenomenon and its resolution[J]. SIAM Review, 1997, 39(4): 644-668.

[2] 尹宝才，郭晓明，施云惠，等．一种基于分析稀疏表示的图像重建算法[J]．数据采集与处理，2014，29(1)：30-35.

Yin Baocai, Guo Xiaoming, Shi Yunhui, et al. Image reconstruction algorithm based on analysis sparse representation[J]. Journal of Data Acquisition and Processing,2014,29(1): 30-35.

[3] Jiang Mingyan, Zhu Daming, Lei Peng. The new method of reducing the NMR image′s ringing artifacts by wavelet transform[C]∥International Conference on Signal Processing. Beijing, China:IEEE, 2000,2:930-933.

[4] Adcock B, Hansen A C. Stable reconstructions in Hilbert spaces and the resolution of the Gibbs phenomenon[J]. Applied & Computational Harmonic Analysis, 2012, 32(3):357-388.

[5] Morita T, Sato K I. Mollification based on wavelets[J]. Axioms, 2013, 2(2):67-84.

[6] 吕晓琪,石静,任晓颖,等.一种基于水平集的三维肝脏磁共振图像混合分割方法[J] .数据采集与处理,2015,30(2):350-358.

Lü Xiaoqi, Shi Jing, Ren Xiaoying, et al. Hybrid segmenttation for 3D liver magnetic resonance imaging based on level set method[J].Journal of Data Acquisition & Processing,2015,30(2): 350-358.

[7] 黄翔东. 全相位数字信号处理[D]. 天津:天津大学, 2007.

Huang Xiangdong. All-phase digital signal processing[D]. Tianjin:Tianjin University, 2007.

[8] 黄翔东,王兆华,李文元. 用全相位傅氏法重构间断信号[J]. 通信学报, 2005, 26(9): 93-96.

Huang Xiangdong, Wang Zhaohua, Li Wenyuan. Using all-phase Fourier method to reconstruct discontinuous signal[J]. Journal on Communications, 2005,26(9):93-96.

[9] Sheng Yuxia, Chai Li, Zhang Jingxin. Robust optimal post-filter in oversampled lapped transform: Theory and application in image coding[J]. IEEE Transactions on Signal Processing, 2013,93(9):2516-2524.

[10] Wang Y, Yang J, Yin W, et al. A new alternating minimization algorithm for total variation image reconstruction[J]. SIAM Journal on Imaging Sciences, 2008, 1(3): 248-272.

ReductionofGibbsRingingArtifactBasedonAll-PhasePre-processing

Chu Jinghui, Wang Xiaona, Huang Xiangdong, Lü Wei

(School of Electronic Information Engineering, Tianjin University, Tianjin, 300072,China)

As an important tool of signal processing, classical Fourier reconstruction does well in reconstructing continuous signals, but it also suffers from Gibbs artifact for reconstruction of discontinuous signals. Since Gibbs artifact causes serious edge distortion and greatly degrades the quality of image, this paper presents an improved 2D all-phase Fourier reconstruction algorithm. The algorithm incorporates multiple higher-frequency harmonics with a limited number of discrete Fourier transform (DFT) coefficients, and therefore it can reconstruct discontinuous signals with higher precision. When the proposed algorithm is applied to magnetic resonance imaging (MRI) image reconstruction, experimental results show that, compared with the classical Fourier transform, the proposed algorithm can restrain Gibbs artifact more effectively and improve the quality of reconstructed images under the condition of the same amount of 2D Fourier coefficients.

classical Fourier reconstruction; magnetic resonance imaging; Gibbs artifact; all-phase

国家自然科学基金(61271609)资助项目。

2015-06-12；

2015-11-06

TN911.7