强化狼群等级制度的灰狼优化算法

2017-12-15张新明程金凤

数据采集与处理 2017年5期

关键词：等级制度灰狼狼群

张新明涂强康强程金凤

(1.河南师范大学计算机与信息工程学院，新乡, 453007;2.河南省高校计算智能与数据挖掘工程技术研究中心，新乡, 453007)

强化狼群等级制度的灰狼优化算法

张新明1,2涂强1康强1程金凤1

(1.河南师范大学计算机与信息工程学院，新乡, 453007;2.河南省高校计算智能与数据挖掘工程技术研究中心，新乡, 453007)

针对灰狼优化(Grey wolf optimization, GWO)算法在处理复杂优化问题时优化精度不高，易陷于局部最优等问题，提出了一种强化狼群等级制度的灰狼优化(GWO based on strengthening the hierarchy of wolves, GWOSH)算法。该算法为灰狼个体设置了跟随狩猎和自主探索两种狩猎模式，并根据自身等级情况来控制选择狼群的狩猎模式。在跟随狩猎模式中，灰狼个体以等级高于自身的灰狼的位置信息来指引自己到达最优解区域；而在自主探索模式中，灰狼个体会同时审视等级高于自身的灰狼的位置信息和自身位置信息，并基于这些信息自主判断猎物的位置，同时两种更新模式都将引入优胜劣汰选择规则来确保种群的狩猎方向。对12个基准测试函数进行优化的结果表明：与已有的算法相比，GWOSH算法的全局搜索能力更强，更能有效避免易早熟收敛的问题，更适用于求解高维的复杂优化问题。

智能优化算法；灰狼优化算法；社会等级制度；狩猎模式；复杂优化问题

引言

群体智能优化算法源于对自然界中生物进化过程或觅食行为的模拟[1]，其中具有代表性的有蚁群优化算法[2]，粒子群优化算法[3]，细菌觅食算法[4]和人工蜂群(Artificial bee colony, ABC)算法[5]等。这些算法都具有良好的自组织学习性和高效的搜索机制，在复杂优化问题的求解上有着突出的表现，目前已成为优化领域的研究热点。同时这些算法也各具特色，如蚁群算法采用了正反馈机制完成种群间的信息传递，并通过蚂蚁个体的共同协作以实现最终收敛于最优路径的目的,但算法局部搜索能力差，收敛速度慢且优化性能受参数设置影响较大;粒子群优化算法机制简单，具有较高的运行效率，且受问题维数影响较小，但算法易陷入局部最优，搜索性能也过于依赖参数设置;细菌觅食优化算法具有较好的局部搜索能力，但算法结构复杂，运行效率偏低;ABC算法鲁棒性强，适用于各种复杂连续优化问题，且不敏感于参数和初值的选择，但算法搜索精度不高且随机性过强。依据无免费午餐定理，没有一种算法完全适用于所有问题的求解，研究者们便通过不断提出新的算法和对已有算法性能的改进来达到寻求更好解决方案的目的。

灰狼优化算法(Grey wolf optimization, GWO)是Mirjalili于2014年提出的一种新颖的群体智能优化算法[6]。该算法模拟了自然界中灰狼家族的社会等级制度和群体狩猎行为，算法中等级最低的ω狼在等级较高的α狼，β狼和δ狼的带领下，通过跟踪猎物、包围猎物和攻击猎物来完成狩猎，属于一种有导向的随机性启发式算法。GWO算法因具有不过分依赖参数设置、全局搜索能力强和易于实现等优点，目前已成功应用于作业车间调度[7]、工程优化[8]、支持向量机分类[9]和经济调度指派[10]等领域，有效地解决了多种优化问题。但GWO在解决复杂优化问题时仍然容易过早陷入局部极值，即出现早熟收敛的现象[11]。

为了克服上述不足，基于灰狼家族的社会等级制度对于狼群狩猎影响的深入分析，提出了一种强化狼群等级制度的灰狼优化(GWO based on strengthening the hierarchy of wolves, GWOSH)算法。该算法为灰狼个体设置了两种狩猎模式：跟随狩猎模式和自主探索模式，并根据决策因子来选择狼群的狩猎模式。对12个基准测试函数的仿真结果表明，与原始的GWO[6]、双模飞行的粒子群优化(Particle swarm optimization with double-flight modes，DMPSO)算法[12]、正弦差分进化算法(Sinusoidal differential evolution, SinDE)[13]和ABC[5]算法相比，GWOSH能较好地寻得全局最优解，且比原始的GWO算法具有更快的收敛速度。

1 原始灰狼优化算法

灰狼优化算法是一种基于种群的元启发式优化算法，它模拟了自然界中灰狼家族的社会等级制度和其群体的狩猎行为。

1.1 灰狼家族的社会等级制度

图1 灰狼种群等级制度示意图Fig.1 Sketch map of the hierarchy of grey wolf

自然界中的灰狼是一种以群居生活为主的食肉动物，它们之间有着严格的等级管理制度，图1给出了灰狼种群等级制度的示意图。灰狼家族中的狼按照社会地位从高到低可以划分为4类，分别是：α狼、β狼、δ狼和ω狼。如图1所示，α狼是处于社会顶层的狼，也叫“头狼”，它是狼群的最高统治者和管理者，负责决定狼群狩猎的时间、地点及战术。位于第2层的是β狼，相当于狼群中的副首领，负责接替头狼继续领带狼群。位于最底层的是ω狼，ω狼总是要必须服从其他所有地位高的狼。而属于第3层的是δ狼，δ狼必须服从α狼和β狼，但可以统治ω狼，主要负责侦查、放哨以及看护工作[14]。

1.2 GWO算法描述

在GWO算法中，首先构建灰狼的社会等级制度模型。将种群中适应度值最优的，次优的和第三优的解分别对应α狼，β狼和δ狼，而剩余的被称为ω狼。由α狼，β狼和δ狼来负责引导，ω狼则跟随着α狼，β狼和δ狼通过搜寻猎物、包围猎物和攻击猎物来完成狩猎(优化)。

(1) 包围猎物。灰狼包围猎物的数学模型为[6]

(1)

(2)

式(1)定义了灰狼与猎物之间的距离，而式(2)则定义了灰狼的最终位置。其中，t表示当前的迭代次数，XP表示猎物的位置，X表示灰狼的位置，A和C为参数向量，其计算公式为[6]

A=2a·r1-a

(3)

C=2·r2

(4)

式中:a为整个迭代过程中一个从2到0的线性递减参数，r1和r2为[0,1]之间的随机向量。

(2) 狩猎。为了模拟狼群的集体狩猎行为，总假设α狼，β狼和δ狼对于猎物的潜在位置有更好的了解。因此，在每次迭代过程中，保存当前获得的适应度值最优(α狼)、次优(β狼)及第三优(δ狼)的3头狼的位置信息，然后狼群根据这3个最优解的位置信息综合判断出个体向猎物移动的方向并更新自己的位置，其更新公式为[6]

(5)

(6)

(7)

(8)

(9)

(10)

Xt+1=(X1+X2+X3)/3

(11)

(3) 攻击猎物(开发)。为了构建灰狼攻击猎物的数学模型，根据式(3)，A为区间[-2a,2a]上的随机向量，其中a在迭代过程中是从2到0的一个线性递减参数，当|A|的值在[-1,1]内时，灰狼的下一个位置将会在它现在位置和猎物位置之间的任意位置，表示向猎物发起进攻。

(4) 搜寻猎物(探索)。灰狼主要根据α狼、β狼和δ狼的位置信息来搜寻猎物，狼群先分散开来寻找猎物然后聚集在一起来攻击猎物。为了构建分散模型，利用一个随机值大于1或小于-1的A来迫使灰狼背离猎物去探索更有希望的搜索空间，以便实现算法的全局搜索。GWO算法中的另外一个探索向量是C，从式(4)中可以看出C是[0,2]上的随机值，它能随机增加(|C|>1)或减轻(|C|<1)灰狼靠近猎物时的难易程度，使GWO算法在整个优化过程中显示出更多的随机行为，以便提高算法的全局探索能力。

2 强化狼群等级制度的灰狼优化算法

2.1 GWOSH算法的基本思想

从GWO算法可知，它的狩猎模型是先由α狼，β狼和δ狼共同负责对猎物的位置进行评估定位，然后其余个体以此为标准计算自身与猎物之间的距离，并完成对猎物的全方位靠近、包围和攻击等行为，最终完成狩猎。在这个过程中α狼，β狼、δ狼及ω狼的等级特性体现的并不是很明显，而α狼，β狼和δ狼的位置信息对于其他个体的位置更新又起着绝对的引导作用，容易致使整个狼群过早聚集于群体当前最优位置的某一邻域内。另外，探索能力还受制于两个探索参数A和C的较小取值范围，从而导致算法易陷于局部最优。

而由第1节可知，灰狼家族有着严格的社会等级管理制度，不同等级的灰狼享有不同的权利和社会分工，灰狼所属的等级越高，对猎物的情况就有更好的了解，自主能动性也越强，且这种等级制度在狼群实现团体高效捕杀猎物的过程中发挥着至关重要的作用。因此，本文提出一种强化狼群等级制度的灰狼优化算法，以期提高其性能。

2.2 GWOSH算法

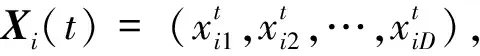
为了强化等级制度对于狼群狩猎的影响，为每个灰狼个体设计两种狩猎模式：跟随狩猎模式和自主探索模式。为了设计算法模型，作出如下假设：(1) 每头狼采用跟随狩猎模式和自主探索模式；(2) 每头狼依据一定的规则来确定其狩猎模式。跟随狩猎模式中的灰狼个体的位置更新原理类似于原始GWO算法，只是仅以等级高于自身的灰狼的位置信息来指引自己到达最优解区域；而在自主探索模式中，灰狼个体会同时审视等级高于自身灰狼的位置信息和自身位置信息，并以这些信息为基础采用随机变向的方式来更新自己的位置，同时两种更新模式都将引入优胜劣汰选择规则来确保种群的狩猎方向。

每只灰狼会根据自身所属等级情况来确定其狩猎模式。GWOSH算法先将候选解按适应度值的优劣划分为4个等级，适应度值最优者为α狼，其等级为1；适应度值次优者为β狼，其等级为2；适应度值第三优者为δ狼，其等级为3；余下的候选解为ω狼，其等级为4，记第i头狼t时刻的等级为Si(t)，则Si(t)=1表示第i头灰狼t时刻在群体中所属等级为1，Si(t)=2表示第i头灰狼t时刻在群体中所属等级为2，依次类推。然后，用决策因子DFi(t)来标记每一头灰狼个体的等级情况，其计算公式为

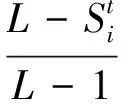
(12)

式中：L为狼群所分等级总数，即L=4。从式(12)可看出，对于等级为1的α狼而言，其决策因子DFi(t)=1，等级为2的β狼的决策因子DFi(t)=0.67，等级为3的δ狼的决策因子DFi(t)=0.33，等级为4的ω狼的决策因子为0。

在每一次的迭代过程中，对于每一个候选解都会先生成一个[0,1]间的随机数r0，如果r0≤DFi(t)，则灰狼i在t时刻就会采用自主探索模式，否则采用跟随狩猎模式。显然对于α狼因其决策因子为1，而r0恒小于或等于1，所以α狼有且仅有一种狩猎模式即自主探索狩猎模式，对于ω狼因其决策因子为0，而r0大于或等于0，所以ω狼仅能采用跟随狩猎模式。

对于α狼，其位置更新公式为

(13)

式中：k为{1,2,…,D}中的一个随机数；m和n为区间[1,N]内与i不等的随机整数，且两两互不相等；a为整个迭代过程中从2到0的一个线性递减参数，r3为区间[0,1]中的一个随机数，Xα表示具有最优适应值的α狼的位置。

对于β狼，按式(14)进行位置更新，即有

(14)

式中：k为{1,2,…,D}中的一个随机数；X1来自于式(8)；Xα和Xβ分别表示α狼和β狼的位置。

对于δ狼，其按式(15)进行位置更新，即有

(15)

式中：k为{1,2,…,D}中的一个随机数；X1和X2分别来自于式(8)和式(9)；Xα，Xβ和Xδ分别表示α狼、β狼和δ狼的位置。

对于ω狼，按式(16)进行位置更新，即有

(16)

式中：X1，X2和X3分别来自于式(8-10)。

为了确保种群的进化方向，GWOSH算法还引入了优胜劣汰选择规则来保留每一代的最优解，即如果新个体的适应度值f(new)优于上一代该个体的适应度值f(old)，则用新个体的位置替代上一代个体的位置，否则保留上一代个体的位置，该规则可表示为

(17)

GWOSH算法流程具体如下：

(1) 参数初始化。设置种群个数为N，最大迭代次数为Maxgen；

(2) 根据变量的上下界来随机初始化灰狼个体的位置Xi，其中，i=1,2,…，N；

(3) 计算狼群中每一头狼的适应度值；

(4) 按适应度值从优到差的顺序对狼群进行排序，并分别保存当前获得的具有最优、次优和第三优适应度值的灰狼的位置信息Xα，Xβ和Xδ。同时，用Si(t)来标记每个灰狼个体的所属等级，适应度值最优者Si(t)=1；次优者Si(t)=2；第三优者Si(t)=3，剩下的灰狼个体Si(t)=4；

(5) 对狼群位置进行更新。Si(t)=1，2，3和4的灰狼分别根据式(13-16)进行位置更新；

(6) 计算狼群中每一头狼的适应度值；

(7) 依据优胜劣汰选择规则，按式(17)确定是否接受该新位置；

(8) 更新参数a，A和C；

(9) 判断是否到达最大迭代次数Maxgen，若满足则停止并返回Xa的值作为最终得到的最优解，否则转到(4)。

3 仿真实验及结果分析

3.1 GWOSH算法

为了验证本文提出的GWOSH算法的性能，将其用于高维复杂函数优化计算，同时将计算结果与原始GWO、DMPSO、SinDE及ABC算法进行对比分析，其中的DMPSO和SinDE都是对其标准算法的一个有效改进，而ABC算法也是近年来提出较为新颖的优化算法，据相关文献报道其性能优于GA、PSO等传统优化算法。选取12个常用的典型高维函数进行算法性能测试分析，其表达式和全局最优解等情况如表 1所示，其中12个函数的维数都为60；f1～f4为高维单峰函数，主要用来考察算法的寻优精度；f5～f8为复杂的非线性多峰函数，由于局部极值点较多，算法较难寻找到全局最优解，因此主要用来检验算法规避早熟的能力和全局搜索的能力；同时，f9～f12是对基本测试函数进行了平移操作，使得函数具有更复杂的结构，主要用来检验算法对于未知空间的搜索能力[15-17]。本文所有实验均在CPU主频3.4GHz的Intel Core(TM)i7-3770和内存8 GB的PC机上进行，操作系统为Microsoft Windows 7，编程工具为MATLAB R2014a。

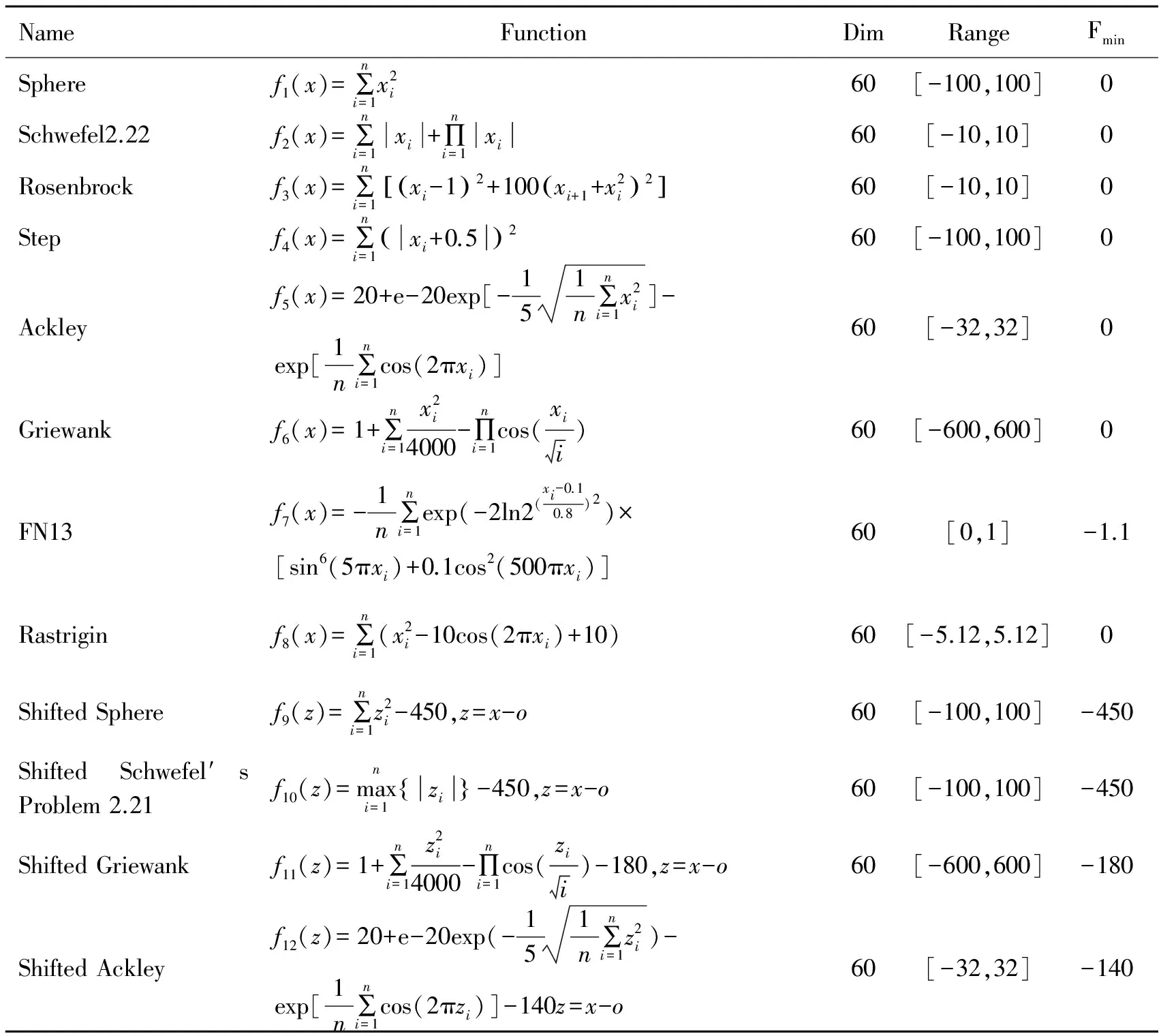
表1 测试函数

3.2 仿真实验结果

为了确保测试的公平性，在本实验中，GWOSH与原始GWO、DMPSO、SinDE以及ABC算法的种群规模和最大迭代次数设置保持一致，即每种算法种群规模统一设置为40，最大迭代次数都设置为1 000，5种算法的其他参数设置如表2所示。这些参数都设置为在保证能使各自算法的寻优效果最佳，且能够稳定收敛时所取得的值。

实验1优化性能比较。选取5个算法在12个典型函数上进行30次寻优计算的最优值(Best)、最差值(Worst)、平均值(Mean)和均方差(Std)作为各算法寻优性能的评价指标。

表2 优化算法的参数设置

Tab.2 Parameter setting of the optimization algorithms

优化算法参数设置DMPSO学习因子C1和C2均为2，惯性权重w=0．628SinDE缩放因子F=0．25ABC控制参数Limit=2400GWO参数a初始值为2GWOSH参数a初始值为2

表3-5分别列出了5个算法在12个典型函数上进行30次寻优计算的所得结果，最优者用黑体表示，图2显示了5种算法在12个典型函数上寻优过程中平均最优适应度值随迭代次数的变化情况，其中图2(a-f)，图2(h)的纵坐标均取以10为底的对数值。

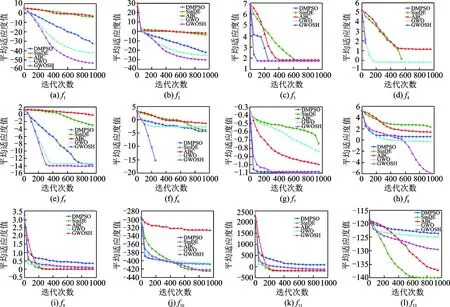
图2 5种算法在f1～f12上的收敛曲线Fig.2 Convergence curves of five algorithms on f1—f12

表3列出了5种算法对于4个单峰函数的寻优结果，由表3可知，对于f1～f4函数，GWOSH相对于其他4种算法，在搜索的最优值、最差值、平均值和均方差上均取得了最好的优化结果，尤其是在f4函数上获得了全局最优解，虽然DMPSO也在f4函数上获得了全局最优解，但根据图2中f4函数的收敛图可以看出GWOSH具有更快的收敛速度。结合表3和图2可以看出，GWOSH的收敛速度和搜索精度大幅优于其他4种算法。这是因为高等级灰狼对于猎物的位置有更好的了解，使得GWOSH中的灰狼个体仅跟随更高等级的灰狼进行寻优，避免了由于自身位置受低等级灰狼的影响所造成的解的退化，同时优胜劣汰选择规则的引入也确保了狼群的进化方向，大幅提高了搜索效率及寻优精度。

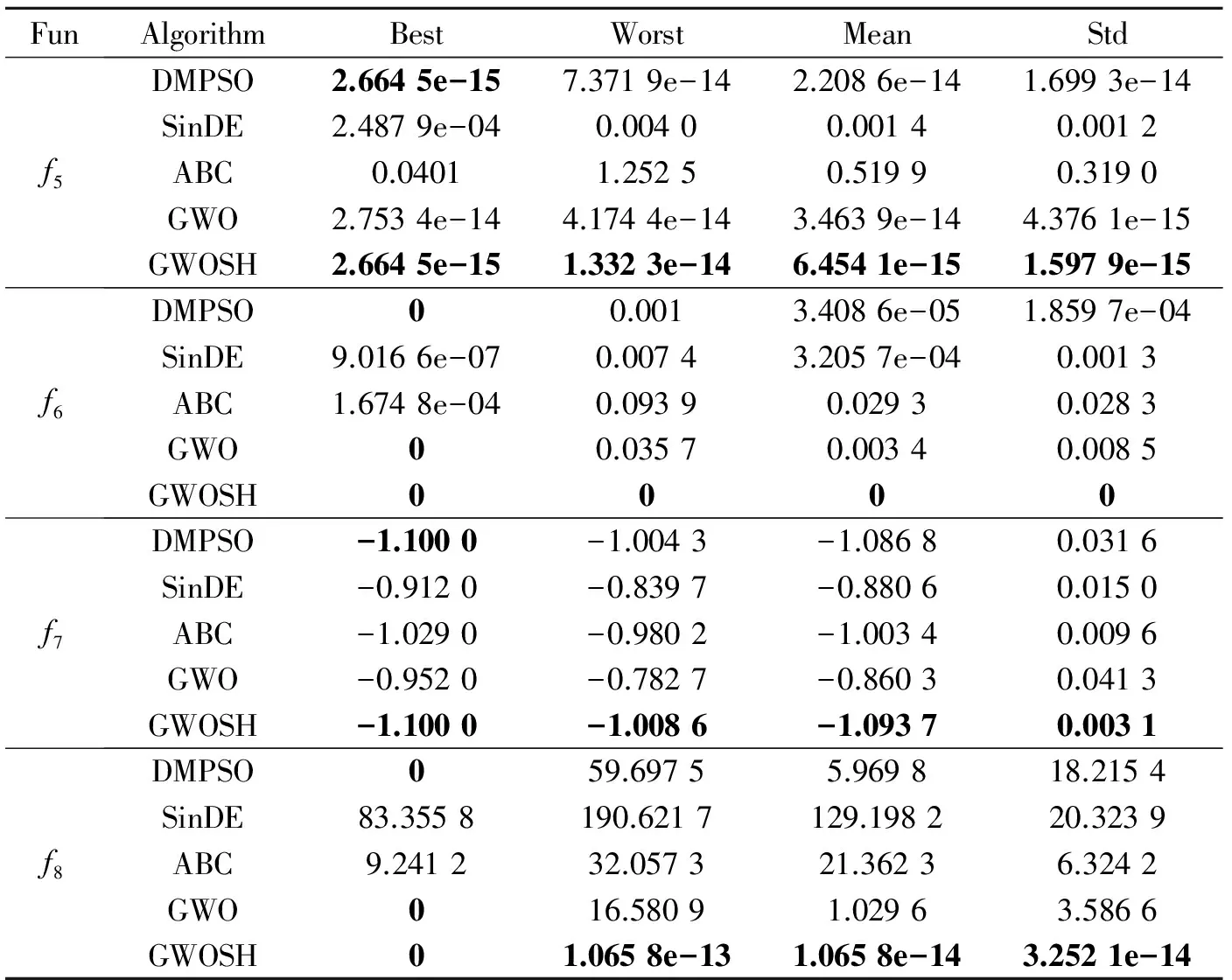
表4列出了5种算法对于4个复杂多峰函数的寻优结果，由表4可以看出，对于f5～f8函数，GWOSH在5种算法中，均获得了最好的解，尤其对于f6函数获得了全局最优解。由图2也可以看出GWOSH算法对于f5，f6，f7和f8函数具有更快的全局收敛速度，表明狼群在经过若干次迭代运算后仍具备从局部最优中跳出的能力，即使是在多模态空间，由于自由探索模式中的灰狼是以更高等级灰狼及自身所处的位置信息为参照并通过随机变向的方式来更新自身位置，增加了狼群多样性，迫使狼群不断探索新区域，从而提高了算法规避陷入局部最优的能力。

表5列出了5种算法对于4个平移函数的寻优结果，因为平移后的基准测试函数有着更加复杂的搜索空间，对于所有优化算法都是一个很大的挑战，结合表5和图2可以看出，SinDE算法对于f9，f11和f12函数有着最好的寻优效果，其次是ABC算法。虽然GWOSH在f9，f11和f12函数上的寻优效果差于SinDE和ABC算法，但其在f12函数上取得了最好的解，其最优值、最差值、平均值和均方差都优于其他4种对比算法，且GWOSH算法在4个函数上得到的最优值、最差值、平均值和均方差均要明显优于原始GWO算法，这表明GWOSH算法较原始GWO对于未知的搜索空间有着更好的寻优能力。

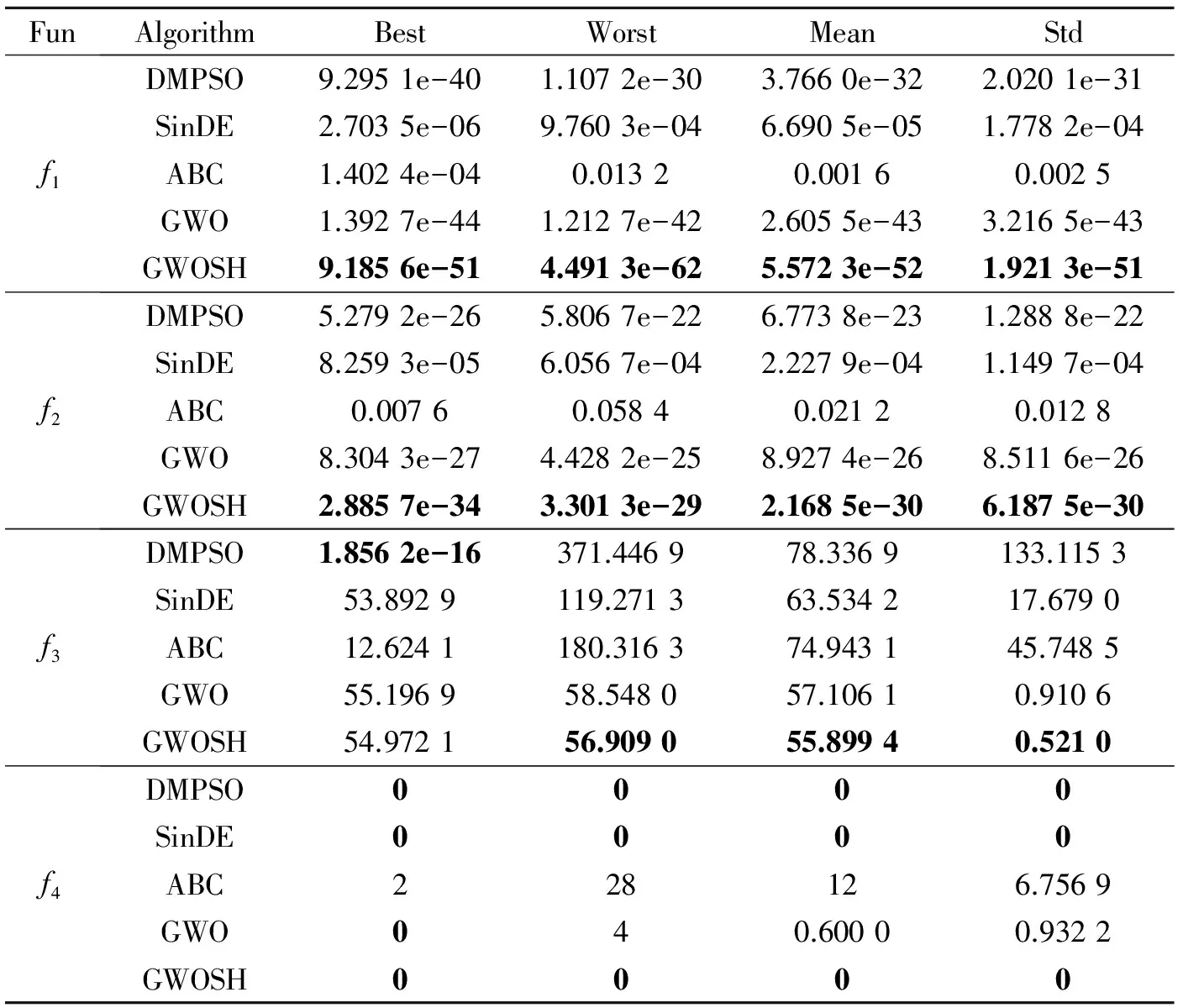
表4 5种算法在多峰函数上的测试结果对比

Tab.4 Test result comparison of five algorithms on multimodal benchmark functions

FunAlgorithmBestWorstMeanStdf5DMPSO2．6645e-157．3719e-142．2086e-141．6993e-14SinDE2．4879e-040．00400．00140．0012ABC0．04011．25250．51990．3190GWO2．7534e-144．1744e-143．4639e-144．3761e-15GWOSH2．6645e-151．3323e-146．4541e-151．5979e-15f6DMPSO00．0013．4086e-051．8597e-04SinDE9．0166e-070．00743．2057e-040．0013ABC1．6748e-040．09390．02930．0283GWO00．03570．00340．0085GWOSH0000f7DMPSO-1．1000-1．0043-1．08680．0316SinDE-0．9120-0．8397-0．88060．0150ABC-1．0290-0．9802-1．00340．0096GWO-0．9520-0．7827-0．86030．0413GWOSH-1．1000-1．0086-1．09370．0031f8DMPSO059．69755．969818．2154SinDE83．3558190．6217129．198220．3239ABC9．241232．057321．36236．3242GWO016．58091．02963．5866GWOSH01．0658e-131．0658e-143．2521e-14

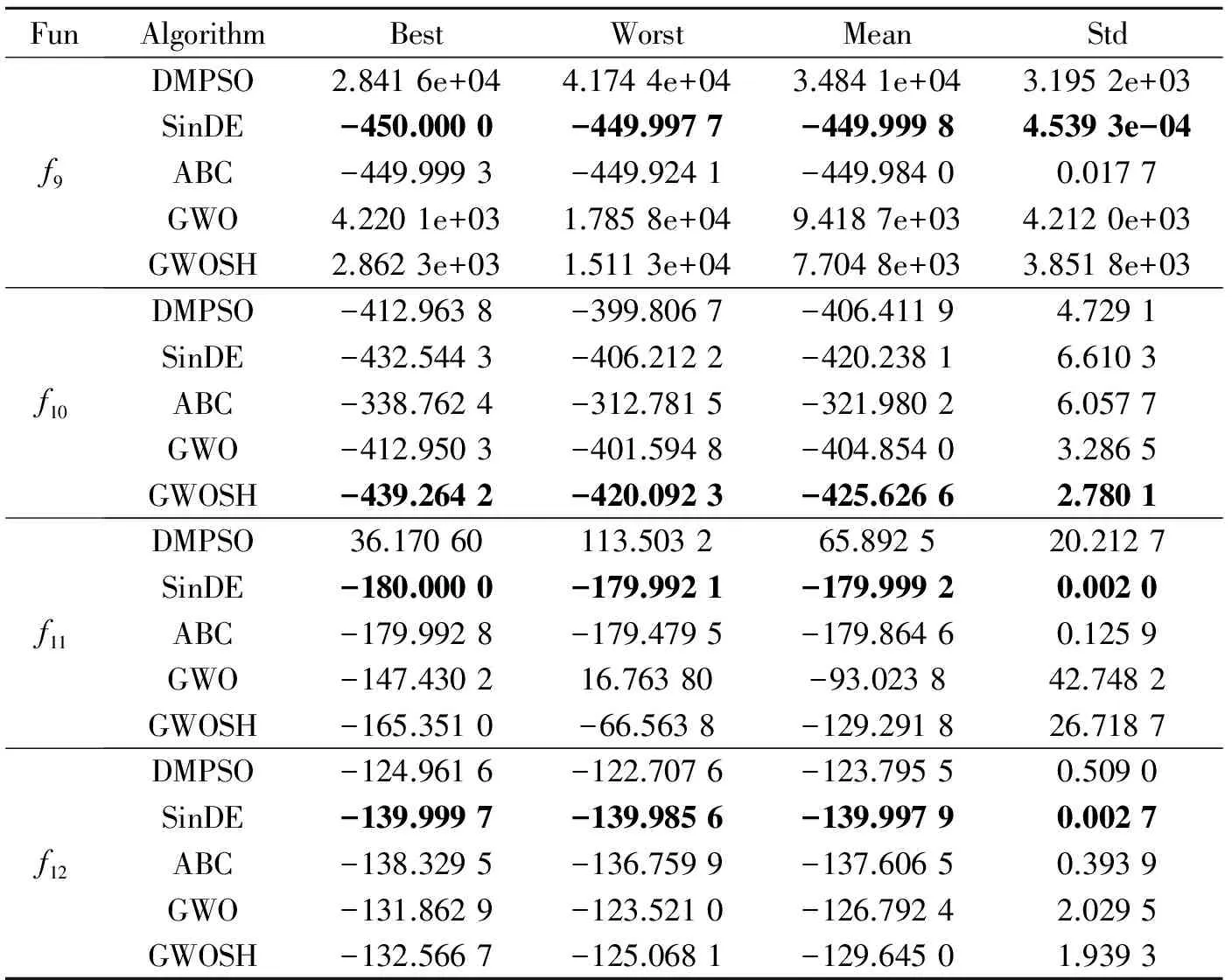
表5 5种算法在平移函数上的测试结果对比

实验2运行时间比较。表6列出了5种算法对于12个优化函数独立运行30次的平均运行时间，其单位为s。因为本文实验采用最大迭代次数作为算法终止条件，且每种算法种群规模相同，即最大函数评价次数相同，函数计算耗时相同，故表6的时间差异可反映各算法自身结构的差异。由表6可以看出，相对于其他4种算法，GWOSH的运行时间最少，表明其具有较快的寻优速度。因为该算法虽然有两种搜索模式，但二者交替进行，无需额外的计算，而且在算法设计模式上，DMPSO，SinDE和ABC在计算适应度函数值时均采用串行计算的方式，而GWOSH的设计可采用大规模的并行运算模式，从而大幅提高了算法的运行速度。而GWO算法直接采用该算法原创者提供的代码，未对代码进行优化处理和采用串行计算模式，故其耗时比GWOSH多。综上所述，GWOSH算法不管在单模态函数、多模态函数，还是平移的复杂函数上，与原始GWO算法相比都具有更优秀的优化性能，单模态函数和多模态函数的优化性能超过DMPSO、SinDE和ABC算法，所以本文算法的改进是有效和可行的。

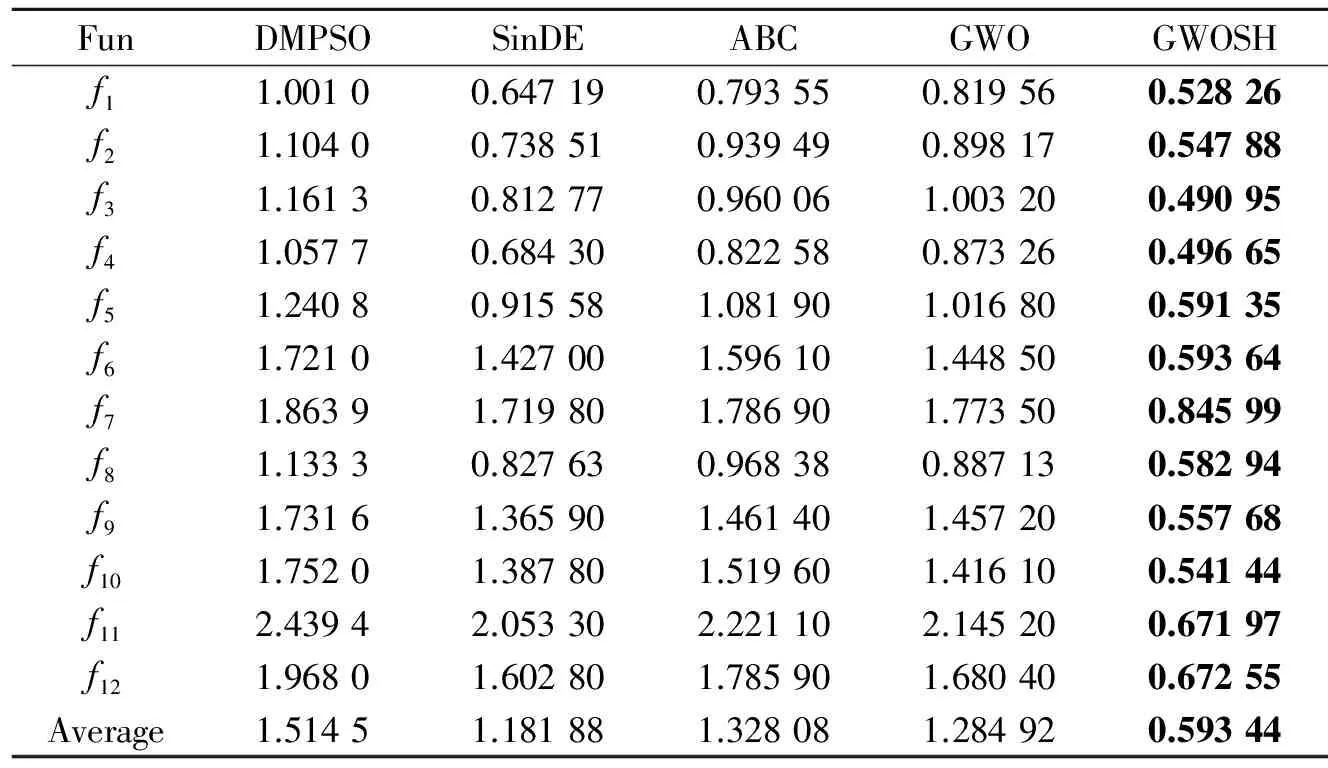
表6 5种算法运行时间的对比

4 结束语

GWO算法是最近提出的群智能优化算法，有许多方面值得研究。本文针对原始GWO算法在优化过程中存在的易陷入局部最优等缺点，基于自然界中灰狼的等级制度对于狼群狩猎影响的深入分析，提出了一种强化狼群等级制度的灰狼优化算法。该算法中的灰狼个体具有跟随狩猎模式和自主探索模式两种狩猎模式，可根据决策因子来控制选择狼群的狩猎模式。这两种狩猎模式既能充分体现狼群中高等级灰狼对低等级灰狼的引领作用，又能在充分挖掘种群位置信息的基础上发挥个体的自主能动性，提高种群的多样性，避免陷入局部最优。仿真实验结果表明：本文提出的改进策略是有效的，改进算法的全局搜索能力更强，更适用于求解高维的复杂优化问题。

[1] Sundar S, Singh A. A swarm intelligence approach to the quadratic minimum spanning tree problem [J]. Information Science, 2010, 180(17): 3182-3191.

[2] Zhang X M, Song W, Feng W. Improved ant colony algorithm for parameter estimation on the BISQ mode [J]. Inverse Problems in Science and Engineering, 2015, 23(6): 997-1010.

[3] 王养廷, 闫文忠. 分组信息共享的量子粒子群优化算法的改进 [J]. 数据采集与处理, 2013，28(3): 363-370.

Wang Yangting, Yan Wenzhong. Improvement of grouped information sharing particle swarm optimization based on quantum [J]. Journal of Data Acquisition and Processing, 2013, 28(3): 363-370.

[4] 张新明, 尹欣欣, 冯梦清. 动态高斯变异和随机变异融合的自适应细菌觅食优化算法 [J]. 计算机科学, 2015, 42(6): 101-106.

Zhang Xinming, Yin Xinxin, Feng Mengqing. Adaptive bacterial foraging optimization algorithm based on dynamic Gaussian mutation and random one for high dimensional function [J]. Computer Science, 2015, 42(6): 101-106.

[5] 张新明, 魏峰, 牛丽平, 等. 混合排名映射概率和混沌搜索的ABC算法 [J]. 计算机科学, 2014, 41(2): 102-106.

Zhang Xinming, Wei Feng, Niu Liping, et al. Artificial bee colony algorithm based on hybrid rank mapping probability and chaotic search [J]. Computer Science, 2014, 41(2): 102-106.

[6] Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer [J]. Advances in Engineering Software, 2014, 69(3): 46-61.

[7] KoMaki G M, Kayvanfar V. Grey wolf optimizer algorithm for the two-stage assembly flow shop scheduling problem with release time [J]. Journal of Computational Science, 2015, 8: 109-120.

[8] Sulaiman M H, Mustaffa Z, Mohamed M R, et al. Using the gray wolf optimizer for solving optimal reactive power dispatch problem [J]. Applied Soft Computing, 2015, 32(C): 286-292.

[9] Mirjalili S. How effective is the grey wolf optimizer in training multi-layer perceptrons [J]. Applied Intelligence, 2015, 43(1): 150-161.

[10] Song H M, Sulaiman M H, Mohamed M R. An application of grey wolf optimizer for solving combined economic emission dispatch problems [J]. International Review on Modelling and Simulations, 2014, 7(5):838-844.

[11] Zhu A J, Xu C P, Zhi L, et al. Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC [J]. Journal of Systems Engineering and Electronics, 2015, 26(2): 317-328.

[12] 李景洋, 王勇, 李春雷. 采用双模飞行的粒子群优化算法 [J]. 模式识别与人工智能, 2014, 27(6): 533-539.

Li Jingyang, Wang Yong, Li Chunlei. Particle swarm optimization algorithm with double-flight modes [J]. Pattern Recognition and Artificial Intelligence, 2014, 27(6): 533-539.

[13] Draa A, Bouzoubia S, Boukhalfa I. A sinusoidal differential evolution algorithm for numerical optimization [J]. Applied Soft Computing, 2015, 27(27): 99-126.

[14] Pilot M, Branicki W, Jędrzejewski W, et al. Phylogeographic history of grey wolves in Europe [J]. Bmc Evolutionary Biology, 2010, 10(1):104.

[15] Kiran M S, Findik O. A directed artificial bee colony algorithm [J]. Applied Soft Computing, 2015, 26(C):454-462.

[16] Hakli H, Uguz H. A novel swarm optimization algorithm with Levy flight [J]. Applied Soft Computing, 2014, 23(5): 333-345.

[17] Tanweer M R, Suresh S, Sundararajan N. Self regulating particle swarm optimization algorithm [J]. Information Sciences, 2015, 294: 182-202.

GreyWolfOptimizationAlgorithmBasedonStrengtheningHierarchyofWolves

Zhang Xinming1,2, Tu Qiang1, Kang Qiang1, Cheng Jinfeng1

(1.College of Computer and Information Engineering, Henan Normal University, Xinxiang, 453007, China; 2.Engineering Technology Research Center for Computing Intelligence & Data Mining, Xinxiang, 453007, China)

Aiming at the low precision and local optima stagnation of the grey wolf optimization (GWO) algorithm in dealing with complex optimization problems, a grey wolf optimization algorithm based on strengthening the hierarchy of wolves(GWOSH) is proposed. The new algorithm provides two kinds of hunting-modes which are following hunting mode and self-exploration mode for each grey wolf, and each grey wolf chooses its hunting-mode according to the social hierarchy of their own. In the following hunting mode, the grey wolf only depends on the position of higher level wolves to guide itself to search the optimal area. In the self-exploration mode, the individuals will examine the location of the higher level grey wolf and its position at the same time, and judge the position of prey independently based on these information. In the two hunting-modes, a survival of the fittest selection rule is introduced to ensure the evolutionary direction of the population. The optimization results on 12 benchmark functions show that GWOSH has stronger global searching ability and is more effective in the premature convergence avoidance and more suitable for solving high-dimensional complex optimization problems compared with the available algorithms.

intelligent optimization algorithm; grey wolf optimization algorithm; social hierarchy; hunting-modes; complex optimization problems

河南省重点科技攻关(132102110209)资助项目；河南省基础与前沿技术研究计划(142300410295)资助项目。

2016-03-31；

2016-04-19

TP181