基于人工蜂群算法与支持向量机融合技术的大坝变形监测研究

2017-12-15沈丽丽

水利技术监督 2017年5期

沈丽丽

沈丽丽

（辽阳通源水利水电工程有限公司，辽宁辽阳 111000）

传统人工蜂群算法计算流程复杂，计算时间长，为此文章引入支持向量机模型，将模型和人工蜂群算法进行融合，对人工蜂群算法进行优化并行计算，并将融合模型用于辽宁某大坝变形监测应用中。研究结果表明：融合模型可提高模型计算速率，模型计算结果更为稳定；相比于未融合的人工蜂群算法，融合模型在大坝变形监测的精度更高，融合模型均方误差降低0.45，平方相关系数提高0.62。研究成果对于大坝变形监测技术提供参考。

人工蜂群算法；支持向量机；模型融合；大坝变形监测

大坝变形有效监测对于大坝安全至关重要，为此，许多学者对大坝变形监测进行大量研究，取得一定的研究成果［1-6］，国内对于大坝变形监测的方法主要为3类，第一类为现场探测的方式，第二类为采用数值模型进行预测分析，第三类则为采用BP神经网络模型，结合监测样本数据，进行趋势的统计分析。各种大坝监测方式有优点也有缺点，现场探测的方式结合大坝实际情况出发，但是这种方式需要大量的人力和物力，且很难完成连续监测。第二种方式受到参数选择的影响较为明显，而第三种方式也是当前大坝变形监测的一种主要方式，但是传统BP神经网络模型容易出现局部最优解的情况。大坝变形监测影响因素较多，各种要素之间存在较为复杂的非线性关系，人工蜂群算法可较好的实现各非线性要素的关联，在许多变形监测方面得到具体应用［7-11］，但是传统人工蜂群算法计算流程复杂，计算时间长，存在一定的局限，而支持向量机模型可实现模型的优化计算，为此本文引入支持向量机模型，将模型和人工蜂群算法进行融合，并将融合模型用于辽宁某中型水库大坝变形监测中，研究成果对于大坝变形监测技术提供参考价值。

1 人工蜂群算法与支持向量机融合原理

人工蜂群算法通过模拟蜜蜂的群体寻优良品种的蜜源的仿生式智能计算方法，算法将蜜源即为模型的目标函数，本文为大坝变形值、引领蜂群以及跟随的蜂群个数都设置为SN，按照一定的优化方法对模型参数进行寻优求解计算，人工蜂群算法的两个主要参数为模型计算的惩罚度因子以及宽度计算参数进行优化求解，模型计算的主要有以下9个步骤。

（1）对模型算法的控制参数进行初始化设置，设定模型计算迭代的次数；

（2）通过随机方程随机产生SN个蜜源，每个蜜源对应于相应的引领蜂群，每个蜜源计算的优化可以表征为 Xi（i=1，2，…，SN），其中Xi表示为模型两个计算参数所组成的2维向量。其中Xi的计算表达式为：

式中，xij—第i个蜜蜂群所对应的第 j维的搜索的具体位置；xjmax—模型第j维上边界；xjmin—模型第j维下边界。

（3）在完成参数向量组合后，需要对模型变量进行邻域的搜索，模型采用以下公式进行邻域的变量搜索，计算公式为：

式中，K—随机数，K取值范围为（1，2，…SN）；rij∈［-1，1］之间的随机数，该数值可以控制xij的邻域的范围，邻域的范围随着xij不断搜素逐渐变小。

（4）在进行变量搜素解的构建后，需要计算每个蜂群的自适应度值，在新旧蜜源之间进行贪婪度参数的选择，若果变量搜索蜜源（目标值）高于旧的蜜源搜索值，则代替旧的蜜源搜索值进行新的蜜源计算，各个蜂群的自适应度值计算公式为：

式中，yi—模型计算的实际值，在本文为大坝变形监测点采集的监测数据；—模型预测的值，在本文为大坝变形预测数据。

（5）在完成蜂群自适应度值计算后，需要计算每个蜂群的蜜源被选择的概率P，模型所有跟随的蜂群采用轮盘机制对蜜源进行选择，当跟随蜂成为引领蜂群后，结合公式（2）进行新的蜜源的搜索，计算的公式为：

式中，fiti—模型计算的自动适应度值。

（6）在完成蜜源被选择概率P计算后，需要对模型最优求解的次进行统计：

式中，search—模型搜索次数，当 search＜limit，则模型返回到第三步骤，否则继续下一个步骤的计算。

（7）在完成优选次数计算后，需要判别是否存在需要淘汰的蜜源，如果某些蜜源经过多次循环计算后依旧不变，则需要淘汰这些蜜源，则被淘汰的蜜源对应的引领蜂正式成为侦查蜂群，新的侦查蜂群则按照方程（1）计算新的蜜源。

（8）在寻找到各个蜜源的最佳适应度后，结合参数C和g再代入模型计算。在模型计算时采用支持向量机对人工蜂群算法进行融合，对模型进行优选计算，结合支持向量机的原理确定模型支持向量机的自回归方程，计算函数为：

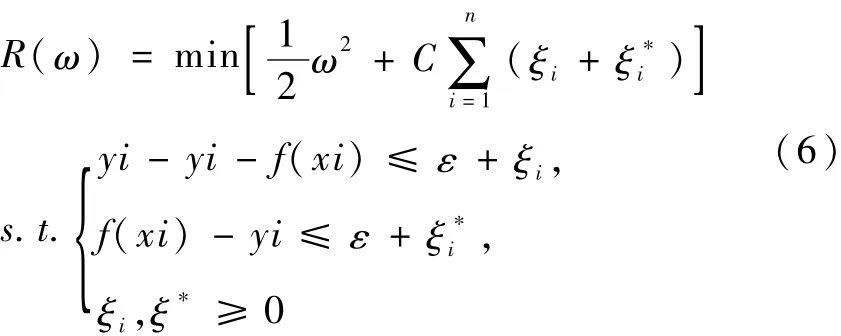
式中，C—模型惩罚系数；ξi和—模型的非线性松弛系数；ε—模型非敏感度因子。

（9）在进行自回归方程的构建后，采用拉格朗日推求方法优化求解上述方程，优化求解的方程为：

式中，K（xi-—支持向量机的核函数；ai和aj—拉格朗日系数。

经过上述变化可以得到人工蜂群与支持向量机的融合函数，融合函数的回归方程为：输入变量X即可得到需要推求的目标函数值。

2 模型在大坝变形监测的实例应用

2.1 工程实例

本次以辽宁中部某中型水库为研究工程实例，该水库全长20m，流域集水面积为42km2，该水库在构建初期，在坝体内部布设了大坝监测点，采集大坝变形监测数据，大坝变形监测点分布见图1。选取典型断面进行断面参数分析，选取的典型断面参数见表1。本次研究收集了该大坝1990～2015年的大坝变形监测数据，用于模型的样本训练计算以及模型大坝变形监测精度对比分析。

图1 大坝变形监测点分布图

表1 大坝断面主要设计参数

2.2 模型计算稳定性分析

为对比不同优化算法对人工蜂群模型计算稳定性的影响，结合支持向量机算法和传统人工蜂群算法对模型进行稳定性的测试，并结合3组样本数据组进行了分类率以及模型参数的对比分析，具体见表2和表3。其中算法1代表本文选用的支持向量机优选算法。

表2 不同算法的稳定性测试结果

表3 不同算法的计算时间测试结果

表2为支持向量机和人工蜂群算法耦合后以及传统人工蜂群算法的模型稳定性测试结果，从表2中可以看出，模型分类率表示为模型的计算效率，分类率越高，表明模型计算稳定性和计算效率越高，融合模型在三组样本数据的分类率都要高于单一算法下的分类率，表明融合计算模型的稳定性和计算效率都要好于单一算法，从三组样本数据的分类率来看，分类率均值提高7.4%。表3为不同算法的计算时间测试结果，从测试分析数据可以看出，融合模型计算的时间都要短于单一算法，计算时间相比于与单一算法，均值缩短160分钟。融合模型在三组样本数据计算时间为单一算法的1/2。可见，支持向量机和人工蜂群算法融合模型在模型稳定性和计算时间上都有较为明显的改善。

2.3 大坝变形监测对比分析

结合支持向量机和人工蜂群算法融合模型对研究水库的大坝形变进行预测，并结合大坝实测的大坝变形数据对比分析支持向量机和人工蜂群算法融合模型以及传统人工蜂群算法在大坝变形监测的预测精度，对比分析结果见表4以及图2和图3。

表4 不同模型在大坝变形监测的对比分析

图2 不同算法下的大坝变形预测值和监测值对比

图3 不同算法下的大坝变形预测值和监测值相关分析图

表4为融合模型和单一算法在研究区域大坝变形监测的预测结果，从预测值误差相对值看出，融合模型预测值和监测数据的误差相对值在-5.13%～19.2%之间，小于20%，而单一算法下预测的大坝变形值和各监测点监测值之间的误差相对值在-20.1%～38.1%之间，均在20%以上，可见融合模型在误差相对值有所改善，改善度为18.9%。其次从计算的误差绝对值可以看出，融合模型计算的误差绝对值在0.02～0.54mm，而单一算法计算误差绝对值在0.08～0.65mm，可以看出，融合模型计算的误差绝对值小于单一算法的误差绝对值，但是两个模型计算的误差绝对值差距不大，总体改善度不明显。从表中还可看出融合模型随着大坝变形监测值的增加，其误差绝对值和相对值都有所增加。为进一步分析两种模型在大坝变形监测的精度，结合20个监测点数据以及模型预测的大坝变形数据，计算了两种模型在大坝变形监测计算的均方误差以及相关平方系数，通过计算，相比于单一算法模型，融合模型的均方差误差降低0.45，平方相关系数提高0.62，融合模型相比于单一算法，在大坝变形的精度有较为明显改善。图2为不同算法下大坝变形预测值和监测值的对比，从结果上看，融合模型大坝变形监测值和监测数据的趋势和相关度都要好于单一算法的模型。综上，融合模型在大坝变形监测的精度上好于单一算法的预测精度，更适合作为大坝变形监测预测技术。