巧用类比实施自主学习——“从分数到分式”教学设计

周 莎王 瑛

巧用类比实施自主学习
——“从分数到分式”教学设计

周 莎1王 瑛2

在学习过程中，教师应关注学生的自主观察、猜想、归纳等能力，充分发挥学生学习的主动性和积极性；关注数学思想方法和探究数学问题的一般路径，提升学生的数学核心素养。依据数学学习的有效路径，在同分数的类比中引入分式的概念。

分数；分式；教学设计

本节课从学生的最近发展区出发，利用类比的数学思想，引导学生自我构建新的知识体系，复习分数的结构特征，再类比分数得到分式，本节课具体程序为：

（1）创设情境，引入新知，产生学习新知识的需要。

（2）学生自我分析，类比分数，比较异同，初步形成分式的概念。

（3）学生自主操作，深入探究，逐步形成分式的概念。

（4）学生概括形成概念，巩固概念。

基于“人在课中央”的主题，我的教学设计如下。

一、初识分式

情境引入：观看“天舟一号”发射的视频，点燃学生探索科学的激情。

提出问题：1.天舟1号货运飞船的推进舱两侧安装了一对长方形太阳能电池帆板，每个长方形的面积大约为16m2，宽约为3m，则长为__________m；

若长方形的面积为xm2，宽为3m，则长为________m；

若长方形的面积为16m2，宽为ym，则长为________m；

若长方形的面积为xm2，宽为ym，则长为________m。

2.天舟1号货运飞船的推进舱呈圆柱形，体积为 （v+a）m3，它的底面积约为6m2，则高度为_________m；若飞船推进舱的体积为（v+a）m3，底面积增加bm2，则高度为____________m。

（设计意图：围绕天舟一号顺利飞天后，展开的长方形太阳能电池帆板长度和推进舱高度，设计了6个小问题，首先让学生感受由分数到整式，再到分式，引出学习分式的必要性。类比分数，观察得出分式的结构；对比整式，得出分子、分母都是整式，且分母中含有字母。这与以往学习的分数，整式都不同，实现学生初步感知分式的目的。）

二、形成概念

代数式的排列顺序体现了从分数到分式、从整式到分式的过渡。教师向学生指出类比和归纳是探索新概念的重要方法。

学生自主思考，互动交流，通过共同研讨，继而形成分式的概念。在学生观察、归纳的基础上，教师引导学生逐步完善分式的概念：一般地，如果A、B表示两个整式，并且B中含有字母，那么式子叫作分式，其中A是分式的分子，B是分式的分母。

通过类比分数让学生剖析分式概念。

形式：与分数一样，分式也是由分子、分母和分数线组成。

内容：分数的分子分母都是整数，分式的分子分母都是整式。

要求：分式的分母中必须含有字母，分子中可以含有字母，也可以不含有字母。

（设计意图：通过学习归纳、总结，在已有知识的基础上，类比分数的基本概念，用语言叙述出分式的基本概念，培养学生的归纳总结能力、语言表达能力、抽象能力。从而达到探究新知，掌握重点的目的。）

三、巩固概念

1.请同学们举出你认为是分式的代数式，然后学生和教师共同指出是否有误。

2.小游戏：请同学们从桌子上的卡片中任意抽取两张，卡片上的整式分别作为分子和分母，使得所组成的式子为分式。根据举例情况，再判断这样的式子是否是分式，为什么？

在学生杂乱无章的排列中，教师启发学生思考有没有什么好办法能够有条理地解决好这个问题。指出问题的关键：确定分母，再确定分子，让学生能有序地解决好这个问题，并做到不重复、不遗漏。

（2）请选择一个你喜欢的a的值代入计算。

由此，巧妙地引出分式有意义、无意义及分式的值为0的条件，师生共同总结：当B≠0时，分式有意义；当B=0时，分式无意义；当A=0且B≠0时，分式

（设计意图：本例先由学生选择喜欢的值代入计算，教师深入学生中，发现问题，具体指导，最后由教师组织全班交流，水到渠成，得到分式有无意义的条件，以及分式值为0的条件，这样，教学难点得以突破，并借助于所组成的分式进行知识巩固。）

4.你能写出符合下面一个条件的分式吗？试试看。

（1）当 x=3 时分式无意义；（2）当 x=4 时分式的值为0；（3）当x=3时分式无意义且当x=4时分式的值为0。

（设计意图：通过学生的自主编题，掌握学生对分式理解的偏差，培养学生的发散思维和创新能力。）

四、深化概念

分式与整式一样都是描述数量关系的代数式，让学生从课堂融入生活，再对分式表述不同的实际意义。

让学生自己写一写，师生再共同点评。

（设计意图：鼓励学生在独立思考的基础上，积极地参与到对数学问题的讨论中，充分发表自己的观点，培养学生解决实际问题的能力。）

五、总结概念

师生共同总结课堂所学知识和所得收获。通过多媒体展示，把本节课的知识点通过知识树的形式形象地展现出来，形成知识网络，让学生感受分式与分数有许多共同之处。告知学生，学习分式，就需要与分数进行类比，在后续的学习中，还会类比分数学习分式的基本性质、运算、应用等。在学习本章之后，再让学生比较分式与分数，他们一定会体会到分式是分数概念的深化和拓展。

六、课后作业

1.下列各式哪些是整式？哪些是分式？（填序号）

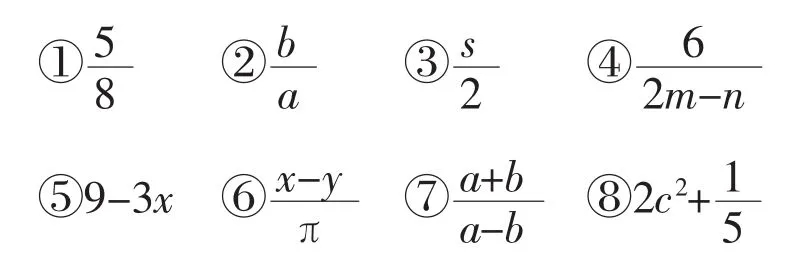
整式：____________________；

分式：_____________________

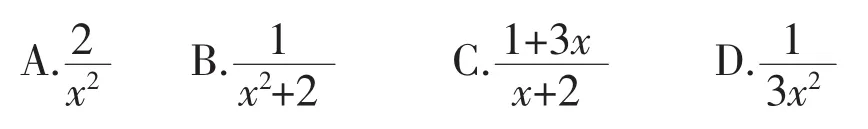
3.在分式的值是正数？

【团队推荐】

周莎老师执教的“从分数到分式”一课选自人教版数学教材八年级上册第十五章第一节。在学习本节课前，学生在小学已经学习了分数，在初一时又学习了整式的概念、运算等，学生已经初步具有“从具体到抽象，从特殊到一般”的认识事物规律的意识，为本课的学习奠定了基础。本节课是分式单元起始课，主要内容是分式的概念以及分式有意义、无意义的条件。分数和整式的知识是学习本节课的基础，类比分数引出分式的概念，进一步提升学生对“式”的认识。本节课内容也是进一步学习分式性质、运算、解分式方程以及后续学习反比例函数的基础。

本节课主要学习分式的概念及其有意义、无意义的条件。在教学中周老师选择从实际问题情境出发列代数式，在学生原有知识结构的基础上，类比分数，探究分式。在教学中让每位学生都参与到课堂中来，在自主学习的同时，加强学生的合作意识。利用多媒体课件，调动学生学习的热情。周老师这节课准备得很充分，教学思路清晰，选题典型，由浅入深，层层推进，能照顾到不同成绩段的学生。本节课采用发现式学习的方法，引导学生经历“观察、猜想，类比、发现，归纳、应用”的探究过程。

下面我来谈谈周老师这节课的教学过程。课的开始有一个情境来引入新课，一方面可以吸引学生的眼球，另一方面可以顺利引入教学内容。本节课课本教材给出面积和体积问题，列出两个分数，两个分式，进而分析类比得出分式的概念。在备课时我们觉得存在两方面问题：第一，代数式过少，说明分式的分子、分母是整式不够；第二，类比分数学习分式，分数本身也属于整式，我觉得还应类比整式与分式，从学生熟悉的知识入手更好。最终周老师决定从学生知道而且已成为热点的情境出发更好，情境问题的背景是“天舟一号”，从学生感兴趣的热点出发解决问题，从生活走进课堂。

第一阶段的初步学习完成后，接下来要形成分式的概念，让学生自主思考，互动交流，通过共同研讨，使学生生成分式的概念，进而完成第二阶段的学习。在这一阶段，自然生成的东西更容易让学生记忆深刻。

概念形成结束后，周老师并没有与以往教学一样让学生在众多代数式中寻找分式，而是把学习的过程归还到学生手中，学生是学习的主人，让他们自己列举几个分式（并指出分母中含有的字母），加深对概念的理解。接下来打破常规，通过小游戏，引导学生动手操作，通过一组卡片让学生自己组建分式，培养学生的发散思维和创新能力，培养分类意识和合作意识。这样做，自然引出了分式有无意义及值为0的条件，避免为了完成学习任务而进行题训，顺理成章地突破了本节课的难点，并且彰显了学生的主人翁意识，这是本节课的第三阶段。

概念得到巩固以后，周老师进行了拓展提高也就是本节课的第四阶段，进一步深层次地巩固概念，鼓励学生独立思考，充分发表自己的观点，培养了学生的发散思维以及解决问题的能力。这里与本节课的起始部分形成呼应，让学生体会分式与整式一样都是描述数量关系的代数式，让学生再从课堂融入生活，再对分式表述不同的实际意义，学生的踊跃发言再次活跃了课堂气氛。

最后，让学生自己总结本节课的知识点，周老师再结合学生的总结以“知识树”的形式生动、形象地展示本课内容，说明分式与分数有许多共同之处，学习分式会经常与分数进行类比，比如今后还会类比分数学习分式的基本性质、运算、应用，等等。学生学习本章之后，再比较分式与分数，一定会对分式有更深入的理解。

本节课的学习过程中周老师始终关注学生自主观察、猜想、归纳的能力，充分发挥了学生学习的主动性和积极性；关注数学思想方法和探究数学问题的一般路径，提升了学生的数学核心素养。

G633.6

A

1005-6009（2017）59-0035-03

1.周莎，江苏省泰州中学附属初级中学（江苏泰州，225300）教师，二级教师；2.王瑛，江苏省泰州中学附属初级中学（江苏泰州，225300）教师，高级教师。

（推荐人：王 瑛）