一种具有小世界性常数度的数据中心网*

李梅生 肖文俊 赖正文 张占英 韩冬

(1.华南理工大学 计算机科学与工程学院， 广东 广州 510006； 2.广东金融学院 互联网信息与金融工程系， 广东 广州 510520; 3.华南理工大学 软件学院， 广东 广州 510006)

一种具有小世界性常数度的数据中心网*

李梅生1,2肖文俊3†赖正文1张占英1韩冬2

(1.华南理工大学 计算机科学与工程学院， 广东 广州 510006；
2.广东金融学院 互联网信息与金融工程系， 广东 广州 510520; 3.华南理工大学 软件学院， 广东 广州 510006)

先义了一个常数度代数图Gcoset，在此基础上构造了8度正则度、对称性良好的数据中心网络的虚拟化拓扑结构GDCN；然后详细描述了GDCN的静态模型以及Gcoset的路由算法，并给出了GDCN结构以及一个具体实现；最后将GDCN与其他数据中心网络模型进行了对比.结果表明：GDCN的直径仅为O(logN)；Gcoset的路由算法较为简单；GDCN结构简单、通信性能较高，可扩展性良好，且具有良好的路由容错性.

常数度；数据中心网；小世界性；虚拟化；拓扑结构；路由算法

作为可用于存储、计算等服务，同时又具有成本效益的基础设施，数据中心受到了广泛的关注.如今，亚马逊、谷歌、脸谱网、雅虎等公司均已将数据中心用于数据存储、网络搜索和高性能计算等[1- 5].作为数据中心的核心，数据中心网络需要将部署在数据中心的成千上万台服务器通过交换机等网络设施连接起来，组成具有低成本、高带宽、高可用性、高可靠性和负载均衡的服务网络[6].

目前，数据中心网络(DCN)主要分为以交换机为中心的结构和以服务器为中心的结构[7].在以交换机为中心的结构中，数据转发功能完全依靠交换设备(交换机)来完成，服务器的作用仅限于计算与存储等；以服务器为中心的结构中，服务器除了要完成计算与存储功能外，还需要实现数据包的路由选择与转发功能.文献[8- 9]提出了交换机和服务器都具有数据转发和路由选择功能的双中心结构.随着虚拟技术的广泛应用，文献[10]提出了DCN虚拟化的解决方法，基于虚拟网络的数据中心网络结构被提出.在数据中心网络结构中，包括有Fat-Tree[11],DCell[12],BCube[13]和FiConn[14]等.

在Fat-Tree中，n个端口的交换机被分成n个pod，每个pod包含2层，即边缘层和聚合层，每层n/2台交换机.边缘层的交换机用一半数量的端口连接主机，剩余一半端口连接聚合层交换机.在Fat-Tree的核心层有(n/2)2台n端口的核心交换机.核心交换机的每个端口分别连接不同的pod中的聚合层交换机.因此，Fat-Tree可连接n3/4台主机.

DCell采用层次结构通过递归方式将较小的网络单元通过互连方式形成更大的网络结构.在DCell中，DCell0是最小的基本单元，由一台n(n≤8)个端口的微型交换机和连接到交换机上的n台服务器构成.n+1个DCell0通过服务器之间的互连可获得DCell1；其互连规则是：第i个DCell0中的第j-1台服务器连接到第j个DCell0中的第i台服务器上.

BCube是以服务器为中心的互连拓扑结构，是一种采用分层、递归方式构造的数据中心网结构.一个BCube0是由一台n端口交换机和连接到交换机上的n台服务器构成，BCube1是由n台n个端口交换机将n个BCube0连接而构成.更一般地，一个BCubem是由n台n端口交换机将n个BCubem-1连接而构成.因此，在BCubem中，每台服务器有m+1个端口.

FiConn也是层次模型，与DCell相似采用递归方式形成网络结构.然而，FiConn中的每台服务器仅有2个网络端口，即仅有2条链路，因而将遭受负载均衡问题.

近年来，对小世界网络现象[15]的研究也对数据中心网络产生了影响.小世界网络具有两个性质：路径长度短，聚集系数(Clustering Coefficient)较大.对于数据中心网络而言，路径长度短意味着随机选择的两个节点之间的跳数较小，聚集系数较大意味着网络有可能在高负载的条件下保持良好的性能.文献[16]指出具有小世界网络性质的数据中心网络具有较好的容错性，对突发性的高负载具有一定的优势.

文中定义了一个常数度代数图Gcoset，然后在此基础上构建了一个数据中心网络的虚拟化拓扑结构GDCN，描述了GDCN的静态模型和Gcoset的路由算法；并给出了GDCN结构以及一个具体实现；最后将GDCN与其他DCN进行了对比.

1 GDCN的静态模型

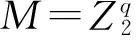
∀(x1,y1),(x2,y2)∈G,有

(x1,y1)•(x2,y2)=(σy2(x1⊕x2),y1+y2).

其中：“⊕”是异或操作，“+”是模q加法操作,σy定义为

显然，运算“•”在G上是封闭的，但是“•”不满足结合律，因此代数系统(G,•)是广群.

广群(G,•)有如下性质：

(1)有右单位元(0q,0).

(2)有右逆元，元素(x,y)的右逆元为(x,-y).

(3)既不存在左零元，也不存在右零元.

(4)不满足交换律.因此规定：(g1•g2)•g3简写为g1•g2•g3或者g1g2g3(∀g1,g2,g3∈G).

(5)满足右消去律，即

∀(x1,y1),(x2,y2),(x,y)∈G,

如果(x1,y1)•(x,y)=(x2,y2)•(x,y),

则(x1,y1)=(x2,y2).

定义2 设(x,y),(x′,y′)∈G，如果对任意的g∈G，有g•(x,y)•(x′,y′)=g，则称(x′,y′)是(x,y)在G上的单侧逆元，简称为(x′,y′)是(x,y)的单侧逆元，记为(x,y)T.

在(G,•)中，有∀(x,y)∈G，其单侧逆元(x,y)T=(σ-y(x),-y)，同时，(x,y)T的单侧逆元为(x,y).因此，有下面结论.

结论1 元素(x,y)的单侧逆元是唯一的.

为了后面讨论方便，作如下标记:设S⊆G，记ST={sT|s∈S}.

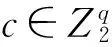
下面给出Gcoset(G,S)图的定义，首先定义一个子集S：

S=Sc∪St∪Sr∪Sd.

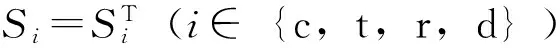
定义3Γ=Gcoset(G,S)是由G和S确定的代数图定义为

V(Γ)=G，E(Γ)={(g,gs)|g∈G,s∈S}.

对任意的边(g,gs)∈E(Γ),有g∈G,s∈S；由S=ST可知，sT∈S，于是有gssT=g，故(gs,g)∈E(Γ)，因此图Γ是无向图.图1是结点(0q,0)及其邻居的邻接情况，实线为与结点(0q,0)直接相连的边，而虚线为邻居间的连接边.

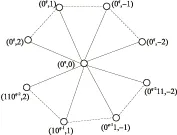
图1 结点(0q,0)及其邻居的邻接情况

图Γ有如下性质：

(1)Γ是连通的无环图;

(2)Γ是8度正则图;

(3)Γ是点传递图;

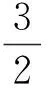
Γ的直径可以在后面的路由算法中得到验证.

对于给定的q值，图Γ的结点数为N=2q×q，因此可得性质(5).

(5)Γ的直径为O(logN)；

由于Γ图是点传递的，所有结点的聚集系数是相同的.这里考虑结点(0q,0)，由图1可知，结点(0q,0)有8个邻居，邻居间有6条边，因此，根据聚集系数的定义有性质(6).

(6)Γ的聚集系数CC=2×6/(8×7)=0.214.

定义4 称边{(g,gs)|g∈G,s∈Sc}为c边，完全由c边构成的圈称为c圈，边{(g,gs)|g∈G,s∈St}称为t边，完全由t边构成的圈称为t圈，边{(g,gs)|g∈G,s∈Sr}称为r边，完全由r边构成的圈称为r圈，边{(g,gs)|g∈G,s∈Sd}称为d边，完全由d边构成的圈称为d圈.

在图Γ中有如下结论.

结论2 在图Γ中，c圈是存在的，Gcoset(G,S)共有2q个c圈，并且每个c圈有q个顶点.

结论3 在图Γ中，当q>4时，t圈是存在的，当2|q=0时Γ中共有2q+1个t圈，并且每个t圈有q/2个顶点，否则Γ中共有2q个t圈，并且每个t圈有q个顶点.

结论4 在图Γ中，r圈是存在的，Γ中共有2q个r圈，并且每个r圈有q个顶点.

结论5 在图Γ中，d圈是存在的，Γ中共有2q个d圈，并且每个d圈有q个顶点.

2 Gcoset的路由算法

设源结点(cx,rx)=(x1,x2,…,xq,rx)、目的结点(cy,ry)=(y1,y2,…,yq,ry)，可以得到静态拓扑的简单路由算法(记为算法1)，如下文所示.

输入：源结点(x1,x2,…,xq,rx)和目的结点(y1,y2,…,yq,ry)

Step1:compute Δr=ry-rx

Step2:

if(|Δr|<⎣q/2」)

fori=1 to|Δr| do

if(Δr>0)then

go to the node(x1,x2,…,xq,rx)•(0q,1);

else

go to the node(x1,x2,…,xq,rx)•(0q,-1);

else

fori=1 toq-|Δr| do

if(Δr>0)then

go to the node(x1,x2,…,xq,rx)•(0q,-1);

else

go to the node(x1,x2,…,xq,rx)•(0q,1);

Step3:

fori=1 to q do

if(x1≠yi)then

go to the node(x1,x2,…,xq,rx)•(10q-1,-1);

else

go to the node(x1,x2,…,xq,rx)•(0q,-1);

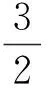
在算法1的路由选择中，如果当前结点为v，则选择下一步的节点时只考虑了节点v的部分邻居结点(即v•s，其中s∈Sc∪Sr).此外，算法1是单点源路由算法.下面给出Gcoset的分布式算法(记为算法2).

输入：当前结点(x1,x2,…,xq,rx)，目的结点(y1,y2,…,yq,ry)

输出：下一跳的标识符

if((x1,x2,…,xq)=(y1,y2,…,yq)andrx=ry)

the destination has been reached.

else{

Δr=(8+ry-rx)mod 8;

if((x1,x2,…,xq)=(y1,y2,…,yq)){

if(Δr=1)

return(x1,x2,…,xq,rx)•(0q,1);

else if(Δr<=4)

return(x1,x2,…,xq,rx)•(0q,2);

else if(Δr<7)

return(x1,x2,…,xq,rx)•(0q,-2);

else if(Δr=7)

return(x1,x2,…,xq,rx)•(0q,-1);

}

else{

∥(y1,y2,…,yq)循环左移Δr位

(z1,z2,…,zq)=(y1,y2,…,yq)<<<Δr;

if(x1=z1andx2=z2)

return(x1,x2,…,xq,rx)•(0q,-2);

else if(x1=z1)

return(x1,x2,…,xq,rx)•(0q,-1);

else if(x1≠z1andx2≠z2)

return(x1,x2,…,xq,rx)•(110q-2,-2);

else if(x1≠z1)

return(x1,x2,…,xq,rx)•(10q-1,-1);

}

}

在Gcoset的分布式路由算法中，假设当前结点为v，如果它的下一步结点出现故障，随机选择结点v的其他邻居作为下一步结点，由算法2继续进行路由选择，最终到达目标结点.因此，Gcoset拥有度数较小、路由算法简单、容错性能良好的性质，同时还具有路径长度短和聚集系数较大的小世界网络的特性.下文将基于Gcoset来构造GDCN的拓扑.

3 Gcoset图在DCN中的应用

3.1 GDCN拓扑

GDCN是用较小网络替代Gcoset图中的结点，构建出的更大网络.在GDCN网络中，用于替代Gcoset图中的结点的网络称为因子网络(也被称为簇).由于Gcoset图中有q×2q个结点，因此在GDCN中共有q×2q个簇，每个簇可以由一个交换器和若干服务器连接组成，也可以是数据中心中若干个交换器和若干服务器连接组成.下面介绍由GDCN构成的一种具体的DCN.

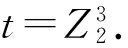
(1)(ch,rh)=(cg,rg)•s，s∈S.

(2)若s=(0q,1)，则tg=000,th=001;

若s=(0q,-1)，则tg=001,th=000;

若s=(0q,2)，则tg=010,th=011;

若s=(0q,-2)，则tg=011,th=010;

若s=(0q-11,1)，则tg=100,th=101;

若s=(10q-1,-1)，则tg=101,th=100;

若s=(0q-211,2)，则tg=110,th=111;

若s=(110q-2,-2)，则tg=111,th=110.

图2为结点(0q,0)中的服务器与簇外服务器的连接情况.为了描述方便，将与服务器g连接的簇外服务器h的条件简记为h=g•s.

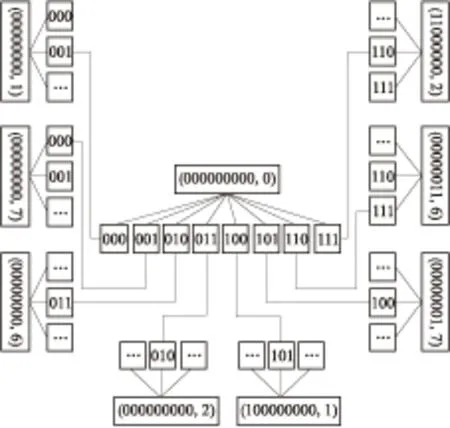
图2 结点(0q,0)中的服务器与簇外服务器的连接情况

Fig.2 Servers’ link between vertex(0q,0)and other clusters

3.2 GDCN容错路由

在数据中心网中，链路错误是不可避免的，因此必须通过路由算法保证在链路失效时仍然可以实现数据包的转发.在数据中心网中，有3种失效类型：链路失效、服务器故障和交换机故障.为了及时发现失效设备，服务器应周期地向外发出查询数据包以获知相邻服务器的状态.对于一台服务器来说，链路失效的结果直接表现为无法收到相邻服务器或所连接交换机的响应数据包，因此，可以将链路错误根据情况视为服务器故障和交换机故障处理.考虑到失效顶点的问题，在选择下一跳前，调用函数GetReachable()探测下一跳顶点是否可达，如果不可达，算法会选择另一个正常的邻居顶点，当然，在这种情况下路由长度有一定的增长.GDCN的容错路由算法(记为算法3)如下文所示.

输入：当前服务器g=(x1,x2,…,xq,rx,tx)，目的服务器h=(y1,y2,…,yq,ry,ty)

输出：下一跳的标识符

if((x1,x2,…,xq)=(y1,y2,…,yq)andrx=ryandtx=ty)

the destination has been reached.

else if((x1,x2,…,xq)=(y1,y2,…,yq) andrx=ry)

return GetReachable((x1,x2,…xq,rx,ty))

else{

Δr=(8+ry-rx)mod 8;

if((x1,x2,…,xq)=(y1,y2,…yq)){

if(Δr=1)

return GetReachable(g•(0q,1));

else if(Δr<=4)

return GetReachable(g•(0q,2),g•(0q,1));

else if(Δr<7)

return

GetReachable(g•(0q,-2),g•(0q,-1));

else if(Δr=7)

return GetReachable(g•(0q,-1));

}

else{

∥(y1,y2,…,yq)循环左移Δr位

(z1,z2,…,zq)=(y1,y2,…,yq)<<<Δr;

if(x1=z1andx2=z2)

return

GetReachable(g•(0q,-2),g•(0q,-1));

else if(x1=z1)

return GetReachable(g•(0q,-1));

else if(x1≠z1andx2≠z2)

return

GetReachable(g•(110q-2,-2),g•(10q-1,-1));

else if(x1≠z1)

return GetReachable(g•(10q-1,-1));

}

}

4 GDCN与其他DCN模型的比较

数据中心的规模在不断扩展， DCN模型的可扩展性也得到极大的关注.有些模型的可扩展性受服务器和交换机的端口数的限制.在DCN模型中，交换机数量对构建数据中心网络的影响比较大，不同的DCN模型，所需交换机数量差异也比较大.

从表1可以看出，GDCN的可扩展性不受服务器端口数目的限制，Fat-Tree和FiConn也具有同样的优势，但是服务器端口数目将影响Dcell和Bcube的可扩展性.与Dcell、Bcube和FiConn一样，交换机端口数目对GDCN的可扩展性没有影响，但是Fat-Tree受交换机端口数目的影响.在构建GDCN时，所需要的交换机数据也是比较少的.综上所述，GDCN结构简单，通信性能较高，可扩展性和容错性也比较好，使得它适合于大规模数据中心网络的构建.

表1 Fat-Tree、DCell、BCube、FiConn和GDCN模型的比较

5 结语

文中基于代数图方法构造了一个数据中心网GDCN，网络静态拓扑模型为8度正则度，从而具有更好的对称性和简单的结构；此外，GDCN的网络直径仅为O(logN)，具有较简单的路由算法和良好的路由容错性,还具备了良好的小世界网络特性.今后将对GDCN的小世界网络特性和对称性质做进一步的研究,并利用这些性质开发组播、负载均衡和内容分发等应用.

[1] AHMED F,MANNHEIM H.Amazon elastic compute cloud (Amazon EC2) [OL].(2008- 12- 10) [2016- 07- 12].http:∥aws.amazon.com/ec2/.

[2] CARR D.How Google works [OL].(2006- 07- 06) [2016- 07- 12].http:∥www.baselinemag.com/c/a/Infrastructure/ How-Google-Works-1.

[3] DEAN J，GHEMAWAT S.MapReduce:simplified data processing on large clusters [J].Communications of the ACM，2008，51(1):107- 113.

[4] HOFF T.Google architecture [OL].(2008- 11- 22) [2016- 07- 12].http:∥highscalability.com/google-architecture.

[5] RABBE L.Powering the Yahoo! network [OL]. (2006- 11- 27) [2016- 07- 12] .http:∥yodel.yahoo.com/2006/11/ 27/powering-the-yahoo-network.

[6] ZHANG Y，ANSARI N.On architecture design，congestion notification，TCP incast and power consumption in data centers [J].IEEE Communications Surveys & Tutorials，2013，15(1):39- 64.

[7] 魏祥麟，陈鸣,范建华,等.数据中心网络的体系结构 [J].软件学报，2013,24(2):295- 316.

WEI Xiang-lin,CHEN Ming,FAN Jian-hua,et al.Architecture of the data center network [J].Journal of Sofware,2013,24(2):295- 316.

[8] LI D，WU J.FCell:towards the tradeoffs in designing data center network architectures [C] ∥Proceedings of the 24th International Conference on Computer Communication and Networks (ICCCN).Las Vegas:IEEE，2015:1- 8.

[9] LI D，WU J.Dual-centric data center network architectures [C]∥Proceedings of the 44th International Confe-rence on Parallel Processing.Piscataway:IEEE Communications Society，2015:679- 688.

[10] BARI M F，BOUTABA R，ESTEVES R，et al.Data center network virtualization:a survey [J].IEEE Communi-cations Surveys & Tutorials，2013，15(2):909- 928.

[11] AL-FARES M，LOUKISSAS A，VAHDAT A.A scalable，commodity data center network architecture [J].ACM SIGCOMM Computer Communication Review，2008，38(4):63- 74.

[12] GUO C，WU H，TAN K，et al.Dcell:a scalable and fault-tolerant network structure for data centers [J].ACM SIGCOMM Computer Communication Review，2008，38(4):75- 86.

[13] GUO C，LU G，LI D，et al.BCube:a high performance，server-centric network architecture for modular data centers [J].ACM SIGCOMM Computer Communication Review，2009，39(4):63- 74.

[14] LI D，GUO C，WU H，et al.FiConn:using backup port for server interconnection in data centers [C]∥Pro-ceedings of the INFOCOM 2009.Piscataway:IEEE，2009:2276- 2285.

[15] WATTS D J，STROGATZ S H.Collective dynamics of ‘small-world’networks [J].Nature，1998，393(6684):440- 442.

[16] SHIN J Y，WONG B，SIRER E G.Small-world datacen-ters [C]∥Proceedings of the 2nd ACM Symposium on Cloud Computing.New York:ACM，2011:1- 13.

ANovelStructuredDataCenterNetworkwithConstantDegreeandSmall-WorldCharacteristics

LIMei-sheng1,2XIAOWen-jun3LAIZheng-wen1ZHANGZhan-ying1HANDong2

(1. School of Computer Science and Engineering, South China University of Technology, Guangzhou 510006, Guangdong, China;2. Department of Internet Finance and Information Engineering, Guangdong University of Finance, Guangzhou 510520, Guangdong,China;3. School of Software Engineering, South China University of Technology, Guangzhou 510006, Guangdong, China)

Firstly, Gcoset, an algebraic graph with constant degree, is defined. Secondly, on the basis of Gcoset, a virtualized topology structure named GDCN, which is of eight-degree regularity and symmetry for data center network, is proposed. Then, the static model of GDCN and the routing algorithm of GCoset are both described in detail, and a concrete implementation of GDCN is presented. Finally, a comparison between GDCN and other data center network models is made. The results show that GDCD is of a network diameter of onlyO(logN) and needs relatively simple routing algorithm, and that it possesses simple structure, high communication performance, good scalability and excellent fault tolerance.

constant degree; data center network; small-world characteristic; virtualization; topology structure; routing algorithm

2017- 01- 16

国家自然科学基金资助项目(61170313，61103037,61370003)

*Foundationitems: Supported by the National Natural Science Foundation of China(61170313,61103037,61370003)

李梅生(1975-),男,博士生,讲师，主要从事数据中心网络、复杂网络研究.E-mail:meisen04@163.com

†通信作者: 肖文俊(1950-),男,教授,博士生导师,主要从事互连网络、网络虚拟化研究.E-mail:2259975946@qq.com

1000- 565X(2017)07- 0063- 06

TP 393

10.3969/j.issn.1000-565X.2017.07.009