基于遗传算法的锂离子电池等效电路参数识别
2017-12-15,,
,,
(湖北大学 计算机与信息工程学院物联网工程研究所,武汉 430062)
基于遗传算法的锂离子电池等效电路参数识别
姚静,虞随,胡婧昕
(湖北大学计算机与信息工程学院物联网工程研究所,武汉430062)
结合锂离子电池双极性等效电路模型提出了一种基于遗传算法的参数识别方法,该方法通过指数函数对电路模型中的电阻、电容、恒压源等元件进行有理逼近,根据电池在不同充放电速率下的输出电压特性数据,通过实数编码遗传算法得到最优的函数参数,从而得到最优的电阻、电容,开路电压等电路参数值,针对电池在不同的工作状态,不同的工作参数下的运行数据,系列仿真和实验结果表明该算法原理简明,收敛较快,辨识得到的最优模型其电压输出特性与电池的实际电压输出特性基本吻合,能较精确的反映电池的实际特性,具有较高的辨识精度。
遗传算法;参数识别;锂离子电池;等效电路
0 引言
电动汽车具有高能效、低排放的特点,目前受到业界关注,得到了大力发展。锂离子电池作为电动汽车的主要能量来源,是电动汽车的关键部位之一,其特性直接影响电动汽车的性能,电池等效电路模型是电池荷电状态估计、性能分析、科学评价、高效管理和使用的基础,是从电池外部特性分析内部状态的有效手段,精确的电池等效电路模型对动力电池仿真、优化和能量管理有重要意义。
目前研究人员已建立了多种可对电池性能进行全面描述的等效电路模型,等效电路模型的精确性很大程度上取决于参数辨识精度。常用的电路参数辨识方法有最小二乘法,极大似然估计法和Kalman滤波法[1-3]。本文提出一种遗传算法对电池等效电路模型的参数进行优化,得到最优的电池等效电路模型参数,算法原理简明,收敛较快,获得的电路模型精度高,为电池性能分析和管理提供了重要依据。
1 锂离子电池等效电路模型
电池等效电路模型使用电阻、电容、恒压源等电路元件组成电路网络来模拟电池的动态特性与其它性能,由等效电路模型可以得到电路时域解析方程,便于分析与应用,因此广泛用于电动汽车功率系统仿真和电池管理系统中。目前研究的电池等效电路模型有Rint模型、RC模型、Thevenin模型、PGNV模型[4-5]。Thevenin模型在某种程度上能模拟锂离子电池的极化特性,但实验发现锂离子电池具有明显的双极化特性,为了提高等效电路在充放电结束时刻的精度,将电池的电化学极化特性与浓差极化特性分别表示,一个改进的双极化等效电路模型[6]如图1所示。

图1 双极性等效电路模型
双极化等效电路模型有3部分组成:1)开路电压UOC;2)内部阻抗:R0为欧姆电阻;Rpa为浓差极化电阻;Rpc为活化电阻;3)有效电容:Cpa和Cpc用来模拟两种极化特征的瞬态特性。该电路模型可由如下电路方程描述:
(1)
式中,Upa和Upc分别是电容Cpa和Cpc两端的电压;Il为流过电阻R0的电流;Ul为电池两端的输出电压。上面电路方程可得输出电压表达式如下:
Ul=UOC-IlR0+Upa(0)e-t/RpaCpa+Upc(0)e-t/RpcCpc
-IlRpa(1-e-t/RpaCpa)-IlRpc(1-e-t/RpcCpc)
(2)
其中:Upa(0)和Upc(0)为电容两端的初始电压,可由下式求得:
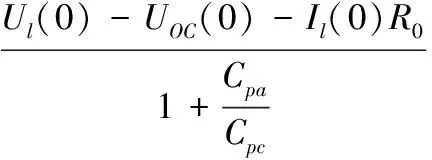
(3)

(4)
电池产品目录提供了电池在不同的充放电速率下,荷电状态SOC在区间(0,1)之间变化时SOC-Ul曲线,利用该曲线数据通过遗传算法辨识出电路中的元件参数,目标是使输出电压模型计算值与实验值之间的误差最小。电路参数随SOC的变化而变化,文献中有多种描述电路参数的解析函数,研究发现指数形式的解析函数辨识出的参数具有更高的精度[7],这里选用式(5)所示函数对电路参数进行有理逼近,k0-k20为21个需要辨识的模型参数。
R0=k0e-k1 soc+k2
Rpa=k3e-k4 soc+k5
Cpa=k6e-k7 soc+k8
Rpc=k9e-k1 0 soc+k11
Cpc=k12e-k13 soc+k14
UOC=k15e-k16 soc+k17+K18SOC+K19SOC2+K20SOC3
(5)
2 基于遗传算法的电路参数识别
遗传算法通过模拟自然界优胜劣汰的进化原则,在解空间范围内搜索出最优的个体,具有全局搜索能力强,鲁棒性高和通用性好等优点,被广泛应用于系统优化,自适应控制,模式识别以及参数识别中[8]。
遗传算法应用于参数识别时,首先将参数的搜索空间映射成遗传空间,每一组可能的参数值为解空间内的一个染色体或个体,其中任何一个参数称为基因,采用合适的编码方式对基因编码,然后设定种群规模,随机产生初始种群,对所有个体进行评价,按照适者生存、优胜劣汰的原理,通过遗传操作,逐代演化产生出越来越好的近似解,最终得到最优参数值[9]。
2.1 编码方法
需要识别的参数值[k1,k2,k3…,km]是一个多维、连续变化的量,这类优化问题实数编码方式处理起来更加方便有效,将k=[k1,k2,k3…,km]定义为解空间内的一个染色体或个体,这里k为一个m维向量(m为参数个数),其中任何一个参数ki称为基因,基因采用实数编码的方法,各参数的具体取值作为基因个体,参数的取值范围即为问题的搜索空间:[k1min,k2min,k3min…,kmmin]- [k1max,k2max,k3max…,kmmax]。
2.2 适应值函数
等效电路模型最优参数识别的目标是根据实验数据得到最优的电路参数,使输出电压模型计算值与实验值之间的误差最小。Ul为模型计算所得到的输出电压值,Uc为电池厂家提供产品样本输出电压值,取样点数为n,则目标函数如下:
f=|Uc-Ul|1+|Uc-Ul|2+…+|Uc-Ul|n
(6)
f的值越接近于零则模型曲线与产品样本曲线越接近,则模型的精度越高,负的电压值是不允许出现的,所以任何一套参数k0-k14都要保证计算所得的电压值为正,即Ulj≥0,Uocj≥0(j=1,2, …,n)。该问题是一个带约束条件的优化问题,个体约束违反值为:
(7)
将约束条件转化为惩罚函数,建立适应度函数如下:

(8)
式中:A为惩罚系数;f为误差函数;AfViop为惩罚函数,保证了结果满足输出电压和开路电压为正。f+Afviop越小说明模型精度越高,对应适应度函数值就越大,这样的个体就越优秀。
2.3 遗传操作
遗传算法通过3个基本操作:选择、交叉和变异来产生新的后代,从而实现个体的繁殖与进化。
1)选择。
选择是指从群体中挑选出优秀的个体,淘汰掉劣质个体的方法。比较常见的选择方法有如下几种:比例选择、排序选择、精英选择。这里采用排序选择与精英保留相结合的方法。根据群体的适应值,首先挑选最优个体直接保留作为下一代,其它个体按照它们适应值的大小降序排列,根据他们在群体中的排名来分配选择概率,排名在前面的个体有更大的概率被选中,再采用轮盘赌法按分配的概率进行选择。各个体的选择概率按下式计算。

(9)

(10)
式中,i为个体在群体中的排名,prob(i)为排名为i的个体的选择概率,q为通过比例选择法得到的最差个体的选择概率,N为种群中个体的数目。
2)交叉。
交叉操作是将被选中的个体部分基因进行交换,从而生成新的个体,交叉操作使个体不断进化,对于实数编码方式,通常采用算术交叉算子来进行交叉运算,如下式所示:
(11)
式中,k1t和k2t为父代中被选中的两个个体,a为一系数,取值在(0,1)之间随机产生,k1t+1和k2t+1为交叉后生成的子代个体。
为了提高算法的收敛速度,采用自适应的交叉概率,在算法执行初期,个体远离全局最优解,这时交叉概率取值相对较大,随着进化代数的增加,搜索结果越来越接近全局最优解,这时交叉概率取值相对较小,这样更有利于保留种群中的优良个体基因,从而提高收敛速度,交叉概率函数如下式:
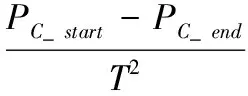
(12)
式中,PC(t)表示第t代交叉概率;PC_start表示进化开始时的交叉概率;PC_end表示迭代过程结束时的交叉概率;T为设定的迭代终止次数;t为正在进行的迭代次数。
3)变异。
变异操作模拟生物进化过程中的基因突变过程,在一定程度上可以增加种群的多样性,避免搜索陷入局部最优,本文选用固定变异概率,均匀双向变异算子进行变异操作,表示如下:
(13)
式中,kit为变异点原来的值,kit+1为变异点的新值,kimin和kimax为参数ki取值上下限,c、w为0~1间的随机数。
算法执行流程如图2所示。

图2 遗传算法参数识别流程图
3 实例仿真与分析
电池ePLB是一种聚合物锂离子电池,具有能量密度高,体积小,安全性高和成本低等优势。选用该电池为实验对象,在电池充电和放电两种情况下,对给定的产品样本输出电压曲线进行数据提取,取样点数n=22,采用双极性等效电路模型,应用遗传算法来识别电路模型参数k0-k20,然后将得到的最优等效电路模型的电压输出特性与电池厂商提供的样本特性进行比较。
3.1 充电状态
分别取充电速率Cr=0.5C,Cr=4C(C=8A),利用遗传算法得到该等效电路模型的最优模型参数,结果如表1所示。
在22个取样点位置,最优模型电压输出值与产品目录电压输出值可表示为图3、图4,从图中可以看出充电状态下两者的电压输出值几乎完全重合,说明遗传算法得到的最优解接近全局最优,求解精度高,误差小。
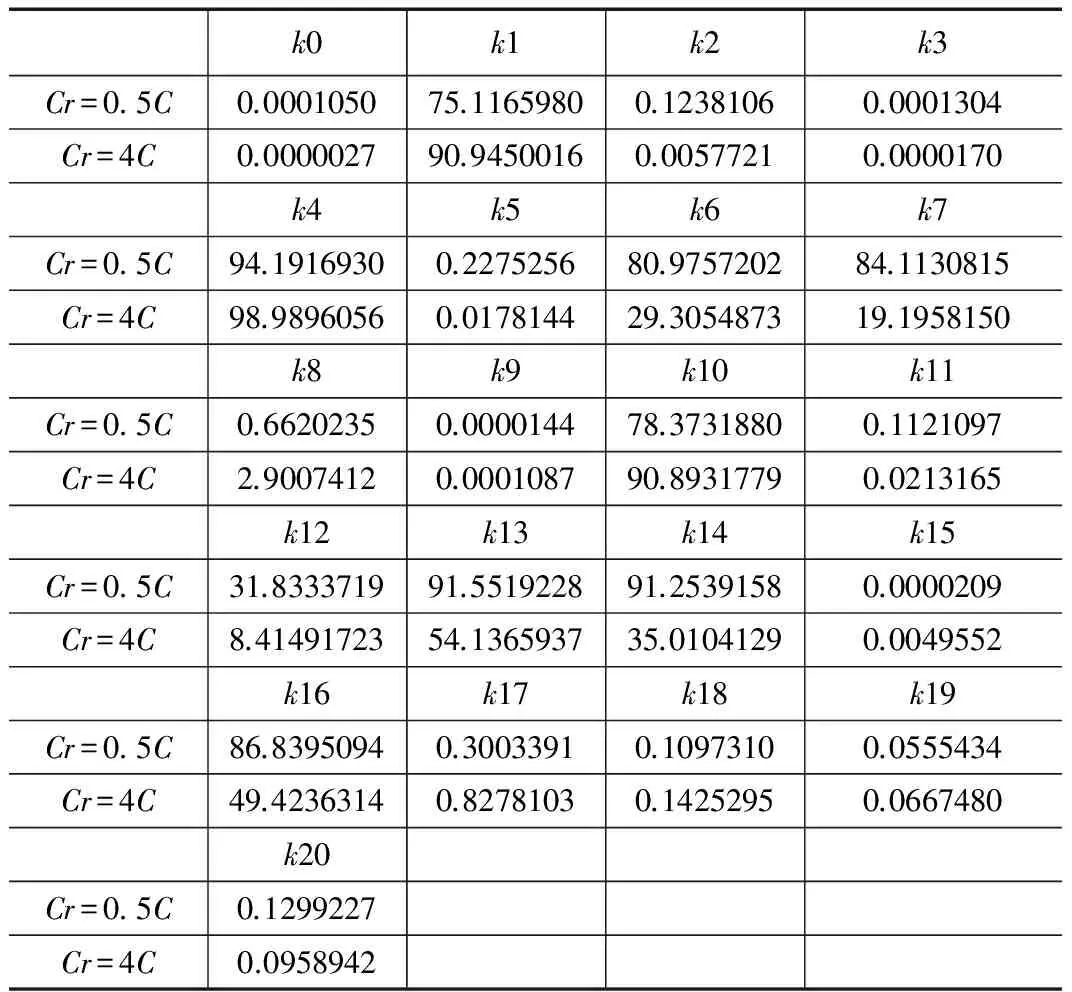
表1 充电状态最优参数

图3 Cr=0.5C充电过程采样点输出电压比较

图4 Cr=4C充电过程采样点输出电压比较
为了进一步证明最优电路模型的精确性与适用性,在电池样本输出电压特性曲线上提取25个与前面数据不重合的数据点,利用前面得到的最优电路参数,利用式(2)计算输出电压值,拟合得到最优模型输出电压曲线,将该曲线与电池实际输出电压曲线进行比较,结果如图5、图6所示。

图5 Cr=0.5C充电过程输出电压特性比较
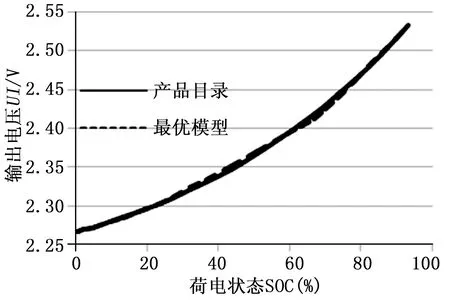
图6 Cr=4C充电过程输出电压特性比较
从图中可以看出,电池充电状态下,通过遗传算法识别出的等效电路模型,其输出电压与荷电状态的关系曲线与电池生产厂商提供的电压输出特性曲线完全吻合,说明该电路模型能反映电池的实际输出特性。
3.2 放电状态
分别取放电速率Cr=0.5C,Cr=10C(C=8A),利用遗传算法得到该等效电路模型的最优模型参数,结果如表2所示。

表2 放电状态最优参数
在22个取样点位置,最优模型电压输出值与产品目录电压输出值可表示为图7、图8,从图中可以看出电池在放电状态下,通过遗传算法识别出的电路参数也具有很高的精度。

图7 Cr=0.5C放电过程采样点输出电压比较
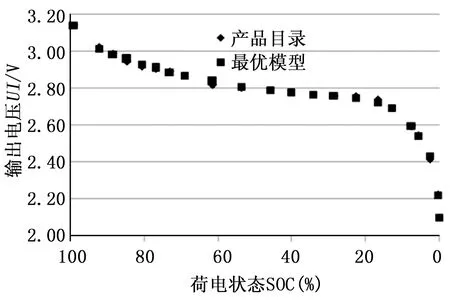
图8 Cr=10C放电过程采样点输出电压比较
为了证明放电状态下通过上面的方法建立的电池等效电路模型的有效性,分别在两种放电速率下另取25个采样点,利用算法得到的电路参数来计算电池输出电压,拟合得到输出电压动态曲线,如图9、图10所示。

图9 Cr=0.5C放电过程输出电压特性比较
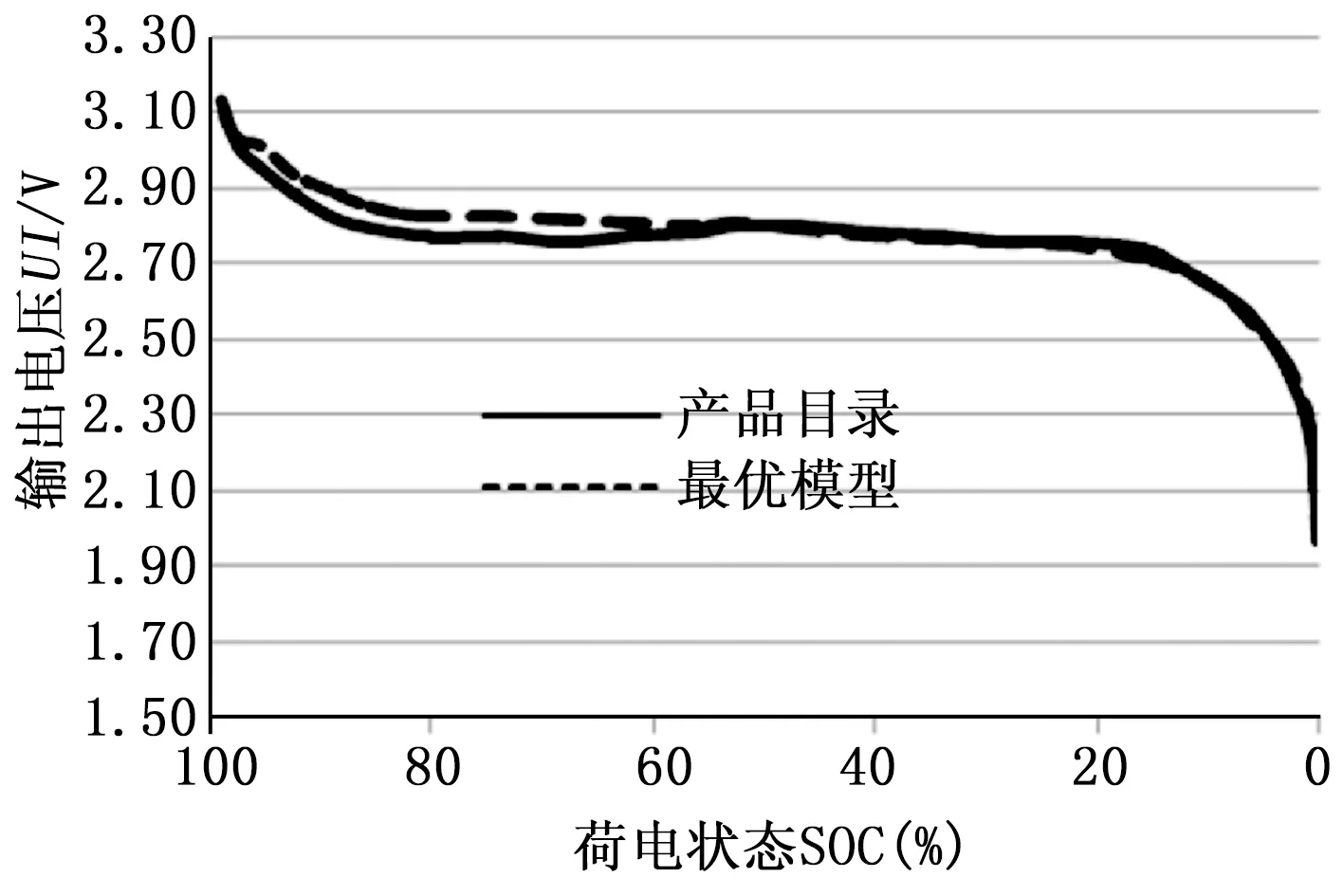
图10 Cr=10C充电过程输出电压特性比较
从图中可以看出,电池放电状态下,通过遗传算法识别出的等效电路模型,其输出电压与荷电状态的关系曲线与电池生产厂商提供的电压输出特性曲线基本吻合,其误差比充电状态稍大,但能基本反映电池的实际输出特性。
4 结语
本文提出一种基于遗传算法的电池等效电路模型参数识别方法,根据电池非线性双极性等效电路模型,利用电池输出电压特性数据,通过实数编码遗传算法辨识最优的电路参数。针对电池在不同的工作状态,不同的工作参数下的运行数据,系列仿真和实验结果表明遗传算法辨识得到的最优模型其电压输出特性与电池的实际电压输出特性基本吻合,能较精确的反映电池的实际特性,具有较高的辨识精度。
[1] 陈大分,姜久春,王占国,等. 动力锂离子电池分布参数等效电路模型研究[J]. 电工技术学报,2013,7(28):169:176.
[2]冯旭云, 孙泽昌, 高卫民,等. 镍氢动力电池电荷状态估计算法仿真研究[J]. 系统仿真学报, 2010,7(22): 1585-1591.
[3]魏学哲,孙泽昌,田佳卿. 锂离子动力电池参数辨识与状态估计[J]. 同济大学学报,2008,2(36):231-235.
[4]林成涛,仇 斌,陈全世. 电流输入电动汽车电池等效电路模型的比较[J]. 机械工程学报, 2005,12(41):76-81.
[5]Hongwen He, Rui Xiong, Jinxin Fan. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach [J]. Energies, 2011,4:582-598.
[6]Krishnan S. Hariharan, V. Senthil Kumar. A nonlinear equivalent circuit model for lithium ion cells[J]. Journal of Power Source, 2013(222):210-217.
[7]吕 超,刘珊珊,沈 杰,等.锂离子电池等效电路模型的比较研究[J]. 电源技术应用,2013,11:158-164.
[8]边 霞, 米 良. 遗传算法理论及其应用研究进展[J]. 计算机应用研究, 2010,7(27):2426-2428.
[9]冯长辉, 齐晓慧, 苏立军,等. 基于遗传算法的四旋翼无人机系统参数辨识[J]. 计算机测量与控制, 2015, 23(12):4195-4197.
ParameterIdentificationofLithium-IonBatteryEquivalent-CircuitModelBasedonGeneticAlgorithm
Yao Jing, Yu sui, Hu Jingxin
(Institute of Internet of Things, School of Computer Science and Information Engineering,Hubei University, Wuhan 430062, China)
On account of lithium-ion battery dual polarization (DP) equivalent circuit model a genetic algorithm is proposed for parameter identification. The method makes resistance, capacitance and open circuit voltage source in the circuit model as exponential function based rational approximant. According to the characteristic data of output voltage in different charge and discharge rate, A real code genetic Algorithm (GA) is employed to estimate the battery model parameters including the resistance, capacitance and open circuit voltage. The algorithm is applied to several cases in different working conditions and working parameters. The simulation and experimental results demonstrate that the genetic algorithm to identify the parameters has concise principle and quickly convergence. The equivalent circuit model with the optimally extracted parameters can accurately predict the performance of the lithium-ion battery and has high identification precision.
genetic algorithm; parameter identification; lithium-Ion batteries; equivalent circuit Model
2017-09-11;
2017-10-11。
姚 静(1976-),女,湖北天门人,博士,讲师,主要从事智能优化算法方向的研究
1671-4598(2017)11-0252-05
10.16526/j.cnki.11-4762/tp.2017.11.064
TP391.9
A
