基于粒子群的高超声速飞行器闭环制导研究
2017-12-15,,,,
, ,,,
(中国兵器工业第203研究所,西安 710065)
基于粒子群的高超声速飞行器闭环制导研究
王荔豪,杨凯,曹小斌,王妮芝,马菲
(中国兵器工业第203研究所,西安710065)
高超声速飞行器一般指的是在大气层内以大于5马赫数的速度飞行的一类飞行器;对于高超声速飞行器的研究来说,凭借其超高的飞行速度和飞行高度,能够在短时间内飞行更远的距离;为了达到作战要求,需要规划整个飞行轨迹,而最为重要的便是上升段的制导问题;以X-33高超声速飞行器模型为研究对象,提出基于粒子群算法的闭环制导策略,通过导航系统测量计算得到飞行器的速度增量等飞行参数,同时解算速度和高度等信息,机载计算机根据制导算法在每一个制导周期内在线生成制导指令,实时修正飞行轨迹,使飞行器最终准确到达目标位置;并对该方法的可靠性进行了仿真验证;仿真结果表明,基于粒子群算法的闭环制导策略优化精度高,物理概念明确,能满足高超声速飞行器上升段的闭环制导需求。
高超声速飞行器;粒子群;目标函数;闭环制导
0 引言
高超声速飞行器一般是指飞行速度大于5马赫的飞行器,常飞行于20 km到150 km的临近空间区域。飞行器由助推级推至预定高度,然后滑翔弹头依靠气动升力实现远距离的非弹道式飞行,这样能够快速有效地打击远程目标,实现精确打击的目的[1-2]。
文献[3]对传统的开环制导方式进行了研究,预先在地面离线为飞行器设计一条理想的飞行轨迹,在实际飞行器中不断调整姿态,使真实轨迹始终处于理想轨迹附近。但是这种方法在存在强烈外界干扰时无法跟踪预定轨迹。
文献[4]使用定点迭代法应用于闭环上升段制导。固定大气段终端节点的初始猜想位置,通过真空算法得到相应的伴随状态作为大气段的终端约束,为了求得最优解,进行反复迭代。但是该过程需要依靠人为经验来设定,因此无法保证在任何条件下都具有相同的收敛性。
本文提出基于粒子群算法的高超声速飞行器上升段闭环制导方法,并对其可靠性进行仿真验证,本文的研究结果为高超声速飞行器的闭环制导提供了有价值的参考。
1 上升段建模
1.1 质心运动及动力学方程
高超声速飞行器运动方程组是描述作用在飞行器上的力、力矩与飞行器运动参数之间关系的一组方程。它由飞行器质心运动和姿态变化的动力学方程、运动学方程、质量变化方程、角度几何关系方程和描述控制系统工作的方程所组成。
在初步设计阶段,为了能够简捷地获得飞行器的飞行轨迹,暂不考虑飞行器绕质心的转动,将其作为一个可操纵质点进行轨迹优化。简化之后的飞行器运动方程组由质心动力学方程、运动学方程和质量变化方程组成。飞行器爬升平面内运动方程组为:
(1)
式中,T为飞行器所受推力大小,D为飞行器所受阻力大小,L为飞行器所受升力大小,H为飞行器的飞行高度,V为飞行器的飞行速度,为高超声速飞行器质量,Isp为燃料比冲,g0为海平面重力加速度,α和θ分别为飞行器的攻角和弹道倾角,q为俯仰角速度[5]。
1.2 气动力模型
为避免复杂的插值运算,采用曲线拟合方法处理高超声速飞行器的气动力系数和发动机推力系数。曲线拟合方法不要求所拟合的曲线通过节点,而要求在所考虑的区域内均方差尽可能小。
选取攻角α和马赫数M作为影响气动力的最主要因素,拟合公式能提高算法快速性,气动力模型如下:
(2)
该模型为非线性模型,采用最小二乘法进行参数辨识。参数辨识结果为:
(3)
气动力系数拟合曲线如图1所示。
1.3 发动机推力模型
本文采用涡轮发动机与超燃冲压发动机相结合的推力模型作为研究对象[6]。发动机推力系数CT随着飞行器飞行高度H、马赫数M和攻角α的变化而变化,根据实验所得数据进行曲线拟合,得到推力系数的计算公式:
CT(M,α)=
(4)
2 上升段约束条件
2.1 微分方程约束
将前文推导的运动及动力学模型、气动系数模型、推力模型代入到飞行器的质心运动方程组中,得到高超声速飞行器上升段状态方程的微分约束:
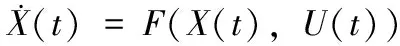
(5)
式中,X(t)是由飞行器上升阶段5个状态量组成的向量,U(t)是攻角控制量α。
X(t)=[H(t),x(t),V(t),θ(t),m(t)]
(6)
U(t)=α(t)
(7)
2.2 状态量和控制量约束
控制能力约束主要反映到可使用攻角的约束,对应的控制量U(t)必须限制在一定范围内[7];据此建立如下约束条件:
(8)
2.3 边值约束
初始边界条件:
H(t0)=H0,V(t0)=V0,θ(t0)=θ0
(9)
终止边界条件:
H(tf)=Hf,V(tf)=Vf,θ(tf)=θf
(10)
其中,t0和tf分别为爬升段的初始时刻和终止时刻。
2.4 路径约束
2.4.1 热流约束
在飞行器爬升过程中,由于大气与机体的摩擦会导致机体表面温度升高,一旦飞行器表面温度高出其表层防热材料的允许值,就会对飞行器造成不可逆的损坏,甚至有可能影响飞行任务的完成[7]。工程应用中,热流密度表达式为:
(11)
式中,
C=7.9686×10-5,N=0.5,K=3.15
(12)
2.4.2 动压约束
飞行器的气动铰链力矩和飞行器表面的防热材料限制了动压的上限,动压约束的下限值主要与超燃冲压发动机启动的要求相关。
因此,根据任务要求,考虑动压对控制系统的影响,存在动压约束:

(13)
2.4.3 过载约束
由于本文研究的是高超声速飞行器的上升阶段,所以只对飞行器纵向平面进行分析,此处过载约束为飞行器的最大法向过载约束,即:

(14)
2.5 目标函数
在飞行器上升段轨迹优化末端,已不再具有爬升趋势,此时有θ(tf)≈0°。末端速度Vf和末端高度Hf是需要优化设计的,也就是使飞行器到达末端任务点时,能够尽可能地接近任务终端速度Vαscent和高度Hαscent,因此定义目标函数J为:
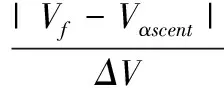
(15)
式中,wV和wH为分别飞行末端速度和高度偏差的加权系数,ΔV和ΔH分别为末端允许的高度和速度偏差范围。为简化工程上多目标优化的处理,本文采用了权重和法来对飞行末端高度和速度参数进行优化,通过调整加权系数可以方便地改变飞行末端速度和高度在轨迹优化过程中所占的权重比例。
2.6 上升段飞行走廊
基于上节提出的高超声速飞行器上升阶段需要满足的约束条件,由于飞行器将在大气层内飞行一段距离,为了使飞行器能够安全稳定地进行上升飞行,需要对飞行器的飞行状态进行约束控制,使其飞行过程中的状态变量在动压、过载以及热防护结构所允许的范围之内。通过对动压上下限、热流密度上限以及状态量的上下限的确定,这些条件共同确定了高超声速飞行器上升阶段的可飞行区域,形成飞行器上升段飞行走廊。

图2 上升段飞行走廊
由约束条件中的最大动压和最小动压条件限制了高度范围,图中方框显示的区域是由高度和速度的上下限确定的。当飞行器能够满足动压约束时,自然就满足了热流约束。因此上升段的飞行走廊主要由飞行器的动压约束条件来确定的,它和高度-速度上下限共同组成了高超声速飞行器上升段的飞行走廊。
3 粒子群算法设计
3.1 轨迹参数规划策略
高超声速飞行器的上升阶段,其飞行过程较为复杂。在助推器与飞行器分离结束时刻,飞行器已经到达动力爬升段的初始点,在随后的飞行过程中,飞行器将开启自身发动机,继续向目标高度和目标速度飞行,以达到巡航飞行的要求指标。
高超声速飞行器在动力爬升阶段,推力线沿机体方向是固定的。当需要改变推力方向时,则需要调整飞行器的俯仰角,从而实现不同弹道倾角的爬升过程。在动力爬升段,飞行器的速度会迅速上升,同时会经过低空大气密度稠密区。在这个阶段最大热流和最大动压情况会出现。
通过给定最大动压和最大热流密度限制可以确定飞行轨迹的下边界,上升段的热流约束比较弱,而动压约束比较强,所以如果能满足动压约束,自然就能满足热流约束。
在高超声速飞行器的动力上升阶段,飞行器弹道倾角的选择直接影响到飞行任务终端的高度大小和速度大小,所以整个上升段的轨迹很大程度上取决于弹道倾角的选择[8-10]。如果采用较大的弹道倾角上升,会导致飞行器末端高度过高,且无法满足巡航阶段弹道倾角趋近于零的要求;若采用较小的弹道倾角,则动压会接近最大动压限制区域。
因此,本文在进行上升段轨迹优化设计时,采用一种分段弹道倾角的规划方法,这样可以避免上述问题,将上升段分为两段,具体策略如下:
1)第一段为恒定弹道倾角上升段。在低空稠密大气层内迅速爬升,避免动压超限,保持固定值一直到一定高度Hcenter;
2)第二段为变弹道倾角上升段。达到一定高度Hcenter后,此时按照弹道倾角线性减小的策略继续上升,当弹道倾角趋近于零时,飞行器高度和速度达到终端任务状态要求。按照线性减小弹道倾角的策略可以简化设计,易于实现。

(16)
3.2 算法流程
粒子群的个体代表问题的一个可能解,每个粒子都具有速度和位置两个定义,位置坐标对应的目标函数值作为该粒子的适应度,粒子群算法就是通过适应度来衡量某一粒子的优劣。以本文的研究对象来说,需要规划出飞行器上升阶段的弹道倾角和中间高度值,这两个参数分别代表两种粒子,通过每种粒子个体间的协作和竞争关系来寻求各自最优的解。首先对于弹道倾角和中间高度参数,初始化一群随机粒子,然后通过之前设定的边界条件,不断迭代得到最优解。在每一次的迭代过程中,粒子通过跟踪两个“极值来更新自己的位置和速度;粒子本身找到的最优解为个体极值;整个粒子群找到的最优解为全局极值。这样一步步迭代下去,最终满足精度的粒子即为最优弹道倾角值和最优中间高度值。
假设用xi表示第i个粒子,其中d为粒子的维数,某一粒子经历过的最好位置表示为pi,整个粒子群体经历过的最好位置表示为gi,第i个粒子的速度用vi来表示。在整个迭代过程中,第i个粒子根据如下式子来更新自己的位置和速度,表示为:
vid=wivid+c1×rand()×(pid-xid)+c2×
rand()×(gid-xid)
xid=xid+vid
(17)
粒子群算法的基本流程和制导系统流程图如图3和图4所示。

图3 粒子群算法流程图
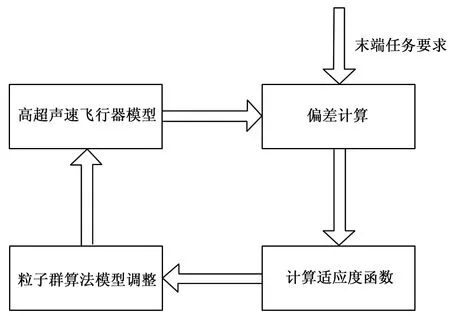
图4 制导系统流程图
对于基于粒子群的高超声速飞行器上升段闭环制导研究,本文选取的轨迹设计参数为[θpower,θcentre];同时,适应度函数是用来评价所设计轨迹的好坏,其表达式为:

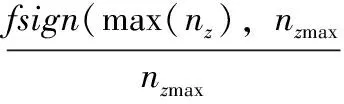
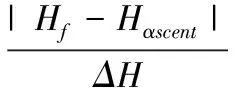
(18)
式中,wQ,wq和wnz分别为热流、动压以及法向过载的惩罚系数,wV和wH为任务末端的速度和高度的惩罚系数。速度允许偏差ΔV设定为100 m/s,高度允许偏差ΔH设定为500 m。同时,函数fsign定义为:
(19)
粒子群算法应用于高超声速飞行器轨迹优化是通过适应度函数的计算,对所需要设计的参数进行相应地调整,直至全局适应度值满足要求为止。
4 闭环制导策略
当助推器将飞行器送入指定高度后,助推器分离,开启自身发动机,进入动力爬升阶段,通过闭环制导策略达到预先设定的终端位置,满足随后巡航阶段的初始高度和初始速度要求。
如图5所示,高超声速上升段飞行器从起始位置开始,首先由轨迹优化算法为飞行器实时生成一条满足各种约束条件的最优轨迹,并将生成的攻角控制量传输给飞行器,随后飞行器的控制系统根据优化出的控制量控制飞行器近似地沿着最优轨迹运动。但是在飞行器实际飞行过程中下,会存在各种干扰情况,所以飞行器会在一段时间后偏离最优轨迹,到达中所示的A点。
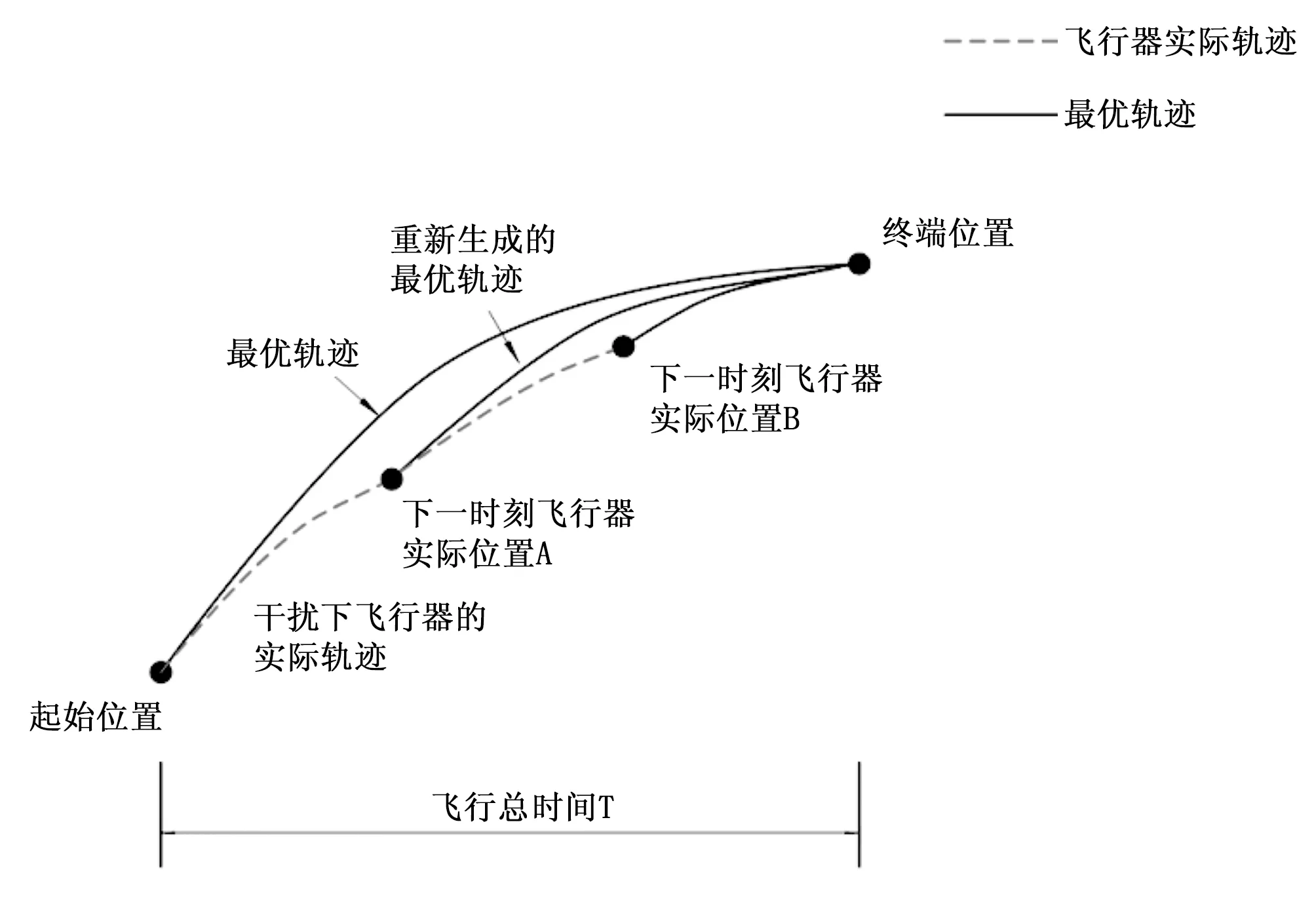
图5 闭环制导原理示意图
飞行器的惯导系统测量得到A点的真实状态参数,并以当前位置为初始位置,重新为飞行器生成一条从当前位置A点到终端位置的最优轨迹;在随后的飞行中重复上述过程,直至飞行器满足终端任务要求。
基于最优轨迹优化算法和上升段闭环制导的原理示意图,现提出高超声速飞行器上升段闭环制导的结构框图,如图6所示。整个闭环制导结构框图基本包含两个部分,分别为“最优轨迹生成”部分和“高超声速飞行器状态变量反馈”部分。
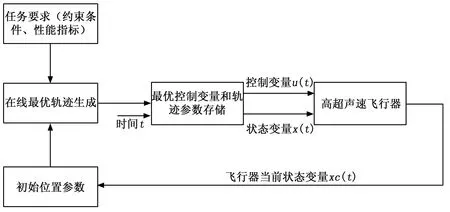
图6 闭环制导结构框图
本文所提出的高超声速飞行器闭环制导方式不仅能够实时地根据飞行器当前位置重新生成最优飞行轨迹,而且能够在飞行任务需要突然改变的情况下,重新更新任务要求(约束条件和性能指标),为飞行器重新生成最优轨迹。与传统的制导系统不同,该闭环制导系统包含了快速轨迹优化部分,提高了系统的自主性,保证高超声速飞行器在面临特殊环境和特殊任务时具有自主改变轨迹的能力。
5 仿真验证
5.1 仿真条件
首先对高超声速飞行器模型、上升阶段的初始参数以及约束条件、终端目标进行定义。
飞行器初始高度和初始速度:
(20)
终端高度和终端速度:
Vf=1900±100 m/s
hf=27±1km
(21)
路径约束参数如表1所示。

表1 路径约束条件
5.2 分析与验证
仿真过程分别采用开环制导和闭环制导方法进行分析比较。
5.2.1 开环制导
根据初始位置和终端位置,使用粒子群算法为高超声速飞行器优化出一条最优轨迹,优化出的最优轨迹参数:θpower=4.48°,Hcenter=20.078 km,将优化出的攻角指令带入飞行器的运动及动力学方程组中,即可得到开环制导方法下的飞行器实际飞行轨迹。
5.2.2 闭环制导
将飞行器整个飞行阶段分为n个周期,在每个周期过后粒子群算法会根据飞行器当前状态和终端任务在线实时优化出一条最优轨迹,飞行器将在某些干扰下按照不断生成的最优轨迹飞行。
对如下闭环制导仿真验证图中的线型进行说明:图中虚线表示的是每一个飞行周期为飞行器实时生成的最优轨迹总和;点线表示的是在开环制导方式下的飞行器飞行真实飞行轨迹;实线表示的是飞行器在整个周期内闭环制导方式下的实际飞行轨迹。
以阻力系数拉偏为例,对本文提出的闭环制导方法进行验证,对阻力系数拉偏+10%情况进行分析。仿真结果如图7~12所示。

图7 高度变化对比曲线
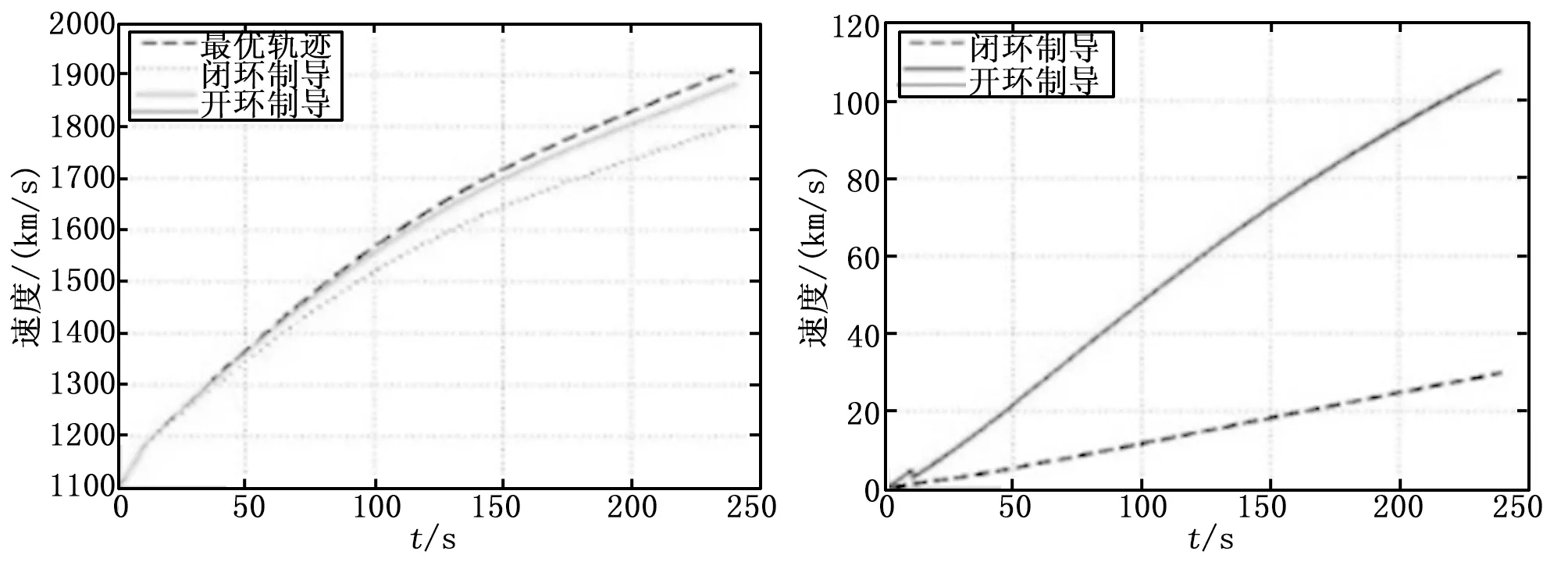
图8 速度变化对比曲线

图9 质量变化对比曲线

图10 动压变化对比曲线

图11 热流密度变化对比曲线

图12 过载变化对比曲线
在阻力系数拉偏+10%的干扰情况下,分析得出:
1)采用开环制导方式进行上升段飞行时,在阻力系数增加10%的情况下,高超声速飞行器的末端高度偏差约为140 m;而采用闭环制导方式,末端高度偏差为20 m,基本上与最优轨迹高度剖面重合。
2)从速度变化曲线可以看出,开环制导方式下的速度与终端任务速度偏差较大,约110 m/s,而闭环制导方式下的偏差为15 m/s。
3)从质量变化曲线可以看出,在阻力系数增加10%的情况下,开环制导方式下消耗的燃料比闭环制导方式以及最优轨迹方式消耗的燃料少,这也会影响飞行器的飞行速度和飞行高度无法满足要求。
4)由图10至图12可以看出,对于飞行过程的路径约束,闭环制导方式下飞行动压、热流密度和飞行过载均与最优轨迹曲线变化趋势一致,与最优轨迹的偏差比开环制导方式下的小,并且满足路径约束条件。
6 结论
本文针对高超声速飞行器上升段的飞行状态,提出基于粒子群算法的闭环制导策略,并建立了飞行器上升段的运动模型及约束条件模型。仿真结果表明,该闭环制导方法能够采用粒子群算法,根据飞行器当前状态量实时在线设计最优的飞行轨迹,以消除因为某些干扰因素对飞行器飞行轨迹造成的偏差,最终达到期望的终端目标。同时,该方法物理概念明确,高超声速飞行器终端偏差较小。
[1] 蔡亚梅. 美国的高超声速飞行器发展计划及关键技术分析[J]. 航天制造技术,2010(6):4-7.
[2] 王 威. 高超声速飞行器滑翔段制导方法研究[D]. 哈尔滨:哈尔滨工业大学,2010.
[3] 张四虎. 高超声速飞行器再入热环境分析及弹道优化设计[D]. 哈尔滨:哈尔滨工业大学,2013.
[4] Lu P, Sun H, Tsai B. Closed-loop Endo-atmospheric Ascent Guidance[J]. Journal of Guidance, Control and Dynamics,2003,26(2):283-294.
[5] 李新国,方 群. 有翼导弹飞行动力学[M]. 西安:西北工业大学出版社,2005.
[6] Chuang C H,Morimoto H. Periodic optimal cruise for a hypersonic vehicle with constraints[J]. Spacecraft Rockets,1997,34(2):165-71.
[7] 陈小庆,侯中喜,刘建霞. 基于直接配点法的滑翔轨迹快速优化设计[J]. 航空计算技术,2010(1):37-41.
[8] 泮斌峰. 吸气式空天飞行器闭环上升制导研究[J]. 飞行力学,2010(6):48-51.
[9] Peter A. Liever, Sami D. Habchi. Stage Separation Analysis of the X-43A Research Vehicle[Z].
[10] 祁 涛, 张彦斌. 基于遗传粒子群算法的模拟电路故障诊断方法研究[J]. 计算机测量与工程,2015(12):35-46.
ResearchonClosed-loopGuidanceforHypersonicVehiclesBasedonParticleSwarm
Wang Lihao,Yang Kai,Cao Xiaobin,Wang Nizhi,Ma Fei
(No.203 Research Institute of China Ordnance Industries, Xi’an 710065, China)
Hypersonic vehicle generally refers to a class of aircraft flying in the atmosphere with its Mach number greater than 5. In the process of research for hypersonic vehicle, the great long distance can be reached within short times due to its high flight speed and altitude. We need project the whole flight path in order to meet the operation plan. The most important part is the guidance problem of ascent stage. Taking X-33 aircraft model as the research object, and put forward the ascent closed-loop guidance of hypersonic vehicle based on particles swarm methods. The closed-loop guidance algorithm is called once every guidance update cycle to recalculate the optimal solution based on the current flight condition. It can correct the flight path in real time and lead the vehicle to the target location. Then simulate the reliability of this method. The result indicated that this closed-loop guidance method based on particle swarm has better accuracy, and the physical conception is specific. This method can satisfy the demand of closed-loop for the ascent of hypersonic vehicle.
hypersonic vehicle, particle swarm, objective function, closed-loop guidance
2017-04-17;
2017-05-15。
王荔豪(1991-),男,陕西渭南人,主要从事导弹制导控制方向的研究。
1671-4598(2017)11-0091-05
10.16526/j.cnki.11-4762/tp.2017.11.024
TP3
A
