基于隐马尔科夫模型和支持向量机的模拟电路早期故障诊断
2017-12-15,
,
(北京航空航天大学 可靠性与系统工程学院,北京 100109)
基于隐马尔科夫模型和支持向量机的模拟电路早期故障诊断
郑志文,王晓峰
(北京航空航天大学可靠性与系统工程学院,北京100109)
针对模拟电路在故障预测与健康管理(PHM)系统中早期故障识别率不高的问题,提出了一种基于隐马尔科夫模型(HMM)和支持向量机(SVM)相结合的模拟电路故障诊断方法,利用HMM对动态连续信号的较强识别能力和SVM良好的模式分类能力解决模拟电路早期故障诊断问题;采用主成分分析(PCA)和K-means聚类算法对故障数据进行数据降维和特征提取,建立HMM与SVM相结合的诊断模型进行故障诊断;仿真实验表明,HMM-SVM能很好地识别模拟电路早期故障,并对模拟电路中元件小范围参数变化的状态识别,相较单一HMM模型具有更高的准确率。
隐马尔科夫模型;支持向量机;故障诊断;模拟电路;早期故障
0 引言
在电子系统中,模拟电路的故障数占故障总数的80%,由于存在故障模型复杂,元器件参数分散性较大,同时系统非线性等问题,对模拟电路的故障诊断一直都是现代电路研究的热点[1]。模拟电路的故障可分为硬故障和软故障两种,硬故障是指电路中的元器件参数发生“质”的变化,从而导致系统严重失效,如断路、短路、元器件损坏等。软故障通常是指元器件参数在受到时间和环境的影响下,逐渐偏移出其容差范围,从而导致系统出现功能性故障或性能的恶化。目前,对硬故障诊断的研究已经取得较好的成果,而对软故障诊断尤其是早期故障诊断依然有很多尚待解决的问题。
为了降低由模拟电路故障而导致的系统故障所造成的损失,故障预测与健康管理(PHM)在电子系统中的实际应用已成为未来的发展趋势。PHM指的是使用先进的传感器对系统的各项状态参数进行实时的监测和收集,通过建立智能算法和模型对收集的参数进行系统状态的评估,并提供系统故障的预测,为系统的维修保障提供合理的决策,以实现系统的状态维修[2]。PHM技术的主要目的在于在系统故障发生之前对系统进行状态监测,对于模拟电路的软故障,目前大多数文献将故障元器件的参数偏离其正常值的50%以上定义为软故障,而对参数大于容差范围但小于标称值50%之间的元件,此时元件还未故障,电子系统未完全失效,若此时能够对元件的状态进行一个准确地判断,在软故障发生之前替换故障元件,能够起到防范于未然的作用,对电子系统是一个很好的保护。然而,在该参数范围内的元件,变化范围越小,输出的特征与正常状态相比对越不明显。现常用的模拟电路诊断方法是对在电路发生硬故障或元件参数偏离较大情况下的软故障有较好的诊断识别效果,而对于在元件参数偏离较小的情况下效果不是很理想。因此,本文将大于元件容差小于软故障判定参数之间范围分为2类,分别定义为早期故障和中期故障,加上软故障状态和容差范围内的正常状态共4种状态,如表1所示。
隐马尔可夫模型(Hidden Markov Model,HMM)是一种最初由马尔可夫链发展而来的统计概率模型,可以描述含有一个隐含参数的马尔科夫过程[4],由Baum和Peterie在1966年提出, 70年代HMM被应用在语音识别领域并取得良好效果,80年代中期逐渐应用到模式识别、信号处理等领域[5]。作为信号动态时间序列的统计模型,HMM可以通过严格的数据结构和可靠的模型对时间范围的统计信息进行建模。由于模拟电路的软故障具有动态变化的特点,相比一些停留在静态分析的传统故障诊断方法,能够更好地保留样本数据的统计信息,具有更高的识别率[7]。
支持向量机(support vector machine,SVM)是一种集成了最大间隔超平面、凸二次规划、Mercer核、松弛变量和稀疏解等技术,能够较好地实现了结构风险最小化思想并且具有较好学习能力的通用学习机器。对于小样本、高维数、非线性等问题,它都能够很好地解决并具有良好的泛化能力。对于非线性问题,它提出通过核函数将低维的样本空间变换到高维空间,以较大的距离将样本类别分开,具有很好的分类能力[8]。
HMM适合处理动态连续变化,能够很好地表示类别内的相似性,但在确定最相似模型比较输出概率时,有可能出现多个HMM模型的最大似然概率过于相近或相等,存在误判的风险。因此本文引入SVM与HMM组成HMM-SVM模型,利用SVM适合于处理分类,能够最大程度反映出类别间差异的优势,对模拟电路的参数变化情况进行监控,来解决模拟电路软故障及早期故障诊断准确率不高的问题。
1 HMM-SVM故障诊断模型
1.1 HMM基本原理
HMM作为一种用于描述随机过程统计特性的概率模型,主要由两个随机过程组成,其中一个用来描述每个实际状态之间的转移概率分布,另一个用来描述每个状态在其观测序列的概率分布。模型中实际状态是不可观测,隐藏的,只有通过观测序列获得状态序列的描述,因此称为HMM[4]。
一个HMM可以通过以下参数描述:
1)N:模型中马尔科夫链的状态数目。记N个状态为S1,S2,…,Sn,记t时刻马尔科夫链所处的状态为q,且q∈{S1,S2,…,Sn}。
2)M:每个状态对应的可能观测数目,记M个观测值为o1,o2,…,om,记t时刻的观测值为oi,且oi∈{o1,o2,…,om}。
3)π:初始概率分布,π=(π1,π2,…,πN),其中:
πi=P(qi=Si),1≤i≤N
(1)
qi表示初始时刻的状态。
4)A:状态转移概率矩阵,A={αij}N×N,其中:
αij=P(qi+1=SJ|qi=Si),1≤i,j≤N
(2)
5)B:观测值概率矩阵,B={bjk}N×M,其中:
bjk=P(oi=Vk|qi=Si)
1≤j≤N,1≤k≤M
(3)
对于连续HMM,B是一组观察值概率函数,即B={bj(X),j=1,…,N}。
因此,可以将一个HMM记做:λ=(N,M,π,A,B),简写为:
λ=(π,A,B)
(4)
HMM主要解决评估问题、解码问题和学习问题[14]。评估问题主要解决对于给定一个观测序列,该观测序列是由已确定的HMM产生的概率大小问题,即已知给定模型λ和观测序列O,计算概率P(O|λ),通常由前向-后向算法解决;解码问题是解决对于给定一个观测序列和确定的HMM,通过两者确定HMM内的隐含状态序列的问题,即给定模型λ和观测序列O,求可能性最大的状态序列Q,通常是由Viterbi算法实现;学习问题是解决如何根据给定的观测序列和其相对应的状态序列,在最大似然意义上学习得到一个合适的HMM问题,即模型的训练问题,对给定观测序列O和其相对应的状态序列Q,学习得到模型λ=(π,A,B),使得P(O|λ)最大,通常由Baum-Welch算法训练[9]。在模拟电路的故障诊断问题中,主要是解决学习和评估问题,即先建立合适的模型再通过已建立的模型进行系统状态的识别。
1.2 SVM基本原理
SVM是一种在统计学习的理论框架下,采用结构风险最小化准则的学习机器。它是通过最大化分类间隔以最小化VC维(函数集的复杂度),在保证经验风险(训练误差)的基础上最小化置信风险,使得实际风险达到最小,从而获得更好的推广能力[10]。
给定训练样本集D={(x1,y1),(x2,y2)...,(xm,ym)},yi∈{-1,+1},其中yi为类别函数,xi可能是对象样本中的某些特征值直接构造的向量,也可能是通过某个核函数将原始向量映射到高维空间的映射向量。
在样本空间中构造超平面(即分割平面):
ωTx+b=0
(5)
其中:ω=(ω1;ω2;...;ωd)为法向量,决定了超平面的方向;b为位移项,决定了分割平面与原点之间的距离。
假设超平面(ω,b)能将训练样本正确分类,即对于(xi,yi)∈D,若yi=+1,则ωTxi+b>0;若yi=-1,则ωTxi+b<0。令:
(6)
ω可以描述为:
i=1,2,...,1
(7)
定义判别函数:
f(x)=ωTx+b
则测试集的分类函数可以描述为:
label(x)=sign(f(x))=sign(ωTx+b)
(8)
可以通过求公式的最小值来获得最大的分类边界,即:
(9)
满足的约束条件:
yi(ωTxi+b)≥1-δi,i=1,2,...,n
δi≥0,i=1,2,...,n
(10)
求解上述函数的解可等同于求下面函数的最大值,即:
(11)
并且满足约束条件:
0≤αi≤c,i=1,2,...,n
式中,k(xiyj)是核函数,最后求得分类函数为:

(12)
通过训练数据获得最优超平面后,对于给定的未知样本,只需要代入式子12计算获得指示函数的值,通过该值便可判断样本所属的分类。
1.3 基于HMM-SVM的混合诊断模型
HMM可以根据模拟信号的时序关系对模拟电路的响应进行建模,并且可以反映信号的变化趋势,但只能通过最大似然概率判断类别,如果出现相同最小概率,容易出现误判;SVM的故障诊断则是依据当前时刻的信号特征进行诊断,不考虑前后时刻响应信号之间的联系与影响,具有较好的分类能力,因此,HMM与SVM两者的结合能够较好地克服各自的不足。
基于HMM-SVM模型的模拟电路故障诊断的具体流程如图1所示。
1)首先对训练样本数据进行数据预处理和特征提取。利用主成分分析方法对原始特征向量进行降维处理,并采用k-means聚类算法生成训练HMM模型所需要的状态观测序列O;
2)利用Baum-Welch对HMM模型进行训练,排除似然概率小的类(通过试验表明去除总类数的一半时HMM-SVM的诊断表现最佳)。
3)将剩余的类作为候选模式集,候选模式集中每类故障模式中的特征向量与故障模式标签进行组合送入SVM分类器中进行训练。
4)诊断时,对测试样本数据做与训练样本同样的预处理和特征提取后,输入到训练好的HMM,计算与各状态HMM模型的最大似然概率,即匹配程度,排除较小的类,再利用训练好的SVM对剩余的类进行状态识别,从而获得诊断结果。
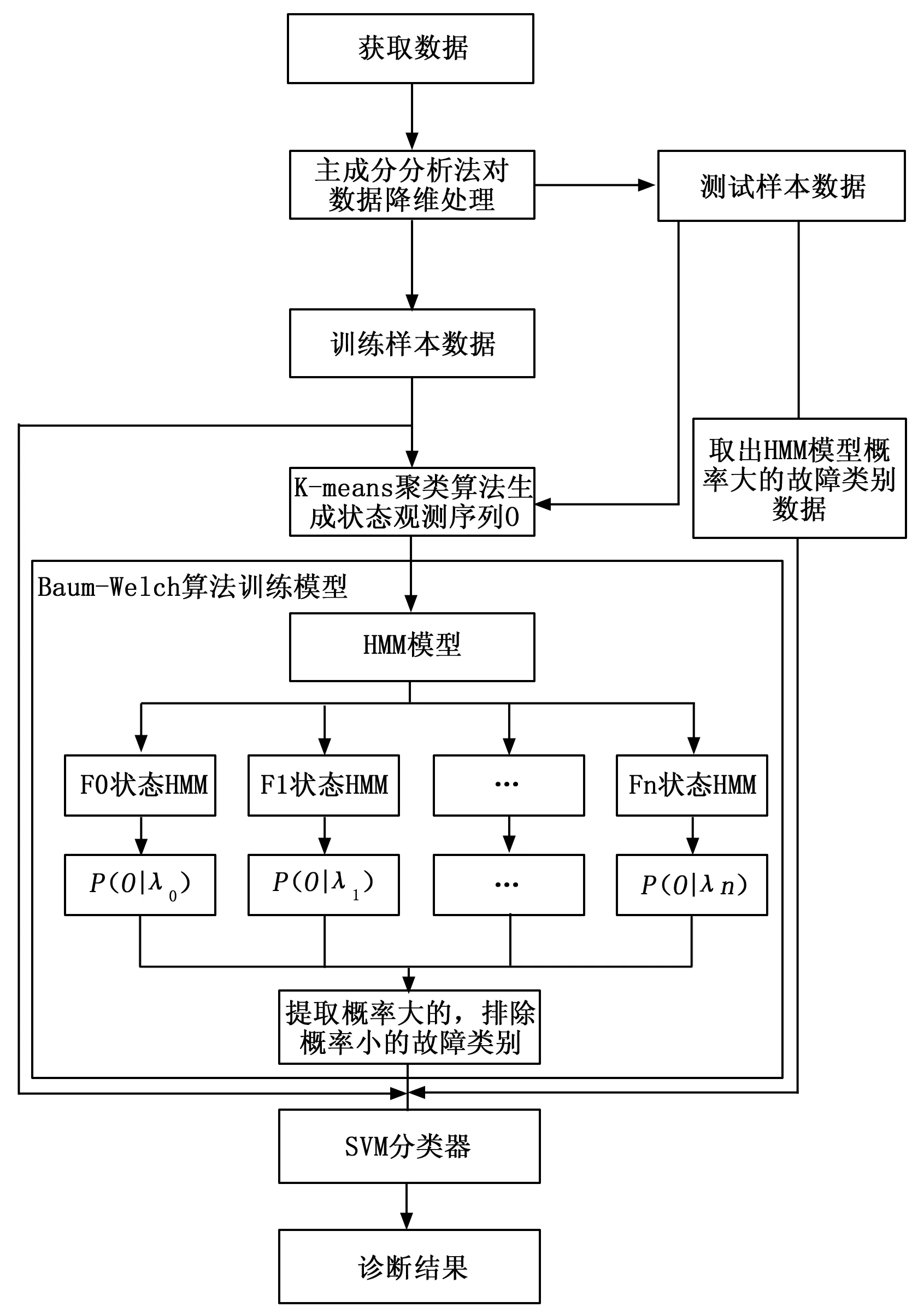
图1 基于HMM-SVM故障诊断流程图
2 基于HMM-SVM的模拟电路故障诊断
二次高通滤波器[11]如图2所示,其中R1=R2=R3=6.2 kΩ,R4=R7=R8=R9=R10=1 kΩ,R5=R6=5.1 kΩ,C1=C2=5 nF,设置电阻电容的容差范围分别为标称值的±5%和±10%。通过对电路进行灵敏度分析得到C1,C2,R1,R7的参数变化相较其它元件对电路的输出变化影响较大,如图3为C1,C2,R1,R7在早期故障模式下与正常状态的输出响应对比曲线,故障模式下的响应曲线与正常状态下的响应曲线差异明显,因此将C1,C2,R1,R7设置为故障元器件。为了更好地识别电路的早期故障,将元器件状态分为正常状态、早期故障、中期故障和完全故障,各状态对应的元器件参数变化如表1所示。因此可将该电路故障类型分为13种,分别为正常状态,C1早期故障,C1中期故障,C1完全故障,C2早期故障,C2中期故障,C2完全故障,R1早期故障,R1中期故障,R2完全故障,R7早期故障,R7中期故障,R7完全故障,相对应的故障编号分别为F0~F12。
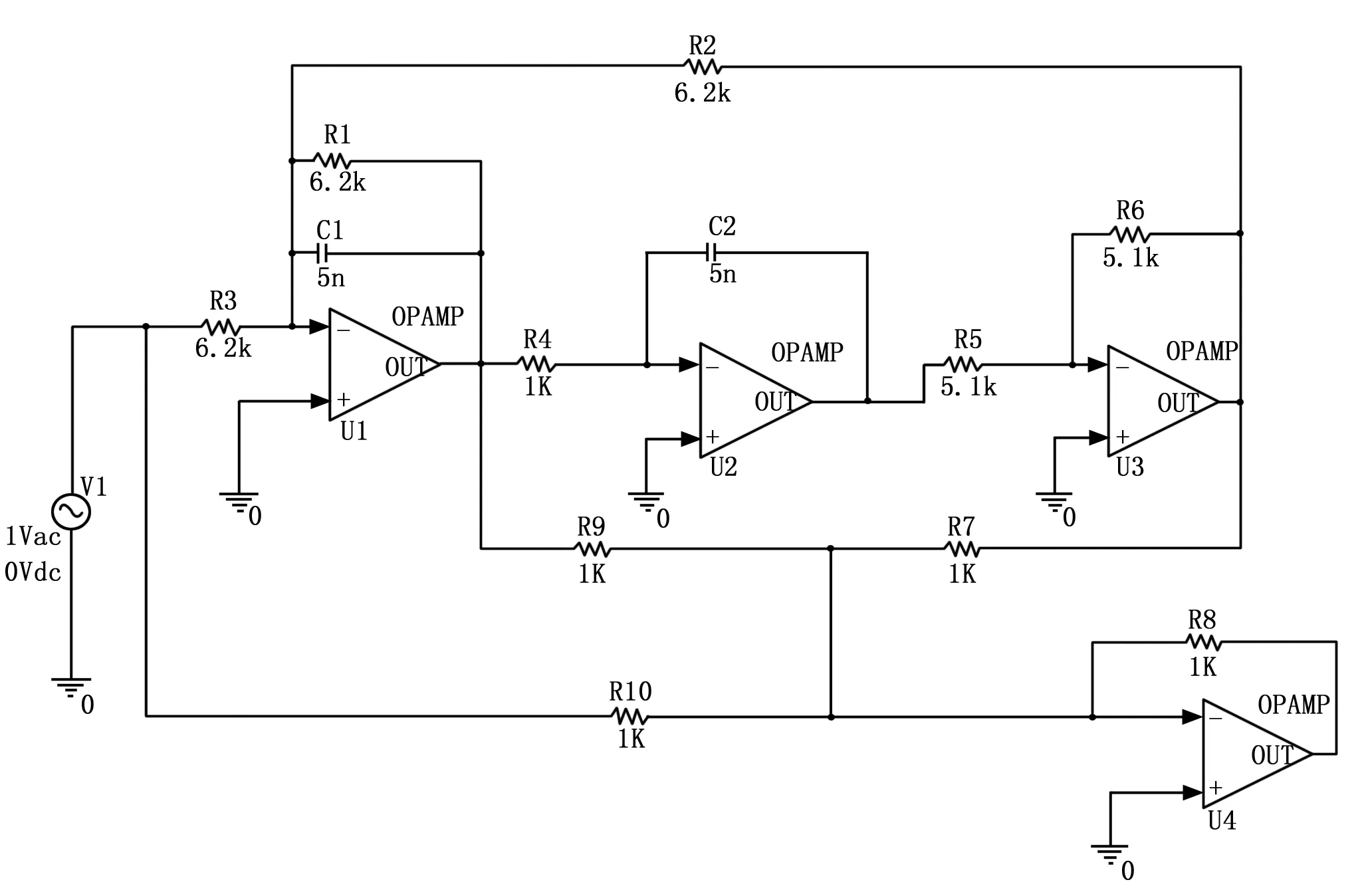
图2 四运放双二次高通滤波器

图3 C1,C2,R1,R7的各自故障与正常情况下的输出响应曲线
电路激励源的电压设置为1 Vac,幅角为0°,电路输出点作为测试点,使用Pspice软件对电路进行13种状态的模拟仿真,每种状态下进行50次蒙特卡洛分析,仿真时任意时刻只有一个元件的参数值在其故障范围内变化,其它剩余元件均在容差范围内变化,正常态时所有元件都在容差范围内变化。在1 kHz到100 kHz提取输出电压值,采样点数为50个,每种状态都对应形成50个50维的特征向量。其中每种状态的1~35为训练样本,后15个作为测试样本。
故障诊断的过程主要包括数据处理与特征提取,模型的建立与训练,故障识别等步骤。如图4所示。

图4 基于HMM-SVM的诊断流程图
2.1 数据处理与特征提取
样本数据的高维度容易对模型诊断的准确率造成影响,本文采用主成分分析(PCA)[12-13]方法对样本数据进行降维处理。PCA是一种对数据信息进行处理、压缩和抽取的常用方法,主要用于高维数据的降维,其方法主要是通过某种线性投影,将数据从原始高维空间映射到低维向量空间,并且使得数据在低维空间的方差最大,维数降低后的向量依然可以保留原始数据的主要信息。
对上面故障特征值构成的原始样本集(Xij)m×n(m为样本数目,n为故障特征值的数目),特征提取的步骤为:
①确定系统的参考数列和比较数列。反映系统行为特征的数据序列,称为参考数列。由影响系统因素组成的数据序列,称为比较数列。
1)原始数据标准化:
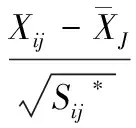
j=1,2,...,n
(12)
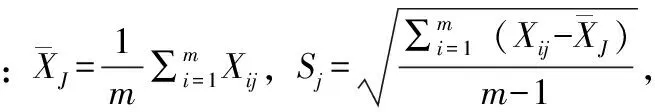
2)建立样本数据的协方差矩阵,并求出其特征值与特征向量:
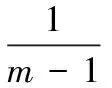
(13)
其中:R样本相关矩阵Λ=diag(λ1,λ2,...,λn),λ1≥λ2≥…≥λn。U=[u1,u2,...,un]是与特征值相对应的标准正交特征向量组成的矩阵。
3)计算前k个主元的方差贡献率ηk,通过方差贡献率大小选取主成分:
(14)
ηk反应的是新生成分量对原始数据的保存程度。
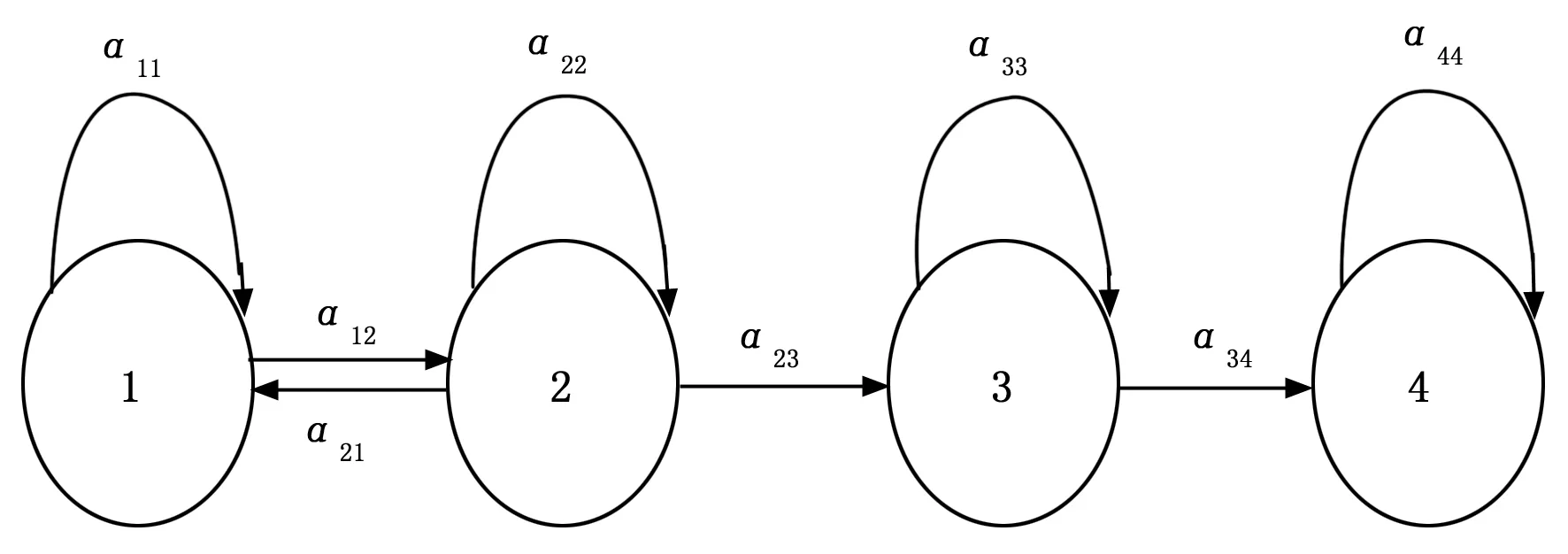
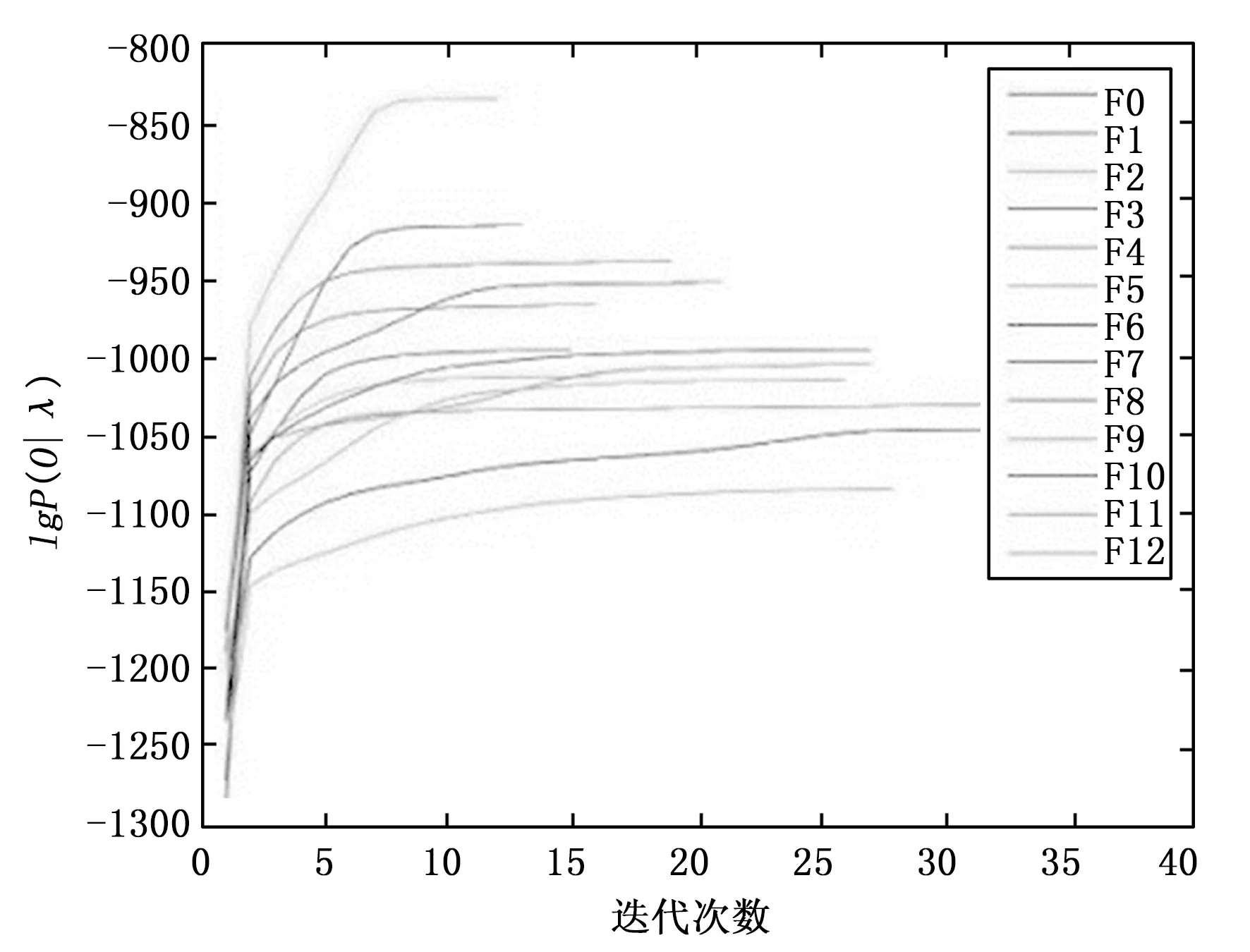
K=[u1,u2,...,uk],k 5)建立故障特征向量。 根据公式T=XK计算出所需的故障特征主成分值。 在本例电路中,根据计算可得当取主元值为13时(即将每类故障状态的特征向量维数由50降为13),方差贡献率达到99%,能够很好的反应原始特征数据集。 2.2.1 HMM模型的建立与训练 由于模拟电路的状态具有连续性和渐变性的特点,因此HMM模型的基础结构应该是左右型模型,同时,模拟电路存在早期故障和完全故障,可定义一个4种状态的HMM模型,各状态分别为正常状态、早期故障、中期故障、完全故障。早期故障状态大多是受到环境的影响而出现的暂时性失效,与正常状态之间的转换是可逆的,而其他状态之间不具有可逆性。HMM模型的初始概率π=[1,0,0,0],HMM模型的结构如图5所示。A=[0.5,0.5,0,0;0.25,0.25,0.5,0;0,0,0.5,0.5;0,0,0,1],观察序列O由样本数据集利用k-means算法聚类得到。由此,可利用Baum-Welch算法训练建立隐马尔科夫模型λ=(π,A,B)。 图5 HMM模型的马尔科夫链示意图 为了提高HMM诊断模型的鲁棒性,采用Baum-Welch算法对多个观察序列进行训练: 1≤i≤N,1≤j≤N 1≤j≤N,1≤k≤M (15) 其中:α为前向变量,β为后向变量,L为观测值序列的数量。 图6 各类HMM模型训练迭代收敛图 2.2.2 SVM模型的选择与训练 SVM主要用来处理二元分类问题,当需要进行多类别分类时,就需要通过构造合适的多类分类器来解决。目前较常用的方法有:一对一、一对多、有向无环图等。由于“一对一”方法具有单个SVM训练规模较小,训练数据均衡且易于拓展的特点,因此这里选用“一对一”方法。在诊断时,使用投票法计算每种类别得票的多少来进行决策。 常用的SVM核函数有:线性核、高斯核、多项式核、拉普拉斯核等。这里采用的是高斯核函数: (16) 通过对这165个样本向量进行测试诊断,结果见表2所示。 表2 HMM与HMM-SVM诊断结果比较 由表2可见,HMM-SVM模型的故障准确率相对HMM单一模型平均提升了3.82%,诊断的准确率更加平稳。两者对于模拟电路的早期故障都有较好的识别能力,HMM-SVM对于小范围内参数的变化有着相对更佳的诊断效果。总之,HMM-SVM模型相较于单一HMM模型在模拟电路故障诊断有很好的改进,诊断效果良好。 基于HMM-SVM模型对模拟电路的早期软故障诊断有着很好的效果,相比单个HMM模型,能更加准确地识别元件小范围参数的变化所带来的电路状态变化,准确率提升了3.82%。 由于HMM-SVM能很好地识别模拟电路小范围参数变化导致的电路状态变化,该模型非常适用于模拟电路的状态监测,应用在模拟电路的故障预测与健康管理(PHM)能够取得较好的效果,具有良好地应用价值和借鉴意义。 [1] 黄 洁, 何怡刚. 模拟电路故障诊断的发展现状与展望[J]. 微电子学, 2004, 34(1):21-25. [2] 周 林,赵 杰. 装备故障预测与健康管理技术[M]: 北京:国防工业出版社,2013. [3] 李向前. 复杂装备故障预测与健康管理关键技术研究[D]. 北京:北京理工大学, 2014. [4] Baruah P, Chinnam R B. HMMs for diagnostics and prognostics in machining processes[J]. International Journal of Production Research, 2005, 43(6):1275-1293. [5] Freeman L G. The Many Faces of Altamira[J]. Complutum, 1994, 5:331-342. [6] Abramovich Y, Spencer N K, Turley M D E. Time-Varying Autoregressive (TVAR) Models for Multiple Radar Observations[J]. IEEE Transactions on Signal Processing, 2007, 55(4):1298-1311. [7] Tai A H, Ching W K, Chan L Y. Detection of machine failure: Hidden Markov Model approach[J]. Computers & Industrial Engineering, 2009, 57(2):608-619. [8] 薛 毅. 最优化原理与方法[M]. 北京:北京工业大学出版社, 2001. [9] 许丽佳. 电子系统的故障预测与健康管理技术研究[D]. 成都:电子科技大学, 2009. [10] 宋国明. 基于提升小波及SVM优化的模拟电路智能故障诊断方法研究[D]. 成都:电子科技大学, 2010. [11] Aminian F, Aminian M, Collins H W J. Analog fault diagnosis of actual circuits using neural networks[J]. Instrumentation & Measurement IEEE Transactions on, 2002, 51(3):544-550. [12] Guo S, Lin-Shi X, Allard B, et al. Digital Sliding-Mode Controller For High-Frequency DC/DC SMPS[J]. Power Electronics IEEE Transactions on, 2010, 25(5):1120-1123. [13] 陈绍炜, 吴敏华, 赵 帅. 基于PCA和ELM的模拟电路故障诊断[J]. 计算机工程与应用, 2015, 51(11):248-251. [14] Rabiner L R. A tutorial on hidden Markov models and selected applications in speech recognition[J]. Proceedings of the IEEE, 1989, 77(2):267-296. IncipientFaultDiagnosisofAnalogCircuitsBasedonHMM-SVM Zheng Zhiwen,Wang Xiaofeng (Reliability and System Engineering Academy,Beihang University,Beijing 100109,China) Considering the problem that the rate of incipient fault diagnosis of analog circuit is not high in Prognostics and Health Management(PHM), an fault diagnosis method of analog circuit based on HMM and support vector machine (SVM) has been proposed.Using HMM’s strongly identify dynamic continuous signals ability and SVM’s great pattern classification ability to solve incipient fault diagnosis of analog circuits.The principal component analysis (PCA) and K-means clustering algorithm are used to reduce data dimension and extract the fault data, and then establish HMM-SVM model for fault diagnosis.Simulation results show that HMM-SVM can well identify the ncipient fault of analog circuit and identify the state of small-scale parameter variation in the analog circuit, which has higher accuracy than single HMM model. hidden Markov model;support vector machine;fault diagnosis;analog circuits;incipient fault 2017-04-18; 2017-05-26。 郑志文(1993-),男,江西南昌人,硕士研究生,主要从事测试性与故障诊断方向的研究。 王晓峰(1964-),男,黑龙江哈尔滨人,副教授,硕士研究生导师,主要从事故障诊断与测试性方向的研究。 1671-4598(2017)11-0013-05 10.16526/j.cnki.11-4762/tp.2017.11.004 TP3 A2.2 基于HMM-SVM模型的训练


3 基于HMM-SVM的故障识别与结果分析
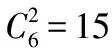

4 结论
