基于激光点云的路桥平面线形拟合方法

邬镇伦*，程效军,2，杨泽鑫，吴飞飞

（1.同济大学 测绘与地理信息学院，上海，200092；2.现代工程测量国家测绘地理信息局重点实验室，上海，200092；3.江西省交通建设工程质量监督管理局，江西南昌，330000）

基于激光点云的路桥平面线形拟合方法

邬镇伦1*，程效军1,2，杨泽鑫1，吴飞飞3

（1.同济大学 测绘与地理信息学院，上海，200092；2.现代工程测量国家测绘地理信息局重点实验室，上海，200092；3.江西省交通建设工程质量监督管理局，江西南昌，330000）

快速、准确的平面线形拟合方法对于路桥养护及其改扩建工程来说至关重要。本文提出一种基于激光点云的路桥平曲线参数拟合方法。该方法基于既有桥梁的三维点云数据，拟合求得分段三次样条函数模型，结合各段函数模型特点计算获取平曲线参数。结合广州市某市政桥梁养护工程进行方法有效性验证，实验结果表明：与传统拟合方法相比，本文方法具有速度快、自动化程度高等优点。

平面线形拟合；三次样条曲线拟合；曲线单元识别；三维激光扫描

引言

条函数模型，结合各段函数模型特点识别各曲线单元并计算获取平曲线参数，算法流程如图1所示。

图1 路桥平面线形拟合流程图

随着我国“7918”公路网的不断完善，交通部对公路信息化建设提出了新的规划和要求。然而，许多既有路桥存在早期建设与管理不够规范、施工过程中产生设计变更以及后期改扩建等现象。这些现象均导致既有路桥的线形资料不全或与实际情况不符，给路桥的养护管理造成了很大困扰。因此，如何运用现有的技术设备快速高效地拟合既有路桥平面线形参数成为了科研人员急需解决的问题。

目前较为成熟的测量方案是利用 GPS获取路桥中线的离散点坐标进行线形拟合,该方法属于传统的单点采集法，存在工作效率低，劳动强度大，离散点密度小且选取易受人为因素影响等缺点。而LiDAR测量系统作为实时获取地形表面三维点云和影像的遥感系统[1]，与传统测量手段相比具有快速性、主动性、高密度、高精度等特点，可以弥补传统方案的缺点。根据这些特点，本文提出一种基于激光点云的路桥平面线形拟合方法，为既有路桥的养护管理提供了参考依据。

1 平面线形拟合方法

本文所提出的路桥平面拟合方法以既有路桥的三维点云作为基础数据提取路桥中线点云，拟合该中线点云求得分段三次样

1.1 路桥中线点云提取

（1）将原始点云投影至水平面XOY上，如图2（a）所示；

（2）沿 X轴方向设置适当的步长△x，求出该步长范围内投影后的点云在 Y轴方向上的最大值和最小值，定义步长范围内的理想中心点为M（x,y），根据公式（1）、（2）求出M点坐标，考虑到理想中心点并非一定存在于原始点云数据，故提取出该步长范围内点云中距离此理想中心点最近的点。

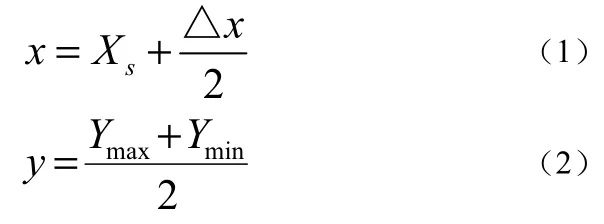
（3）循环执行上述步骤以提取出路桥中线点云。图2（b）为经步长搜索法后提取出的路桥中线点云。

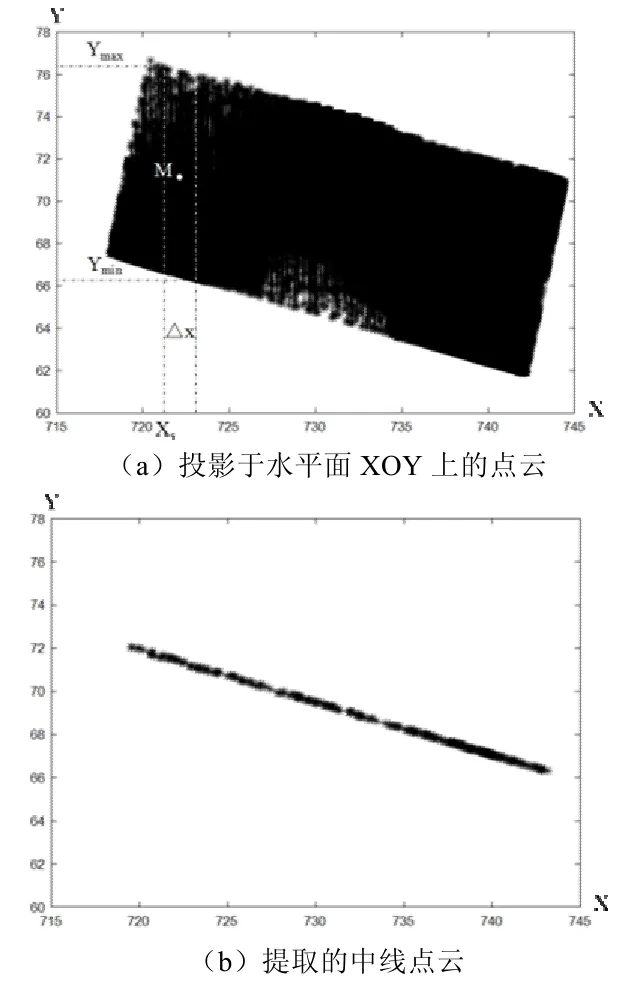
图2 路桥中线点云提取

1.2 三次样条曲线拟合

由于路桥平曲线多采用直线-缓和曲线-圆曲线的组合形式，所以本文在提取路桥中线离散点云后，采用三次样条函数模型对离散点进行分段拟合[2]，计算中线点云上相邻两点之间的多项式表达式以及各点曲线曲率，求得三次样条曲线表达式系数及端点曲率表。

根据三次样条曲线的定义：若函数S(x)∈C2[a,b]（C2[a,b]表示区间[a,b]上具有二阶连续导数的函数的全体），且在每个小区间[xj，xj+1]上是三次多项式，其中a=x0＜x1＜…＜xn=b是给定节点，则称S(x)是节点x0， x1，…，xn上的三次样条函数。若将中线点云坐标X定义为三次样条函数S(x)的节点xn，则对路桥中线平曲线的求解便转化为对三次样条函数S(x)的求解。

关于三次样条函数S(x)的求解过程如下：

定义 S(xi)=yi(i=0，1，…，n)表示这个函数代表曲线上所有各点。设S(x)在节点xi处一阶、二阶导数值分别为mi、Mi，即：

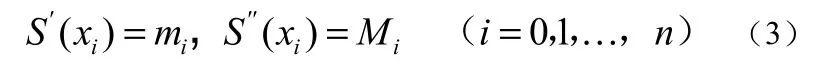
因为S(x)在每个区间[xi，xi+1]（ i=0，1，…，n）上是分段三次多项式，则S''(x)在区间[xi，xi+1]上是线性函数，即：

笔者曾对维和军人进行思维方式相关项目研究，结果提示“模拟式启发”训练能够在消极结果的事件中产生下行反事实思维，改善情绪表现[8]。Kneepkens等[9]对抑郁症住院患者予以心理和抗抑郁药物治疗研究，患者不成熟的防御方式显著降低，成熟的防御方式显著提高，提示防御方式的可变性，这从另外一个方面佐证了情绪对思维、对防御方式的影响。因此，通过有目的地指导防御方式可以改变认知，有利于创造性思维水平的提高。

公式（4）中，hi=xi− xi−1，对式（4）二次积分，得：

对公式（5）进行微分，得：

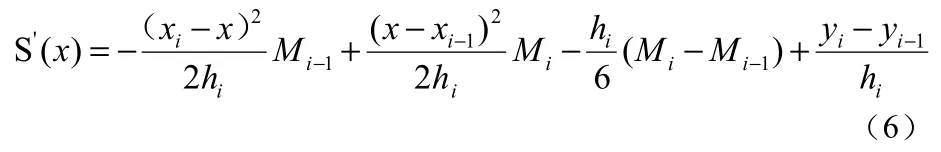
因为曲线在区间端点i处连续，由（6）得：

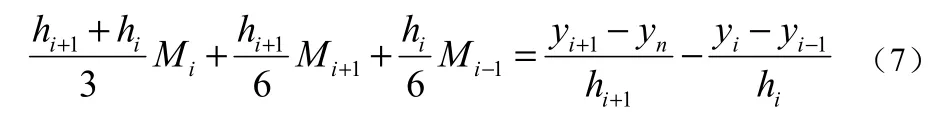
将式（7）进行整理得：

其中：

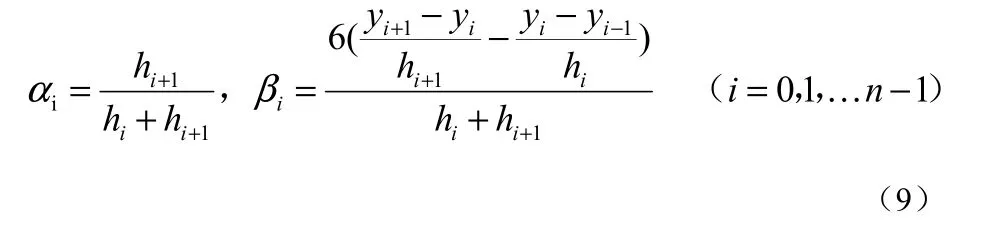
由公式（8）求出参数Mi，再将Mi代入式（5），即可求得分段三次样条函数。通过上述方法可以算得基于三次样条曲线拟合后的中线点云上相邻两点之间的多项式表达式，为后续拾取曲线单元求取平曲线参数提供依据。

1.3 曲线单元识别及求解

路桥中线的平面几何线型由直线和曲线组成，如图3所示。路桥平曲线设计参数主要包括路线偏角，缓和曲线长度ls，圆曲线半径R及曲率参数A等。各参数可按式（10）～（12）进行计算。图4表示各线形单元的曲率变化[3]。

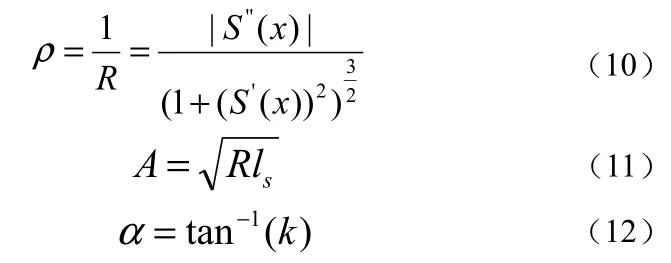
式中 为曲线曲率，k为直线斜率。

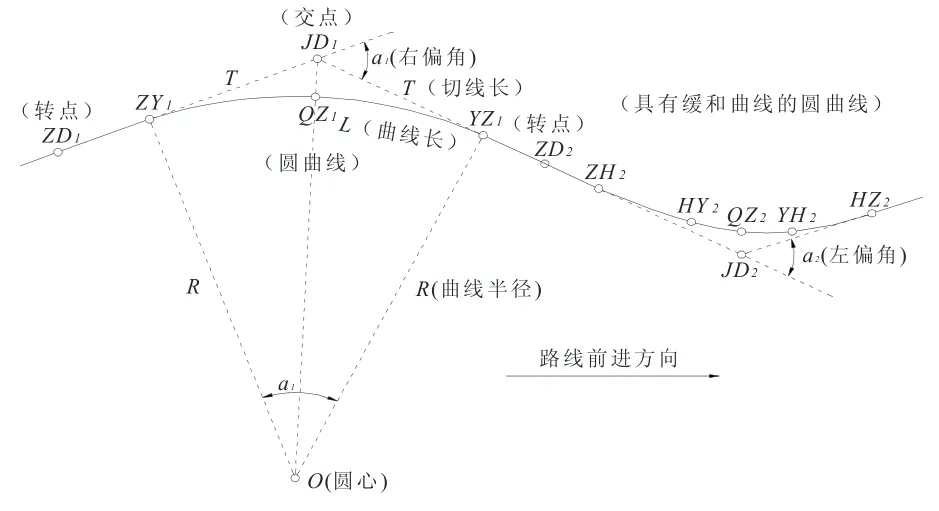
图3 路桥中线

图4 路线曲率

参照《公路工程技术标准》（B01-2014）[4]，曲线半径连续

参照《公路工程技术标准》（B01-2014）[4]，曲线半径连续大于10000m的曲线段即为直线单元，而曲线半径小于10000m且曲率变化率小于某一设定阈值的曲线段即为圆曲线单元，直线与圆曲线之间的连接部分即为缓和曲线单元[5]。

根据上述标准确定直线及圆曲线单元之后，可利用式（10）、（12）计算直线及圆曲线参数（圆曲线半径R可取圆曲线单元各点半径的平均值），而对于缓和曲线参数的求解如果直接利用离散点序来进行求解过程较为繁琐，但在可确定缓和曲线起止坐标的情况下，对缓和曲线参数的求解即可理解为一个逐步趋近的过程，为求得确定的A值，可采用黄金分割优选法[6]，即最小化目标函数达到一定的精度时，A值即为所求。

2 工程实例

2.1 工程概况

广州市某市政桥梁，建于1981年，桥面净宽7m，设计速度为 40km/h，由于早期建设与管理不够规范导致施工图纸丢失。现要求恢复其平面线形，为后期桥梁养护施工提供设计依据。

采用FARO Focus3D X330三维激光扫描仪采集该桥梁的三维点云数据，使用FARO SCENE软件对原始点云进行配准、压缩及去噪等数据预处理，所得该桥的点云点数为 671628，点云效果如图5所示。

图5 某桥梁点云图

2.2 拟合结果与分析

本文基于MATLAB进行算法测试，求得部分三次样条曲线表达式系数及端点曲率如表1所示，平曲线参数拟合结果如表2所示。

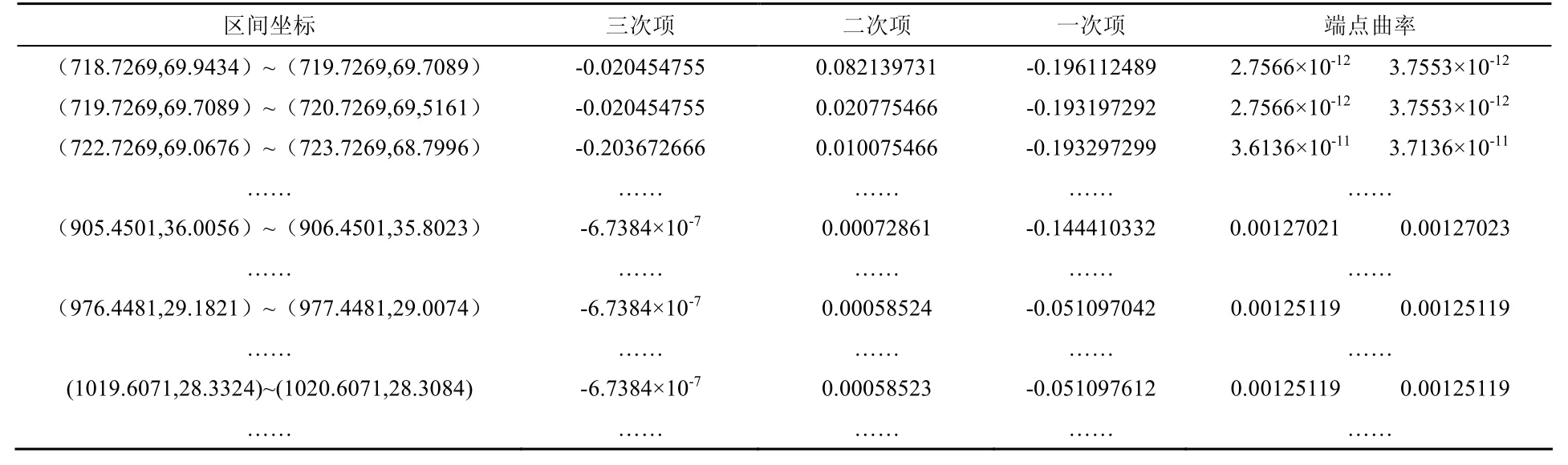
表1 部分分段三次样条曲线表达式系数、端点曲率

表2 平曲线参数拟合结果

从上述拟合结果可以看出，该桥梁平曲线存在一个交点，缓和曲线长ls= 140.516m，圆曲线半径长R = 799.484m，均满足《公路路线设计细则》（JTG/T D20-2014）[7]的要求。

为了检验本文方法的有效性，根据该桥梁所在位置处的1：500的地形图，不考虑存在匝道以及桥面变宽的情况，采用最小二乘法拟合出地形图上桥梁边界线的曲线参数，计算结果与本文方法拟合结果比较如表3所示。

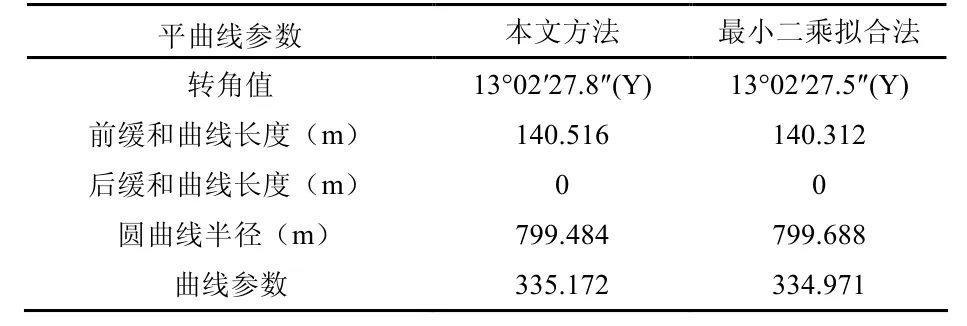
表3 两种方法结果比较

由表3可知，拟合结果在满足设计规范的要求下与最小二乘法拟合出的结果非常接近，这验证了本文方法的准确性及普遍适用性。

3 结束语

本文提出了一种基于激光点云数据的路桥平面参数拟合方法，与传统方法相比，该方法减少了由于数据采集不足所带来的拟合误差，充分利用了LiDAR测量系统速度快、自动化程度高的特点，为路桥改扩建及其养护工程提供了设计依据，有较高的实用价值。但是，本文方法没有考虑路桥存在匝道以及路桥面部分变宽等复杂情况。因此，后续工作将着重于研究如何在该复杂情况下拟合出路桥点云的中线参数。

[1]Baltsavias E P. A comparison between photogrammetry and laser scanning[J]. Isprs Journal of Photogrammetry & Remote Sensing,1999,54(2-3)： 83-94.

[2]张航,张肖磊,张汉龙. 改扩建公路平面线形参数识别原理及其应用[J]. 公路,2017,(1)： 27-31.

[3]顾孝烈,鲍峰,程效军. 测量学,(第五版)[M]. 同济大学出版社,2016.

[4]单位交通部公路司中国工程建设标准化协会公路工程委员会. 公路工程技术标准（B01-2014）[M]. 人民交通出版社,2014.

[5]张志伟,刘志刚,黄晓明,等. 基于LIDAR数据的道路平面线形拟合方法研究[J]. 公路交通科技,2009,26(12)： 17-22.

[6]李方. 公路立交匝道布线作图法[J]. 公路,1992,(5)： 31-34.

[7]交通部第一公路勘察设计院. 公路路线设计规范（JTG/T D20-2014）[M]. 人民交通出版社,2014.

Fitting method of Highway Bridge Horizontal Alignment Based on Point
Cloud Data

WU Zhenlun1*,CHENG Xiaojun1,2,YANG Zexin1,WU Feifei3
(1.College of Surveying and Geo-Informatics,Tongji University,Shanghai,200092,China; 2.Key Laboratory of Advanced Engineering Survey of SBSM,Shanghai,200092,China;3.Jiangxi Province Traffic Construction Engineering Quality Supervision Administration,Jiangxi Nanchang,330000,China)

Accurate and rapid fitting method of horizontal alignment is critical to highway bridge's maintenance and its reconstruction or exten sion project. In this paper,a method to fit its horizontal alignment parameters with LiDAR data is put forward.By using one municipal bridge maintenance project as an example,the piecewise cubic spline function model,fitted and obtained through the three dimensions scan of the bridge,along with the consideration of the characteristics of each segment function model is used to work out the horizontal alignment paramet ers. This method is proved to be feasible,speedy,and with high degree of automation when comparing with traditional fitting method.

Horizontal alignment; identification; parameter fitting; LiDAR

U412

A

1672-9129(2017)06-0142-03

10.19551/j.cnki.issn1672-9129.2017.06.050

邬镇伦,程效军,杨泽鑫,等. 基于激光点云的路桥平面线形拟合方法[J]. 数码设计,2017,6(6)： 142-144.

Cite：WU Zhenlun,CHENG Xiaojun,YANG Zexin,et al. Fitting method of Highway Bridge Horizontal Alignment Based on Point Cloud Data[J]. Peak Data Science,2017,6(6)： 142-144.

2017-02-12；

2017-03-18。

邬镇伦(1995 -），男，江西宜春人，硕士研究生，研究方向：摄影测量与遥感。

Email：kdzp001@163.com