基于FPGA 的浮点LMS 自适应滤波算法的设计与实现

齐志强*

（中国空空导弹研究院，河南洛阳，471009）

基于FPGA 的浮点LMS 自适应滤波算法的设计与实现

齐志强*

（中国空空导弹研究院，河南洛阳，471009）

针对定点LMS(最小均方误差）自适应滤波算法动态范围小，运算精度差的弊端，提出了一种基于FPGA的浮点LMS自适应滤波算法的实现方法。该方法能够有效降低量化误差造成的性能损失，避免了采用DSP实现算法造成的硬件开销，降低了系统设计复杂度，提高了系统可靠性，同时还具有可移植性强，应用灵活等优点。

自适应；抗干扰；浮点；最小均方误差；FPGA

引言

自适应滤波器是统计信号处理的一个重要组成部分，其性能通常远优于常规方法设计的固定滤波器，因此被广泛应用于通信、雷达、控制、声呐、地震和生物医学等领域[1-2]。最小均方（LMS)自适应滤波算法因其设计简单，性能高效，鲁棒性强而得以广泛应用[3-5]。传统的自适应滤波算法大多基于DSP芯片实现，但存在抗干扰性能差和实时性差的问题[6-7]。随着 FPGA集成度的不断提高，LMS自适应滤波算法逐渐采用FPGA实现，通常采用定点数作为运算的数据格式。但定点运算方式在进行整型化时会引入误差，导致精度下降[8]，并且动态范围较小，难以满足一些对系统性能要求高或对动态范围要求大的应用。对系统性能要求高或对动态范围要求大的应用一般采用FPGA+DSP的硬件架构，系统电路设计复杂，可靠性差。

虽然浮点运算用 FPGA实现占用资源较多，但随着大规模FPGA的普及，资源问题已不再成为问题的瓶颈[9]。本文提出了一种基于FPGA的浮点LMS自适应滤波算法的设计与实现方法，在硬件上去掉了 DSP芯片及其外围电路，电路大大简化，电路面积可减少约40%。由于不再需要FPGA与DSP间通过大量总线进行信息交互，提高了系统的可靠性，在不失灵活性的前提下提升了运算的性能[10]，适用于对性能要求较高的应用场合。

1 LMS自适应滤波算法

LMS自适应滤波算法是一种基于梯度的算法，假定有一个构建好的二次性能表面，当性能表面是天线阵权值的二次函数时，性能表面呈椭圆形的抛物面形状，其中有一个最小值。利用梯度法求最小值，通过求均方误差可构建代价函数。本文以4通道输入信号为例，其中一路作为期望信号，其它三路加权后与期望信号做差，使输出最小即可达到消除干扰的目的[11]，如图所示。

图1 LMS自适应滤波系统

误差为[12]：

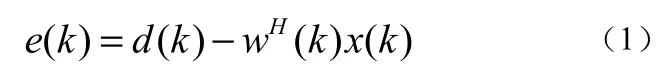
其平方误差为：

去掉与时间相关的符号，则代价函数为：

采用梯度法可求式（3）的最小值，(3)式的梯度

当梯度为零时，权值是最优维纳解，用下式表示：

式（5）是按照知道所有信号的统计数据并计算出相关矩阵为基础的，事实上我们不可能知道这些统计数据，而只能用瞬时估计值来代替，瞬时估计值为：

采用最陡下降法的迭代技术可近似求出代价函数的梯度，最陡下降方向为梯度向量的反方向。最陡下降法可用Widrow所提出的最小均方算法的权值来近似，最陡下降迭代近似由下式给出[13]：

其中，是步长，∇w是性能表面的梯度。

将式（4）代入式（8）中，得[14-15]：

其中e(k)=d(k)− wH(k) x(k)表示误差信号，在本系统中作为消除干扰后的信号输出。当迭代次数趋于无穷时，滤波器的权系数逼近维纳解。式（9）中LMS算法的收敛性与步长 成正比。如果步长太小，则收敛速度缓慢，甚至出现过阻尼情况；如果步长太大，则收敛不到最优权值，权值在最优权值附近振荡[16]。研究表明，要想使算法稳定，需满足[17-18]：

其中λmax为相关矩阵R的最大特征值。由上述分析可知，算法的核心是求出各路权值，权值由式（9）经多次迭代求得，步长因子 由仿真确定。该算法基于浮点运算，故无需仿真确定各级信号位宽。由于LMS算法是一种迭代运算，无法一个时钟输出一次权值，所以计算权值时需要对输入信号进行抽取。为了提高数据有效率，输出数据并不抽取，只需一段数据对应同一组权值即可，即采用分块计算的LMS算法。

2 LMS自适应滤波算法的FPGA实现

浮点运算包括单精度运算和双精度运算，考虑到运算需求和资源消耗等因素，我们采用单精度运算，FPGA选用Altera公司的Cyclone V系列5CEFA9实现。浮点LMS自适应滤波算法的FPGA实现大体分三个步骤：第一步是将输入的定点数据转换为浮点数；第二步是进行浮点LMS运算；第三步是将输出的浮点数转换为定点数。浮点LMS自适应滤波算法顶层模块视图如图2所示：

图2 浮点LMS自适应滤波算法顶层模块视图

定点数转浮点数和浮点数转定点数可以调用Quartus中的免费IP核ALTFP_CONVERT来实现，如图3所示，通过配置IP核ALTFP_CONVERT中的参数，即可实现定点数转浮点数和浮点数转定点数。

图3 ALTFP_CONVERT IP核

从LMS算法的描述可以看出，实现LMS算法只需要完成式（11）和式（12）两个算式的计算。

上面两个算式均为浮点复数运算，只包含加法、减法和乘法三种运算，三种运算均可以调用Quartus中的免费IP核来实现。浮点加法和减法均可以通过调用Quartus中的ALTFP_ADD_SUB IP核来实现，如图4所示。通过配置不同的选项即可实现浮点加法和浮点减法。

图4 ALTFP_ADD_SUB IP核

浮点乘法可以通过调用Quartus中的ALTFP_MULT IP核来实现，如图5所示。

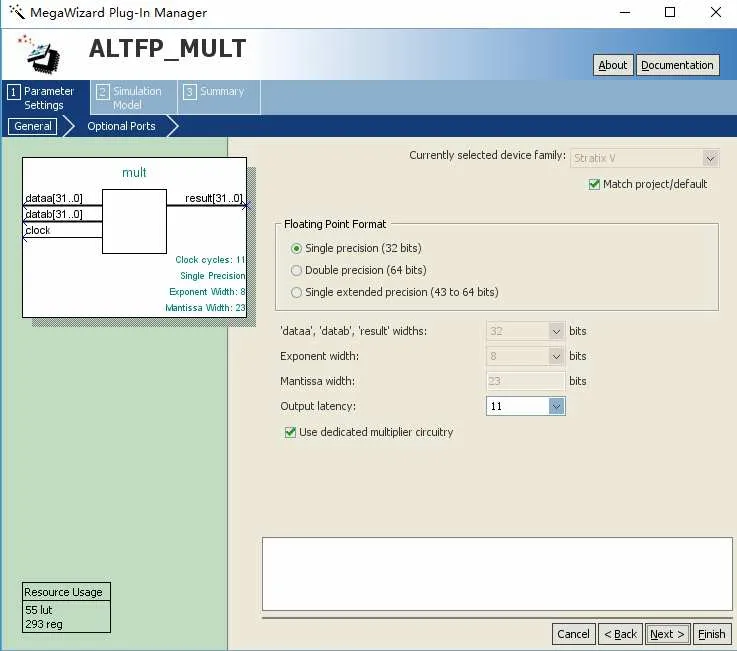
图5 ALTFP_MULT IP核

Quartus中的浮点加法，减法和乘法IP核均可根据需要选择单精度或双精度类型，其输出延迟几个时钟，面积优先还是速度优先等参数均可以根据需要进行配置，根据不同的配置方案，其消耗的资源也各不相同，消耗资源情况可以在配置框图中看到。

算式（11）为LMS算法的输出结果，采用流水线处理方式，可实现每个时钟节拍输出一个数据；算式（12）为权值更新算式，由于e(k)的输出无法用1个时钟周期完成，所以权值的更新需要多个时钟周期。用 1个控制模块来产生各运算模块的控制信号，以实现内部各运算模块的运算控制，保证各模块之间数据衔接稳定、正确，以有效地控制模块的计算，得到准确的计算结果。通过模块化的IP 核配置，并配以简单的时序控制，就可以方便的实现算法。

浮点LMS自适应滤波算法的资源消耗情况如图6所示。

图6 浮点LMS自适应滤波算法的资源消耗情况

从综合仿真结果来看，实现4路浮点LMS自适应滤波算法占用FPGA逻辑资源11%，占用乘法器资源7%，占用存储器资源2%。所选FPGA仅为Altera公司的低端型号，实现4路浮点LMS自适应滤波算法占用资源比例不高，因此该方案具有很强的实用性。

3 结束语

本文所述的基于FPGA的浮点LMS自适应滤波算法，在不降低自适应算法性能，不增加系统功耗和成本的前提下，将原来用DSP实现的浮点运算用FPGA实现，大大减小了电路板面积，简化了电路设计，降低了系统设计复杂度，提高了系统的可靠性。同时该算法可以封装成IP核，可以方便的移植到Altera公司的各系列FPGA中，在后续设计中直接调用，不用再重新编写和调试，缩短了产品开发时间。该方法已在工程上实现，其性能稳定，效果良好，该方法不但可以应用于空域抗干扰算法，也适用于空时抗干扰算法，应用前景广泛。

[1]齐志强. 全球定位系统的抗干扰技术研究[J]. 电子设计工程,2011,19(19)： 112-115.

[2]齐志强. 自适应波束形成技术在 GNSS抗干扰中的应用[J]. 电光与控制,2014,21(10)： 110-113.

[3]赫金著. 自适应滤波器原理(第 5版)[M]. 北京. 电子工业出版社,2016,5.

[4]李鹏程,等. 基于 PI算法的自适应调零天线抗干扰技术研究[J]. 电子科学技术,2016,3(4)： 471-474.

[5]初明阳. 自适应调零天线卫星定位抗干扰算法仿真研究[J]. 航空兵器,2014,(3)： 44-47.

[6]陈亮,等. LMS自适应算法的FPGA设计与实现[J]. 微计算机信息,2012,(7)： 22-23+29.

[7]董祥雷,袁上策,王玲. 一种改进LMS算法的高速FPGA实现[J]. 电子信息对抗技术,2015,(3)： 72-75.

[8]程龙,等. 基于FPGA的浮点FIR滤波器设计[J]. 电测与仪表,2015,(18)： 80-84.

[9]王强. 快速浮点运算在FPGA中的实现[J]. 铜仁学院学报,2014,(4)：104-106.

[10]许鹏,等. 基于FPGA的高性能浮点型FFT处理器设计[J]. 武汉大学学报(工学版). 2015,48(1)： 120-124.

[11]何永前,李建璜. GPS抗干扰接收机自适应天线阵功率倒置算法研究[J]. 舰船电子工程,2012,32(6)： 61-62.

[12]杨帆. 基于 LMS算法的天线波束方向图仿真研究[J]. 现代导航,2013,(6)： 430-433.

[13]聂晓鸿,等. 基于LMS的自适应数字波束形成的FPGA实现[J]. 南京信息工程大学学报,2013,5(3)： 267-272.

[14]繆贲术,严接班,董蛟. 改进步长 LMS算法及其在卫星信号处理中的应用[J]. 舰船电子工程,2016,36(9)： 39-41.

[15]解玲娜,战勇杰,宋振宇. 基于改进 LMS自适应并行多址干扰消除[J]. 电子设计工程,2012,20(9)： 19-22.

[16]田玉坤,等. 功率倒置自适应抗干扰算法的性能分析与仿真[J]. 电子信息对抗技术,2016,31(5)： 66-70.

[17]张红梅,韩万刚. 一种新的变步长LMS自适应滤波算法研究及应用[J]. 仪器仪表学报,2015,36(8)： 1822-1830.

[18]杨文革,等. LMS自适应滤波算法改进及其在连线干涉测量中的应用[J]. 遥测遥控,2016,37(5)： 49-57.

Design and Implementation of LMS Adaptive Filtering Algorithm Based on FPGA

QI Zhiqiang*
（China Air to Air Missile Academy,Henan Luoyang,471009,China)

In view of the lower dynamic performance and bad accuracy operation of LMS adaptive filtering algorithm using fix-point,a design scheme of realize a LMS adaptive filtering algorithm using floating-point based on FPGA was introduced. It is successful to reduce the loss of the performance caused by quantization error,meanwhile,the additional hardware cost is avoid if using DSP to realize. This design method has not only reduce the complexity and enhance the reliability of the system,but also has powerful portability and great flexible application.

Adaptive; Anti-jam; Floating-point; LMS(Least-Mean-Square); FPGA

TN973.3

A

1672-9129(2017)06-0075-03

10.19551/j.cnki.issn1672-9129.2017.06.026

齐志强. 基于FPGA的浮点LMS自适应滤波算法的设计与实现[J]. 数码设计,2017,6(6)： 75-77.

Cite：QI Zhiqiang. Design and Implementation of LMS Adaptive Filtering Algorithm Based on FPGA[J]. Peak Data Science,2017,6(6)： 75-77.

2017-01-23；

2017-03-07。

齐志强（1982-），男，河南南阳人，硕士，高级工程师。研究方向：研究方向为卫星定位及抗干扰技术。

Email：kdzp001@163.com