基于小波神经网络短时交通流量预测

任晓霞*，宋海明

（1.山西工商学院，山西临汾，030003；2.国家电网新疆电力公司经济和技术研究所，新疆乌鲁木齐，830011）

基于小波神经网络短时交通流量预测

任晓霞1*，宋海明2

（1.山西工商学院，山西临汾，030003；2.国家电网新疆电力公司经济和技术研究所，新疆乌鲁木齐，830011）

作为一种人工智能算法，BP神经网络对数据有良好的自学习能力，可以对非线性数据良好逼近，由于其采取的是梯度下降法，容易使搜索陷入局部最小，为了进一步提高预测精度，利用小波良好的时频性，降低网络结构对数据敏感的特点，从而达到良好的预测效果。通过小波分解与重构获取交通流量数据中的低频近似部分和高频随机部分，然后在分析各种模型的优、劣的基础上,选取较有效的模型或模型结合方式,建立了交通流量预测模型。最后，利用实测交通流量数据对模型仿真，结果表明该模型可以有效地提高短时交通流量预测的精度。

短时交通流预测；小波神经网络；BP神经网络

引言

由于我国的经济飞速发展，生活水平不断提高，人们拥有的汽车数量持续增加。目前我国的道路增长速度却无法满足汽车增长速率，这势必造成严重的交通拥堵问题。这种现象的本质就是交通资源和人们的需求不平衡的一种表现。交通系统是一个复杂的系统，有很多的不确定性，和不稳定性，所以迫切需要有效的科学理论来分析，解决这些问题。作为解决交通问题的有效方案，智能交通管理系统，目前被我国广泛应用，智能交通系统一般通过对未来短时间交通流量的精确预测来实时调节道路中的流量分配。历史数据选择一般要求时间间隔很小，通过预测模型的分析，滚动预测未来短时间的交通流量，以便人们外出做好规划行程，使人们避开交通高峰期。同时，交通流量短时预测还可以方便交通部门管理，减少交通事故发生，平衡车流，改善交通运输条件，利于社会和谐。

1 小波神经网络概述

小波变换（Wavelet Transform,WT）是一种新的变换分析方法，它不仅拥有傅里叶变换的特点，而且还使其局部化思想得到进一步发展。由于傅里叶变换理论中频率改变，窗口大小不变。小波变换与傅里叶变换相比有很大不同，频率和窗口大小都是可以相应地改变，利用伸缩因子，平移因子多尺度分解信号，将信号在时域和频域进行详细的分解，对一些微小的问题，进行局部化解决。

2 小波神经网络模型建立

建立城市交通路网络模型，首先确定几个影响交通流量的元素，一般网络模型可以分为3层，即输入数据层，中间层，输出数据层。一般模型结构如图1所示：

图1 寐波神经网络算法结构模型Figure 1 structure model of wavelet neural network algorithm

2.1 相关参数选取

（1）输入节点数

节点数的多少影响训练的精度，节点数过多又影响速度，因此要适当选取节点数，由于交通的实时性决定了本文采用的神经网络是动态的，而且也具有无反馈型的特性。因为输入的是前几个时间点的交通流量数值，因此输出的预测与相近的时间点的流量相关，也就是变成了时间序列的预测。

移动平均法主要依靠时间序列数据，时间序列数据的精确与否直接决定了整个系统的精度。按照顺序逐点向前推移求出 N个数的平均数，然后就可以获取移动平均数：

公式中Mt(1)为第t周期的移动平均数；Mt-1(1)为第t周期的观测结果；N为移动的平均项目数。

针对Tn+1时刻的预测，建立预测模型如图3所示，采用的方法是依据前面4个相邻的历史数据来预测下一个数据。Xn、Xn-1、Xn-2、Xn-3分别是Tn、Tn-1、Tn-2、Tn-3的实际交通流量数据，隐含层数量为1。

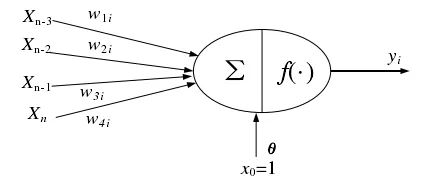
图3 预测模型Figure 3 Forecast model

（2）中间隐含层神经单元个数选择

设输入层神经单元个数为 InNum，输出层神经单元个数有OutN um ，MidNum 为中间层神经单元个数，的取值范围1 ～10，其公式为：

2.2 基本算法流程

（1）网络初始化：随机初始化小波函数伸缩因子，平移因子，以及网络权值和学习速率。

（2）样本训练：把样本分为训练样本和测试样本，训练样本用于训练网络，测试样本测试精度。

（3）预测输出：把训练样本输入网络，计算网络预测输出，并计算网络输出和期望输出误差。

（4）权值修正：根据误差修正网络权值和小波参数，使网络预测值逼近期望值。

（5）判断算法是否结束，如没有结束返回步骤3。

3 小波神经网络模型仿真分析

选择某路段四天内的交通流量，每隔15分钟记录一次，一共采集384个数据。用前三天的数据训练网络结构，第四天的数据作为测试。输入节点数同样为4个，隐含层节点数为6，输出层为1，小波神经网络预测模型的仿真结果与测试数据误差百分比如图4、5所示：

图4 寐波神经网络模型预测值与真实值密比Figure 4 Comparison of predicted and true values of wavelet neural network model

本次实验通过五个评价指标来反应该模型的预测效果如表1所示：

表1 寐波神经网络预测评价Table 1 Prediction and evaluation of wavelet neural networks

从图5中我们可以清晰地看到大部分测试数据误差百分比都在10%以内。

图5 测试样本与真实值的绝密误差百分比Figure 5 Percentage of absolute error between the test sample and the true value

4 两种预测模型仿真结果对比

将附加动量项BP神经网络预测和小波神经网络预测的结果与真实值做对比，比较结果如图6所示：

图6 两种预测模型预测结果与真实值的比较Figure 6 Comparison of the predicted results with the real values of the two predictive models

从仿真实验可以看出，小波神经网络对于短时交通流量预测相比附加动量项BP神经网络预测具有更高的精度。为了比较两种算法在迭代次数相同时的性能，本文分别采取了迭代次数在三百次，五百次，一千次的性能结果比较。

表2 训练三百次两种算法性能分析Table 2 Estimate the results of 300 predictions

表2表示的是两种算法在训练三百次的性能比较，表3是训练五百次结果分析，表4是训练一千次的结果分析。

表3 训练五百次两种算法性能分析Table 3 Estimate the results of 500 predictions

表4 训练一千次两种算法性能分析Table 4Estimate the results of 1000 predictions

为了更加清晰明了地得到小波神经网络与附加动量BP神经网络预测模型的性能对比。在两种算法通过不同的训练次数后，对其训练过程中的性能做比较。

图7是小波神经网络与附加动量BP神经网络预测模型在四种训练次数中平均绝对百分误差MAPE的变化。从图7可以发现，当训练次数从三百次到一千次过程中，两个预测模型的MAPE都呈下降趋势。由于小波神经网络从三百次都比附加动量BP神经网路精度要高，所以其精度调整变化不大，其比附加动量BP型神经网络平均相对误差变化的要慢。但从三百次到一千次整个过程，附加动量BP型神经网络的MAPE都比小波神经网络的要高出许多。

图7 在不同的迭代次数下 MAPE 值的密比Figure 7 Comparison of MAPE values for two models under different iterations

图8 在不同的迭代次数下训练时间的密比Figure 8Comparison of training time for two models under different iterations

图8是两个预测算法在四种训练模式下STT变化。可以发现，当训练次数从三百次到一千次过程中，两个预测模型的STT都呈上升趋势。附加动量BP神经网络比小波神经网络训练时间稍短，虽有误差并没有改变输出预测的值，它并没有造成时间的指数性增长。图9给出了两种预测模型各个测试样本的绝对误差百分比与误差的比较。

图9 两种预测模型各个测试样本的绝密误差百分比比较Figure 9 Comparison of Absolute Errors for Each Test Sample in Two Predictive Models

图10 附加动量BP型神经网络和（wnn）寐波神经网络误差分析图10 BP neural network and wavelet neural network (WNN) error analysis

从图9中可以明显看到小波神经网络预测模型的各个测试样本的百分比误差基本在10%之下，而附加动量BP神经网络多数10%以上。图10可以更直观地看出小波神经网络比附加动量BP神经网络误差小，小波神经网络引入小波分析的思想对数据良好的处理能力，对预测精度有很大的提高。

5 结束语

依照预测结果，结合附加动量BP神经网络的仿真结果进行了对比。选取三种预测结果评价指标：平均相对误差（MAPE）、平均绝对误差(MAE)和训练样本时间。在适当交通路段，分别对两种模型进行了各自的实验，两次实验主要是迭代次数不同，次数分别为三百次、五百次、一千次，然后根据实验结果，以及作图分析指出小波神经网络模型的预测能力更高，在系统实时性要求中，在可接受的范围之内，但其精度比附加动量BP神经网络高出不少，因此综合分析，小波神经网络算法预测短时交通流量更为适合。

[1]吴伟. 基于改进遗传算法的神经网络结构优化研究[D]. 苏州大学,2012.

[2]Inoue M,Nagayoshi. A chaos neuro-computer. Physics Letters-A,2011,158(8)： 373-376.

[3]沈小峰. 交通流量短时预测的算法研究[D]. 浙江工业大学,2015.

[4]谭政. 城市道路交通流预测及应用[D]. 华南理工大学,2012.

[5]Peterson R. Study on Urban Intersection Traffic Flow Forecasting and Traffic Signal Control[J]. Applied Mechanics and Materials. 2012,22(135)： 3-12.

Short-term Freeway Traffic Flow Prediction Based on Wavelet Neural Network

REN Xiaoxia1*,SONG Haiming2
(1. Shanxi Technology and Business University,Shanxi Linfen,030003,China; 2. Economic and Technical Research Institute,State Grid Xinjiang Electric Power Corporation,Xinjiang Urumqi 830011,China)

BP neural network,an artificial intelligence algorithm,has ability of self-learning and approximation for nonlinear data. It’s easy to be trapped in local minimum,due to the use of gradient descent method. For further improvement of the prediction accuracy,we use the time-frequency characteristics of wavelet to reduce the sensitivity of network structure to data,achieving good prediction.By wavelet decomposition and reconstruction for traffic flow data we can get the low frequency approximation part and high frequency random part,and then based on the analysis of various models,we select the effective manner of model or the way model combined .Finally,a simulation system will be established by the measured traffic flow data ,the results show that the model can effectively improve the accuracy of short-term traffic flow prediction.

short-term traffic flow prediction; wavelet neural network; BP neural network

TP18

A

1672-9129(2017)06-0037-04

10.19551/j.cnki.issn1672-9129.2017.06.012

任晓霞,宋海明. 基于小波神经网络短时交通流量预测[J]. 数码设计,2017,6(6)： 37-39.

Cite：REN Xiaoxia,SONG Haiming. Short-term Freeway Traffic Flow Prediction Based on Wavelet Neural Network[J]. Peak Data Science,2017,6(6)： 37-39.

2017-02-16；

2017-03-07。

任晓霞（1990-），女，山西省临汾市襄汾县、职务：教师、学历：研究生。

Email：704505351@qq.com