航天器分布式有限时间编队方法

康珅，单家元

（1.北京理工大学 宇航学院，北京 100081；2.飞行器动力学与控制教育部重点实验室，北京 100081）

航天器分布式有限时间编队方法

康珅1,2，单家元1,2

（1.北京理工大学 宇航学院，北京 100081；2.飞行器动力学与控制教育部重点实验室，北京 100081）

以二阶积分环节作为单体航天器动力学模型，在固定通信拓扑的基础上，假设每个航天器仅获取相邻航天器的速度位置信息，设计了分布式有限时间跟踪控制算法，并证明了算法的有效性。在该算法的基础上，采用了虚拟结构和阶级控制方法，使第一阶级航天器接受虚拟领队形成的虚拟结构信息，次级航天器接受上一级航天器信息，给出了有限时间编队方法，并通过数值仿真验证了该编队算法。

分布式控制；航天器编队；有限时间收敛；阶级控制

0 引 言

航天器编队是由若干颗航天器组成编队，保持一定相对位置关系，各航天器间密切联系，共同完成某项空间任务的飞行技术，是近年来空间科学领域研究热点之一。编队系统一般由一颗主航天器和几颗围绕其飞行的从航天器组成，各航天器之间距离较近，从几十米到几十千米。航天器编队具有成本低、系统冗余性和鲁棒性强、自主性高等特点，具有广阔的应用前景。分布式控制是2005年后出现的控制方式，旨在减轻通信负担，增强被控对象的自主性。在分布式控制策略中，每颗航天器均具有独立的局部决策能力，仅采用相邻单位信息，应用相互的通信网络协调，便可形成期望的编队运动。典型的协同控制方式有主从式、基于行为和虚拟结构的方式等。

早期的航天器位置编队主要以领从方式为主，更多考虑轨道动力学对于航天器编队的影响。在轨道动力学的基础上，多采用HCW（Hill-Clohessy-Wiltshire）方程等模型，附加控制约束或控制指标，进行分析设计[1-4]。分布式控制出现后，大量研究偏向于将动力学模型简化为二阶积分环节，侧重通信拓扑特性以及分布式控制对编队的影响，文献[5]讨论了通信延时对于一致性的影响；文献[6]～文献[7]在有向图的基础上，设计了切换拓扑下的跟踪控制器，并在一定切换模式下证明了其有效性；文献[8]基于二阶积分环节和切换拓扑，设计了分布式观测器用于提取速度信息，并完成了一致性控制器的设计。在阵型控制方面，文献[9]引入虚拟结构的概念，实现了航天器编队的分布式姿态控制；文献[10]针对一阶积分模型设计了有限时间稳定的阵型控制算法。

本文以二阶积分环节为模型，设计了航天器编队的分布式有限时间跟踪控制器，同时采用虚拟结构和阶级控制方法，实现了有限时间的阵型控制，并通过数值仿真验证了算法的有效性。

1 预备知识

为突出有限时间控制器设计，本文航天器编队问题的动力学系统如下

1.1 运算符号

1.2 代数图论

本文采用无向图描述航天器之间的通信拓扑。对于无领从关系的多航天器系统，认为每个航天器为顶点，其间的信息交互由无向图G表示，记为，其中为所有顶点构成的集合，为所有边构成的集合。是图G的邻接矩阵，定义为

对于带有权重的邻接矩阵A，其元素aij定义为当时，即航天器i可获取航天器j的信息时，；反之，。对于无向图，有aij=aji。

1.3 定义及引理

引理1[11]对于矩阵，若且，无向图G的拉普拉斯矩阵是正定的，当且仅当无向图G是连通的。

引理2[12]考虑系统

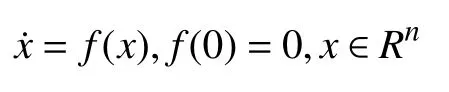
定义1（有限时间跟踪）对于系统（1），控制律可实现有限时间跟踪控制，当且仅当存在某一有限时间t*，有

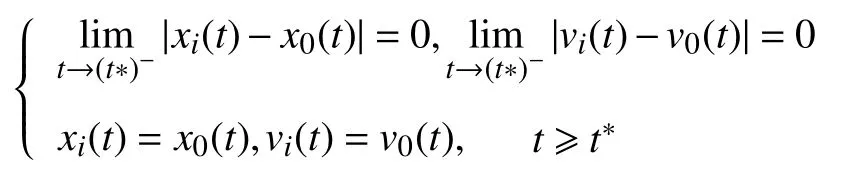
2 主要结果

2.1 有限时间跟踪控制

考虑如下跟踪控制律

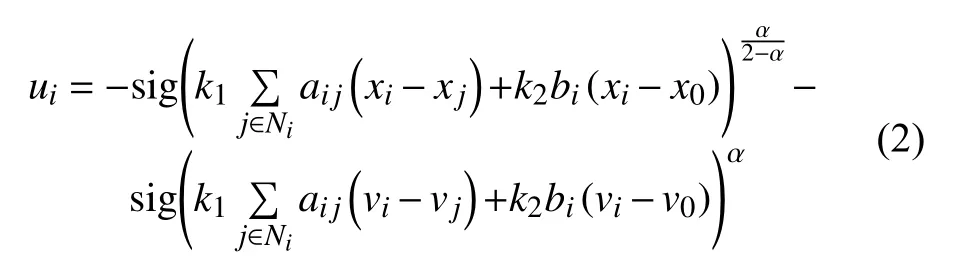
定理1若表示航天器间通信拓扑的无向图G为连通图，且至少有一个航天器能接收到领队信息，则在控制律（2）的作用下，系统（1）可以实现有限时间跟踪控制。

证明：令，并将控制律式（2）带入式（1），可得

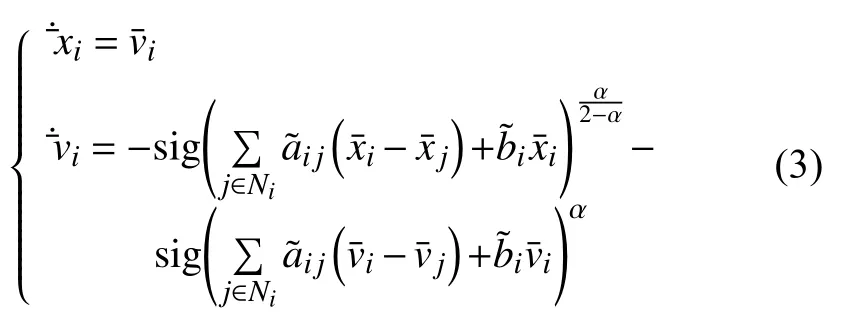
将上述变换代入（3），可得误差系统

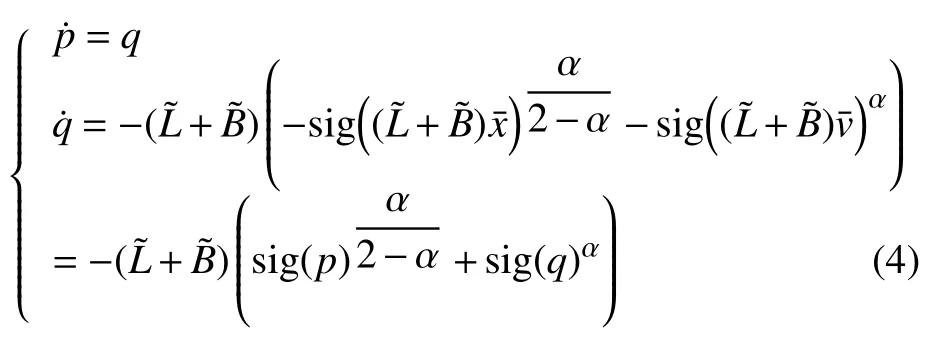
取备选李雅普诺夫函数

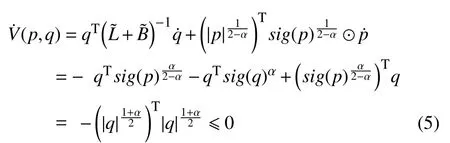
根据式（4）和式（5）可得如下性质

由式（6）可知V径向无界。取，代入式（6）和式（7），可得

综上所述，完成了对定理1的证明。

2.2 有限时间阵型控制

本节采用虚拟结构和阶级控制方法[9]，对航天器编队进行阵型组织。首先将航天器群分为数个阶级，第1阶级航天器直接接受虚拟领队的信息，第2阶级航天器则接受第1阶级航天器的信息作为领队信息，以此类推。

定理2若表示第i级航天器间通信拓扑的图Gi为连通图，且第i级中至少有一个航天器能接收到上一级航天器的信息，则在控制律式（2）的作用下，每一级航天器都可以实现有限时间跟踪控制。

证明同定理1。

3 仿真结果

3.1 有限时间跟踪

本例侧重体现有限时间跟踪控制效果，无具体物理意义。航天器间通信拓扑及初始状态如图1所示。仿真参数取α= 0.6，k1= 1，k2= 3。由图2及其局部放大图可知，t= 34.5 s时，各航天器均无控制输入，此时由图3可知，航天器位置速度成功跟踪领航天器状态。

3.2 阵型控制

图1 航天器间通信拓扑及各航天器初始状态Fig.1 The communication topology and initial states of spacecrafts

图2 各航天器的控制输入变化曲线Fig.2 The control input of spacecraft

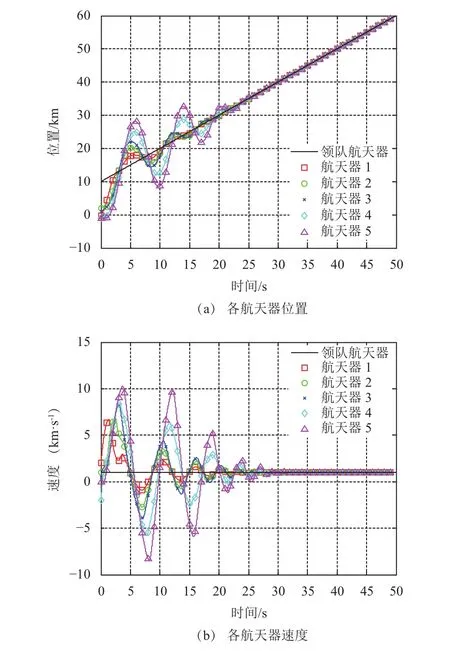
图3 各航天器的位置和速度变化曲线Fig.3 The position and velocity profiles of the spacecraft in the formation

如图4所示，示例的阵型控制分为2个阶级，第1阶级直接接收来自虚拟领队的信息，跟踪虚拟领队形成的虚拟结构；第2阶级则有部分航天器接受第1阶级的信息，根据分布式原则自组织阵型。

图4 阶级控制通信拓扑Fig.4 Communication topology with hierarchies

在控制参数同上例的情况下，对阵型控制进行三维数值仿真。令虚拟领队形成一个有4个顶点的虚拟结构，第1阶级中的航天器接受该虚拟结构信息，并实行跟踪；第2阶级中的部分航天器接受第1阶级航天器的信息，根据固定拓扑，形成1个四面体编队，如图5所示。其中虚拟领队以v0= 1 m/s的速度匀速运动，t=100 s时，令虚拟结构以0.05 rad/s的角速度进行转动，t= 200 s时停止转动。可见在虚拟结构开始转动的35 s内，跟踪轨迹有轻微的震荡过程，与上例中有限时间跟踪的结论相符合。由此验证了该编队算法的有效性。

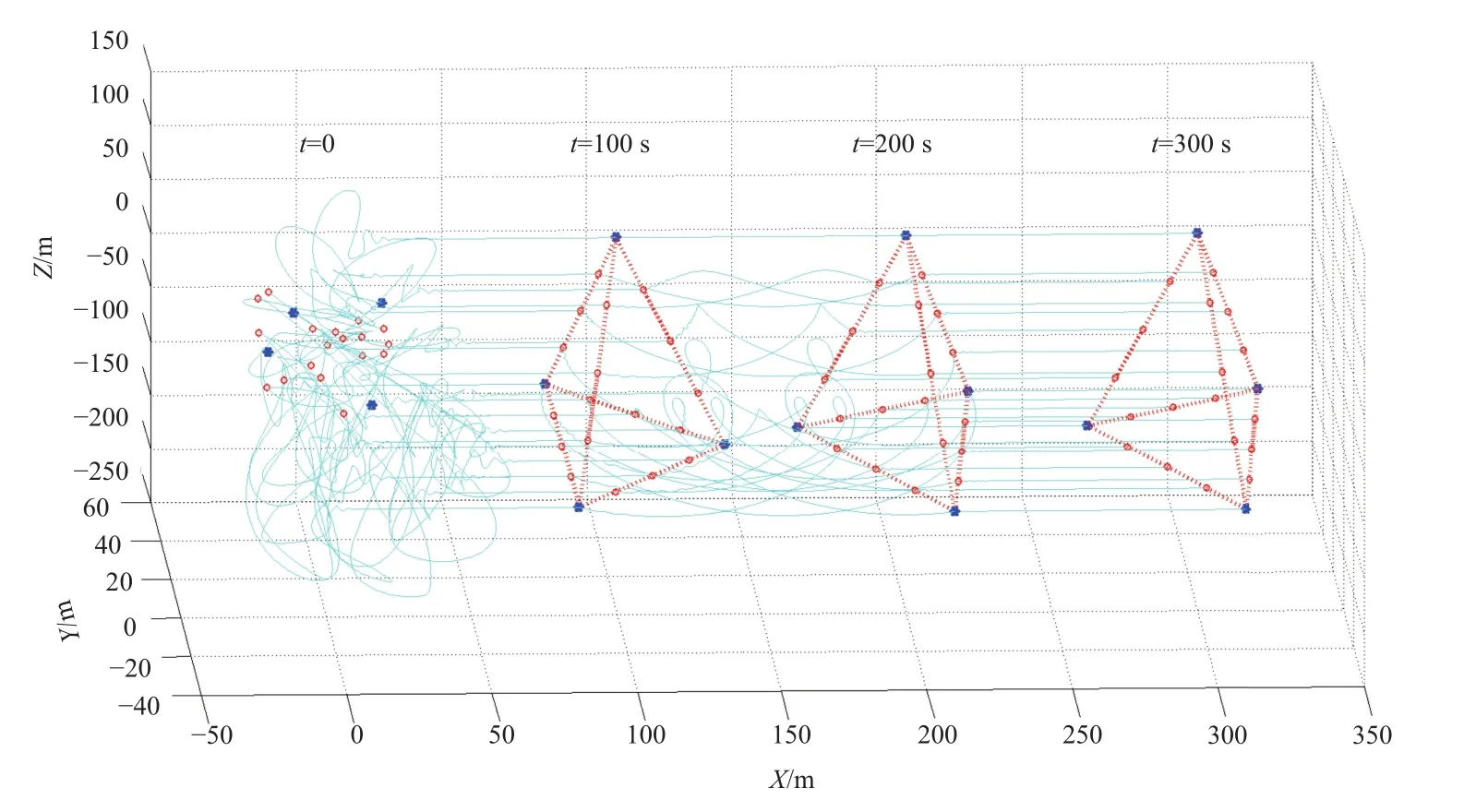
图5 空间编队阵型示意图Fig.5 The formation flying in deep-space environment

4 结 论

本文将单体航天器动力学模型简化为二阶积分环节，在无向图的基础上，假设每个航天器仅获取相邻航天器的速度位置信息，设计了分布式有限时间跟踪控制算法，并证明了该算法的有效性。在有限时间跟踪控制算法，采用虚拟结构和阶级控制方法，使第1阶级航天器接受虚拟领队形成的虚拟结构信息，次级航天器接受上一级航天器信息，给出了有限时间编队方法，并通过数值仿真，形成了四面体编队，并实现了有限时间队形变换，验证了编队方法。后续研究将以编队中的避撞问题为重点，进一步提高编队算法的实用性。

[1]Lim H C，Bang H.Adaptive control for satellite formation flying under thrust misalignment[J].Acta Astronautica，2009，65（1）：112-122.

[2]De Queiroz M S，Kapila V，Yan Q.Adaptive nonlinear control of multiple spacecraft formation flying[J].Journal of Guidance，Control，and Dynamics，2000，23（3）：385-390.

[3]Slater G L，Byram S M，Williams T W.Collision avoidance for satellites in formation flight[J].Journal of Guidance，Control，and Dynamics，2006，29（5）：1140-1146.

[4]Ulybyshev Y.Long-term formation keeping of satellite constellation using linear-quadratic controller[J].Journal of Guidance，Control，and Dynamics，1998，21（1）：109-115.

[5]Sun Y G，Wang L.Consensus problems in networks of agents with double-integrator dynamics and time-varying delays[J].International Journal of Control，2009，82（10）：1937-1945.

[6]Guo W，Lv J，Chen S，et al.Second-order tracking control for leader-follower multi-agent flocking in directed graphs with switching topology[J].Systems & Control Letters，2011，60（12）：1051-1058.

[7]Lu X，Chen S，Lv J.Finite-time tracking for double-integrator multiagent systems with bounded control input[J].IET Control Theory &Applications，2013，7（11）：1562-1573.

[8]Hong Y，Chen G，Bushnell L.Distributed observers design for leaderfollowing control of multi-agent networks[J].Automatica，2008，44（3）：846-850.

[9]Cong B L，Liu X D，Chen Z.Distributed attitude synchronization of formation flying via consensus-based virtual structure[J].Acta Astronautica，2011，68（11）：1973-1986.

[10]Xiao F，Wang L，Chen J，et al.Finite-time formation control for multiagent systems[J].Automatica，2009，45（11）：2605-2611.

[11]Ni W，Cheng D.Leader-following consensus of multi-agent systems under fixed and switching topologies[J].Systems & Control Letters，2010，59（3）：209-217.

[12]Zhou D，Sun S，Teo K L.Guidance laws with finite time convergence[J].Journal of Guidance，Control，and Dynamics，2009，32（6）：1838-1846.

Distributed Finite-Time Control Method for Formation Flying

KANG Shen1,2，SHAN Jiayuan1,2
（1.School of Aerospace Engineering,Beijing Institute of Technology,Beijing 100081,China；2.Key Laboratory of Dynamic and Control of Flight Vehicle,Ministry of Education,Beijing 100081,China）

In this paper，a dynamic model of single spacecraft is simulated by a double integrator and the communication topology is assumed fixed.Based on the information exchanges among neighbors，the distributed finite-time control protocol is designed and mathematically verified.Adopt the presented control protocol and combined with virtual structure and hierarchical protocol，the formation algorithm is designed，where in a group spacecraft on a lower level takes orders from spacecraft on a higher level.The numerical simulation is conducted，verifying the effectiveness of the proposed method.

distributed control；formation flying；finite-time stable；hierarchical control

V11

A

2095-7777（2017）04-0390-05

10.15982/j.issn.2095-777.2017.04.0013

康珅，单家元.航天器分布式有限时间编队方法[J].深空探测学报，2017，4（4）：390-394.

Reference format：Kang K，Shan J Y.Distributed finite-time control method for formation flying[J].Journal of Deep Space Exploration，2017，4（4）：390-394.

2015-09-25

2017-05-02

康珅（1990- ），男，博士研究生，主要研究方向：协同控制、飞行器制导、动力学建模与仿真等。

通讯地址：北京市中关村南大街5号，北京理工大学宇航学院飞行器控制系（100081）

E-mail：seankang90@gmail.com

[责任编辑：杨晓燕，英文审校：朱恬]