输电网规划全寿命周期综合成本计算研究

孟遂民 刘 闯 卢银均 陈思凡 杨鸽子 向乃瑞

(1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2.国网湖北省电力公司 荆门供电公司，湖北 荆门 448000)

输电网规划全寿命周期综合成本计算研究

孟遂民1刘 闯1卢银均2陈思凡1杨鸽子1向乃瑞1

(1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2.国网湖北省电力公司 荆门供电公司，湖北 荆门 448000)

为比较输电网规划方案的经济性，提出了一种基于全寿命周期成本，在规划期内逐年计算各项成本的线路综合成本计算方法．在计算线路故障率时，根据故障后果明确划分故障类型，并采用改进的灰色GM(1，1)模型对线路故障率进行中长期预测，使线路运维成本计算更准确．在进行经济方案优选时，利用区间分析法计算输电线路综合成本，消除单一定值引起的计算误差，能够更好地比较各方案的优劣性．根据实际工程算例验证文中综合成本模型在新旧混合线路规划中的通用性和有效性．

输电网规划； 全寿命周期； 综合成本； 灰色预测

为保证电网的可持续发展，输电网规划不仅需要满足日益增长的供电需求，更应该充分考虑其经济性．全寿命周期成本(life cycle cost，简称LCC)是指在产品寿命周期内，产品投资、运行损耗、运行维护、故障损失和退役回收等各项费用总和[1]．LCC最初在铁路、军事行业应用广泛[2]，近年，LCC 技术逐渐向电力系统推广应用．文献[3]建立以电网全寿命周期成本最小为目标函数的电网规划数学模型，该模型对电网全寿命周期成本划分不够明确；文献[4]提出输电线路全寿命周期总成本和各主要部件的成本预测模型，但没有考虑不同类型故障率对线路运维成本的影响；文献[5]根据全寿命周期理论建立配电设备的全寿命周期故障率数学模型，该模型未明确划分故障类型．

在进行规划方案比较时，计算全寿命周期成本要比只考虑建设成本更合理，但全寿命周期成本模型在实际应用中还存在一些不足．输电线路故障率与线路投运时间有关，若不考虑线路故障率会对运维成本的计算造成较大的误差[6]，在计算新旧混合的输电线路全寿命周期成本时，不同役龄的线路运维成本应分别计算，不能直接使用LCC模型．因此，要提高输电线路经济方案优选的准确性，还有很多亟待解决的难题．

本文在输电线路全寿命周期成本构成的基础上，将规划年限作为边界条件，提出了一种逐年计算各项成本并考虑规划期末现值的线路综合成本计算方法．根据故障后果对线路故障类型进行划分，采用改进的灰色预测模型分别计算各类故障率，使输电线路运维成本的计算结果更加准确，并结合区间分析法进行经济方案优选．最后通过工程算例验证了对新旧混合线路进行规划方案优选时使用综合成本模型更合理．

1 输电线路综合成本

传统LCC理论认为，输电线路LCC模型是指考虑整条线路的初始投资成本，该线路整个生命周期内的运行、维护、检修成本，以及拆除时的折现收益．但输电线路运行期间可能因为生产实际需要部分线路会被改造或重建，遇到这种情况时LCC模型并不适用．

为此，在输电线路LCC模型构成的基础上，提出一种在规划期内逐年计算各项成本，并扣除规划期末现值的输电线路综合成本计算模型．在进行方案优选时，分别计算每种方案在规划期内的线路综合成本，成本越低说明该方案的经济性越好．其计算模型为

其中，N为规划年限，r为考虑时间因素的资金折现率；CIi、COi、CMi、CFi分别为输电线路在规划期第i年的建设投资成本、运行损耗成本、运行维护成本及故障损失成本；CD为第N年该方案所有设备经折旧后的退役回收成本．所有成本均为规划年初预算．

2 综合成本计算模型

在进行输电网规划时，对于新旧混合线路，其全寿命周期的起点和终点难以认定，无法计算该线路的全寿命周期成本．因此考虑到输电线路在实际运行中可能出现新增或拆除等情况，综合成本计算模型在线路规划中更加可行．

2.1 区间分析法

在计算输电线路综合成本时，使用了大量的经验数据和统计数据，若采用单一定值计算时会引起较大误差，因此本文采用区间分析法对各项成本进行计算．

P(a>b)=

当P(a>b)>0.5时，b优于方案a．

2.2 建设投资成本的计算

建设投资成本是指输电线路在规划期年初的投入成本和未来在规划期内改造该线路所需的投资成本．建设投资成本的模型为：

其中，mi为第i年需新建线路条数；cl为单位长度线路的投资建设成本；lj为第j条新建线路的长度；ui为第i年需报废线路条数；dl为单位长度线路的退役回收成本；lk为第k条拆除线路的长度．

2.3 运行损耗成本的计算

运行损耗成本可根据线路运行相关经验数据和线路长度进行计算，计算模型为：

其中，kj为第i年由于改造新建的第j条线路在建设年投入运行的时间系数，如该线路投运于建设年6月份，则kj=(12-6)/12=0.5；cO.l.j为第i年第j条线路单位长度运行损耗成本；ni为在规划期内第i年之前建设的输电线路条数．

2.4 运行维护成本与故障损失成本的计算

运行维护成本与故障损失成本均根据线路运维部门的经验数据和输电线路故障率相结合进行计算．对改造后不同役龄段的新、旧混合线路需要分别计算故障率．可根据故障后果对故障分级，将故障分为Ⅰ级故障(缺陷级故障)、Ⅱ级故障(失效级故障)和Ⅲ级故障(事故级故障)等3类[8]，使线路运维成本和故障损失成本的计算结果更准确．

运行维护成本的计算模型为：

故障损失成本的计算模型为：

其中，p=1，2，3分别表示Ⅰ级故障、Ⅱ级故障和Ⅲ级故障；λi.j.p为第j条线路在第j年的p级故障率，单位为次/(a·100 km)；cM.l.p为p级故障的平均运维成本；cF.l.p为p级故障的平均故障损失成本．

2.5 退役回收成本的计算

退役回收成本是指输电线路退役折旧后的价值，即折现值．投运时间不同的线路拆除时回收价值不同，需要分别计算．本文采用加速折旧思想计算退役后的现值[9]，具体方法是当线路役龄超过某一定值时，退役回收成本直接采用线路残值；否则，采用直线折旧方法计算该成本．退役回收成本的计算模型为：

其中，CCi为第i年新建线路的总建设投资成本，q为残值百分比，1-q为可折旧设备的百分比；X为线路役龄阀值，线路役龄超过该值时，折旧后的现值视为残值．

3 输电线路故障率预测模型

在对综合成本模型进行求解时，输电线路各类故障率是计算运行维护成本和故障损失成本的必要条件．若非极端天气出现，同一线路的故障率随役龄的增长呈现一定的变化规律[10]．灰色预测是指在一定方位内变化的事物且事物变化过程与时间有关的一种预测方法[11]．改进的灰色预测模型不仅具有所需历史数据少、预测精度高、计算简便等优点，还能进行中长期预测[12]．因此可采用改进的灰色预测模型粗略计算线路各类故障率．

3.1 线路故障率计算模型

本文中所说的线路故障率是指某条线路每一百公里长的线路在一年运行过程中发生故障的次数，计算时应根据故障后果对各类故障进行分类统计，可按下式计算：

式中，Np表示某线路运行区间发生p级故障的次数，lp表示该线路总长度．

3.2 改进的灰色GM(1，1)故障率预测模型

已知历年某条输电线路Ⅰ级故障率的原始数据：x(0)=[x(0)(1)，x(0)(2)，…，x(0)(n)]，对x(0)进行一阶变换，得到新序列x(1)=[x(1)(1)，x(1)(2)，…，x(1)(n)]，其中，

并用x(1)产生紧邻均值序列Z(1)=[z(1)(1)，z(1)(2)，…，z(1)(n)]，其中

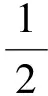
预测模型GM(1，1)的白化微分方程如下

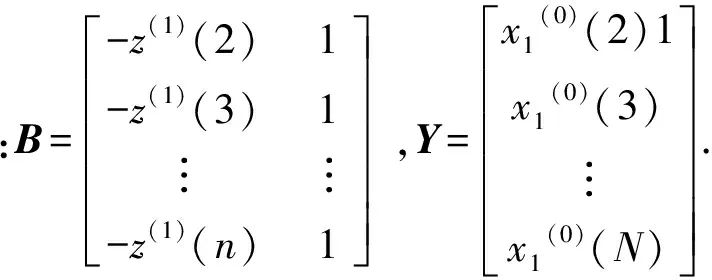
则微分方程的解为

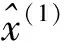
还原即可得到预测方程

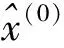
利用上述过程完成一次预测后得到x(0)(n+1)，并将x(0)(n+1)放入原始数据序列中，同时在原始数据中去掉x(0)(1)，再用x(0)=[x(0)(2)，x(0)(3)，…，x(0)(n+1)]作为原始数据x(0)，重新建立GM(1，1)模型，如此反复并依次递补，直至完成预测目标．

3.3 预测精度检验

根据C和P值确定预测模型精度是否合格，精度分级标准参照表1．

表1 灰色预测精度等级表

当预测模型精度偏低时，可利用故障率残差序列进行建模，对上述GM(1，1)预测模型进行修正[13]．

4 算例分析

图1是某地区110 kV部分输电网络，由于该地区负荷连续增长，根据预测，需要新建4号变电站并新建部分输电线路，考虑到技术和环保等因素，最终提出两种可行的规划方案．方案1将4号变电站建在线路Ⅰ附近，以小开口接线方式接入线路，即DE段线路长度可忽略；方案2考虑到线路走廊问题，需将4号变电站建在距离线路Ⅱ附近，以大开口接线方式接入，即DE段线路必须拆除．具体规划示意图如图1所示．

图1 线路规划示意图

线路Ⅰ长度为20.2 km，从2003年6月开始运行；线路Ⅱ长度为36.1 km，从1998年2月开始运行．根据该地区110 kV输电线路的相关运行经验分析，得出线路Ⅰ将在15年后拆除，线路Ⅱ将在8年后拆除．由于新建的4号变电站在上述两种方案中的建设、运行与维护成本相近，因此变电站费用无需计算．另外线路Ⅰ在1方案中几乎无变化，为简化计算，故只需对两方案中的新建线路CD、CE以及方案B中的拆除线路DE．假设新建线路的导地线、杆塔与绝缘子串等型号与原线路相同，线路役龄阈值均设为20年．

方案1计划在规划年的5月份完工并投入运行，方案2计划在规划年的11月份完工并投入运行．表1列出了110 kV输电线路相关经济参数指标[14-15]．

表2 110 kV输电线路相关经济参数指标

求解规划方案综合成本的其他参量均已确定，下面根据改进的灰色GM(1，1)模型计算方案1中未拆除线路DE段的各类故障率．首先进行预测模型数据筛选，表3列出了线路Ⅰ从2000～2015年的故障率统计数据，分别以2000～2014年的Ⅰ级故障率数据和2005～2014的Ⅰ级故障率数据构建GM(1，1)模型1和模型2．

表3 线路Ⅰ历年Ⅰ级故障率[单位：次/(a·100 km)]

根据上述精度检验公式，分别计算两模型精度见表4．从表4可知，模型2精度更高．故选择模型2数据作为改进的GM(1，1)基础模型．

表4 模型精度检验表

运用Matlab编程计算可得预测方程为

利用上述方程得到2005～2014基础模型的模拟值，见表5．

表5 基础模型模拟值 [单位：次/(a·100 km)]

用后验差法对改进的GM(1，1)基础模型和后续预测模型进行检验，结果均良好．用模型预测未拆除段线路的Ⅰ级故障率为0.801 2次/(a·100 km)，与2015年该线路Ⅰ级故障率实际值0.796 3次/( a·100 km)的相对误差为0.61%，可见预测模型精度很高．

利用上述模型预测出方案1中未拆除线路DE段未来五年内的Ⅰ级故障率如图2所示．

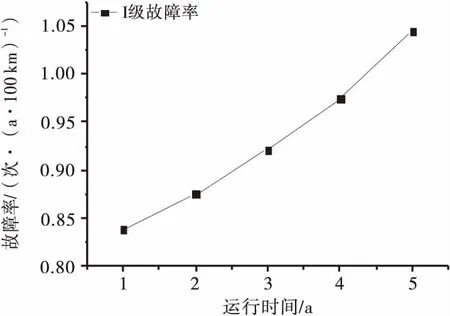
图2 未来5年内Ⅰ级故障率预测值

采用相同的方法，可求得未拆除线路DE段Ⅱ级故障率如图3所示，Ⅲ级故障率如图4所示．

图3 未来5年内Ⅱ级故障率预测值

图4 未来5年内Ⅲ级故障率预测值

由于新建线路长度较短，且线路1和线路2所处的运行环境基本相同，因此两方案中的新建线路故障率可根据线路1和线路2历史统计数据确定，根据输电线路综合成本计算方法，得到5年规划期时的各成本见表6．

表6 5年规划期各成本区间 (单位：万元)

由表6可知，方案1综合成本最少为354万元，最多为606万元；方案2综合成本最少为224万元，最多为516万元．区间运算后可得，方案2相对方案1的优势度为0.822，因此优先考虑方案2．

当该规划期为10年时，由于线路2将在第8年全部拆除，方案1中线路DE的故障率应分为拆除前和拆除后分别计算，1～7年的故障率可采用上述模型计算，第9、10年的故障率由线路2的历史数据得出，两方案中新建线路CE、CF的各类故障率仍采用历史统计数据．需要指出的是，方案2中需要拆除线路DE段，而线路Ⅱ中剩余部分线路在两种规划方案中都需要重建，故方案1在第8年时需要增加DE段线路的建设投资成本．具体计算结果见表7．

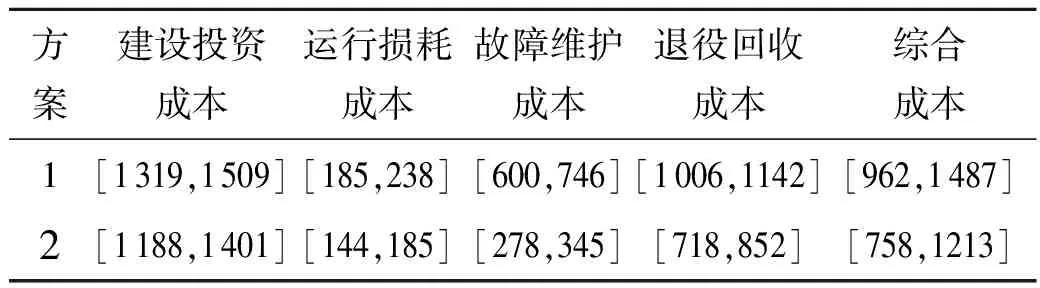
表7 10年规划期各成本区间 (单位：万元)

由表7可知，方案2的综合成本的最小值和最大值仍小于方案1．根据区间运算法则，方案2相对方案1的优势度为0.868，较5年规划期中方案1的优势度有所上升，可见方案2的优势越来越明显．

由此可见，综合成本计算模型适用于不同时间长度规划方案的经济优选，与区间分析法相结合时，能够更好地比较各方案的经济性．

5 结 语

本文基于输电网规划全寿命周期成本，对输电线路各项成本进行精细划分，提出了一种线路综合成本计算方法，得到如下结论：

1)综合成本计算模型考虑了线路在实际运行中出现部分拆除或新增的情况，对役龄不同的线路分别逐年计算规划年限内的各项成本，比直接采用LCC模型计算更合理．

2)运用改进的灰色GM(1，1)模型计算出本文实例中方案1未拆除线路2015年的Ⅰ级故障率为0.801 2次/(a·100 km)，与真实值相比误差为0.61%，预测模型精度较高，线路运维成本的计算更准确．

3)在对实际线路规划方案进行优选时，运用区间分析法计算得到方案2较方案1在5年规划期和10年规划期的优势度分别为0.822和0.868，说明方案2比方案1的经济性更好．

[1] Yin H，Fan L，Miao Z．Coordination between DFIG-Based Wind Farm and LCC-HVDC Transmission Considering Limiting Factors[J]．Energytech，2011 IEEE 2011：1-6．

[2] John A．Kuprenas Rroject Management Actions To Improve Design Phase Cost Performance[J]．Journal of Management In Engineering， 2003．

[3] 鲁国起，张 焰，祝达康．全寿命周期成本及其在电网规划中的应用[J]．现代电力，2009，23(15)：77-81．

[4] 钟小平，金伟良．输电线路全寿命周期设计理论方法[J]．结构工程师，2011，27(5)：6-16．

[5] 黄道姗．基于设备全寿命周期的配电系统可靠性评估方法[J]．电力科学与技术学报，2016，31(2)：72-78．

[6] Benato R．Napolitano D．Overall Cost Comparison between Cable and Overhead Lines Including the Costs for Repair After Random Failures[J]．IEEE Transactions on Power Deliwery．2012，27(3)：1213-1222．

[7] 江修波，吴文宣，陈祥伟．区间分析法在电力变压器全寿命周期成本模型中的应用[J]．电力自动化设备，2011，31(9)：50-53．

[8] 国家电网公司．国家电网公司安全事故调查规程[S]．北京：中国电力出版社，2012．

[9] 方欢欢，程浩忠，辛洁晴，等．配电网规划评估指标体系[J]．电力系统及其自动化学报，2013，25(6)：106-111．

[10] 潘乐真，张 焰，俞国勤，等．状态检修决策中的电气设备故障率推算[J]．电力自动化设备，2010，30(2)：91-94．

[11] 孟祥星，田成微，冬 雷，等．灰色理论用于风力发电容量中长期预测的研究[J]．电力系统保护与控制，2011，39(21)：81-85．

[12] 张 莉，吉培荣，杜爱华，等．中长期电力负荷预测的几种灰色预测模型的比较及应用[J]．三峡大学学报：自然科学版，2009，31(3)：41-45．

[13] 刘思峰，谢乃明，等．灰色系统理论及其应用[M]．4版．北京：科学出版社，2008．

[14] 国家电网公司．国家电网公司电网检修运维和运营管理成本标准(试行)[S]．2009．

[15] 国家电网公司．国家电网公司输变电工程通用造价输电线路分册[S]．北京：中国电力出版社，2010．

StudyofLifeCycleComprehensiveCostofTransmissionNetworkPlanning

Meng Suimin1Liu Chuang1Lu Yinjun2Chen Sifan1Yang Gezi1Xiang Nairui1

(1. College of Electrical Engineering & Renewable Energy, China Three Gorges Univ., Yichang 443002, China; 2. State Grid Jingmen Power Supply Company, Jingmen 448000, China)

In order to compare economical schemes of transmission network, a method for calculating the comprehensive cost of the network based on the life cycle cost is proposed. While computing failure rate of the line, the fault types are clearly divided according to the fault ruselt; and the better grey GM (1,1) model is used to predict the fault rate; so that the cost of the operation and maintenance is calculated more accurately. While carrying out optimized selection of economical schemes, the comprehensive cost of transmission line is calculated by interval analysis method to eliminate the calculation error caused by the single value; and then the advantages and disadvantages of every scheme can be better compared. According to the engineering example, this thesis verifies universality and validity of comprehensive cost model in mixed new and old line planning.

transmission network planning; life cycle; comprehensive cost; gray prediction

2017-03-14

新能源电力系统国家重点实验室开放基金(LAPS14016)

孟遂民(1957-)，男，教授，研究方向为输电线路工程．E-mail：msm@ctgu.edu.cn

10.13393/j.cnki.issn.1672-948X.2017.05.017

TM715+.3

A

1672-948X(2017)05-0084-06

[责任编辑张 莉]